实训第五天2022/7/15
8:00-9:00 -23
线性回归算法
------------------------------------------------
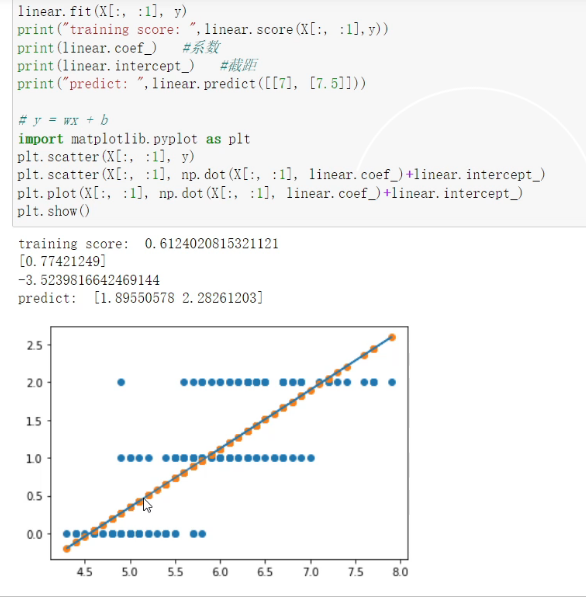
#线性回归
from sklearn import linear_model
linear = linear_model.LinearRegression()
# 训练得到linear模型
linear.fit(X, y) #X四个特征值
# 对训练结果进行评估得分
print("training score: ",linear.score(X, y))
# 显示训练得到的模型参数
# y = wx + b
print(linear.coef_) #系数 4元一次方程
print(linear.intercept_) #截距
# 使用训练出来的linear模型做预测
print("predict: ",linear.predict([[7, 5, 2, 0.5], [7.5, 4, 7, 2]]))
------------------------------------------------
母程序,训练fit出模型linear,用模型预测
w、b首先随机,不断学习,周期不定,到准确
y'=wx+b,y'与y近似时,就停止,确定好w、b
线性回归算法解决分类问题
特征工程:可视化方式、降维方式

10:00-11:00 -24

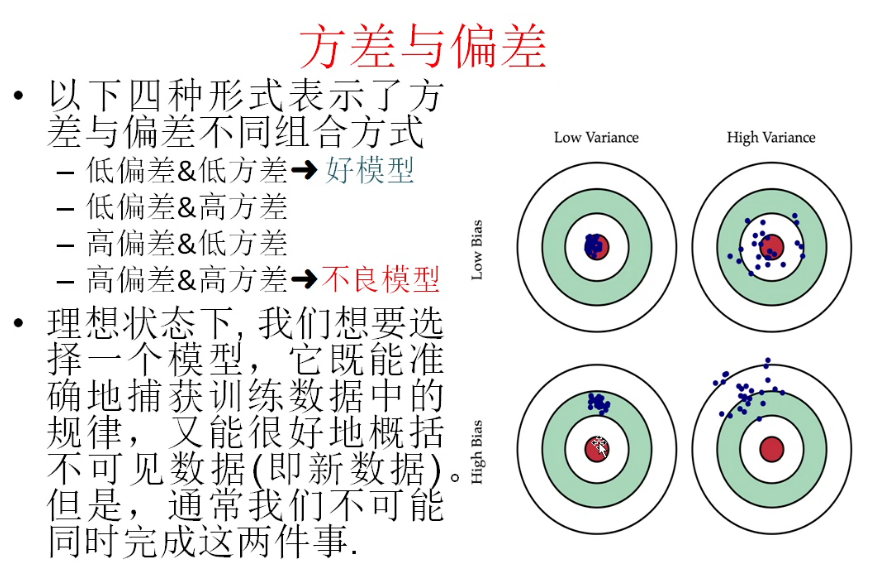
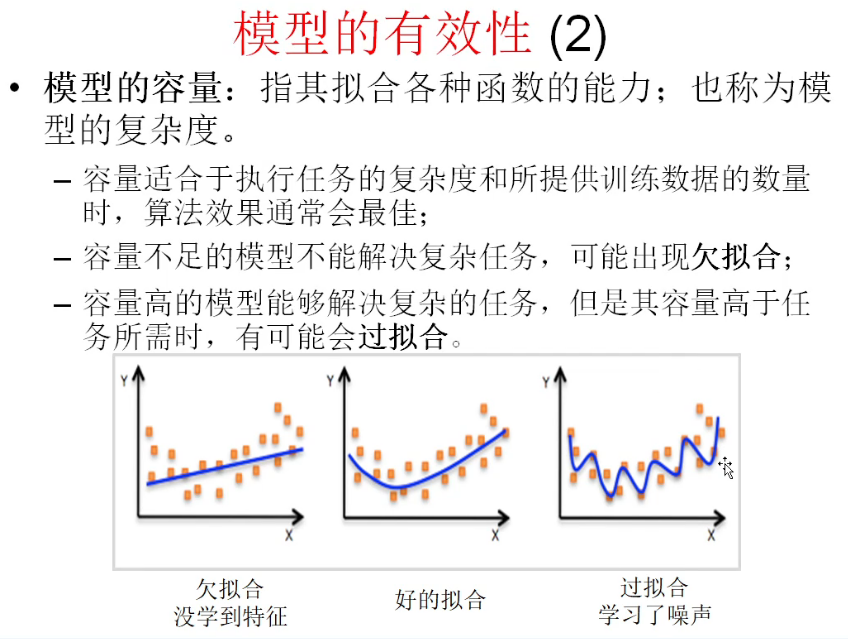
性能指标:均方根误差

11:00-12:00 -25
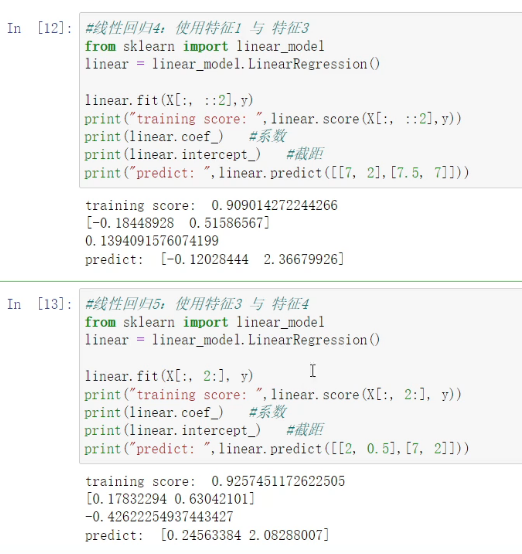
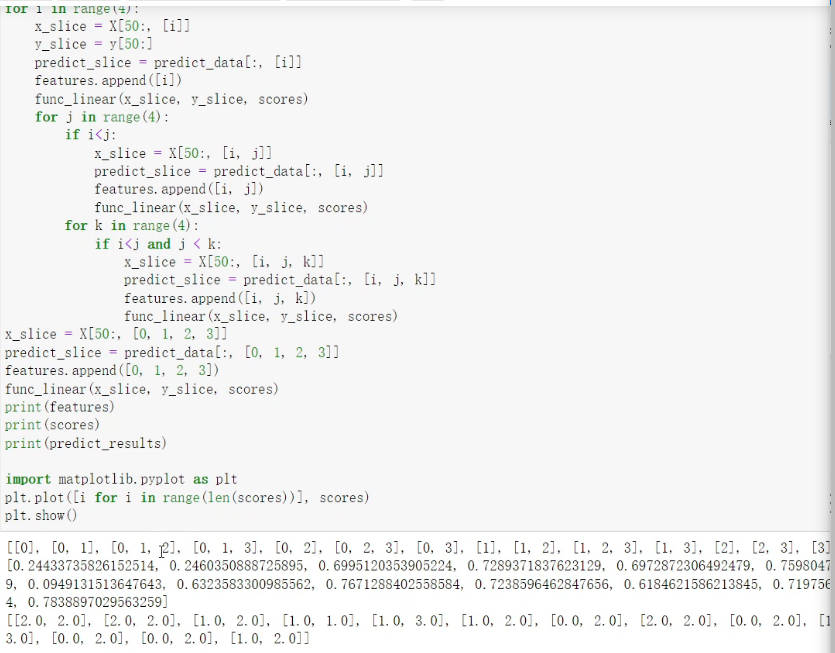
线性回归:特征组合训练
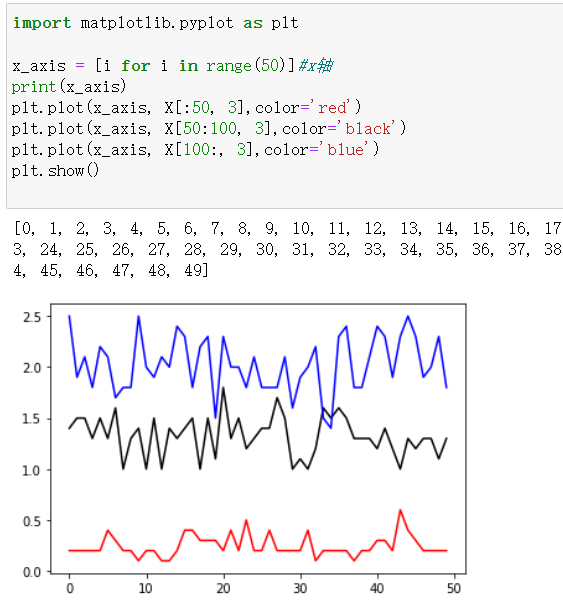
折线图plot()
作业:
逻辑回归:二分类问题的专用方法
支持向量机

14:00-15:00 -26
支持向量机
支持向量:边界数据
分类器
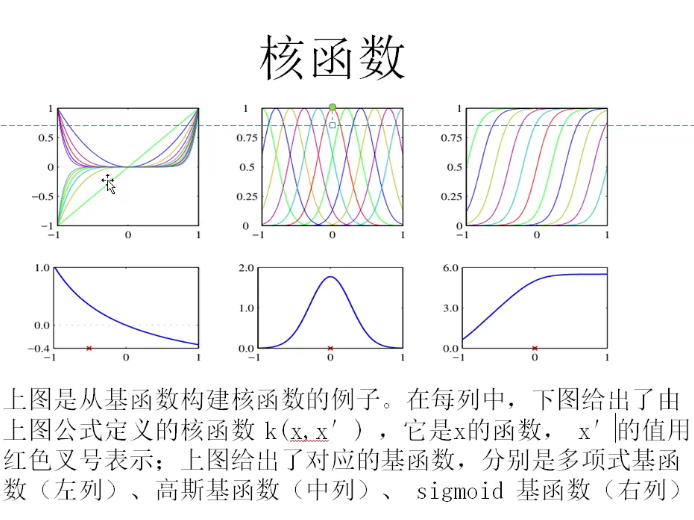
核函数:将数据映射到高维空间
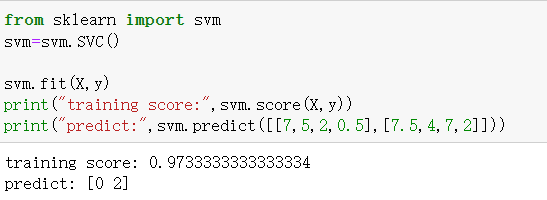

线性核函数
多项式核函数
高斯核函数
sigmoid核函数

径向基函数:

15:00-16:00 -27
线性核函数 kernel='linear'
决策树



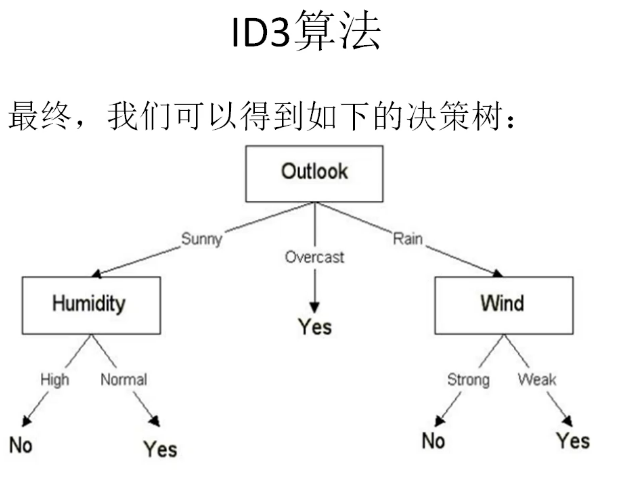
ID3算法

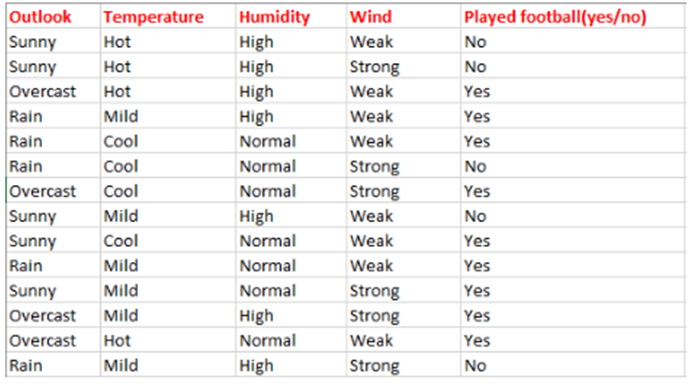
此数据集包含14个样本,类别为二元的,即K = 2。其中正例(类别为1的样本)占的比例为:
P1 = 9/14;反例(类别为0的样本)占的比例为: P2 = 5/14 。
根据信息熵的公式计算出数据集D的信息熵为:
E(S) = -[(9/14)log2(9/14) + (5/14)log2 (5/14)] = 0.94
注意:这里通常将对数的底数设置为2。这里共有14个“yes/no”。
其中有9个是“yes”,5个“no”。在此基础上,计算出了上面的概率。
作业:
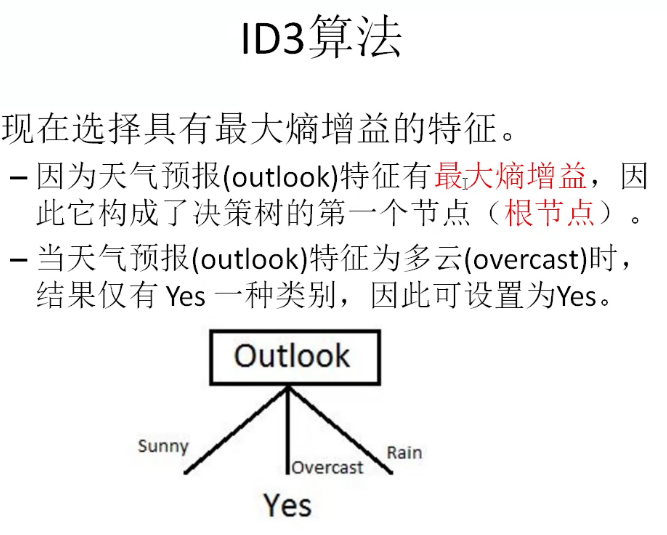
根据上表来计算加权平均熵,即已经计算出的每个特征的权重总和乘以概率。
E(S, outlook) = (5/14)*E(3,2) + (4/14)*E(4,0) + (5/14)*E(2,3)
= (5/14)(-(3/5)log2(3/5)-(2/5)log2(2/5))+ (4/14)(0) + (5/14)((2/5)log2(2/5)-(3/5)log2(3/5))
= 0.693
下一步是计算信息增益,它是上面计算的父节点的熵与加权平均熵之间的差:
IG(S, outlook) = 0.94 - 0.693 = 0.247
同样方式,计算温度(Temperature)、湿度(Humidity)和风力(Wind)的信息增益
IG(S, Temperature) = 0.940 - 0.911 = 0.029
IG(S, Humidity) = 0.940 - 0.788 = 0.152
IG(S, Windy) = 0.940 - 0.8932 = 0.048
温度:hot\mild\cool

16:00-17:00 -28
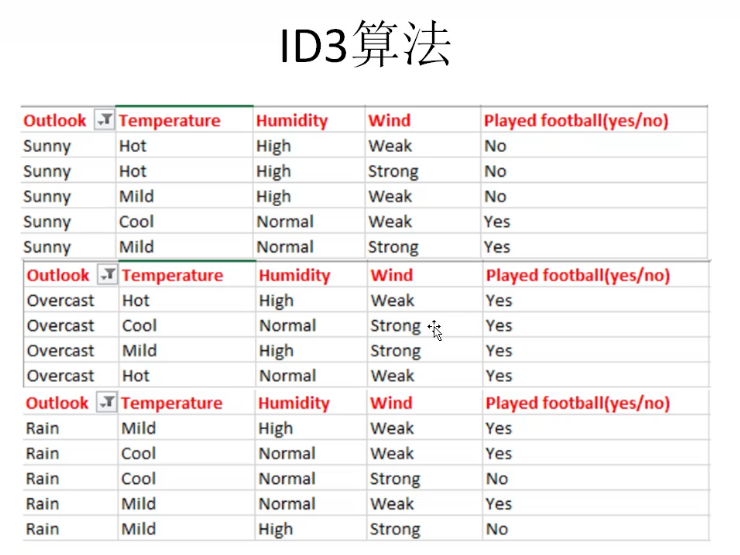
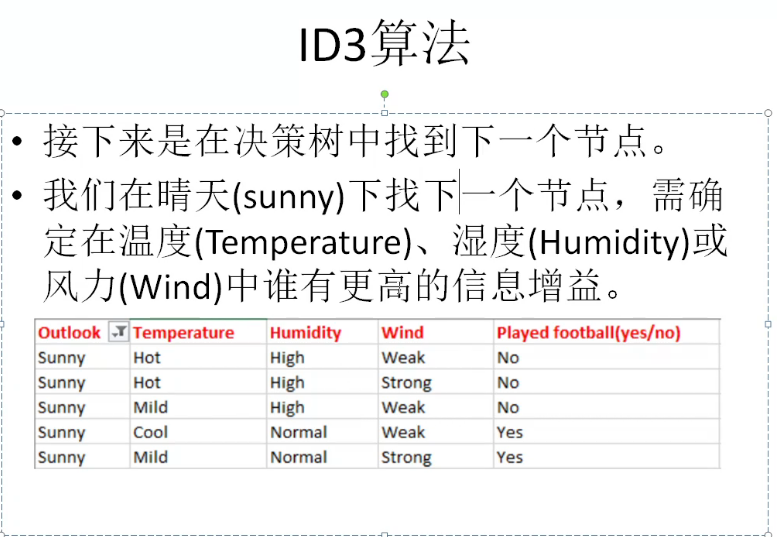








作业:(接上)
使用CART算法分类的过程与ID3算法类似,但是使用基尼不纯度来替代熵作为度量标准。
第一步我们需找到决策树的根节点,为此需计算因变量的基尼不纯度。
Gini(S) = 1 - [(9/14)² + (5/14)²] = 0.4591
下一步,我们将计算基尼增益(Gini Gain)
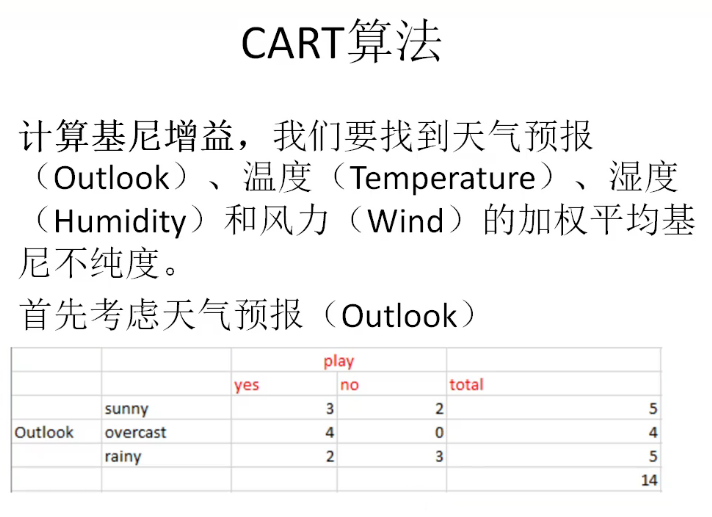
计算基尼增益,我们要找到天气预报(Outlook)、温度(Temperature)、湿度(Humidity)和风力(Wind)的加权平均基尼不纯度。
首先考虑天气预报(Outlook)
首先考虑天气预报(Outlook)
Gini(S, outlook) = (5/14)gini(3,2) + (4/14)*gini(4,0)+ (5/14)*gini(2,3)
= (5/14)(1 - (3/5)² - (2/5)²) + (4/14)*0 + (5/14)(1 - (2/5)² - (3/5)²)
= 0.171+0+0.171 = 0.342
Gini gain(S, outlook) = 0.459 - 0.342 = 0.117
同样地:
Gini gain(S, Temperature) = 0.459 - 0.4405 = 0.0185
Gini gain(S, Humidity) = 0.459 - 0.3674 = 0.0916
Gini gain(S, windy) = 0.459 - 0.4286 = 0.0304
在上面的计算结果中,我们需要选择一个具有最高基尼增益的特征。
从结果来看,天气预报(outlook)的基尼增益为0.117,是最高的,
因此我们选择天气预报(outlook)作为我们的根节点。
接下来的操作,即重复我们在ID3算法中的相同步骤(需要大家给出中间的计算步骤和结果),
只是用基尼增益计算替代信息熵和信息增益计算。
最终,我们可以得到如下的决策树:



