树状数组

　　　　　　　　　　　　　　　　　　　　　　树状数组

 一、引入

　　解题过程中，有时我们需要维护一个前缀和，s[i]=a[1]+a[2]+a[3]+...+a[i] ,容易发现，当我们修改a[i]时,s[i+1],s[i+2]都会随着改变

时间复杂度O(n),因此我们引入树状数组，它的修改和求和都是O（logn）

二、思想及代码实现

A是原始数组，C是树状数组

例如我们要求6的前缀和，只需求c[6]+c[4]即可。

再例如，求7的前缀和，就是 C[7]+C[6]+C[4]

如何实现这个操作呢，我们引入一个函数lowbit，它的作用是求出这个数在2进制下最低位的1，以及他右边的0

例如：6=110(2)，lowbit（6）=10(2)=4。lowbit(4)=4,4-=lowbit(4)=0 结束

7=111(2)，lowbit（7）=1 (2)=1

7-=lowbit(7)=6

lowbit(6)=4

lowbit(4)=4

4-=lowbit(4)=0  结束

严谨证明感兴趣的读者可以自行证明，这里只需记住即可。

int lowbit(int x)
{
    return x&(-x);
}

解释：先将x取反,设x的第k位是1，0--k-1位是0，取反后0--k-1位为1，k位为0，再加上1，x&（~x+1），算出最低位的1根据~n=-1-n，得，~n+1=-n

此外我们还需引入update函数

void update(int x,int y)
{
    while(x<=n)
    {
        c[x]+=y;
        x+=lowbit(x);
    }
}

作用是第x个加上y

求前缀和和sum函数

int sum(int x)
{
    int res=0;
    while(x>0)
    {
        res+=c[x];
        x-=lowbit(x);
    }
    return res;
}

【模板】树状数组 1 

普及/提高-

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  • 将某一个数加上 xx

  • 求出某区间每一个数的和

输入格式

第一行包含两个正整数 n,mn,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 nn 个用空格分隔的整数，其中第 ii 个数字表示数列第 ii 项的初始值。

接下来 mm 行每行包含 33 个整数，表示一个操作，具体如下：

  • 1 x k 含义：将第 xx 个数加上 kk

  • 2 x y 含义：输出区间 [x,y][x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 22 的结果。

输入输出样例

输入 #1 
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出 #1 
14
16

这是一个模板，我们直接看代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int c[1000000],n;
int lowbit(int x)
{
    return x&(-x);
}
int sum(int x)
{
    int res=0;
    while(x>0)
    {
        res+=c[x];
        x-=lowbit(x);
    }
    return res;
}
void update(int x,int y)
{
    while(x<=n)
    {
        c[x]+=y;
        x+=lowbit(x);
    }
}
int main()
{
    int m,a,b,t;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a;
        update(i,a);
    }
    for(int i=1;i<=m;i++)
    {
        cin>>t>>a>>b;
        if(t==1)
        update(a,b);
        else
        cout<<sum(b)-sum(a-1)<<endl;
    }
    return 0;
}

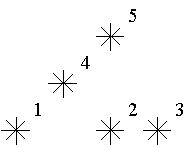
天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。如果一个星星的左下方（包含正左和正下）有i颗星星，就说这颗星星是i级的。

stars1.png

给定星星的位置，输出各级星星的数目。

一句话题意  给定 n个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式

第一行一个整数 ，表示星星的数目；
接下来  行给出每颗星星的坐标，坐标用两个整数  表示；
不会有星星重叠。星星按  坐标增序给出， 坐标相同的按  坐标增序给出。

输出格式

 n行，每行一个整数，分别是  0级， 1级，2 级，……，n-1 级的星星的数目。

样例
输入复制
5
1 1
5 1
7 1
3 3
5 5
输出复制
1
2
1
1
0
比较简单，也是类似模板，直接看代码 
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
using namespace std;
int s[5000000];
int n, m = 32001;
int ans[5000000];
int lowbit(int x) {
    return x & (-x);
}
void update(int x, int v) {
    while (x <= m) {
        s[x] += v;
        x += lowbit(x);
    }
}
int sum(int x) {
    int res = 0;

    while (x > 0) {
        res += s[x];
        x -= lowbit(x);
    }

    return res;
}
int main() {
    int x, y;
    cin >> n;

    for (int i = 1; i <= n; i++) {
        cin >> x >> y;
        x++;
        int v = sum(x);
        update(x, 1);
        ans[v]++;
    }

    for (int i = 0; i < n; i++)
        cout << ans[i] << endl;
}

树状数组2  题目传送门

#include<iostream>
#include<cstdio>
using namespace std;
#define LL long long
LL s[10000000];
LL n,m;
LL lowbit(LL x)
{
    return x&(-x);
}
void update(LL x,LL v)
{
    while(x<=n) {
        s[x]+=v;
        x+=lowbit(x);
    }
}
LL query(int x)
{
    LL res=0;
    while(x>0)
    {
        res+=s[x];
        x-=lowbit(x);
    }
    return res;
}
int main()
{
    LL x,y,k,now=0;
    cin>>n>>m;
    for(LL i=1;i<=n;i++)
    {
        cin>>x;
        update(i,x-now);  //差分
        now=x;
    }
    while(m--)
    {
        cin>>k;
        if(k==1)
        {
            cin>>x>>y>>k;
            update(x,k);
            update(y+1,-k);
        }
        else 
        {
            cin>>x;
            cout<<query(x)<<endl;
        }
    }
}

总结一下：树状数组在数据结构方面与线段树具有异曲同工之处，能用树状数组做的，基本上线段树都能搞定，

　　　　但树状数组时间复杂度更低，并且可以大幅度降低调试难度。

posted @ 2021-03-20 15:34  S_Curry  阅读(34)  评论(0)  编辑  收藏  举报