数论
数论
第一章:整除理论
(2)整除的基本知识
定义1:
设 a,b ∈ Z , a ≠ 0,如果存在 q ∈ Z , 使得 b=aq,那么就说 b 可被 a 整除,记作 b | a,且称 b 是 a 的倍数,
a 是 b 的约数。
定理1:
a | b <=> -a | b <=> a | -b <=> |a| | |b|。
(3)带余数除法
定理1:
设 a,b 是两个给定的整数,a ≠ 0,那么一定存在唯一的一对整数 q 与 r,满足
b = aq + r,0 ≤ r < |a|。
定理2:
设 a,b 是两个给定的整数,a ≠ 0,再设 d 是一给定的整数,那么一定存在唯一的一对整数 q 与 r,满足
b = aq + r,d ≤ r < |a|+d。
(4)最大公约数理论
定理5:
设 GCD(m,a) = 1,则有 GCD(m,ab) = GCD(m,b),这就是说“求 m 与另一个数的最大公约数时,可以把另一个数中与 m 互素的因数去掉”。
定理6:
设 GCD(m,a) = 1,那么若 m | ab,则 m | b,这就是说“若一个数被 m 整除,则把这个数中与 m 互素的因数去掉后仍被 m 整除”。
定理7:
LCM[ a,b ] × GCD(a,b) = |ab|。
定理8:
GCD(a,b) = GCD(a,b-a) = GCD(b,b-a)。
相关习题:戳这里👉
(5)最大公约数与最小公倍数
(a,b) = a 与 b 的最大公约数。
[a,b] = a 与 b 的最小公倍数。
定理1:
GCD(a,b) = GCD(-a,b) = GCD(a,-b) = GCD( |a| , |b| )。
定理2:
LCM[a,b] = LCM[-a,b] = LCM[a,-b] = LCM[ |a| , |b| ]。
第三章:同余的基本知识
(1)同余的定义及基本性质
定义1:
设 m ≠ 0,若 m | a-b,即 a-b = km,则称 m 为模,a 同余于 b 模 m ,b 是 a 对模 m 的剩余,记作
a ≡ b (mod m);
因为 m | a-b = (-m) | a-b,所以以后总假设 m ≥ 1。
性质1:
· a+c ≡ b+c (mod m);
· a-c ≡ b-c (mod m);
· a*c ≡ b*c (mod m);
性质2:
如果 ac ≡ bc (mod m) 那么 a ≡ b (mod m div GCD(m,c) )。
证明如下:

由同余定理,模运算规则如下:
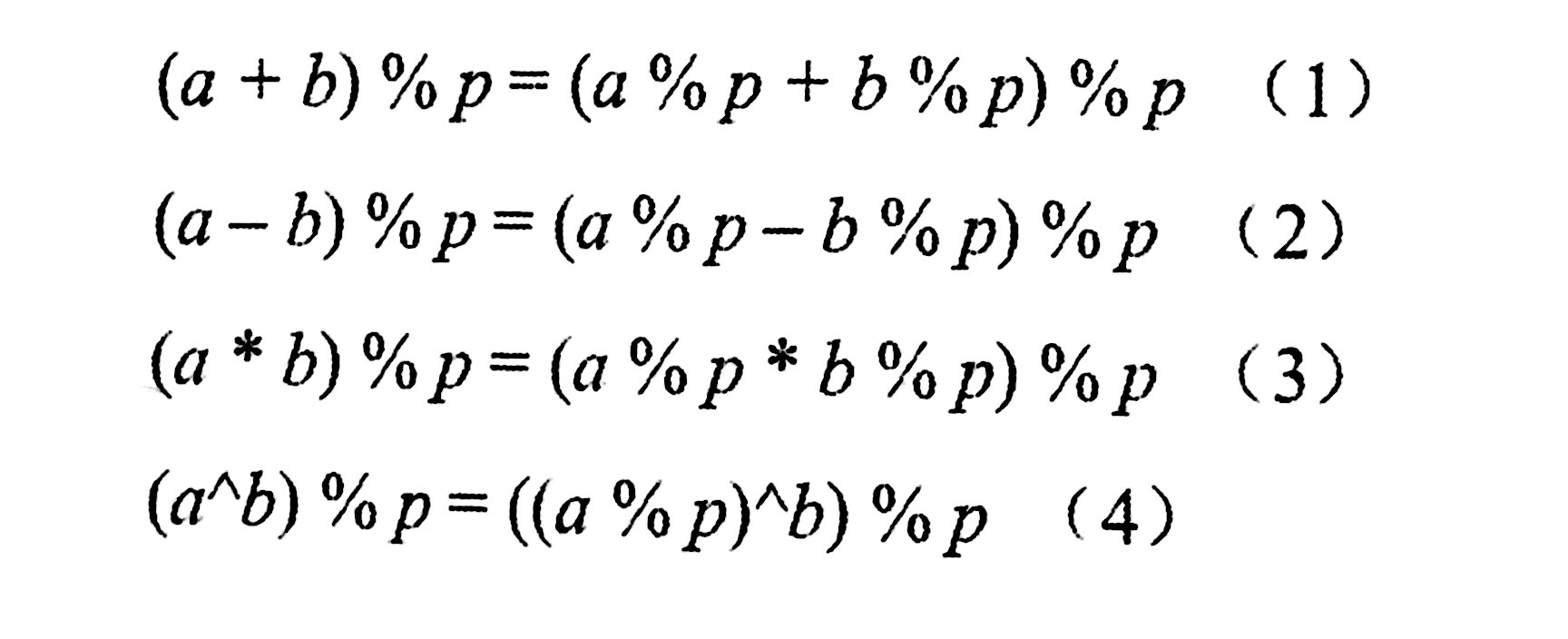

(2)同余类与剩余系
定义1(同余类或剩余类):
把全体整数分成这样的若干个两两不相交的集合,使得在同一个集合中的任意两个数对模m 一定同余;
而属于不同集合中的两个数对模m一定不同余;
每一个这样的集合称为模m的同余类或模m的剩余类;
例如:模3的同余类有
{0,3,6,...,3*k},{1,4,7,....,3*k+1},{2,5,8,.....3*k+2}
我们以 r mod m 表示 r 所属的模m的同余类;
例如上例,如果 r = 0,那么 r 所属的模m的同余类为{0,3,6,...,3*k};
定义2(完全剩余系):
一组数 y1,y2,.....ym 称为模 m 的完全剩余系,当且仅当对任意的整数 a 有且仅有一个 yj 使得同余式a ≡ yj (mod m)成立。
简言之,对于任意 i,j ∈ [1,m],且 i ≠ j,有 m%yi ≠ m%yj。
从模m的每个同余类中各挑一个元素组成的集合就是模m的完全剩余系。
{0,1,2,.....,m-1}是最简单的一个模m的完全剩余系;
定义3(既约(或互素)同(剩)余类):
在模m的同余类 r mod m 中,如果GCD(r,m) == 1,就称 r mod m 为模m的既约同余类;
模m的所有既约同余类的个数记作φ(m),通常称为Euler函数。
定义4(既约(互素)剩余系):
模 m 的既约剩余系是 m 的完全剩余系中与 m 互素的数构成的子集;
易得,模 m 的既约剩余系中的元素的个数为 φ(m)。
例如, m = 10,m的一个完全剩余系为{0,1,2,......,9},其中与10互素的数组成的集合为 { 1,3,7,9 } ,并且任何两个元素模 10 不同余,;
{ 1,3,7,9 } 就为模 m 的一个既约剩余系,φ(10) = 4。
定理4:
设 m1 | m,那么对任意 r 有
r mod m ⊆ r mod m1;
 定理4证明
定理4证明
定理4':
设 m1 | m,那么对任意 r,同余式 n ≡ r(mod m1) 成立的充要条件是以下 d=m/m1 个同余式
n ≡ r + j*m1(mod m);( j∈[0,d-1])
有且仅有一个成立。
 定理4'证明
定理4'证明
定理6:
模m的所有不同的既约同余类是
r mod m , GCD(r,m) = 1, 1≤ r ≤ m;
φ(m)=1,2,...,m 中和m既约的数的个数。
定理7:
(1)在任意取定的 φ(m)+1 个均和 m 既约的整数中,必有两个数对模m同余。
(2)存在φ(m)个数两两对模m不同余且均和m既约。
(3)Euler函数φ(m)的求解
定理1:如果 k 为素数,那么 φ(k) = k-1




