树

　　　　　　　　　　　　　　　　　　　　　　树

---

 

树是一种数据结构，它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树。

 

二叉树

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分 [1]  。

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个结点

 

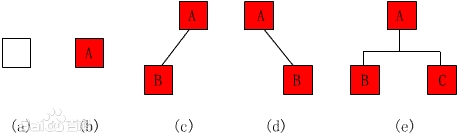
五种基本形态

 

 

相关术语

编辑

①结点：包含一个数据元素及若干指向子树分支的信息

②结点的度：一个结点拥有子树的数目称为结点的度

③叶子结点：也称为终端结点，没有子树的结点或者度为零的结点 

④分支结点：也称为非终端结点，度不为零的结点称为非终端结点

⑤树的度：树中所有结点的度的最大值 

⑥结点的层次：从根结点开始，假设根结点为第1层，根结点的子节点为第2层，依此类推，如果某一个结点位于第L层，则其子节点位于第L+1层 

⑦树的深度：也称为树的高度，树中所有结点的层次最大值称为树的深度 

⑧有序树：如果树中各棵子树的次序是有先后次序，则称该树为有序树 

⑨无序树：如果树中各棵子树的次序没有先后次序，则称该树为无序树 

⑩森林：由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根结点删除，则该树就变成了一片森林，森林中的树由原来根结点的各棵子树构成 

二叉树性质

编辑

性质1：二叉树的第i层上至多有2i-1（i≥1）个节点 

性质2：深度为h的二叉树中至多含有2h-1个节点 

性质3：若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1 

性质4：具有n个节点的完全二叉树深为log2x+1（其中x表示不大于n的最大整数） 

性质5：若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点： 

当i=1时，该节点为根，它无双亲节点 。

当i>1时，该节点的双亲节点的编号为i/2 

若2i≤n，则有编号为2i的左节点，否则没有左节点 

若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点 

 

二叉树的遍历方式

．先（根）序遍历的递归算法定义：

若二叉树非空，则依次执行如下操作：

⑴ 访问根结点；

⑵ 遍历左子树；

⑶ 遍历右子树。

2．中（根）序遍历的递归算法定义：

若二叉树非空，则依次执行如下操作：

⑴遍历左子树；

⑵访问根结点；

⑶遍历右子树。

3．后（根）序遍历得递归算法定义：

若二叉树非空，则依次执行如下操作：

⑴遍历左子树；

⑵遍历右子树；

⑶访问根结点。

 

树(7张)

树（tree）是包含

个结点，

条边的有穷集，其中：

（1）每个元素称为结点（node）。

（2）有一个特定的结点被称为根结点或树根（root）。

（3）除根结点之外的其余数据元素被分为

个互不相交的集合

，其中每一个集合

本身也是一棵树，被称作原树的子树（subtree）。

树也可以这样定义：树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或称为树根。

我们可以形式地给出树的递归定义如下:

单个结点是一棵树，树根就是该结点本身。

设

是树，它们的根结点分别为

。用一个新结点

作为

的父亲，则得到一棵新树，结点n就是新树的根。我们称

为一组兄弟结点，它们都是结点

的子结点。我们还称

为结点n的子树。

空集合也是树，称为空树。空树中没有结点；

孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；

结点的度：一个结点含有的子结点的个数称为该结点的度；

叶结点或终端结点：度为0的结点称为叶结点；

非终端结点或分支结点：度不为0的结点；

双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；

兄弟结点：具有相同父结点的结点互称为兄弟结点；

树的度：一棵树中，最大的结点的度称为树的度；

结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；

树的高度或深度：树中结点的最大层次；

堂兄弟结点：双亲在同一层的结点互为堂兄弟；

结点的祖先：从根到该结点所经分支上的所有结点；

子孙：以某结点为根的子树中任一结点都称为该结点的子孙；

森林：由

棵互不相交的树的集合称为森林。

种类

编辑

无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树；

有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；

二叉树：每个节点最多含有两个子树的树称为二叉树；

满二叉树：叶节点除外的所有节点均含有两个子树的树被称为满二叉树；

完全二叉树：有

个节点的满二叉树称为完全二叉树；

哈夫曼树（最优二叉树）：带权路径最短的二叉树称为哈夫曼树或最优二叉树。

深度

编辑

定义一棵树的根结点层次为1，其他结点的层次是其父结点层次加1。一棵树中所有结点的层次的最大值称为这棵树的深度。

表示方法

编辑

图像表达法

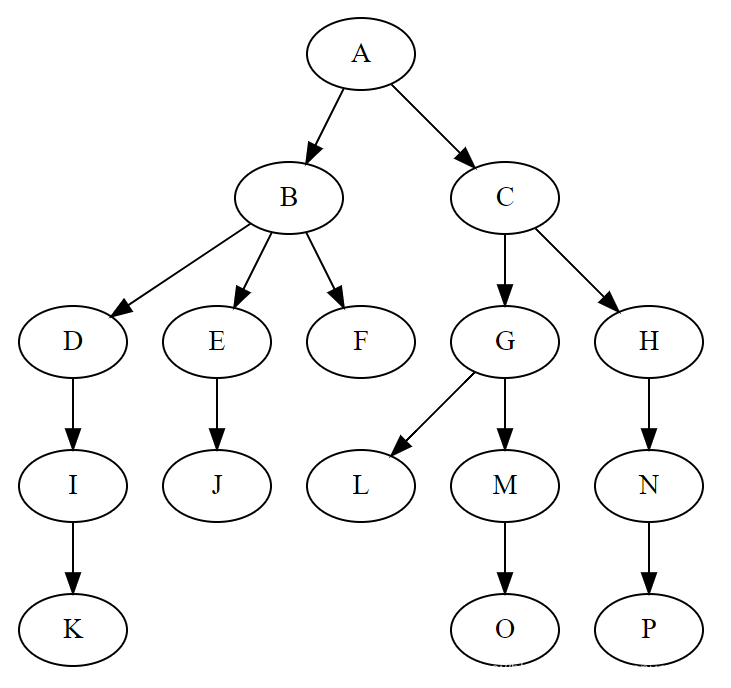
树的表示方法有很多种，最常用的是图像表示法。

以下是一个普通的树（非二叉树）：

符号表达法

用括号先将根结点放入一对圆括号中，然后把它的子树由左至右的顺序放入括号中，而对子树也采用同样的方法处理；同层子树与它的根结点用圆括号括起来，同层子树之间用逗号隔开，最后用闭括号括起来。如前文树形表示法可以表示为：

遍历表达法

遍历表达法有4种方法：先序遍历、中序遍历、后序遍历、层次遍历

例如右图：

其先序遍历（又称先根遍历）为ABDECF（根-左-右）

其中序遍历（又称中根遍历）为DBEAFC（左-根-右）（仅二叉树有中序遍历）

其后序遍历（又称后根遍历）为DEBFCA（左-右-根）

其层次遍历为ABCDEF（同广度优先搜索
）