2014 ACM/ICPC Asia Regional Shanghai Online【未完成】
1012
the Sum of Cube
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2407 Accepted Submission(s): 936
Problem Description
A range is given, the begin and the end are both integers. You should sum the cube of all the integers in the range.
Input
The first line of the input is T(1 <= T <= 1000), which stands for the number of test cases you need to solve.
Each case of input is a pair of integer A,B(0 < A <= B <= 10000),representing the range[A,B].
Each case of input is a pair of integer A,B(0 < A <= B <= 10000),representing the range[A,B].
Output
For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then output the answer – sum the cube of all the integers in the range.
Sample Input
2
1 3
2 5
Sample Output
Case #1: 36 Case #2: 224
这个大水题居然wa一次
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 6 const int maxn = 105; 7 8 int main() { 9 int t; 10 scanf("%d",&t); 11 for(int kase = 1; kase <= t; kase++) { 12 int a, b; 13 scanf("%d %d",&a, &b); 14 long long sum = 0; 15 for(int i = a; i <= b; i++) { 16 sum += i * i * i; 17 } 18 printf("Case #%d: %I64d\n", kase, sum); 19 } 20 return 0; 21 }
wa的原因是对强制类型转换的不熟悉, 对于第16行i*i*i仍然是个int型但是不能自动转换为long long
所以只要加一个强转就可以了-。-
代码:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 6 const int maxn = 1005; 7 8 int main() { 9 int t; 10 int a, b; 11 scanf("%d",&t); 12 for(int kase = 1; kase <= t; kase++) { 13 scanf("%d %d",&a, &b); 14 long long sum = 0; 15 for(int i = a; i <= b; i++) { 16 sum += (long long ) i * i * i; 17 } 18 printf("Case #%d: %I64d\n", kase, sum); 19 } 20 return 0; 21 }
1009
Divided Land
Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1950 Accepted Submission(s): 659
Problem Description
It’s time to fight the local despots and redistribute the land. There is a rectangular piece of land granted from the government, whose length and width are both in binary form. As the mayor, you must segment the land into multiple squares of equal size for the villagers. What are required is there must be no any waste and each single segmented square land has as large area as possible. The width of the segmented square land is also binary.
Input
The first line of the input is T (1 ≤ T ≤ 100), which stands for the number of test cases you need to solve
Each case contains two binary number represents the length L and the width W of given land. (0 < L, W ≤ 21000)
Each case contains two binary number represents the length L and the width W of given land. (0 < L, W ≤ 21000)
Output
For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then one number means the largest width of land that can be divided from input data. And it will be show in binary. Do not have any useless number or space.
Sample Input
3
10 100
100 110
10010 1100
Sample Output
Case #1: 10
Case #2: 10
Case #3: 110
大意:二进制求其gcd并且用二进制表示出来
21000
有点大直接用java大数
这里有一些java大数的常用函数:

1 在用C或者C++处理大数时感觉非常麻烦,但是在JAVA中有两个类BigInteger和BigDecimal分别表示大整数类和大浮点数类,至于两个类的对象能表示最大范围不清楚,理论上能够表示无线大的数,只要计算机内存足够大。 2 这两个类都在java.math.*包中,因此每次必须在开头处引用该包。 3 4 Ⅰ基本函数: 5 1.valueOf(parament); 将参数转换为制定的类型 6 比如 int a=3; 7 BigInteger b=BigInteger.valueOf(a); 8 则b=3; 9 String s=”12345”; 10 BigInteger c=BigInteger.valueOf(s); 11 则c=12345; 12 13 2.add(); 大整数相加 14 BigInteger a=new BigInteger(“23”); 15 BigInteger b=new BigInteger(“34”); 16 a. add(b); 17 18 3.subtract(); 相减 19 4.multiply(); 相乘 20 5.divide(); 相除取整 21 6.remainder(); 取余 22 7.pow(); a.pow(b)=a^b 23 8.gcd(); 最大公约数 24 9.abs(); 绝对值 25 10.negate(); 取反数 26 11.mod(); a.mod(b)=a%b=a.remainder(b); 27 12.max(); min(); 28 13.punlic int comareTo(); 29 14.boolean equals(); 是否相等 30 15.BigInteger构造函数: 31 一般用到以下两种: 32 BigInteger(String val); 33 将指定字符串转换为十进制表示形式; 34 BigInteger(String val,int radix); 35 将指定基数的 BigInteger 的字符串表示形式转换为 BigInteger 36 Ⅱ.基本常量: 37 A=BigInteger.ONE 1 38 B=BigInteger.TEN 10 39 C=BigInteger.ZERO 0 40 Ⅲ.基本操作 41 1. 读入: 42 用Scanner类定义对象进行控制台读入,Scanner类在java.util.*包中 43 Scanner cin=new Scanner(System.in);// 读入 44 while(cin.hasNext()) //等同于!=EOF 45 { 46 int n; 47 BigInteger m; 48 n=cin.nextInt(); //读入一个int; 49 m=cin.BigInteger();//读入一个BigInteger; 50 System.out.print(m.toString()); 51 } 52 Ⅳ.运用 53 四则预算: 54 import java.util.Scanner; 55 import java.math.*; 56 import java.text.*; 57 public class Main 58 { 59 public static void main(String args[]) 60 { 61 Scanner cin = new Scanner ( System.in ); 62 BigInteger a,b; 63 int c; 64 char op; 65 String s; 66 while( cin.hasNext() ) 67 { 68 a = cin.nextBigInteger(); 69 s = cin.next(); 70 op = s.charAt(0); 71 if( op == '+') 72 { 73 b = cin.nextBigInteger(); 74 System.out.println(a.add(b)); 75 } 76 else if( op == '-') 77 { 78 b = cin.nextBigInteger(); 79 System.out.println(a.subtract(b)); 80 } 81 else if( op == '*') 82 { 83 b = cin.nextBigInteger(); 84 System.out.println(a.multiply(b)); 85 } 86 else 87 { 88 BigDecimal a1,b1,eps; 89 String s1,s2,temp; 90 s1 = a.toString(); 91 a1 = new BigDecimal(s1); 92 b = cin.nextBigInteger(); 93 s2 = b.toString(); 94 b1 = new BigDecimal(s2); 95 c = cin.nextInt(); 96 eps = a1.divide(b1,c,4); 97 //System.out.println(a + " " + b + " " + c); 98 //System.out.println(a1.doubleValue() + " " + b1.doubleValue() + " " + c); 99 System.out.print( a.divide(b) + " " + a.mod(b) + " "); 100 if( c != 0) 101 { 102 temp = "0."; 103 for(int i = 0; i < c; i ++) temp += "0"; 104 DecimalFormat gd = new DecimalFormat(temp); 105 System.out.println(gd.format(eps)); 106 } 107 else System.out.println(eps); 108 } 109 } 110 } 111 } 112 //===================================================================================== 113 //PKU1311八进制浮点数化为十进制浮点数,高精度 114 import java.io.*; 115 import java.util.*; 116 import java.math.*; 117 public class Main 118 { 119 public static void main(String[] args) 120 { 121 Scanner cin=new Scanner(System.in); 122 BigDecimal temp,sum,ans,num; //java大数 123 String str; 124 int i,len; 125 while(cin.hasNext()) 126 { 127 str=cin.next(); 128 len=str.length(); 129 temp=BigDecimal.valueOf(8.0); 130 sum=BigDecimal.ONE; 131 ans=BigDecimal.ZERO; 132 for(i=2;i<len;i++) 133 { 134 int val=str.charAt(i)-'0'; 135 num=BigDecimal.valueOf(val); 136 sum=sum.multiply(temp); //8的n次幂 137 ans=ans.add(num.divide(sum)); //按权累加 138 } 139 System.out.printf("%s [8] = ",str); 140 System.out.println(ans+" [10]"); 141 } 142 } 143 }
代码:

1 import java.io.*; 2 import java.util.*; 3 import java.math.*; 4 5 public class b { 6 public static void main(String[] args) { 7 Scanner cin = new Scanner(System.in); 8 9 int t = cin.nextInt(); 10 11 for(int kase = 1; kase <= t; kase++) { 12 String s1, s2; 13 14 BigInteger On = BigInteger.ONE; 15 BigInteger Ze = BigInteger.ZERO; 16 BigInteger Tw = BigInteger.valueOf(2); 17 18 BigInteger sum1 = Ze; 19 BigInteger sum2 = Ze; 20 BigInteger t1 = On; 21 BigInteger t2 = On; 22 23 s1 = cin.next(); s2 = cin.next(); 24 int l1 = s1.length(); int l2 = s2.length(); 25 for(int i = l1 - 1; i >= 0; i--) { 26 if(s1.charAt(i) == '1') { 27 sum1 = sum1.add(t1); 28 } 29 t1 = t1.multiply(Tw); 30 } 31 for(int i = l2 - 1; i >= 0; i--) { 32 if(s2.charAt(i) == '1') { 33 sum2 = sum2.add(t2); 34 } 35 t2 = t2.multiply(Tw); 36 } 37 sum1 = sum1.gcd(sum2); 38 int [] ans = new int [1005]; 39 int cnt = 0; 40 while(!sum1.equals(Ze)) { 41 if(sum1.mod(Tw).equals(On)) { 42 ans[cnt++] = 1; 43 } else ans[cnt++] = 0; 44 sum1 = sum1.divide(Tw); 45 } 46 System.out.print("Case #" + kase + ": "); 47 for(int i = cnt - 1; i >= 0; i--) { 48 System.out.print(ans[i]); 49 } 50 System.out.println(""); 51 } 52 } 53 }
1004
Contest
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1705 Accepted Submission(s): 446
Problem Description
In the ACM International Collegiate Programming Contest, each team consist of three students. And the teams are given 5 hours to solve between 8 and 12 programming problems.
On Mars, there is programming contest, too. Each team consist of N students. The teams are given M hours to solve M programming problems. Each team can use only one computer, but they can’t cooperate to solve a problem. At the beginning of the ith hour, they will get the ith programming problem. They must choose a student to solve this problem and others go out to have a rest. The chosen student will spend an hour time to program this problem. At the end of this hour, he must submit his program. This program is then run on test data and can’t modify any more.
Now, you have to help a team to find a strategy to maximize the expected number of correctly solved problems.
For each problem, each student has a certain probability that correct solve. If the ith student solve the jth problem, the probability of correct solve is Pij .
At any time, the different between any two students’ programming time is not more than 1 hour. For example, if there are 3 students and there are 5 problems. The strategy {1,2,3,1,2}, {1,3,2,2,3} or {2,1,3,3,1} are all legal. But {1,1,3,2,3},{3,1,3,1,2} and {1,2,3,1,1} are all illegal.
You should find a strategy to maximize the expected number of correctly solved problems, if you have know all probability
On Mars, there is programming contest, too. Each team consist of N students. The teams are given M hours to solve M programming problems. Each team can use only one computer, but they can’t cooperate to solve a problem. At the beginning of the ith hour, they will get the ith programming problem. They must choose a student to solve this problem and others go out to have a rest. The chosen student will spend an hour time to program this problem. At the end of this hour, he must submit his program. This program is then run on test data and can’t modify any more.
Now, you have to help a team to find a strategy to maximize the expected number of correctly solved problems.
For each problem, each student has a certain probability that correct solve. If the ith student solve the jth problem, the probability of correct solve is Pij .
At any time, the different between any two students’ programming time is not more than 1 hour. For example, if there are 3 students and there are 5 problems. The strategy {1,2,3,1,2}, {1,3,2,2,3} or {2,1,3,3,1} are all legal. But {1,1,3,2,3},{3,1,3,1,2} and {1,2,3,1,1} are all illegal.
You should find a strategy to maximize the expected number of correctly solved problems, if you have know all probability
Input
The first line of the input is T (1 ≤ T ≤ 20), which stands for the number of test cases you need to solve.
The first line of each case contains two integers N ,M (1 ≤ N ≤ 10,1 ≤ M ≤ 1000),denoting the number of students and programming problem, respectively
The next N lines, each lines contains M real numbers between 0 and 1 , the jth number in the ith line is Pij .
The first line of each case contains two integers N ,M (1 ≤ N ≤ 10,1 ≤ M ≤ 1000),denoting the number of students and programming problem, respectively
The next N lines, each lines contains M real numbers between 0 and 1 , the jth number in the ith line is Pij .
Output
For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then a single real number means the maximal expected number of correctly solved problems if this team follow the best strategy, to five digits after the decimal point. Look at the output for sample input for details.
Sample Input
1
2 3
0.6 0.3 0.4
0.3 0.7 0.9
Sample Output
Case #1: 2.20000
分析:数位dp
代码:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 6 const int maxn = 1005; 7 8 double dp[1005][1<<11]; 9 double p[15][1<<11]; 10 11 int main() { 12 int t; 13 int n, m; 14 scanf("%d", &t); 15 for(int kase = 1; kase <= t; kase ++) { 16 scanf("%d %d", &n, &m); 17 for(int i = 0; i < n; i++) { 18 for(int j = 0; j < m; j++) { 19 scanf("%lf", &p[i][j]); 20 } 21 } 22 int maxa = 1 << n; 23 for(int i = 0; i < m; i++) { 24 for(int j = 0; j < maxa; j++) { 25 dp[i][j] = -1.0; 26 } 27 } 28 for(int i = 0; i < n; i++) { 29 dp[0][1 << i] = p[i][0]; 30 } 31 for(int i = 1; i < m; i++) { 32 for(int j = 0; j < maxa; j++) { 33 if(dp[i - 1][j] != -1) { 34 for(int k = 0; k < n; k++) { 35 if((j & ( 1 << k ) ) == 0 ) { 36 dp[i][j | ( 1 << k ) ] = max ( dp[i][j | ( 1 << k )], dp[i - 1][j] + p[k][i]); 37 } 38 } 39 } 40 } 41 if(dp[i][maxa - 1] != -1) { 42 dp[i][0] = dp[i][maxa - 1]; 43 } 44 dp[i][maxa - 1] = -1; 45 } 46 double ans = 0; 47 for(int i = 0; i < maxa; i++) { 48 ans = max(ans, dp[m - 1][i]); 49 } 50 printf("Case #%d: %.5lf\n", kase, ans); 51 } 52 return 0; 53 }
Sawtooth
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2979 Accepted Submission(s): 450
Problem Description
Think about a plane:
● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...
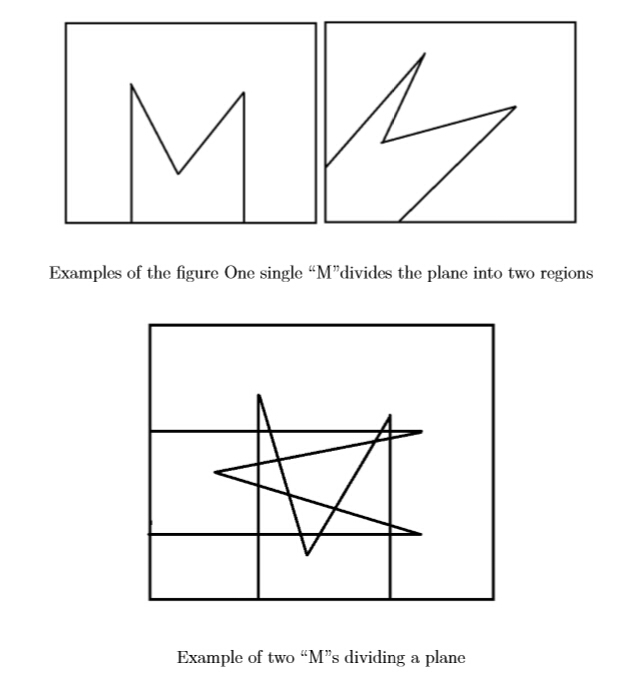
Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?
● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...
Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?

Input
The first line of the input is T (1 ≤ T ≤ 100000), which stands for the number of test cases you need to solve
Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 1012)
Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 1012)
Output
For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then an integer that is the maximum number of regions N the “M” figures can divide.
Sample Input
2
1
2
Sample Output
Case #1: 2
Case #2: 19
题意:如图所示一个‘M’最多把一个平面分成两个部分,两个平面是19个
问给你n个平面最多能的分成多少个n的数量级是10^12
分析:
这个题的思路跟这个题是一样的
我们先考虑这么一道题:n条直线最多能够把一个平面分成几个平面

我们知道对于第n条直线最多与n-1条直线相交,也就是最多有n-1个焦点
我们还知道对于每增加x一个焦点那么增加的平面个数x+1
也就是说对于第n条直线增了n个平面
a1 = 2;a2 = 2 + 2 = 4;
an = a1 + sum(2……n) = 2 + ((1+n) * n / 2 - 1) = n*(n+1)/2 + 1;
那么对于n对2条平行的直线呢

同样的
对于第n(n代表第n对)对直线 增加的焦点个数 为 2 * ( 2 * ( n - 1 ) )
同理可以获得增加的平面个数 对于单条直线每增加x个焦点增加x+1个平面
那么对于平行的两条直线每增加 增加的焦点个数为 2 * ( 2 * ( n - 1) + 1 ) 个平面 我们将它设为x
那么an = a1 + sum(xi)【i = 2……n】
现在我们在考虑这么一个问题
如果不是平行的两条直线,而是v字形的呢像这样

我们发现对于一对平行线每增加一个焦点平面个数就减一
那么n对平行线就是总平面个数减去n即可
到这里思路已经全部说完了
“M"就是四条平行线s个焦点
只要求出平行线的平面数再减去3n就可以了
最终的的公式为 an = 8*n*n - 7 * n + 1
但是作者卡java的大数……*&……(*&%*&%&……&%*&(*)&(**&%&%&……%¥……*&……*%……&¥%……¥……%#¥#%……¥
其实很好考虑的longlong的最大值9223372036854775807 也就说9*10^17只内就能承受
于是我们这么考虑
对于两个数相乘
形式如ab*cd
那么
a b
* c d
--------------
= ad bd
ac bc
----------------
= ac(ad+bc)bd
所以我们可以把10^12分成两个部分分别计算每个部分10^7
最后合并起来不够的用零填充%07I64d %07lld
代码:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstdio> 4 using namespace std; 5 6 typedef long long LL; 7 const int mod = 10000000; 8 9 int main() { 10 LL a, b, a1, a2, b1, b2, n, ans1, ans2, ans3; 11 int t; 12 scanf("%d",&t); 13 for(int kase = 1; kase <= t; kase++) { 14 scanf("%I64d", &n); 15 a = n; b = n * 8 - 7; 16 a1 = a / mod; a2 = a % mod; 17 b1 = b / mod; b2 = b % mod; 18 ans1 = 0; ans2 = 0; ans3 = 0; 19 ans3 = a2 * b2 + 1; ans2 = a1 * b2 + a2 * b1; ans1 = a1 * b1; 20 ans2 += ans3 / mod; ans3 %= mod; 21 ans1 += ans2 / mod; ans2 %= mod; 22 printf("Case #%d: ", kase); 23 if(ans1) { 24 printf("%I64d%07I64d%07I64d\n", ans1, ans2, ans3); 25 } else if(ans2) { 26 printf("%I64d%07I64d\n", ans2, ans3); 27 } else { 28 printf("%I64d\n",ans3); 29 } 30 31 } 32 return 0; 33 }






