树、二叉树、查找算法总结
思维导图
重要概念
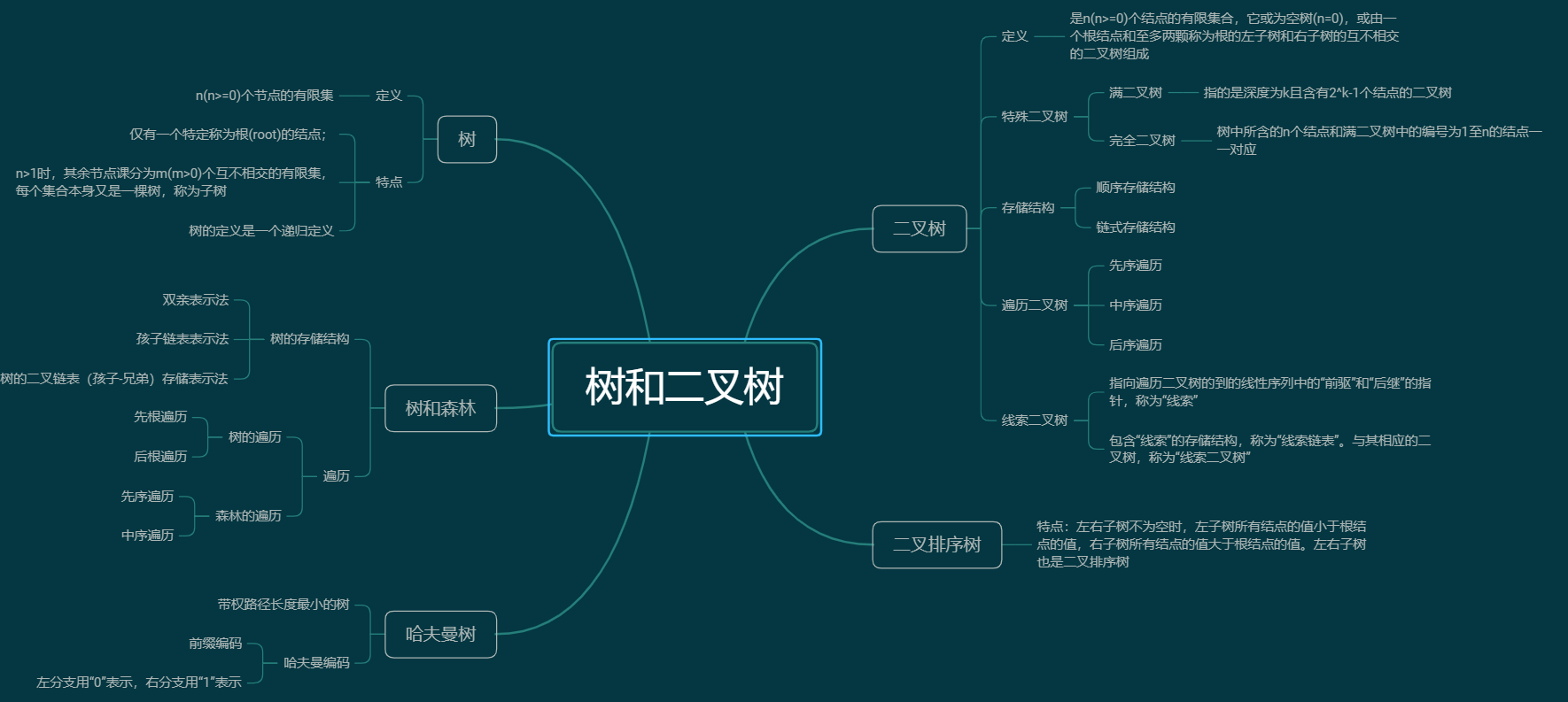
树和二叉树
1.基本术语:
结点:包含-个数据元素及若干指向其子树的分支。
结点的度:结点拥有的子树数。
叶子(或终端)结点:度为零的结点。
分支(或非终端)结点:度大于零的结点。
树的度:树中所有结点的度的最大值。
结点的子树的根称为该结点的孩子(child)。
相应的,该结点称为孩子的双亲(parent)。
同一个双亲的孩子之间互称兄弟。
结点的层次:根结点的层次为1,第l层的结点的子树的根结点的层次为L+1。
双亲在同- -层的结点互为堂兄弟。
树的深度:树中叶子结点所在的最大层次。
森林:是m(m20)棵互不相交的树的集合。
有序树:子树之间存在确定的次序关系(树中结点的各子树从左到右是有次序的,即不能互换)。
无序树:子树之间不存在确定的次序关系。
2.二叉树的性质:
性质1:在二叉树的第i层上至多有2^(i-1)个结点(i>=1)。
性质2:深度为k的二叉树上至多含2^k-1个结点(k>=1)。
性质3:对任何一棵二叉树,若它含有n₀个叶子结点、n₂个度为2的结点,则必存在关系式:n₀=n₂+1。
性质4:具有n个结点的完全二叉树的深度为[㏒₂n+1]
性质5:若对含n个结点的完全二叉树从上到下且从左至右进行1至n的编号,则对完全1 -叉树中任意一个编号为i的结点:
(1)若=1,则该结点是. -叉树的根,无双亲,否则,编号为Li/2.的结点为其双亲结点;
(2)若2i>n,则该结点无左孩子,否则,编号为2i的结点为其左孩子结点;
(3 )若2i+1>n,则该结点无右孩子结点,否则,编号为2i+1的结点为其右孩子结点。
3.二叉链表:
typedef struct BiTNode {
TE lemType data;
struct BiTNode *1child, *rchild;
} BiTNode, *BiTree;
4.遍历二叉树:
void Preorder (BiTree T)
{ //先序遍历二叉树
if (T) {
cout<<T->data;//访问结点
Preorder(T->lchild); //遍历左子树
Preorder(T->rchild); //遍历右子树
}
}
void Preorder (BiTree T)
{ //中序遍历二叉树
if (T) {
Preorder(T->lchild); //遍历左子树
cout<<T->data;//访问结点
Preorder(T->rchild); //遍历右子树
}
}
void Preorder (BiTree T)
{ //后序遍历二叉树
if (T) {
Preorder(T->lchild); //遍历左子树
Preorder(T->rchild); //遍历右子树
cout<<T->data;//访问结点
}
}
5.线索二叉树:
线索链表的类型描述:
typedef struct BiThrNod {
TElemType data ;
struct BiThrNode *1child, *rchild;//左右指针
int LTag, RTag; //左右标志.
} BiThrNode, *BiThrTree;
6.树的遍历和二叉树遍历的对应关系:

7.哈夫曼树
结点的路径长度:从根结点到该结点的路径上分支的数目。
树的路径长度:树中每个结点的路径长度之和。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
在所有含n 个叶子结点、并带相同权值的m叉树中,必存在一-棵其带权路径长度取最小值的树,称为“最优树”。
哈夫曼编码:
关键:要设计长度不等的编码,则必须使任一字符的编码都不是另一个字符的编码的前缀。
符合这种编码要求的编码方式称为前缀编码。
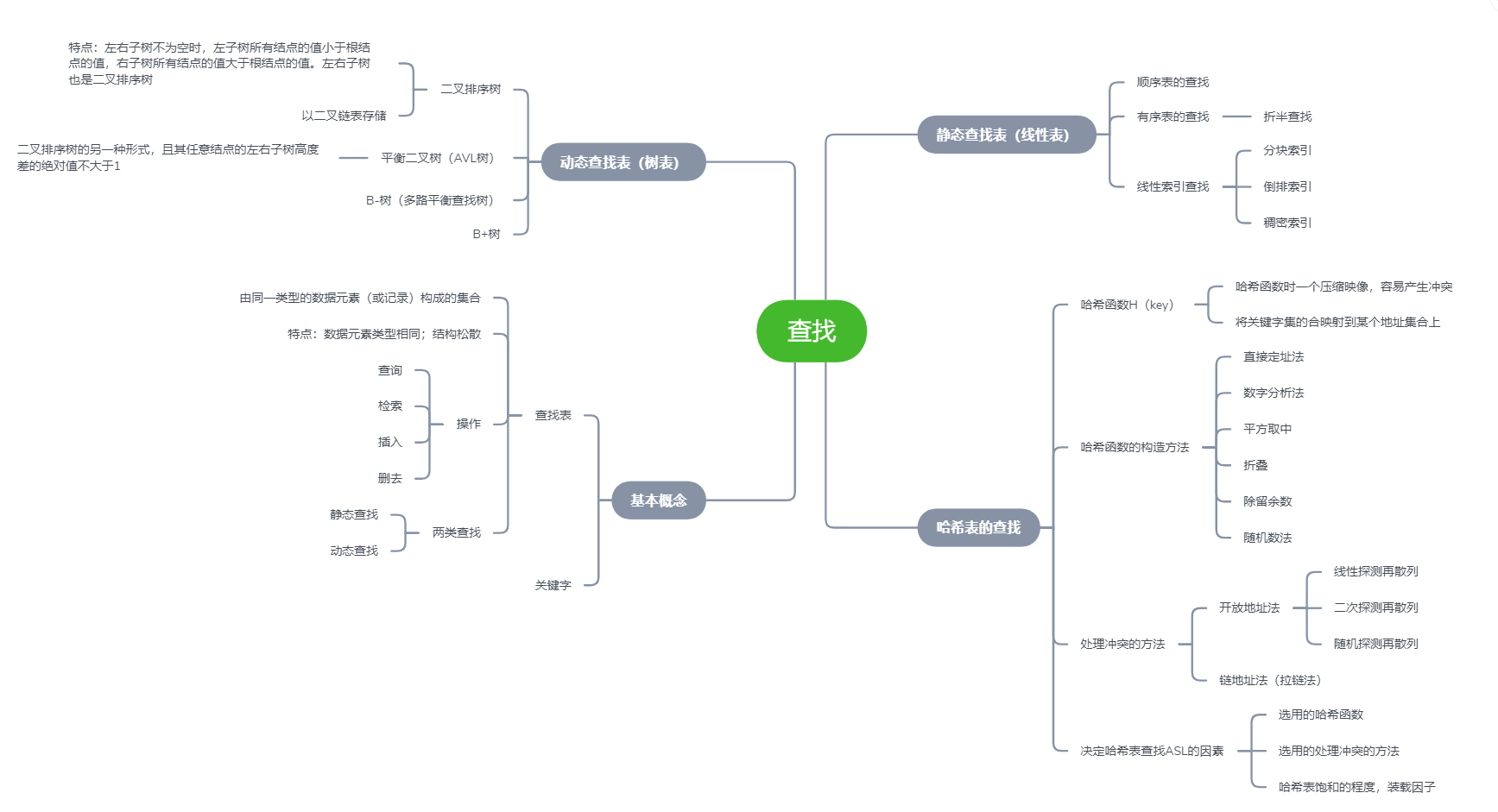
查找
1.折半查找
int Search_ Bin ( SSTable ST, KeyType key ){
low= 1; high = ST.length; // 置区间初值
while (low <= high) {
mid = (low + high) /2;
if (EQ (key , ST.elem[mid].key) )
return mid; //找到待查元素
else if(LT (key , ST.clem[mid].key) )
high = mid- 1; // 继续在前半区间进行查找
else low = mid + 1; //继续在后半区间进行查找
}
return 0; //顺序表中不存在待查元素
} // Search_ Bin
在n>50时,ASL≈㏒₂(n+1)-1
2.二叉排序树:
中序遍历二叉树会得到一个关键字递增的有序序列。
在二叉排序树中查找
void SearchBST(BSTNode T, int key)
{
if (T == NULL || T->Key == key)
return;
else if (key < T->Key)
SearchBST(T->lchild, key);
else
SearchBST(T->rchild, key);
}
在二叉排序树中插入新结点
void InserBST(BSTNode T, int key)
{
if (T == NULL)
{
T = new BSTnode();
T->Key = key;
T->lchild = T->rchild = NULL;
return;
}
else if (T->Key == key)
return;
else if (key < T->Key)
InserBST(T->lchild, key);
else
InserBST(T->rchild, key);
}
创建二叉排序树
void CreateBST(BSTNode &T)
{
int a[100], j, i, n;
j = i = 0;
cin >> n;
for (i = 0; i < n; i++)
cin >> a[i];
while (j<i)
{
InserBST(T, a[j]);
j++;
}
return;
}
3.平衡二叉树(AVL树):
对于一棵有n个结点的AVL树, 其
- 高度保持在O(log₂n)数量级
- ASL也保持在O(log₂n)量级
平衡旋转技术:
LL平衡旋转:
若在A的左子树的左子树.上插入结点,使得A的平衡因子从1增加至2,需要进行一次顺时针旋转。(以B为旋转轴)
RR平衡旋转:
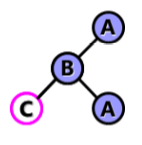
若在A的右子树的右子树.上插入结点,使得A的平衡因子从-1增加至-2,需要进行一次逆时针旋转。(以B为旋转轴)
LR平衡旋转:
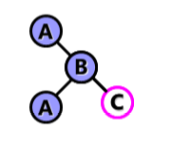
若在A的左子树的右子树上插入结点,使A的平衡因子从1增加至2,需要先进行逆时针旋转,再顺时针旋转。(以插入的结点C为旋转轴)
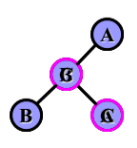
RL平衡旋转:
若在A的右子树的左子树,上插入结点,使A的平衡因子从- 1增加至-2,需要先进行顺时针旋转,再逆时
针旋转。(以插入的结点C为旋转轴)
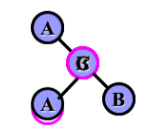
4.B-树和B+树:
B-树和B+树: -一个节点可放多个关键字,降低树的高度。数据可放外存,适合大数据量查找。节点数据从外存中读取,-次读取多个,效率高。应用:目录管理,数据库索引组织。
B-树(多路平衡查找树)的定义:一棵m阶B-树或者时一颗空树,或者是满足下列要求的m叉树:
(1)每个节点至多m个孩子节点(至多有m-1个关键字)。
(2)除根节点外,其他节点至少有[ m/2 ]个孩子节点(即至少有[m/2]-1个关键字) 。
(3)若根节点不是叶子节点,根节点至少两个孩子节点。
B-树主要应用:磁盘管理系统中目录管理、数据库索引。
B+树:文件索引系统中,常使用B-树的变形B+树。B+树是大型索弓文件的标准组织方式。
棵m阶B+树满足下列条件:
(1)每个分支节点至多有m棵子树。
(2)根节点或者没有子树,或者至少有两棵子树
(3)除根节点,其他每个分支节点至少有[ m/2棵子树
(4)有n棵子树的节点有n个关键字。
m阶的B+树和m阶的B -树的差异:
(1)在B+树中,具有n个关键字的节点含有n棵子树,即每个关键字对应一棵子树。而在B-树中,具有n关键字的节点含有n+1棵子树。
(2)在B+树中,每个节点(除根节点外)中的关键字个数n的取值范围是[m/2 ]≤n≤m,根节点n的取值范围是1≤n≤m。而在B-树中,它们的取值范围分别是「m/2]-1≤n≤m-1和1≤n≤m-1。
(3)B+树中的所有叶子节点包含了全部关键字,即其他非叶子节点中的关键字包含在叶子节点中,而在
B-树中,叶子节点包含的关键字与其他节点包含的关键字是不重复的。
(4)B+树中所有非叶子节点仅起到索引|的作用。而在B-树中,每个关键字对应一个记录的存储地址
(5)通常在B+树上有两个头指针,-个指向根节点,另一个指向关键字最小的叶子节点,所有叶子节点链接成一一个不定长的线性链表。
5.哈希表:
哈希函数:建立关键字与记录在表中的存储位置之间的函数关系,以f(key)作为关键字为key的记录在表中的位置,通常称这个函数f(key)为哈希函数。
哈希表的定义:
根据设定的:
哈希函数H(key)
处理冲突的方法
将一-组关键字映像到一个有限的、地址连续的地址集(区间)上,并以关键字在地址集的"像”作 为相应记录在表中的存储位置,如此构造所得的查找表称之为“哈希表”。
关键要素:哈希函数H(key);处理冲突的方法
除留余数法:
设定哈希函数为H(key) = key MOD p
其中,p<=m(表长)并且p应为不大于m的素数或是不含20以下的质因子。
处理冲突的方法:
1.开放地址法:
(1)线性探测再散列:di=c*i最简单的情况c=1
(2)二次探测再散列:di=1²,-1²,2²,-2²,...,±k²(k≤m/2)
(3)随机探测再散列:di是一组伪随机数列或者di=i*H₂(key)(又称双散列函数探测)
2.链地址法(拉链法):
将所有哈希地址相同的记录都链接在同一链表中。
疑难问题
1.问题:平衡二叉树的旋转,碰到复杂的二叉树不知道怎么下手将其旋转成平衡二叉树。
解决:反复观看学习通视频以及课件,大概能将不平衡的二叉排序树转化成平衡二叉排序树。
2.问题:B-树的分裂和合并还不太明白。
未解决
3.删除二叉排序树的结点还云里雾里。
未解决


