最短路径算法
最短路径
我们把边具有权重的图称为带权图,权重可以理解为两点间的距离。一个图中任意两点会有多条路径联通,最短路径就是这些路径中最短的一条。
负环:环中所有边权之重和小于0的环
Floyed算法
算法思想
如何让两个点(假设a到b)的距离变短,只能引入第三个点k,通过k进行中转即a->k->b,当然中转点可以是多个。
算法描述
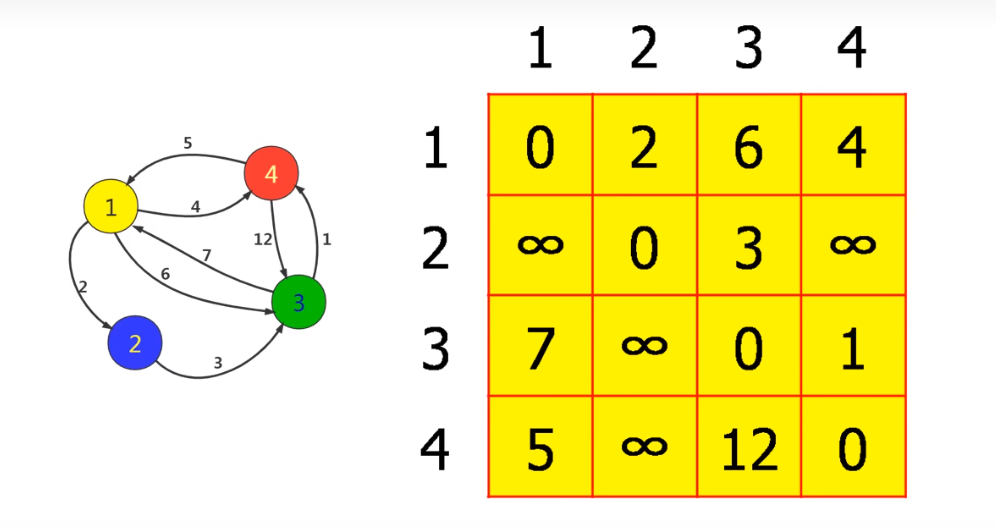
使用邻接矩阵E保存图,每个格子E(i, j)表示点i到点j的最短距离,不相邻的距离为Infinity。遍历每一个点作为中转点k,更新点i与点j的最短路径。
/**
* @param matrix - 邻接矩阵,matrix[i][j]表示点i到j的距离
*/
function Floyed(matrix: number[][]) {
const n = matrix.length
for (let k = 0; k < n; k++) { // 遍历中转点
// 点i到点j的最短距离更新
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
matrix[i][j] = Math.min(matrix[i][j], matrix[i][k] + matrix[k][j])
}
}
}
}
算法总结
- 时间复杂度:O(n^3)
- Floyed算法适用于有负权边的图;但不适用于有负权环的图。
Dijkstra算法
其主要思路如下:
-
将顶点分为两部分:已经知道当前最短路径的顶点集合S和无法到达顶点集合U。
-
定义一个距离数组(distance)记录源点到各顶点的距离,下标表示顶点,元素值为距离。源点(s)到自身的距离为0,源点无法到达的顶点的距离就Infinity。
-
以distance中值最小且在U中(即当前距离最短,非infinity)的顶点v为中转跳点,假设v跳转至顶点w的距离加上源点s到v的距离还小于s到w的距离,那么就可以更新顶点w至源点的距离并把v从U中移除。即:
if(distance[v] + matrix[v][w] < distance[w]) { // matrix邻接矩阵
distance[w] = distance[v] + matrix[v][w]
}
- 重复上一步骤,直到集合U为空。
算法实现
/**
* @param matrix - 邻接矩阵,matrix[i][j]表示点i到j的距离
* @param s - 源点
*/
function Dijkstra(matrix: number[][], s: number) {
const n = matrix.length
const distance: number[] = matrix[s].slice()
const U = new Set<number>()
for (let i = 0; i < n; i++) {
if (distance[i] = Infinity) U.add(i)
}
while (U.size) {
let v: number = -1
U.forEach(drop => {
if (v === -1 || distance[drop] < distance[v]) v = drop
})
if (distance[s] + matrix[s][v] < distance[v]) {
distance[v] = distance[s] + matrix[s][v]
}
U.delete(v)
}
return distance
}
总结
- 时间复杂度O(n^2)
- 需要一个源点
- 不适用于具有负权边的图
Bellman-Ford算法
核心实现:看看引入边side能否使的源点s到点side[1]的距离变短
side数组表示点side[0]到点side[1]的边长为side[2]
算法思路
- 设s为源点,distance[v]为s到v的最短路径,pre[v]为v的前驱,side数组表示点side[0]到点side[1]的边长为side[2]
- 初始化distance[s] = 0, pre[s] = 0。
- 遍历每一条边,如果s到side[0]的距离加上side[2]小于s到side[1]的距离,更新s到side[1]的距离与side[1]的前驱,即:
const start = side[0]
const end = side[1]
const w = side[2]
if (distance[start] + w < distance[end]) {
distance[end] = distance[start] + w
pre[end] = start
}
- 步骤3重复松弛n-1次,如果第i次松弛distance没有更新则已完成。
算法实现
type side = [number, number, number] // side表示点side[0]到点side[1]的边长为side[2]
/**
*
* @param sideList - 边的数组
* @param n - 顶点数,1-n
* @param s - 源点
*/
function Bellman(sideList: side[], n: number, s: number) {
const distance: number[] = new Array(n + 1).fill(Infinity)
const pre: number[] = new Array(n + 1).fill(Infinity)
distance[s] = 0 // 点s到点i的最短距离
pre[s] = 0 // 点s到点i的最短距离前驱
for (let i = 1; i <= n - 1; i++) { // 松弛n-1次
let check = false
sideList.forEach(side => {
const start = side[0]
const end = side[1]
const w = side[2]
if (distance[start] + w < distance[end]) {
distance[end] = distance[start] + w
pre[end] = start
check = true
}
})
if (!check) break
}
}
算法总结
- 时间复杂度O(nm), n定点数,m边数
- 可以处理负权边
SPFA算法--队列优化的Bellman-Ford算法
SPFA是Bellman-Ford算法的一种队列实现,减少了不必要的冗余计算。
主要思想:
初始时将源点加入队列,每次从队列取出一个顶点v,并对v相邻的点k进行修改(与Bellman-Ford算法相同),若相邻点修改成功将其入队,直到队列为空
算法实现
type side = [number, number, number] // side表示点side[0]到点side[1]的边长为side[2]
/**
*
* @param sideList - 边的数组
* @param n - 顶点数,1-n
* @param s - 源点
*/
function SPFA(sideList: side[], n: number, s: number) {
const distance: number[] = new Array(n + 1).fill(Infinity)
const pre: number[] = new Array(n + 1).fill(Infinity)
distance[s] = 0
pre[s] = 0
const queue: number[] = [s]
while (queue.length) {
const v = queue.shift()
sideList.forEach(side => {
const start = side[0]
const end = side[1]
const w = side[2]
if (start === v && distance[start] + w < distance[end]) {
distance[end] = distance[start] + w
pre[end] = start
queue.push(end)
}
})
}
}
算法总结
- 时间复杂度O(kE),E为边数,k为常数,平均值为2,最坏为O(VE)
- 适用于有负权边的图;但不适用于有负权环的图。


