常用优化器及tf源码解析
Optimizer
深度学习中,无法直接找到模型解析解,通常是利用梯度对权重参数做迭代式优化。
经典综述,paper link: https://arxiv.org/pdf/1609.04747.pdf
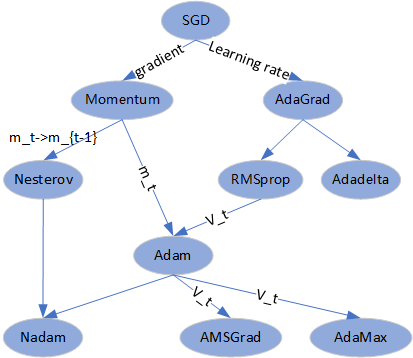
定义后续提到的相关符号,待优化参数 \theta ,目标函数 \(J(\theta)\) ,学习率 lr ,当前epoch/step=t,则当前时刻的参数梯度 \(g_t= \triangledown _{\theta_t} J(\theta_t)\)
后续详细算法前,需要两块知识点为基础,指数加权平均和tensorflow代码结构,放在了最后。
SGD(Stochastic Gradient Descent)
更新公式:\(\theta_t=\theta_{t-1}-lr * g_t\)
关于梯度下降方法,会有三种叫法,BGD/minibatchGD/SGD,区别就是计算 g_t时用多少条样本,全局/小批量/单条。当前DeepLearning任务巨量训练数据默认采用minibatch训练策略,SGD同样默认时minibatchGD。
全局模式每次能够保证梯度都是全局最优方向,缺点就是梯度成本高;单条模式每次更新参数只需要一条样本即可,导致每次迭代不都是朝整体最优方向,波动较大容易在局部最优间跳跃,如果lr 足够小,SGD& BGD会有相同的收敛效果;minibatch结合了前两者在梯度获取上的优势。
但GD系列本身存在固有缺点,1. lr的选择,太小导致收敛速度慢,太大导致局部震荡;2.对于非凸函数容易陷入局部极值点或鞍点,困在梯度为0附近;
class GradientDescentOptimizer():
def _prepare():
_learning_rate_tensor = ops.convert_to_tensor(lr)
def _apply_dense(grad, var):
struct ApplyGradientDescent<CPUDevice, T>
var.device(d) -= grad * lr();
def _apply_sparse_duplicate_indices(grad, var):
delta = ops.IndexedSlices(grad.values * _learning_rate_tensor, grad.indices, grad.dense_shape)
return var.scatter_sub(delta)
Momentum
更新公式:\(\theta_t=\theta_{t-1}-lr * m_t;\ \ m_t=\beta_1*m_{t-1}+(1-\beta_1)*g_t\)
tf代码实现公式:\(\theta_t=\theta_{t-1}-lr * m_t;\ \ m_t=\beta_1*m_{t-1}+g_t\)
既然minibatch相比于batch仍少了数据,自然想到继续计算梯度的数据量,结合指数加权平均思想,使用历史窗口内的数据做平均提高梯度质量。这个历史窗口内的平均,称为梯度的一阶动量 m_t。即保留历史更新方向的同时,利用当前梯度微调最终方向,由于\beta=0.9的默认取值,下降方向主要为积累方向略微偏向当前时刻。
优势在于动量与梯度同向时加速下降,反向时降低速度减少震荡;
缺点在于盲目加速,在接近极值点下降时由于同向加速会造成大幅度跨过极值点。
NAG(Nesterov Accelerated Gradient)
更新公式:\(\theta_t=\theta_{t-1}-lr * m_t;\ \ m_t=\beta_1*m_{t-1}+(1-\beta_1)*\triangledown _{\theta_t} J(\theta_t - \beta_1 *m_{t-1})\)
tf代码实现公式,在Momentum公式中,将m_{t-1}替换为m_t,模拟投影梯度。
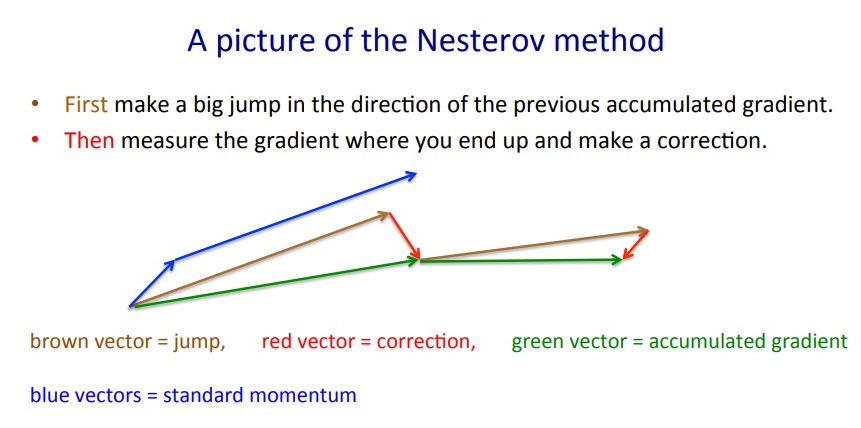
使用先前动量对当前权重更新为投影权重,重新计算前向传播获得投影梯度,用于新动量的计算中。当梯度出现大的跳跃时,通过校正因子对方向进行修正,通过提前预判避免前进的太快,提高灵敏度;
但此方式在随机梯度的情况下,对收敛作用有限。
class MomentumOptimizer():
def __init__():
_lr, _momentum, _use_nesterov
def _create_slots(var_list):
for v in var_list:
momentum -> _zeros_slot(name=v.name+'/momentum')
def _prepare():
_lr_t, _momentum_t <- ops.convert_to_tensor(lr, _momentum)
def _apply_dense(grad, var):
accum = self.get_slot(var, "momentum")
training_ops.apply_momentum()
struct ApplyMomentum<CPUDevice, T> {};
accum.device(d) = accum * momentum() + grad;
if (use_nesterov) {
var.device(d) -= grad * lr() + accum * momentum() * lr();
} else {
var.device(d) -= accum * lr();
}
AdaGrad
更新公式:\(\theta_t=\theta_{t-1}-\frac{lr}{\sqrt {V_t+\epsilon }} * g_t;\ \ V_t=\sum_{i=1}^t g_t^2\)
从参数更新频率角度出发,高频更新的参数经过大量数据的迭代已经得到较高的优化,因此希望降低单条样本对参数的影响,而低频更新参数则反之,由于迭代次数较低希望单条样本对参数的影响更大些,显然只有一个共享标量学习率是不满足需求的。因此引入二阶动量V_t,即所有梯度值的平方和。
缺点是,当 t 越大,分母上的V_t 越大,使得学习率趋于0,导致训练提前结束。
class AdagradOptimizer():
def __init__(lr, initial_accumulator_value=0.1):
epsilon: tf2 1e-8
initial_accumulator_value: tf2 allow zero
def _create_slots(var_list):
for v in var_list:
init = init_ops.constant_initializer(_initial_accumulator_value)
self.add_slot(var, 'accumulator', init)
def _apply_dense(grad, var):
acc = self.get_slot(var, 'accumulator')
training_ops.apply_adagrad()
struct ApplyAdagradV2<CPUDevice, T> {};
accum.device(d) += grad.square();
var.device(d) -= grad * lr() / (accum.sqrt() + epsilon());
RMSprop
更新公式:\(\theta_t=\theta_{t-1}-\frac{lr}{\sqrt {V_t+\epsilon }} * g_t;\ \ V_t=\beta_2*V_{t-1}+(1-\beta_2) g_t^2\)
思想很直接,既然AdaGrad在t 较大时会出问题,那就改变下V_t 的计算公式,不用累计的全部历史梯度而是用近期的部分梯度,结合前边指数加权平均的思想,得到新的窗口V_t 计算方式;默认值 lr=0.001,\beta_2=0.9,\epsilon=10e-6
缺点是,手工设置 lr 对更新影响仍然较大;
class RMSPropOptimizer():
def __init(lr, decay=0.9, momentum=0):
epsilon: tf1->tf2, 1e-10->1e-07
tf1: decay, tf2: rho
centered=False
def _create_slots(var_list):
for var in var_list:
self.add_slot(var, "rms")
self.add_slot(var, "momentum")
if centered:
self.add_slot(var, "mg")
def _prepare():
_lr, _decay, _momentum, _epsilon <- ops.convert_to_tensor
def _apply_dense(grad, var):
rms = self.get_slot(var, "rms")
mom = self.get_slot(var, "momentum")
if not center:
training_ops.apply_rms_prop()
struct ApplyRMSProp<CPUDevice, T> {}
rms.device(d) += (grad.square() - rms) * (1 - rho());
mom.device(d) = mom * momentum() + (grad * lr()) / ((rms + epsilon()).sqrt());
var.device(d) -= mom;
else:
# gradients are normalized by the estimated variance
mg = self.get_slot(var, "mg")
training_ops.apply_centered_rms_prop()
struct ApplyCenteredRMSProp<CPUDevice, T> {}
rms.device(d) += (grad.square() - rms) * (1 - rho());
mg.device(d) += (grad - mg) * (1 - rho());
auto denom = (rms - mg.square()) + epsilon();
mom.device(d) = mom * momentum() + (grad * lr()) / denom.sqrt();
var.device(d) -= mom;
Adadelta
更新公式:\(\theta_t=\theta_{t-1}-lr *\triangledown \theta_{t};\ \ \triangledown \theta_{t}=\frac{\sqrt{D_{t-1}+\epsilon}} {\sqrt{V_t+\epsilon}} g_t;\ \ V_t=\beta_2V_{t-1}+(1-\beta_2)g_t^2;\ \ D_t=\beta_2 D_{t-1}+(1-\beta_2) \triangledown \theta_{t}^2\)
消除了手工设置 lr 的麻烦。
class AdadeltaOptimizer():
def __init__(learning_rate=0.001, rho=0.95):
epsilon: tf1->tf2, 1e-8 -> 1e-7
def _create_slots(self, var_list):
for v in var_list:
self._zeros_slot(v, "accum", self._name)
self._zeros_slot(v, "accum_update", self._name)
def _prepare():
lr, rho, epsilon <- ops.convert_to_tensor
def _apply_dense(grad, var):
accum = self.get_slot(var, "accum")
accum_update = self.get_slot(var, "accum_update")
training_ops.apply_adadelta()
struct ApplyAdadelta<CPUDevice, T> {}
accum.device(d) = accum * rho() + grad.square() * (1 - rho());
const auto update = (accum_update + epsilon()).sqrt() * (accum + epsilon()).rsqrt() * grad;
var.device(d) -= update * lr();
accum_update = accum_update * rho() + update.square() * (1 - rho());
Adam
更新公式:\(\theta_t=\theta_{t-1}- \frac{lr}{\sqrt{\hat V_t + \epsilon} }*\hat m_t\)
\(\hat m_t=m_t/(1-\beta_1^t);\ \ \ m_t=\beta_1 m_{t-1}+(1-\beta_1)g_t=m_{t-1}+(g_t-m_{t-1})(1-\beta_1)\)
\(\hat V_t=V_t/(1-\beta_2^t);\ \ \ V_t=\beta_2 V_{t-1}+(1-\beta_2)g_t^2=V_{t-1}+(g_t^2-m_{t-1})(1-\beta_2)\)
tf代码实现公式:对m_t/V_t做无偏修正时并没有使用幂指 t
在经典GD公式中,参数变化项有两个因素,lr & g_t,Momentum和NAG是在g_t上的工作,AdaGrad/RMSprop/Adadelta是在 lr 上的工作,adam则将两部分改进结合起来,吸收了两侧的优势,虽然仍需要给定 lr 超参,但影响已经很微弱了。默认值,\beta_1=0.9, \beta_2=0.999, \epsilon=10e-8。
class AdamOptimizer():
def __init__(lr=0.001,beta1=0.9,beta2=0.999,epsilon=1e-8):
# epsilon: Default value is 1e-08 in TF1, but 1e-07 in TF2.
self._name = 'Adam'
self.argv = argv
def _create_slots(var_list):
_beta1,_beta2 -> variable(trainable=False) ->self._non_slot_dict
for v in var_list:
m, v -> _zeros_slot(name=v.name+'/Adam') -> self._slots['m'/'v']
def _prepare(self):
_lr_t,_beta1_t,_beta2_t,_epsilon_t <-
ops.convert_to_tensor(lr,beta1,beta2,epsilon)
def _apply_dense(grad, var):
m,v = self.get_slot(var, 'm'/'v')
beta1_power, beta2_power = self._get_beta_accumulators()
struct ApplyAdam<CPUDevice, T> : ApplyAdamNonCuda<CPUDevice, T> {};
const T alpha = lr() * Eigen::numext::sqrt(T(1) - beta2_power()) / (T(1) - beta1_power());
m += (g - m) * (T(1) - beta1());
v += (g.square() - v) * (T(1) - beta2());
var -= (m * alpha) / (v.sqrt() + epsilon());
def _apply_sparse(grad, var):
m,v = self.get_slot(var, 'm'/'v')
beta1_power, beta2_power = self._get_beta_accumulators()
lr = (lr_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power))
m_scaled_g_values = grad * (1 - beta1_t)
m = m * beta1_t
m_t = scatter_add(m, grad.indices, m_scaled_g_values) #sparse add
v_scaled_g_values = (grad * grad) * (1 - beta2_t)
v = v * beta2_t
v_t = scatter_add(v, indices, v_scaled_g_values)
v_sqrt = math_ops.sqrt(v_t)
var_update = state_ops.assign_sub(var, lr * m_t / (v_sqrt + epsilon_t))
NAdam
更新公式:\(\theta_t=\theta_{t-1}- \frac{lr}{\sqrt{\hat V_t + \epsilon} }* M_t\)
\(M_t=\beta_1 \hat m_t + \frac{1-\beta_1}{1-\beta_1^t}g_t;\ \ \hat m_t=m_t/(1-\beta_1^t);\ \ \ m_t=\beta_1 m_{t-1}+(1-\beta_1)g_t\)
\(\hat V_t=V_t/(1-\beta_2^t);\ \ \ V_t=\beta_2 V_{t-1}+(1-\beta_2)g_t^2=V_{t-1}+(g_t^2-m_{t-1})(1-\beta_2)\)
在adam基础上增加了Nesterov ,算是集前人所有方法于一身了。一般而言,在使用带动量的RMSprop或Adam的问题上,使用Nadam可以取得更好的结果。
class Nadam(optimizer_v2.OptimizerV2):
def __init__(lr=0.001,beta_1=0.9,beta_2=0.999,epsilon=1e-7):
self._m_cache
def _create_slots(var_list):
self._m_cache = add_weight('momentum_cache',initializer='ones',trainable=False,)
for var in var_list:
self.add_slot(var, 'm')
self.add_slot(var, 'v')
def _prepare(var_list):
_m_cache_read = tf.identity(self._m_cache)
lr_t, beta_1_t, beta_2_t
local_step, next_step = self.iterations +1, +2
m_t, m_t_1 = beta_1_t
# m_schedule_new = pow(\beta_1, local_step)
m_schedule_new = _m_cache_read * m_t
m_schedule_new = identity(assign(self._m_cache, m_schedule_new))
m_schedule_next = m_schedule_new * m_t_1
def _resource_apply_dense(grad, var):
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
g_prime = grad / (1. - m_schedule_new)
m_t = beta_1_t * m + (1 - beta_1_t) * grad
m_t = state_ops.assign(m, m_t)
m_t_prime = m_t / (1. - m_schedule_next)
m_t_bar = (1 - beta_1_t) * g_prime + m_t_1 * m_t_prime
v_t = beta_2_t * v + (1 - beta_2_t) * square(grad)
v_t = state_ops.assign(v, v_t)
v_t_prime = v_t / (1. - pow(beta_2_t, local_step))
var_t = var - lr * m_t_bar / (sqrt(v_t_prime) + epsilon)
state_ops.assign(var, var_t)
Adamax
更新公式:\(\hat V_t=\beta_2^ \infty V_{t-1}+(1-\beta_2^\infty)|g_t|^\infty=max(\beta_2 V_{t-1},|g_t|)\)
Adam的升级,将V_t计算中的l2 norm推广到了lp norm形式,用于收敛到更稳定的状态;
class Adamax(optimizer_v2.OptimizerV2):
def __init__():
lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-7
def _create_slots(var_list):
for var in var_list:
self.add_slot(var, 'm')
self.add_slot(var, 'v')
def _prepare_local():
local_step = self.iterations + 1
beta_1_t, beta_2_t
beta_1_power = pow(beta_1_t, local_step)
def _resource_apply_dense(grad, var):
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
gen_training_ops.ResourceApplyAdaMax()
struct ApplyAdaMax<CPUDevice, T> : ApplyAdaMaxNonCuda<CPUDevice, T> {};
m.device(d) += (grad - m) * (T(1) - beta1());
// eigen_cwiseMax: an expression of the coefficient-wise max of *this and other
v.device(d) = (beta2() * v).cwiseMax(grad.abs());
var.device(d) -= lr() / (T(1) - beta1_power()) * (m / (v + epsilon()));
AMSGrad
更新公式:\(\theta_t=\theta_{t-1}- \frac{lr}{\sqrt{\hat V_t + \epsilon} }*m_t\)
\(m_t=\beta_1 m_{t-1}+(1-\beta_1)g_t=m_{t-1}+(g_t-m_{t-1})(1-\beta_1)\)
\(\hat V_t=max(\hat V_{t-1},V_t);\ \ \ V_t=\beta_2 V_{t-1}+(1-\beta_2)g_t^2=V_{t-1}+(g_t^2-m_{t-1})(1-\beta_2)\)
论文是ICLR18的bestpaper,表示指数加权的假发使得梯度只有短期记忆,并设计了理论实验证明Adam的收敛失败。但后续的多篇分析表示,虽然论文中表述的确实是Adam存在的问题,但AMSGrad并没有解决。在tf中是一个flag开关控制,集成在了Adam中。
class Adam(optimizer_v2.OptimizerV2):
def __init__(amsgrad=False):
self.amsgrad = amsgrad
def _create_slots(var_list):
if self.amsgrad:
for var in var_list:
self.add_slot(var, 'vhat')
def _resource_apply_dense(grad, var):
vhat = self.get_slot(var, 'vhat')
gen_training_ops.ResourceApplyAdamWithAmsgrad()
class ApplyAdamWithAmsgradOp : public OpKernel {}
functor::ApplyAdamWithAmsgrad<Device, T>()
struct ApplyAdamWithAmsgrad<CPUDevice, T> {}
const T alpha = lr() * sqrt(T(1) - beta2_power()) / (T(1) - beta1_power());
m.device(d) += (grad - m) * (T(1) - beta1());
v.device(d) += (grad.square() - v) * (T(1) - beta2());
vhat.device(d) = vhat.cwiseMax(v);
var.device(d) -= (m * alpha) / (vhat.sqrt() + epsilon());
总结
深度学习可堪称可归结为优化问题,最小化目标函数\(J(\theta)\),首先求解目标梯度\(g_t=\triangledown J(\theta)\),将参数向负梯度方向更新,\(\theta_t=\theta_{t-1}-lr * g_t\),lr为学习率表明前进幅度,梯度表示前进方向。
由公式可看出,参数更新项是两部分决定,因此优化器的发展也分成了为两条思路,最终是Adam将两侧收入麾下。Adam之后的工作,主要集中在m_t和v_t计算方式的改进。
无论怎样发展,所有的改进项都是基于梯度的,一条样本得到的唯一数值只有梯度。直观的,只用当前数值不够好,就需要历史数据的辅助,此时m_t就诞生了;对于较大梯度希望适当缩小,直接操作就是归一化除梯度的模,同样希望历史数据到辅助,就诞生了v_t;具体的区别就是怎样辅助了。
至于哪种优化器效果更好,貌似并没有唯一的结论。大多数的论文中,很少有使用Adam的,而是SGD更多,主要是lr可精细化调整取得最终的那几个小数点的收益。个人觉得,任何时候都可以直接用Adam,跑出baseline后再改动NAdam或 lr+RMSprop 的模式,而非上手就是SGD。Adam不一定是很好的上限,但一定是个不错的下限。
另,对于巨大的稀疏矩阵,尤其是推荐领域EmbeddingDict,tf 中实现Adam是跑不动的,要用LazyAdam,对应pytorch中的SparseAdam。原因在于,单条样本涉及到的embedding在Dict中非常非常少,而m_t& v_t 对于不涉及本次inference的参数也会更新,同时由于Dict size巨大,所以速度就非常慢。sparse模式下的Adam能够反向只更新涉及到的部分embedding行,但对效果可能是有损的。正是由于每次更新所有参数的原因,导致使用Adam的优化算法的GPU利用率会明显高于其他算法,但并没有训练速度上的提升。
准备知识点
指数加权平均
N个数\(x_1,x_2,...,x_N\) , 算术平均 \(\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i\) 当数字存在其他含义时就会存在重要程度的差异(用w表示),对应的加权平均 \(\bar{x}=\frac{1}{N}\sum_{i=1}^N w_ix_i\) 。可以将后者理解为前者的通用式,w=1是退化为前者。
移动窗口策略
随时间变化的数据中,可以使用平均值描述数值的变化趋势。
当数据相对平稳没有剧烈波动时,计算均值可以选取近期部分数据代表整体数据,得到近似平均。
近期数据取多少可以用窗口n表示。n取小值时,均值跟随观测数据较实时,波动较剧烈;n取大值时,均值对波动的平滑效果较好,但需要记录的历史数据较多。因此n的选取,通常使用经验法或试数法,两个极端情况n=1 or n=N。
指数平均加权
指数加权平均是对移动窗口策略的改进,好处在于只需要记录一个数值,去掉了窗口内所有时刻值的保留,节省了内存空间。
记,Vt表示t 时刻的均值,\theta_t 表示t 时刻的观测值,\beta 超参数,则计算公式为,
\(V_t=\beta V_{t-1}+(1-\beta)\theta_t\)
\beta 取值通常默认0.9,详细分析下上边的公式,取 \beta=0.9, t=100;
\(V_{100}=0.9V_{99}+0.1\theta_{100}=0.9(0.9V_{98}+0.1\theta_{99})+0.1\theta_{100}=0.9^2 (0.9V_{97}+0.1\theta_{98})+0.9*0.1\theta_{99}+0.1\theta_{100}\)
\(=0.9^3V_{97}+0.1*0.9^2 \theta_{98}+0.1*0.9\theta_{99}+0.1\theta_{100}\)
指数式递减加权的移动平均,从指数系数观察,0.1*0.9^10=0.03486,普适看来这个值够小可以作为忽略项。从极限公式出发\(limit_{x->0}(1-x)^{1/x}=e\) ,e的倒数约等于0.35,因此可将 1/(1-\beta) 作为忽略项分界点,即指数加权平均可近似为 $ \frac{1}{1-\beta} $ 个数据的窗口平均。
当\beta 越小,越重视当前时刻的观测值,越能够跟随系统瞬间突发变化,时效性强,相对的平稳性稍差。
但此公式存在一个明显的问题点,初始时刻由于积累数据较少导致V的偏差较大,因此存在一种修正偏差方案,\(V_t'=V_t/(1-\beta^t)\) .但在实际使用中,一般不做初期修正,采取忍受熬过;
tensorflow源码
版本TF2.6
class Optimizer
各种具体的优化器,均继承自class Optimizer;暂时只关注单级单卡模式,不涉及分布式;只留核心代码片段和相关参数,去掉变量创建、校验、信息获取,scope命名等;去掉冗余的if 判断,关闭eager模式;
# tensorflow/python/training/optimizer.py
class Optimizer():
def __init__():
self._slots = {}
self._non_slot_dict = {}
def minimize(loss, global_step, var_list):
grads_and_vars = self.compute_gradients(loss, var_list) # type:list(tuple)
return self.apply_gradients(grads_and_vars, global_step)
def apply_gradients(grads_and_vars, global_step):
# g类型规范化;根据v的类型调用不同的变量更新方法;统一收录到converted_grads_and_vars
for g, v in grads_and_vars:
g = ops.convert_to_tensor_or_indexed_slices(g) #type:Tensor/IndexedSlices
p = _get_processor(v)
converted_grads_and_vars.append((g, v, p))
# 创建优化器自带的参数;以及apply梯度前创建好所有必须的tensors
self._create_slots(var_list)
self._prepare()
# 获取参数更新操作op,colocate_with保证op与var在同一设备执行,返回op 集合
for grad, var, processor in converted_grads_and_vars:
with ops.colocate_with(var):
update_ops.append(processor.update_op(self, grad))
apply_updates = control_flow_ops.group(*update_ops)
with ops.control_dependencies([apply_updates]):
apply_updates = state_ops.assign_add(global_step, 1)
return apply_updates
def _get_processor(v):
# resource_variabel类型变量, 调用_resource_apply_dense, _resource_apply_sparse;
# 其余变量, 调用_apply_dense, _apply_sparse
if v.op.type == "VarHandleOp":
return _DenseResourceVariableProcessor(v)
if isinstance(v, variables.Variable):
return _RefVariableProcessor(v)
从基类中可以看出,具体优化器方法实现中,子类至少要实现6个函数,_create_slots, _prepare, _apply_dense, _apply_sparse, _resource_apply_dense, _resource_apply_sparse。
从逻辑上看,_resource_apply_dense & _apply_dense,_resource_apply_sparse & _apply_sparse是相同的。只是获取入参的操作不同,区别并不影响理解逻辑。
resource variabel
关于resource_variable和variable的区别,tf 官方并没有太多的解释,只是在def enable_resource_variables() 中提到了一段,简单总结就是,前者是后者的改进版本,具有内存资源的占用,并且能够保证读写的顺序;
Resource variables are improved versions of TensorFlow variables with a well-defined memory model. Accessing a resource variable reads its value, and all ops which access a specific read value of the variable are guaranteed to see the same value for that tensor. Writes which happen after a read (by having a control or data dependency on the read) are guaranteed not to affect the value of the read tensor, and similarly writes which happen before a read are guaranteed to affect the value. No guarantees are made about unordered read/write pairs.
看完这段并没有什么理解,在variables.py里翻看,看到官方给的demo,并且结合运行结果,有点懂了。
import tensorflow as tf
# import tensorflow.compat.v1 as tf
# tf.disable_eager_execution()
# tf.disable_resource_variables()
# tf.disable_control_flow_v2()
tf.reset_default_graph()
print(tf.__version__)
def my_false_fn():
return 0
v = tf.Variable(5)
res = tf.cond(v>4, lambda: v.assign(3), my_false_fn)
# from tensorflow.python.ops import resource_variable_ops
# resource_variable_ops.is_resource_variable(v)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print(sess.run([res,v]))
在 tf1.9 版本中,output: [3, 3];在tf2.x中,output: [3, 5]
首先明确一点,sess.run的顺序并不影响graph流的先后,因此[res, v]还是[v, res],结果是完全一样的。
举个例子,1+1=10,这在二进制下是正确,但看到之后要多反应一下。类比到demo,个人认为,3/5 都有各自的逻辑,5 更合理些但3也不是完全错,只要有规则可循提前定义好就行,但偏偏 tf 把这块模糊了,在 tf1.get_variable中有一个参数就是使用use_resource。
tensorflow在2.x后将ResourceVariable作为默认项,Variable是一个resource,继承自ResourceBase并由ResourceMgr管理。
对应到optimizer里,就是为啥会有apply_dense和resource_apply_dense两个看起来没啥区别的函数实现。
Adam文件查找
在tensorflow/python/training下集成了官方提供的一众优化器实现,但具体看进去就发现,有点头疼。
以adam.py为例,_apply_dense()调用了training_ops.apply_adam,但training_ops.py算上注释也就26行内容,又是一个import嵌套。from tensorflow.python.ops import gen_training_ops ,在源码中找到ops文件夹,发现并没有gen_training_ops.py文件,一脸懵逼!
在编译安装的机器上搜索,居然存在这个文件。前两行表明这是个生成文件,并且来源于cpp。
This file is MACHINE GENERATED! Do not edit.
Original C++ source file: training_ops.cc
tensorflow使用bazel编译器,编译依赖关系在BUILD文件中,虽然知道了来源,但还是尝试从源码中查找下流程。
首先搜索training_ops_gen,在tensorflow/python/BUILD中发现编译输出,
tf_gen_op_wrapper_private_py(
name = "training_ops_gen",
out = "training/gen_training_ops.py",
)
跟进tf_gen_op_wrapper_private_py,发现调用tf_gen_op_wrapper_py接口
tf_gen_op_wrapper_py(
name = "training_ops,
out = "training/gen_training_ops.py",
require_shape_functions = True,
generated_target_name = name,
api_def_srcs = [
"//tensorflow/core/api_def:base_api_def",
"//tensorflow/core/api_def:python_api_def",
],
)
deps = ["//tensorflow/core:" + name + "_op_lib"]
继续进入def定义
if not deps:
deps = [str(Label("//tensorflow/core:" + name + "_op_lib"))]
转到core/BUILD中查找training_ops,在tf_gen_op_libs下一坨,节选
tf_gen_op_libs(
is_external = False,
op_lib_names = ["training_ops",],
deps = [
":lib",
":protos_all_cc",
],
)
进入def tf_gen_op_libs执行
n=training_ops
native.cc_library(
name = n + "_op_lib",
copts = tf_copts(is_external = is_external),
srcs = ["ops/" + n + ".cc"],
deps = deps + [clean_dep("//tensorflow/core:framework")],
visibility = ["//visibility:public"],
alwayslink = 1,
linkstatic = 1,
)
至此找到,src: ops/training_ops.cc。
由tf 模式可知,ops对应定义,具体实现在kernel中去找。
kernel中有eigen库版本的cpu版本,以及cuda写的GPU版本,能够起到任务加速。
Reference
指数移动平均:https://zhuanlan.zhihu.com/p/32335746 http://shichaoxin.com/2020/02/25/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E5%9F%BA%E7%A1%80-%E7%AC%AC%E5%8D%81%E5%85%AD%E8%AF%BE-%E6%8C%87%E6%95%B0%E5%8A%A0%E6%9D%83%E5%B9%B3%E5%9D%87/
Opt: https://www.cnblogs.com/guoyaohua/p/8542554.html https://zhuanlan.zhihu.com/p/58236906 https://mp.weixin.qq.com/s/EOVvSPeEMbcj2tJnOk1zTA https://cloud.tencent.com/developer/article/1468547?from=article.detail.1183236
Tf: https://zhuanlan.zhihu.com/p/87348147 https://www.cnblogs.com/littleorange/p/13168159.html https://blog.51cto.com/u_15179348/2734068

