CTR预估模型
CTR预估模型
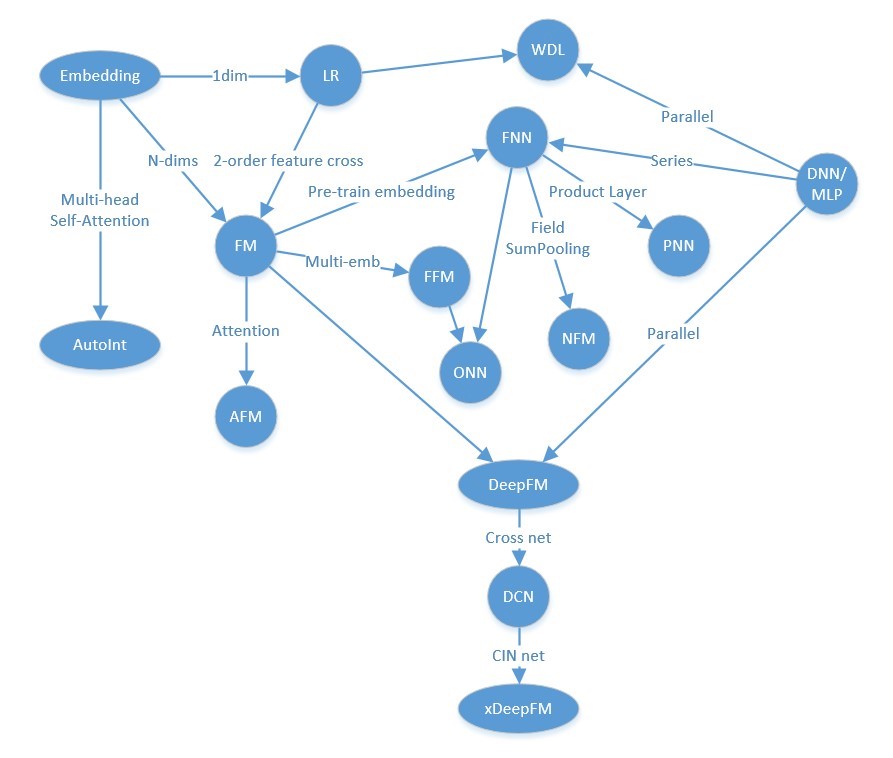
本文主要是为了将ctr模型的历程整理分类,并记录各模型的重点部分。所示代码几乎都不能直接运行,而是力求将模型核心部分体现出来。这和我自己的定位有关,自己在学习看代码的时候我只是想知道模型干了什么怎么实现的,至于数据处理部分我并不关心,不同场景有不同的处理脚本。因此只想记录下各个模型的核心实现。
下边这种图连接线会五花八门的,不同人会有不同的理解角度,随便看看就好。
LR
优点:模型简单;时间复杂度低;可大规模并行化;具备一定可解释性;
缺点:依赖大量特征工程;特征交叉困难;未出现的数据泛化性差;
公式:
def lr1(x_id, feature_size):
"""
x_id: input, feature id;
feature_size: feature variable space
"""
embeddings = tf.Variable(tf.random_uniform([feature_size,], -0.1, 0.1))
b = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
preds = b
preds += tf.reduce_sum(tf.nn.embedding_lookup(embeddings, x_id))
preds = tf.clip_by_value(tf.sigmoid(preds), 1e-5, 1.0 - (1e-5), name='preds')
loss = tf.reduce_mean(tf.losses.log_loss(predictions=preds, labels=_Y))
def lr2(x_onehot, feature_size):
"""
x_onehot: input, onehot(feature_id), size=feature_size;
feature_size: feature variable space
"""
embeddings = tf.Variable(tf.random_uniform([feature_size,], -0.1, 0.1))
b = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
preds = b
# tf.sparse_tensor_dense_matmul if x_onehot is sparse tensor
preds += tf.reduce_sum(tf.multiply(embeddings, x_onehot))
return preds
say something:
公式是按照onehot的输入形式给出的,将特征进行onehot展开,输入长度与特征空间长度相同,输入与embedding词表相乘得到对应行的映射权重,即代码 lr2 中实现方式;
但在实际工程中,考虑到输入维度较高、内存以及sparse2dense实现效率的问题,通常是采用代码 lr1 中实现方式,输入为原始id特征,采用embedding_lookup查询到对应行的映射权重。
对于dense feature的处理,先进行embedding_lookup得到embedding,再用dense feature原始数据进行scale, 即\(v_ix_i\)
embedding dict
标准写法是为每一个field创建一个对应的embedding dict,[emb_dict(space) for space in fieldspacelist],好处是能隔离开不同field,缺点就是需要维护的向量词表较多;
另一种实现形式就是开辟一个超大的embedding映射空间,将feature_id+namespace组合hash到映射空间内,好处是减少词表维护量,缺点就是耦合了所有field会存在hash冲突导致映射向量的不准;
从经验来看,如果hash方法合适的话,产生hash冲突的概率很小。因此,本文默认采用后者,即模型中只存在一个embedding dict,所有的输入都是经过hash编码后的。
FM: Factorization Machines, 2010
出发点:LR需要手动构造交叉特征;\(x_i\)=(gender='man' & city='Beijing'),只有两个特征均为 1 时才能更新训练对应的权重;学习不到训练集中未出现的交叉特征,泛化性不好。
优点:可有效处理稀疏场景下的特征学习;具有线行时间复杂度;对训练集中未出现的交叉特征也可进行泛化;
缺点:仅枚举了所有二阶交叉特征,没有考虑高阶;
公式:
D: embedding dim
def fm(x_id, feature_size, dim):
"""
x_id: input, feature id, tensor_shape=[Batch, field];
feature_size: feature variable space
dim: embedding size
"""
embemdding_matrix = tf.Variable(tf.random_uniform([feature_size, dim], -0.1, 0.1), dtype=tf.float32)
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
square_of_sum = tf.square(tf.reduce_sum(emb_vec, 1))
sum_of_square = tf.reduce_sum(tf.square(emb_vec), 1)
cross_term = square_of_sum - sum_of_square
preds = 0.5 * tf.reduce_sum(cross_term, 2)
return preds
say something:
强制要求所有field的embedding向量的维数,增加了网络复杂度;对连续值特征不友好。
FFM: Field-aware Factorization Machine, 2016
出发点:每个特征xi的隐向量应该有多个,当该特征与不同类型(域field)的特征做交叉时,应该使用对应的隐向量,这样可以做到更精细地刻画交叉特征的权重。所以每个特征应该有和field数量相同的隐向量个数。
优点:引入不同field交叉向量,增加了模型表达能力;
缺点:浅层模型,没有学到高阶交叉特征;
公式:
fj是第j个特征所属的field。
def ffm(x_id, feature_space_list, dim):
"""
x_id: input, feature_id, tensor_shape=[Batch, field]
feature_space_list: a list of feature variable space
dim: embedding size
"""
def gen_emb_dict(space_size, dim_size):
return tf.Variable(tf.random_uniform([space_size, dim_size], -0.1, 0.1), dtype=tf.float32)
embemdding_matrix = [[gen_emb_dict(i, dim) for j in feature_space_list] for i in feature_space_list]
def feature_embedding(fc_i, fc_j, embedding_dict, input_feature):
fc_i_embedding = tf.nn.embedding_lookup(embedding_dict[fc_i][fc_j], input_feature) #shape=(B,D)
return fc_i_embedding
embed_list = []
for fc_i, fc_j in itertools.combinations(range(len(feature_space_list))):
i_input = x_id[:,fc_i]
j_input = x_id[:,fc_j]
fc_i_embedding = feature_embedding(fc_i, fc_j, embemdding_matrix, i_input)
fc_j_embedding = feature_embedding(fc_j, fc_i, embemdding_matrix, j_input)
element_wise_prod = tf.reduce_sum(fc_i_embedding * fc_j_embedding, -1)
embed_list.append(element_wise_prod)
ffm_cross = tf.concat(embed_list, axis=1)
ffm_out = tf.reduce_sum(ffm_cross, -1)
say something:
收益更多的来自扩展了模型参数空间,简单粗暴但有收益,在工业场景落地则对计算资源要求极高。
AFM: Attention Factorization Machines, 2017
出发点:FM枚举所有二阶交叉特征,但部分交叉特征与预估目标关联性不大(如广告位尺寸与性别的交叉)。
优点:在FM基础上引入Attention机制,赋予不同交叉特征不同的重要程度;一定程度上增加了模型的可解释性;
缺点:仍是一种浅层模型,没有学到高阶交叉特征
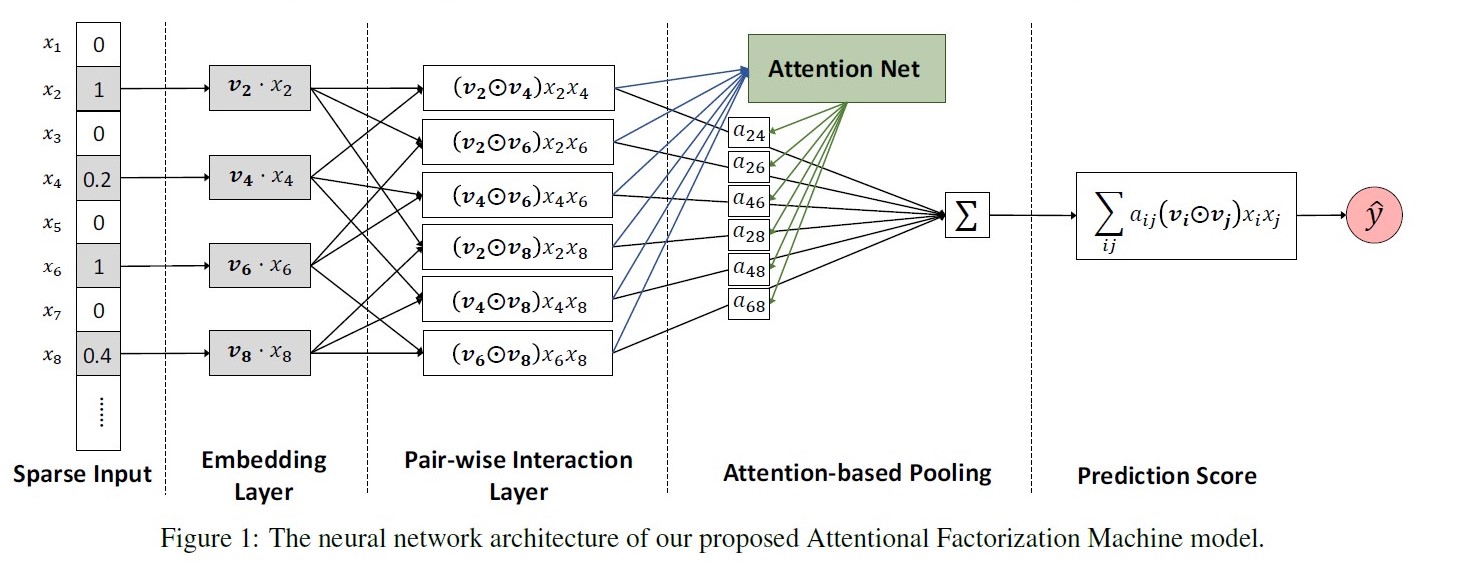
公式:
\(\bigodot\) : element-wise
def AFM(x_id, feature_size, dim, attention_factor)
"""
x_id: input, feature id, shape=[Batch, field]
feature_size: feature variable space
dim: embedding size
attention_factor: dimensionality of the attention network output space.
"""
field_size = x_id.get_shape().as_list()[1]
embemdding_matrix = tf.Variable(tf.random_uniform([feature_size, dim], -0.1, 0.1), dtype=tf.float32)
attention_W = tf.Variable(tf.random_uniform([dim, attention_factor], -0.1, 0.1), dtype=tf.float32)
attention_b = tf.Variable(tf.random_uniform([attention_factor,], -0.1, 0.1), dtype=tf.float32)
projection_h = tf.Variable(tf.random_uniform([attention_factor, 1], -0.1, 0.1), dtype=tf.float32)
projection_p = tf.Variable(tf.random_uniform([embedding_size, 1], -0.1, 0.1), dtype=tf.float32)
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
# element_wise, inner_product
embeds_vec_list = tf.split(emb_vec, field_size, 1) # [(B,1,D)]*F
row = []; col = []
import itertools
for r, c in itertools.combinations(embeds_vec_list, 2):
row.append(r)
col.append(c)
p = tf.concat(row, axis=1) #pair = (F*F-F)/2, shape(B, pair, D)
q = tf.concat(col, axis=1)
inner_product = p * q
# ###another: element_wise, inner_product
# inner_product_list = []
# for i in range(field_size):
# for j in range(i+1, field_size):
# tmp = tf.multiply(emb_vec[:,i,:], emb_vec[:,j,:])
# inner_product_list.append(tmp) # shape=[B,D]
# inner_product = tf.stack(inner_product_list) # shape=[pair,B,D]
# inner_product = tf.transpose(inner_product, perm=[1,0,2]) # shape=[B,pair,D]
attention_temp = tf.nn.relu(tf.tensordot(inner_product, attention_W, axes=(-1, 0)) + attention_b)
normalized_att_score = tf.nn.softmax(tf.tensordot(attention_temp, projection_h, axes=(-1, 0)), dim=1) # shape=[B,pair,1]
attention_output = tf.reduce_sum(normalized_att_score * inner_product, axis=1) # shape=[B,D]
afm_out = tf.tensordot([attention_output, projection_p]) # shape=[B,1]
return afm_out
say something:
AFM是FM的泛化形式,当\(p=[1,1,...,1]^T \quad and \quad \alpha_{ij}=1\)时,AFM退化成FM模型。
FNN: Factorisation Machine supported Neural Network, 2016
出发点:FM没有考虑高阶交叉特征,DNN具备高阶特征交叉能力。
优点:离线训练FM得到embedding再输入NN,相当于引入先验经验;加速模型的训练和收敛;NN模型节省了学习特征向量的步骤,训练开销低;
缺点:两阶段模型,非endtoend,不利于online learning;预训练embedding受FM模型的限制;只考虑了特征的高阶交叉,没有保留低阶特征信息;

模型:
将FM预训练好的embedding向量直接输入下游DNN
def FNN(x_id, embemdding_matrix, layer_size):
"""
x_id: input, feature id, shape=[Batch, field]
embedding_matrix: pretrain FM model embedding vector
layer_size: a list of DNN layer size, [200,80,1]
"""
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
enc = emb_vec
for i in layer_size:
enc = tf.layers.dense(enc, i, activation=tf.nn.leaky_relu)
return enc
PNN: Product-based Neural Network, 2016
出发点:DNN中特征向量通过简单concat or add都不足以学习到特征之间的依赖关系,因此需要引入更复杂和充分的特征交叉关系的学习。
优点:通过z部分保留了低阶embedding特征信息;通过product layer引入更复杂的特征交叉方式;
缺点:计算时间复杂度相对较高;product函数的实现直接决定了落地可行性;
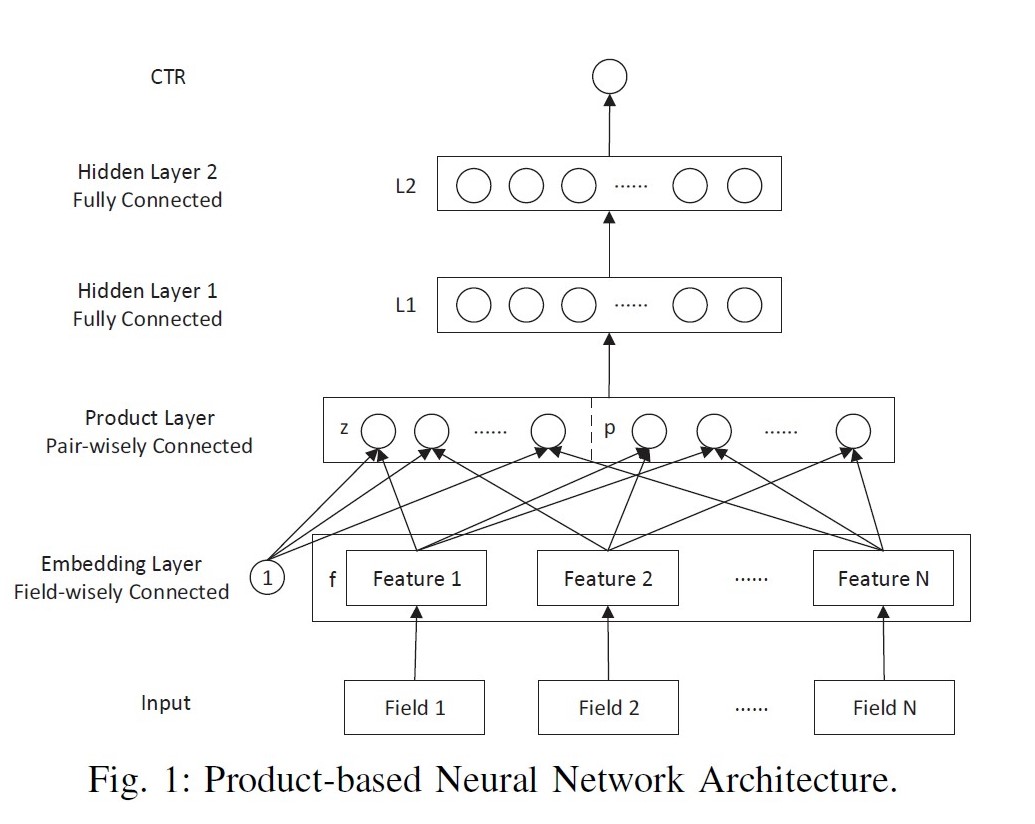
模型:
将每个field的embedding向量输入product layer,在product layer中包含了两部分,一部分是左边的z 直接保留了embedding向量,另一部分右边的p (pair-wise特征交叉)是对应特征之间的product操作。
Product layer:inner product, outer product, kernel product;
对于内积形式的PNN, 两向量相乘的结果为标量,可以直接把各个标量concat拼接成一个大向量,作为MLP的输入。
对于外积形式的PNN, 两向量相乘相当于列向量与行向量进行矩阵相乘,得到结果为一个矩阵。论文简化方案是将各个矩阵进行加和,得到新矩阵拉长成向量后输入MLP。
公式:D is embedding dim; \(D_{L1}\) is L1 layer size;
IPNN:
P矩阵flatten后就是全连接操作,\(W_p=shape[(F\*F),D_{L1}]\)
OPNN:
def PNN(x_id, feature_size, dim)
"""
x_id: input, feature id, shape=[Batch, field]
feature_size: feature variable space
dim: embedding size
"""
field_size = x_id.get_shape().as_list()[1]
embemdding_matrix = tf.Variable(tf.random_uniform([feature_size, dim], -0.1, 0.1), dtype=tf.float32)
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
# inner_product
embeds_vec_list = tf.split(emb_vec, field_size, 1) # [(B,1,D)]*F
row = []; col = []
import itertools
for r, c in itertools.combinations(embeds_vec_list, 2):
row.append(r)
col.append(c)
p = tf.concat(row, axis=1) #pair = (F*F-F)/2, shape(B, pair, D)
q = tf.concat(col, axis=1)
inner_product = p * q #shape(B, pair, D)
inner_product = tf.reduce_sum(inner_product, axis=2)
# outer product
embedding_sum = tf.reduce_sum(emb_vec,axis=1)
p = tf.matmul(tf.expand_dims(embedding_sum,2),tf.expand_dims(embedding_sum,1)) # shape=[B,D,D]
outer_product = tf.layers.flatten(p)
# kernel product
row = []; col = []
for i in range(field_size - 1):
for j in range(i + 1, field_size):
row.append(i)
col.append(j)
# shape=[B,pair,D]
p = tf.transpose(
# shape=[pair,B,D]
tf.gather(
# shape=[F,B,D]
tf.transpose(emb_vec, [1, 0, 2]),
row),
[1, 0, 2])
q = tf.transpose(
tf.gather(
tf.transpose(emb_vec, [1, 0, 2]),
col),
[1, 0, 2])
num_pairs = len(row)
p = tf.reshape(p, [-1, num_pairs, dim])
q = tf.reshape(q, [-1, num_pairs, dim])
kernel = tf.Variable(tf.random_uniform([dim, num_pairs, dim], -0.1, 0.1), dtype=tf.float32)
p = tf.expand_dims(p, 1)
# shape=[B,pair,D]
kp = tf.multiply(
# shape=[B,pair,D]
tf.transpose(
# shape=[B,D,pair]
tf.reduce_sum(
# shape=[B,D,pair,D]
tf.multiply(p, self.kernel),
-1),
[0, 2, 1]),
q)
# shape=[B,pair]
kernel_product = tf.reduce_sum(kp, -1)
公式优化:IPNN通过矩阵分解跳过显示productlayer,通过代数转换直接从embedding到了L1隐层;OPNN直接在productlayer进行优化;
IPNN:
L1层空间复杂度\(O(D_{L1}FD+D_{L1}F^2)->O(D_{L1}FD)\);时间复杂度\(O(D_{L1}FD+D_{L1}F^2)->O(D_{L1}FD+D_{L1}D^2)\)
OPNN:
L1层时间空间复杂度\(O(D_{L1}D^2F^2)->O(D_{L1}DF+D_{L1}D^2)\),信息同样损失严重。
def PNN():
quadratic_output = []
if use_inner:
weights['inner'] = tf.Variable(tf.random_normal([L1_size,field_size],0.0,0.01))
for i in range(L1_size):
theta = tf.multiply(emb_vec,tf.reshape(weights['inner'][i],(1,-1,1))) # shape=(B,F,D)
quadratic_output.append(tf.reshape(tf.norm(tf.reduce_sum(theta,axis=1),axis=1),shape=(-1,1))) # shape=(B,1)
elif use_outer:
weights['outer'] = tf.Variable(tf.random_normal([L1_size, field_size,field_size], 0.0, 0.01))
embedding_sum = tf.reduce_sum(emb_vec,axis=1)
p = tf.matmul(tf.expand_dims(embedding_sum,2),tf.expand_dims(embedding_sum,1)) # shape=(B,D,D)
for i in range(L1_size):
theta = tf.multiply(p,tf.expand_dims(self.weights['outer'][i],0)) # shape=(B,D,D)
quadratic_output.append(tf.reshape(tf.reduce_sum(theta,axis=[1,2]),shape=(-1,1))) # shape=(B,1)
lp = tf.concat(quadratic_output,axis=1)
say something:
这实际是一篇会转刊的文章,网上能搜到两个版本,一个是2016年的ICDM,一个是2018年的TOIS,在转刊时不能完全相同,因此文章把outer product部分替换成了kernel product;kernel的设计更复杂了,但还是outer的泛化,把kernel看成tf.ones()就会退化到outer,
NFM: Neural Factorization Machines, 2017
出发点:FM枚举所有二阶交叉特征,没有高阶交叉特征
优点:相比于concat操作,NFM在low level进行interaction可以提高模型的表达能力;具备一定高阶特征交叉能力;Bi-Interaction Pooling的交叉具备线性复杂度;
缺点:直接进行sum pooling操作会损失信息,可参考AFM的操作;
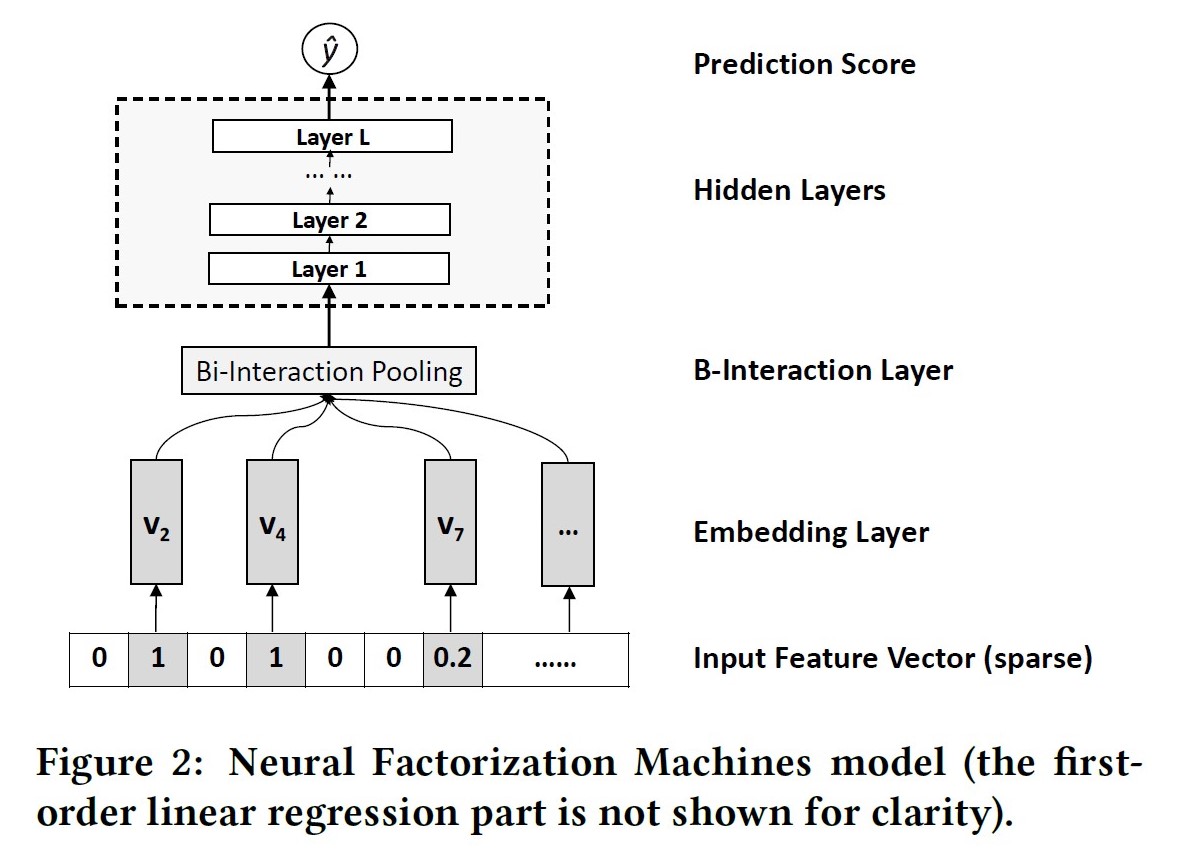
公式:
Bi-Interaction操作,名字挺高大上,其实就是一个计算FM的过程,将所有二阶交叉结果向量在field维度进行sum pooling后再送入NN进行训练。
def bi_interaction(x_id, feature_size, dim):
"""
x_id: input, feature id, tensor_shape=[Batch, field];
feature_size: feature variable space
dim: embedding size
"""
embemdding_matrix = tf.Variable(tf.random_uniform([feature_size, dim], -0.1, 0.1), dtype=tf.float32)
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
square_of_sum = tf.square(tf.reduce_sum(emb_vec, 1))
sum_of_square = tf.reduce_sum(tf.square(emb_vec), 1)
cross_term = 0.5 * (square_of_sum - sum_of_square)
return cross_term
say something:
当NN的全连接都是恒等变换且最后一层参数全为1, NFM就退化为FM。NFM是FM的推广,延迟了FM的实现过程,在其中加入更多非线形运算。
ONN: Operation-aware Neural Network, 2019
出发点:不同的特征交叉操作,应该使用不同的embedding,相同的embedding在不同操作间会相互影响而最终限制了模型的表达。
优点:引入Operation-aware,增加了模型表达能力;同时包含了特征一阶信息和高阶交叉信息;
缺点:模型复杂度高;每个feature对应多个embedding结果;
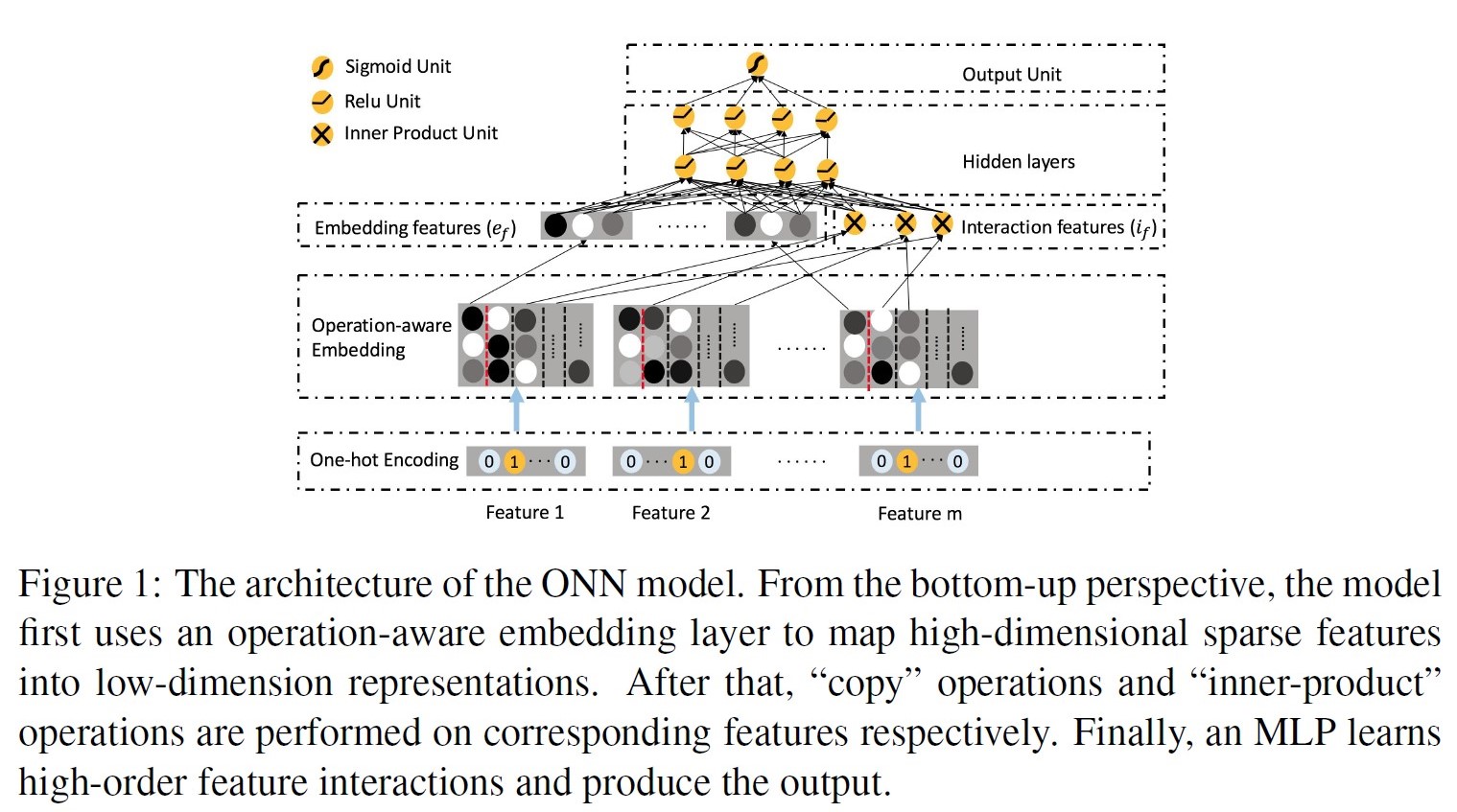
模型:
一个feature对应多个embedding,第一列的embedding是feature本身的信息,从第二列开始往后是当前特征与第n个特征交叉所使用的embedding。
def ONN(x_id, feature_space_list, dim):
"""
x_id: input, feature_id, tensor_shape=[Batch, field]
feature_space_list: a list of feature variable space
dim: embedding size
"""
def gen_emb_dict(space_size, dim_size):
return tf.Variable(tf.random_uniform([space_size, dim_size], -0.1, 0.1), dtype=tf.float32)
embemdding_matrix = [[gen_emb_dict(i, dim) for j in feature_space_list] for i in feature_space_list]
def feature_embedding(fc_i, fc_j, embedding_dict, input_feature):
fc_i_embedding = tf.nn.embedding_lookup(embedding_dict[fc_i][fc_j], input_feature) #shape=(B,D)
return fc_i_embedding
embed_list = []
for fc_i, fc_j in itertools.combinations(range(len(feature_space_list))):
i_input = x_id[:,fc_i]
j_input = x_id[:,fc_j]
fc_i_embedding = feature_embedding(fc_i, fc_j, embemdding_matrix, i_input)
fc_j_embedding = feature_embedding(fc_j, fc_i, embemdding_matrix, j_input)
element_wise_prod = tf.reduce_sum(fc_i_embedding * fc_j_embedding, -1)
embed_list.append(element_wise_prod)
onn_cross = tf.concat(embed_list, axis=1)
onn_out = DNN(onn_cross)
say something:
模型结构并没有太惊艳,积木拼接FFM+NN=ONN。
FFM/AFM/ONN通过引入额外的信息来区分不同field间的交叉应该具备不同的信息表达和重要性。
WDL: Wide and Deep Learning, 2016
出发点:首次使用双路并行的结构,结合Wide线行模型的记忆性(memorization)和Deep深度模型的泛化性(generalization)来对用户行为信息进行学习建模。
优点:Wide&Deep互补,Deep弥补Memorization层泛化性不足的问题;wide&deep joint training可减少wide部分的model size(即只需要少数的交叉特征);可以同时学习低阶特征交叉wide和高阶特征交叉deep;
缺点:仍需要手动设计交叉特征;

公式:
def wdl(x_id, feature_size):
embeddings = tf.Variable(tf.random_uniform([feature_size,], -0.1, 0.1))
b = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
inp = tf.nn.embedding_lookup(embeddings, x_id)
lr = tf.reduce_sum(inp)
nn = DNN(inp)
preds = b+lr+nn
DeepFM: Deep Factorization Machines, 2017
出发点:FM基础上引入NN隐式高阶交叉信息;
优点:模型同时学习低阶和高阶特征能力;共享embedding,共享参数信息表达;
缺点:DNN部分对于高阶特征的学习仍然是隐式的;
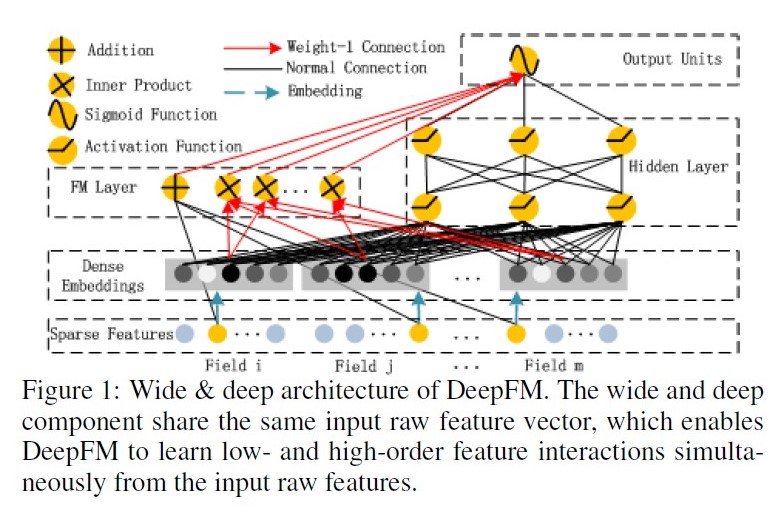
公式:
DCN: Deep and Cross Network, 2017
出发点:DNN的高阶交叉学习能力是隐式的,wide侧的交叉组合特征主要是人工特征工程或暴力搜索(exhaustive searching),因此提出cross net可以显示的学习有限阶(bounded degrees)的特征交叉;
优点:具备显示高阶特征交叉能力;结合ResNet思想,将原始信息在crossnet中跳跃传递;crossNet结构简单,节省内存计算高效;
缺点:CrossNet在进行交叉时采用bit-wise方式,直接concat淹没了field的概念;每层的输出都是输入向量\(x_0\)的标量倍(不是线行倍),这种形式在一定程度上限制了模型的表达能力;
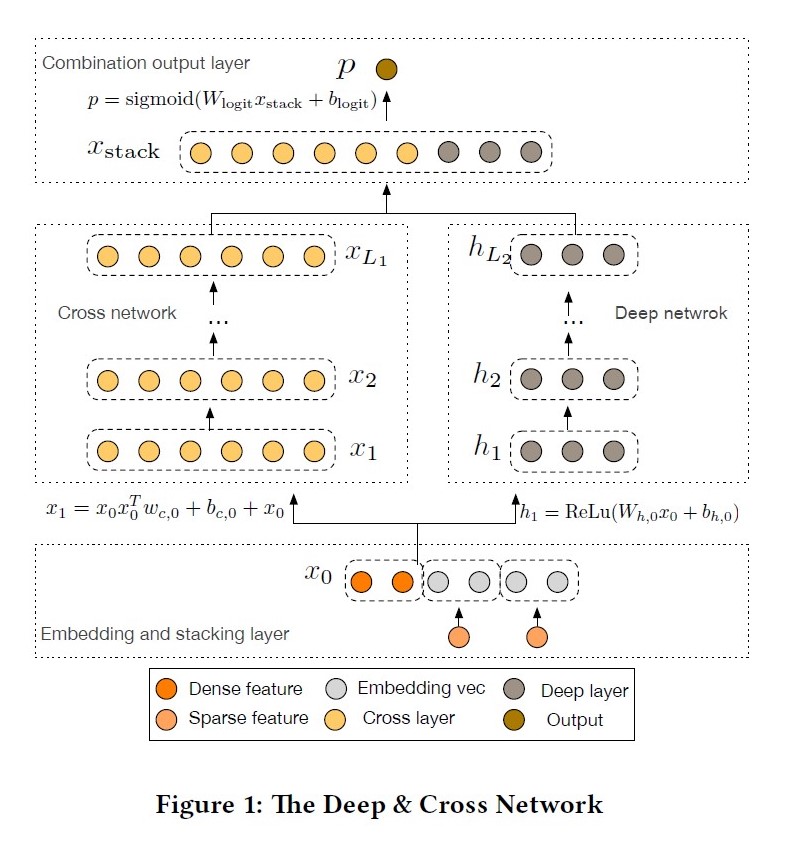
公式:
证明:输出都是输入向量\(x_0\)的标量倍(忽略偏置项)
def cross_layer(x0, x, name):
"""
x0,x: input tensor, shape=(B,N)
"""
with tf.variable_scope(name):
input_dim = x0.get_shape().as_list()[1]
w = tf.get_variable("weight", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
b = tf.get_variable("bias", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
xb = tf.tensordot(tf.reshape(x, [-1, 1, input_dim]), w, 1)
return x0 * xb + b + x
def build_cross_layers(x_id, feature_size, dim, num_cross_layers, hidden_size_lst):
embemdding_matrix = tf.Variable(tf.random_uniform([feature_size, dim], -0.1, 0.1), dtype=tf.float32)
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
B = emb_vec.get_shape().as_list()[0]
x0 = tf.reshape(emb_vec, [B,-1]) # shape=(B,N), N=F*D
## cross layer
x = x0
for i in range(num_cross_layers):
x = cross_layer2(x0, x, 'cross_{}'.format(i))
cross_layer = x
## deep layer
net = x0
for units in hidden_size_lst:
net = tf.layers.dense(net, units=units, activation=tf.nn.relu)
deep_layer = net
out = tf.concat([cross_layer, deep_layer], 1)
say something:
在cross_layer实现的时候,先计算了结果为标量的\(x_l^Tw\),而非按照公式从左到右计算,主要是考虑到临时存储内存空间的大小,\(x_0x_l^T\)这一个操作需要的内存就是\(batch\_size*(filed*dim)*(filed*dim)*(4or8)\),这仅仅是一层的操作,矩阵与向量相乘也是非常消耗计算资源的,在企业场景中这是难以接受的(\(if\quad filed*dim=1k, batch=1k, float, one\_layer\_memory=4G\)),因此利用矩阵乘法的结合律,先计算\(x_l^Tw\)得到标量,几乎不占存储空间,再与权重向量相乘。
这多说一句性能,可能在离线实验时并没有关注模型性能问题,主要以实现功能为主,但后期有效果需要上线时就要考虑代码实现方式的问题了,曾经有一次架构人员忙了半个月才优化下去20%的耗时,我从模型代码实现方式这块优化50%的耗时,并不是后者多牛逼(毕竟最初版本的烂代码也是自己写的),只是大家站在不同的角度去解决问题,很多时候性能问题在离线验证中是最容易被忽略的。
xDeepFM: eXtreme Deep Factorization Machine, 2018
出发点:解决DCN的输出被限制在特征形式上,与DeepFM相比和DCN是近亲;
优点:同时学习到显示的高阶特征交叉(CIN)与隐式的高阶特征交叉(DNN);在交叉特征CIN的学习上采用vector-wise的交叉;
缺点:CIN的时间复杂度较高;CIN的sum pooling会损失信息;
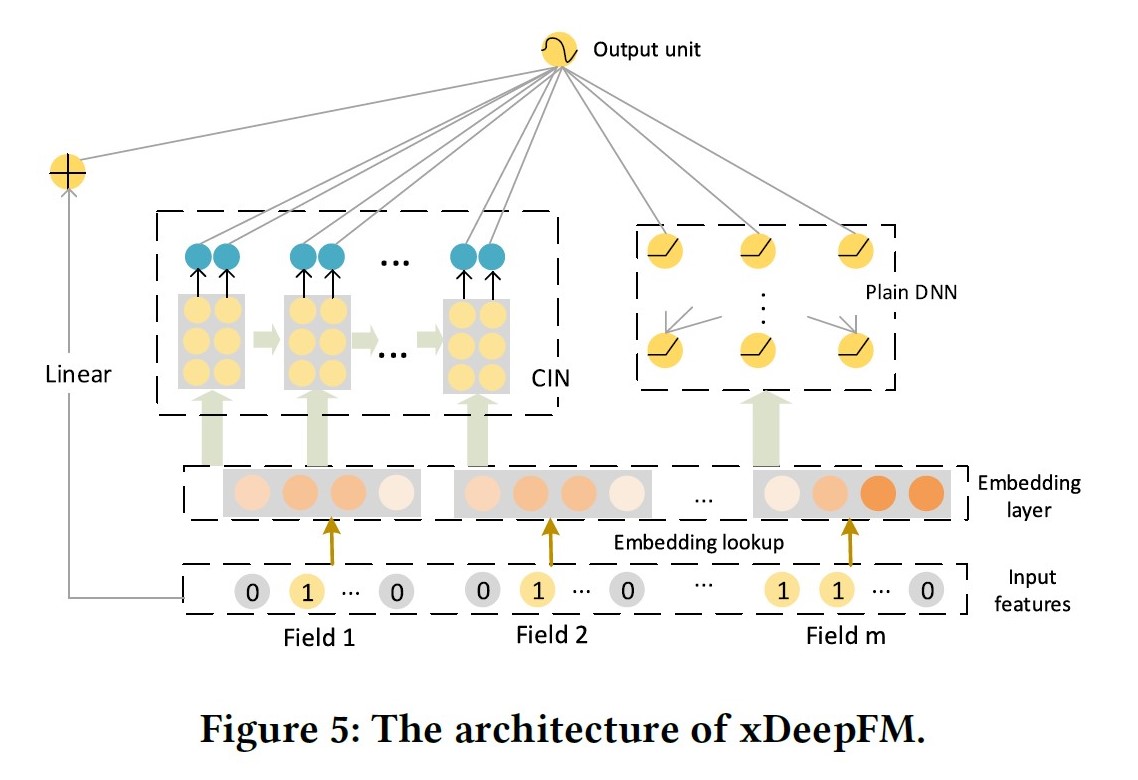
模型分为三部分:
- Linear Part: 捕获线性特征;
- DNN Part: 隐式的、bit-wise的学习高阶交叉特征;
- CIN Part: 压缩交互网络,显示的、vector-wise的学习高阶交叉特征;
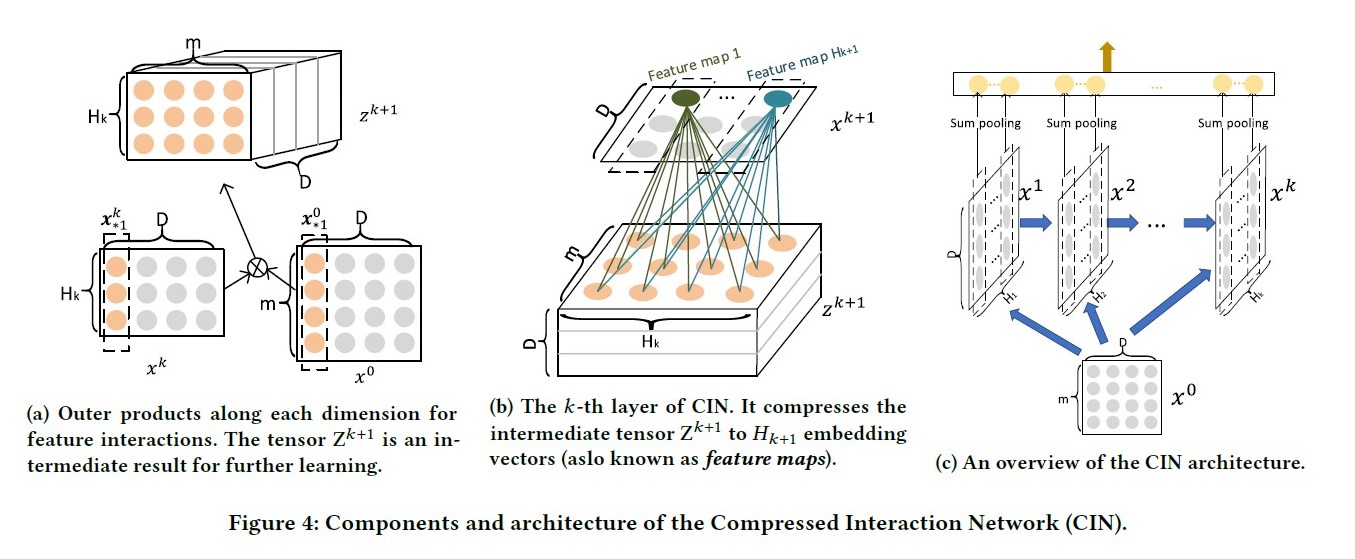
CIN结构:
令\(X^k\in R^{H_k\*D}\)表示第\(k\)层的输出,其中\(H_k\)表示第\(k\)层的vector个数,vecor维度始终为\(D\) ,保持和输入层一致。具体地,第\(k\)层每个vector的计算方式为:
其中W^{k,h}表示第\(k\)层的第\(h\)个vector的权重矩阵, \(\circ\)表示Hadamard乘积,即逐元素乘,例如\(<a1,b1,c1>\circ <a2,b2,c2>=<a1*a2,b1*b2,c1*c2>\)。
取前一层\(X^{k-1}\in R^{H_{k-1}*D}\)中的\(H_{k-1}\)个vector,与输入层\(X^0\in R^{m*D}\)中的m个vector,进行两两Hadamard乘积(外积)运算,得到\(H_{k-1}*m\)个vector,然后加权求和。
第k层的不同vector区别在于,对这\(H_{k-1}*m\)个vector求和的权重矩阵不同。权重\(W^{k,i}\in R^{H_{k-1}*m}顺着tensor维度D逐层相乘相加,得到k层第i个向量,\)H_k\(即对应有多少个不同的权重矩阵\)W^k$ , 是一个可以调整的超参。
将外积结果看成是三维矩阵\(m*H_k*D\),不同权重在维度D方向上加权求和,可看作是在\(m*H_k\)整个平面上的卷积操作。
def _build_extreme_FM(hparams, nn_input, field_num, dim, cross_layer_sizes):
hidden_nn_layers = []
field_nums = []
final_len = 0
nn_input = tf.reshape(nn_input, shape=[-1, field_num, dim]) # shape=(B F0 D)
field_nums.append(field_num)
hidden_nn_layers.append(nn_input)
final_result = []
split_tensor0 = tf.split(hidden_nn_layers[0], dim * [1], 2) # [shape=(B F0 1)]*D
with tf.variable_scope("exfm_part", initializer=self.initializer) as scope:
for idx, layer_size in enumerate(cross_layer_sizes):
split_tensor = tf.split(hidden_nn_layers[-1], dim * [1], 2) # [shape=(B Fi 1)]*D
dot_result_m = tf.matmul(split_tensor0, split_tensor, transpose_b=True) # shape=(D B F0 Fi)
dot_result_o = tf.reshape(dot_result_m, shape=[dim, -1, field_nums[0]*field_nums[-1]])
dot_result = tf.transpose(dot_result_o, perm=[1, 0, 2]) # shape=(B D F0*Fi)
filters = tf.get_variable(name="f_"+str(idx),
shape=[1, field_nums[-1]*field_nums[0], layer_size], # shape=(1 F0*Fi F{i+1})
dtype=tf.float32)
curr_out = tf.nn.conv1d(dot_result, filters=filters, stride=1, padding='VALID') # shape=(B D F{i+1})
curr_out = tf.nn.relu(curr_out)
curr_out = tf.transpose(curr_out, perm=[0, 2, 1]) # shape=(B Fi+1 D)
direct_connect = curr_out
next_hidden = curr_out
final_len += layer_size
field_nums.append(int(layer_size))
final_result.append(direct_connect)
hidden_nn_layers.append(next_hidden)
result = tf.concat(final_result, axis=1)
result = tf.reduce_sum(result, -1)
w_nn_output = tf.get_variable(name='w_nn_output',
shape=[final_len, 1],
dtype=tf.float32)
b_nn_output = tf.get_variable(name='b_nn_output',
shape=[1],
dtype=tf.float32,
initializer=tf.zeros_initializer())
exFM_out = tf.nn.xw_plus_b(result, w_nn_output, b_nn_output)
return exFM_out
say something:
如果CIN只有一层,\(H_1=m, W^1=1\),则sum pooling的输出结果就是一系列两两向量内积之和,是标准FM。
复杂度分析,假设CIN和DNN每层向量/神经元个数都为H,网络深度为T。CIN的参数空间复杂度为\(O(mTH^2)\) ,普通的DNN为\(O(mDH+TH^2)\),CIN的空间复杂度与输入维度D无关。CIN的时间复杂度为\(O(mH^2DT)\) ,而DNN为\(O(mDH+TH^2)\),时间复杂度会是CIN的一个主要痛点。
DCN的残差项保证了特征的1~l+1特征都有,而CIN中去除了残差项,虽然更快了,但是相当于丢弃了1~l阶特征的组合结果。
AutoInt: Automatic Feature Interaction Learning
出发点:使用multi-head self attention(Transformer里的那个) 机制来进行自动特征交叉学习,以提升CTR预测任务的精度;
优点:可显示的以vector-wise的方式学习有限阶特征交叉信息;
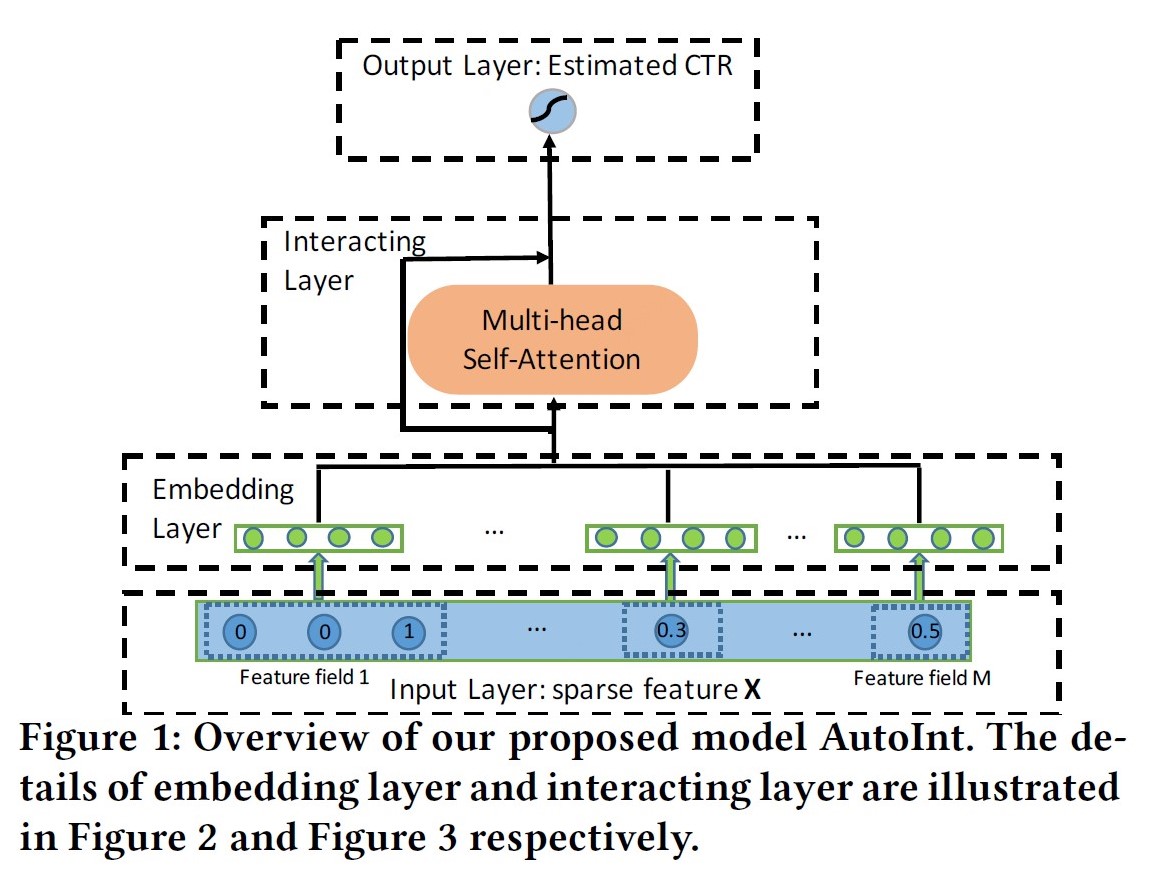
模型:
AutoInt直接采用了单路的模型结构,将原始特征embedding后直接进行Self-attention操作,将输入与输出连接做残差ResNet,多层堆叠后输出。论文中给出了AutoInt+DNN的双路模型实验AutoInt+。
文章里拆分的公式看着太费劲,还是Transformer里的刚易懂。
def multihead_attention(queries, keys, values,
num_units=None,
num_heads=1,
dropout_keep_prob=1,
is_training=True,
has_residual=True):
if num_units is None:
num_units = queries.get_shape().as_list[-1]
# Linear projections
Q = tf.layers.dense(queries, num_units, activation=tf.nn.relu)
K = tf.layers.dense(keys, num_units, activation=tf.nn.relu)
V = tf.layers.dense(values, num_units, activation=tf.nn.relu)
Q_ = tf.concat(tf.split(Q, num_heads, axis=2), axis=0)
K_ = tf.concat(tf.split(K, num_heads, axis=2), axis=0)
V_ = tf.concat(tf.split(V, num_heads, axis=2), axis=0)
QK = tf.matmul(Q_, tf.transpose(K_, [0, 2, 1]))
weights = QK / (K_.get_shape().as_list()[-1] ** 0.5)
weights = tf.nn.softmax(weights)
weights = tf.layers.dropout(weights, rate=1-dropout_keep_prob,
training=tf.convert_to_tensor(is_training))
# Weighted sum
outputs = tf.matmul(weights, V_)
# Restore shape
outputs = tf.concat(tf.split(outputs, num_heads, axis=0), axis=2)
# Residual connection
if has_residual:
V_res = tf.layers.dense(values, num_units, activation=tf.nn.relu)
outputs += V_res
outputs = tf.nn.relu(outputs)
# Normalize
outputs = normalize(outputs)
return outputs
def AutoInt(x_id, feature_size, dim, blocks):
field_size = x_id.get_shape().as_list()[1]
embemdding_matrix = tf.Variable(tf.random_uniform([feature_size, dim], -0.1, 0.1), dtype=tf.float32)
emb_vec = tf.nn.embedding_lookup(embemdding_matrix, x_id) # Batch*field*Dim (B,F,D)
for i in range(blocks):
emb_vec = multihead_attention(queries=emb_vec, keys=emb_vec, values=emb_vec)
flat = tf.reshape(emb_vec, shape=[-1, dim * field_size])
out = tf.layers.dense(flat, 1, activation=None)
say something:
如果看过"Attenion is all you need"论文的话,这个工作很快就能看完并理解,连作者开源的代码都是直接从Transformer的gitcode中扒下来的。工作虽然是已有知识迁移到ctr领域,但仍是很好的创新,模型结构清晰简洁。
墙裂案例https://www.github.com/kyubyong/transformer 这个代码。
Reference
overview:
https://blog.csdn.net/han_xiaoyang/article/details/81031961
https://zhuanlan.zhihu.com/p/104307718
PNN: https://zhuanlan.zhihu.com/p/56651241
ONN: https://cloud.tencent.com/developer/news/456076
DCN: http://xudongyang.coding.me/dcn/
ffm: https://tech.meituan.com/2016/03/03/deep-understanding-of-ffm-principles-and-practices.html
autoint: https://zhuanlan.zhihu.com/p/60185134
xdeepFM:
https://www.jianshu.com/p/b4128bc79df0
http://www.shataowei.com/2019/12/17/xDeepFM架构理解及实现/
http://xudongyang.coding.me/xdeepfm/
https://zhuanlan.zhihu.com/p/57162373
https://blog.csdn.net/DaVinciL/article/details/81359245

