程序猿修仙之路--算法之希尔排序

     

           

           

IT

江

湖          

       自冯诺依曼开启大计算机时代以来，经过近一个世纪的蓬勃发展，已然成为一个人才众多的群体：IT江湖            

        依附市场规律，江湖上悄然兴起数十宗门，其中以AI，大数据近期最为热门。每个宗门人才济济，抢夺人才大战早已在阿里，腾讯，百度等数百个国度白热化。            

      IT江湖人士凭借JAVA，Python等武器，在精通各路内功心法的基础上在各个国度扬名立万，修仙成佛者众多，为后人树下追宠之榜样。            

    内功心法众多，其中以算法最为精妙，是修仙德道必经之路。            

       

               

虽然江湖上算法内功繁多，但是好的算法小编认为必须符合以下几个条件，方能真正提高习练者实力：

1            

时间复杂度（运行时间）        

       在算法时间复杂度维度，我们主要对比较和交换的次数做对比，其他不交换元素的算法，主要会以访问数组的次数的维度做对比。。            

        其实有很多修炼者对于算法的时间复杂度有点模糊，分不清什么所谓的 O(n),O(nlogn),O(logn)...等，也许下图对一些人有一些更直观的认识。   

2            

空间复杂度（额外的内存使用）        

    排序算法的额外内存开销和运行时间同等重要。 就算一个算法时间复杂度比较优秀，空间复杂度非常差，使用的额外内存非常大，菜菜认为它也算不上一个优秀的算法。

3            

结果的正确性        

    这个指标是菜菜自己加上的，我始终认为一个优秀的算法最终得到的结果必须是正确的。就算一个算法拥有非常优秀的时间和空间复杂度，但是结果不正确，导致修炼者经脉逆转，走火入魔，又有什么意义呢？
           

   

               

    算法虽然精妙，但需循序渐进修炼，并且需要一定的数学内功基础方可彻底领悟。今日习练算法第三章：排序之希尔排序。

           

心法简介    

    上一篇我们修炼了插入排序，希尔排序（又名Shell's Sort）本质上属于插入排序，是插入排序的一种更高效升级版本，也称为**缩小增量排序**。同时希尔排序在时间复杂度上也是突破O(n²）的第一批算法之一。你说厉不厉害？~~            

心法基本思想    

        通过直接插入排序的修炼，我们知道直接插入排序是一种性能比较低的初级算法，对修炼者提升不是不大， 但是有一点优势那就是对于小型数组或者部分有序的数组非常高效，希尔排序就是基于这一点优势对直接插入排序进行了改良。换句话说直接插入排序低效的原因在于无序，无序的程度越高越低效。例如：最小的元素初始位置在数组的另一端，此元素要想到达正确位置，是需要一个一个位置前移，最终需要N-1次移动。如何改变这种状态正是希尔排序的突破口。    

        希尔排序的思想是把数组下标按照一定的增量h分组，然后对每组进行直接插入排序。在进行排序时，如果h很大，我们就能将元素移动到很远的地方，为实现更小的h有序创造方便。然后增量h逐渐减小（每个分组的元素量增多），直到h为1整个数组划分为一组，排序结束。    

        也许一张更直观的图比上千句话效果都好    

           

               

   

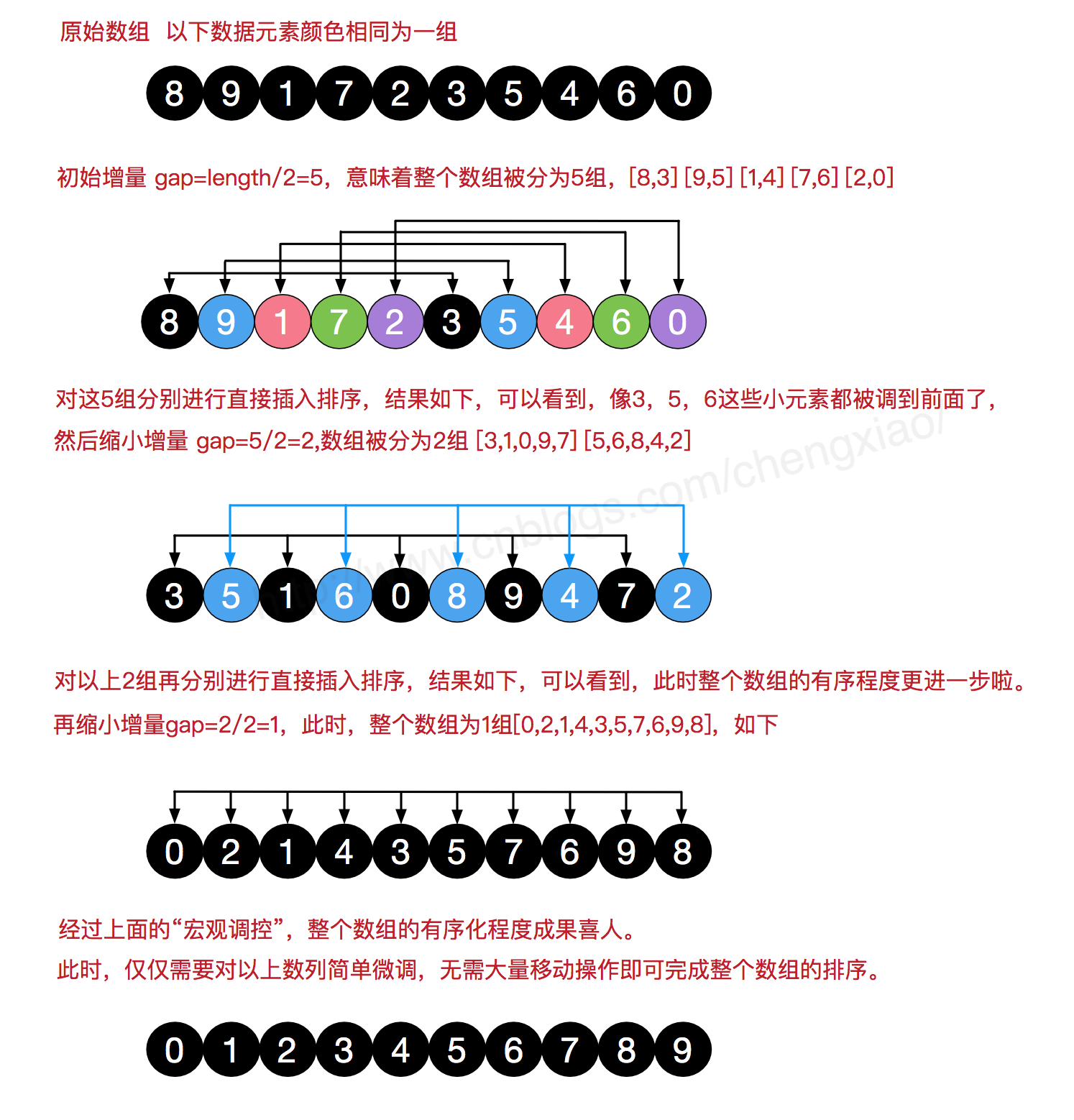
心法复杂度  

 

    时间复杂度

1. 最坏时间复杂度依然为O(n²)，一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为O(n^3/2)，最好情况下为O(n)属于线性复杂度。                 

2. 空间复杂度

   优于希尔排序本质上属于插入排序升级版，所以空间上和直接插入排序一致为O(1)，在常数级别。       

性能和特点       

1. 希尔排序之所以高效是因为它权衡了子数组的规模和有序性。排序之初各个子数组都很短，这种情况很适合插入排序.             

对于增量h的选择对希尔排序非常重要，直接影响其性能。其实除了h的选择之外，h之间的数学性质也影响希尔排序的性能，比如它们的公因子等。很多论文研究了各种不同的递增续列但都无法证明某个序列是最好的。对于某些基础递增的序列其实在性能上和某些复杂的序列接近，所以很多情况下我们没有必要花大力气在复杂序列上的研究上。        

 

适用场景

        与插入排序不同，希尔排序可以适用于大型数组，它对任意排序的数组表现良好，虽然不是最好。实验证明，希尔排序比我们上两章学习的选择排序和插入排序要快的多，并且数组越大，优势越大。目前最重要的结论是：希尔排序的运行时间达不到平方级别。

        对于中等大小的数组希尔排序的时间是在可接受范围之内的，因为它的代码量很小，而且需要的额外空间很小，几乎可以忽略。对于其他更高效的其他算法，可能比希尔排序更高效，但是代码也更复杂，性能上比希尔排序也高不了几倍，所以在很多情况下希尔排序成为首选的算法。

 

其他      

1. 直接插入排序是稳定的，希尔排序呢？   

由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以希尔排序排序是不稳定的。    

   

   

            

1                                

c#武器版本            

static void Main(string[] args)
        { 
             List<int> data = new List<int>() ;
            for (int i = 0; i < 11; i++)
           {                
               data.Add(new Random(Guid.NewGuid().GetHashCode()).Next(1, 100));
           }
           //打印原始数组值
           Console.WriteLine($"原始数据： {string.Join(",", data)}");
           int n = data.Count;
           int h = 1;
           //计算初始化增量，网络提供，据说比较好的递增因子
           while (h < n / 3)
           {
               h = 3 * h + 1;
            }
            Console.WriteLine($"初始化增量：{h}");
            while (h >= 1)
           {
               for (int i = h; i < n; i++)
               {
                   for (int j = i; j >=h&&data[j]<data[j-h]; j-=h)
                   {
                       //异或法 交换两个变量，不用临时变量
                       data[j] = data[j] ^ data[j - 1];
                       data[j - 1] = data[j] ^ data[j - 1];
                       data[j] = data[j] ^ data[j - 1];
                   }
               }
               h = h / 3;
           }
           //打印排序后的数组
           Console.WriteLine($"排序数据： {string.Join(",", data)}");            Console.Read();
       }

运行结果：

原始数据： 47,50,32,42,44,79,10,16,51,74,52

初始化增量：4

排序数据： 10,16,32,42,44,47,50,51,52,74,79

2                                

golang武器版本 

package main
import (	
        "fmt"
	"math/rand"
)

func main() {	
    var data []int	
    for i := 0; i < 11; i++ {		
        data = append(data, rand.Intn(100))
    }
    fmt.Println(data)	
        var n = len(data)	
        var h = 1
	for h < n/3 {
	    h = 3*h + 1
	}
	fmt.Println(h)	
        for h >= 1 {		
            for i := h; i < n; i++ {			
                for j := i; j >= h && data[j] < data[j-h]; j -= h {				
                    data[j], data[j-h] = data[j-h], data[j]
		}
	    }
	    h = h / 3
	}
	fmt.Println(data)
}

运行结果：

[81 87 47 59 81 18 25 40 56 0 94]

4

[0 18 25 40 47 56 59 81 81 87 94]

菜鸟奋斗史出品

见证菜鸟的成长之路