P3376 【模板】网络最大流
题目描述:
题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入格式
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入 #1
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
输出 #1
50
说明/提示
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明:
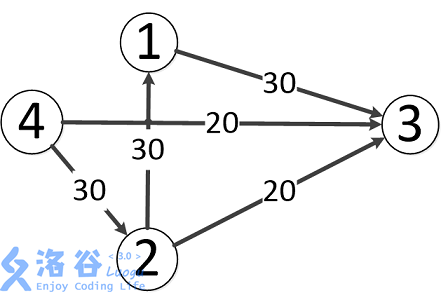
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
思路:
网络流模板题,再次试验了基于链式前向星的带有当前弧优化的Dinic算法
注意cnt开始取1,有效从2开始,这是为了配合以后的e[i^1]运算找到相反边。
比如:2(10)->3(11)
如果是从1开始:1->0就不能找到相反边(WA了好多次QWQ)
#include <iostream>
#include <memory.h>
#include <queue>
#define INF 0x3f3f3f3f
#define max_n 200005
using namespace std;
int n,m;
int s,t;
int flag;
int max_flow = 0;
int head[max_n];
int cnt = 1;
struct edge
{
int v;
int nxt;
int w;
}e[max_n<<1];
void add(int u,int v,int w)
{
++cnt;
e[cnt].v = v;
e[cnt].w = w;
e[cnt].nxt = head[u];
head[u] = cnt;
}
int instack[max_n];
int depth[max_n];
int cur[max_n];
int BFS()
{
//memset(depth,INF,sizeof(depth));
//memset(instack,0,sizeof(instack));
for(int i = 0;i<=n;i++)
{
cur[i] = head[i];depth[i] = INF;instack[i] = 0;
}
depth[s] = 0;
queue<int> que;
que.push(s);
instack[s] = 1;
while(!que.empty())
{
int u = que.front();
instack[u] = 0;
que.pop();
for(int i = head[u];i;i=e[i].nxt)
{
int v = e[i].v;
if(depth[v]>depth[u]+1&&e[i].w>0)
{
depth[v] = depth[u]+1;
if(instack[v]==0)
{
que.push(v);
instack[v] = 1;
}
}
}
}
if(depth[t]!=INF) return 1;
return 0;
}
int DFS(int u,int low)
{
int rlow = 0;
if(u==t)
{
flag=1;
max_flow += low;
return low;
}
int used = 0;
for(int i = cur[u];i;i=e[i].nxt)
{
cur[u] = i;
int v = e[i].v;
if(e[i].w>0&&depth[v]==depth[u]+1)
{
if(rlow=DFS(v,min(low-used,e[i].w)))
{
used += rlow;
e[i].w -= rlow;
e[i^1].w += rlow;
if(used==low) break;
}
}
}
return used;
}
int Dinic()
{
while(BFS())
{
flag=1;
while(flag==1)
{
flag = 0;
DFS(s,INF);
}
}
return max_flow;
}
int main()
{
cin >> n >> m >> s >> t;
for(int i = 1;i<=m;i++)
{
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
add(b,a,0);
}
cout << Dinic() << endl;
return 0;
}
就是这样
我们不只生产博客,也是优质博客链接的搬运工


