竞赛197

仅含 1 的子串数

 

给你一个二进制字符串 s（仅由 '0' 和 '1' 组成的字符串）。

返回所有字符都为 1 的子字符串的数目。

由于答案可能很大，请你将它对 10^9 + 7 取模后返回。

 

示例 1：

输入：s = "0110111"
输出：9
解释：共有 9 个子字符串仅由 '1' 组成
"1" -> 5 次
"11" -> 3 次
"111" -> 1 次
示例 2：

输入：s = "101"
输出：2
解释：子字符串 "1" 在 s 中共出现 2 次
示例 3：

输入：s = "111111"
输出：21
解释：每个子字符串都仅由 '1' 组成
示例 4：

输入：s = "000"
输出：0
 

提示：

s[i] == '0' 或 s[i] == '1'
1 <= s.length <= 10^5

/**
 * @param {string} s
 * @return {number}
 */
var numSub = function(s) {
    // let len = s.length;
    let arr = s.split('0').filter(f=>f)
    let r = 0;
    arr.forEach(a=>{
        let len = a.length;
        r+=len*(1+len)/2
        r = r%(10**9+7)
        // for(let i=0; i<len; i++){
        //     for(let j=i+1; j<=len; j++){
        //         // let sub = s.slice(i, j)
        //         // console.log(sub)
        //         // if(sub.indexOf('0')>=0){
        //             // continue
        //         // } else {
        //             r = r%(10**9+7)
        //             r++
        //         // }
        //     }
        // }
    })
    
    return r
    
};

　总结：最后差点没做出了，提高200名次，偶然间百度出有这么个规律。

双层for循环不管怎么整，都会有测试用例不通过。规律就是

“1” 的子串数是： 1*(1+1)/2

"11" 的子串数是：2*(1+2)/2

"111"的子串数是： 3*(1+3)/2

....

所以关系式是个等差数列公式

 这个是简单题，还有一个中等题，当时花了1个多小时也没弄出来，丢掉了前200名的机会。就是“统计全是1能组成的矩形”，

参考连接：https://www.cnblogs.com/zhangzs000/p/13293009.html  “

统计全 1 子矩形

”

概率最大的路径

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

 

示例 1：

 

 

 

输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25
示例 2：

 

 

 

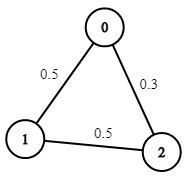
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000
示例 3：

 

 

 

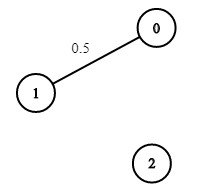
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径
 

提示：

2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边

 

/**
 * @param {number} n
 * @param {number[][]} edges
 * @param {number[]} succProb
 * @param {number} start
 * @param {number} end
 * @return {number}
 */
// 同样是优先队列的方法，JavaScript却超时，c++却不会，这就是JavaScript的弊端了，思路一样都不一定能过
var maxProbability = function(n, edges, succProb, start, end) {
    let vi = new Array(n).fill(false);
    let path = new Array(n)
    while(n--){
        path[n] = []
    }
    for (let i = 0; i < edges.length; i++) {
        let e = edges[i];
        path[e[0]].push([succProb[i], e[1]]);
        path[e[1]].push([succProb[i], e[0]]);
    }
    let pq = [];
    pq.push([ 1, start]);
    while (pq.length) {
        let [curProb, cur] = pq.shift()// pq.pop(); pop是操作数组的后边
        if (vi[cur]) continue;
        vi[cur] = true;

        if (cur == end) return curProb;
        let pp =path[cur];
        for(let i=0; i<pp.length; i++){
            let [nextProb, next] = pp[i];
            if (vi[next]) continue;
            pq.push([curProb * nextProb, next]);
            pq.sort((a, b)=>b[0]-a[0])  
        }
    }

    return 0;
};

　总结：

不管它图是怎么样连的，优先队列决定了它的行走路线始终都是沿着概率最大的方向行走，并且用vi这个数组就决定了它下一步决定不会倒回去走，这样逐步逼近终点。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-substrings-with-only-1s
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。