179竞赛
灯泡开关 III
房间中有 n 枚灯泡,编号从 1 到 n,自左向右排成一排。最初,所有的灯都是关着的。
在 k 时刻( k 的取值范围是 0 到 n - 1),我们打开 light[k] 这个灯。
灯的颜色要想 变成蓝色 就必须同时满足下面两个条件:
灯处于打开状态。
排在它之前(左侧)的所有灯也都处于打开状态。
请返回能够让 所有开着的 灯都 变成蓝色 的时刻 数目 。
示例 1:
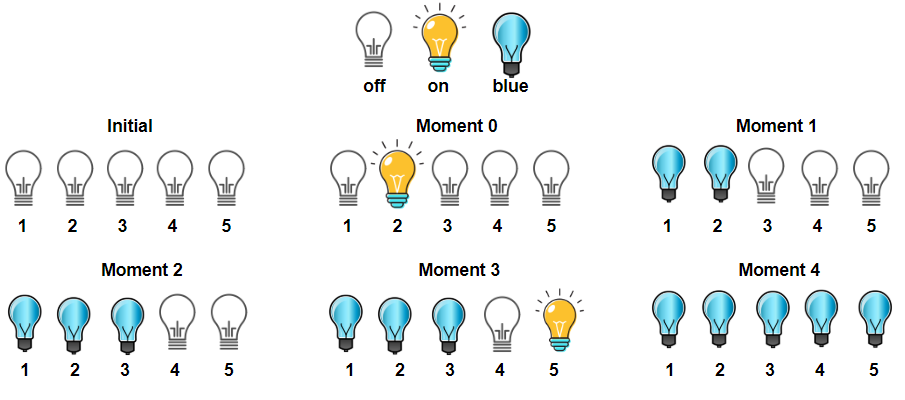
输入:light = [2,1,3,5,4]
输出:3
解释:所有开着的灯都变蓝的时刻分别是 1,2 和 4 。
示例 2:
输入:light = [3,2,4,1,5]
输出:2
解释:所有开着的灯都变蓝的时刻分别是 3 和 4(index-0)。
示例 3:
输入:light = [4,1,2,3]
输出:1
解释:所有开着的灯都变蓝的时刻是 3(index-0)。
第 4 个灯在时刻 3 变蓝。
示例 4:
输入:light = [2,1,4,3,6,5]
输出:3
示例 5:
输入:light = [1,2,3,4,5,6]
输出:6
提示:
n == light.length
1 <= n <= 5 * 10^4
light 是 [1, 2, ..., n] 的一个排列。
/**
* @param {number[]} light
* @return {number}
*/
// 亮灯的个数 == 当前亮灯的最大编号
var numTimesAllBlue = function(light) {
let m =1, cnt =0;
for(let i=0;i<light.length;i++){
m=Math.max(light[i],m);
// 亮灯的个数 = i+1
// m 当前亮灯的最大编号
if(m==i+1)
cnt++;
}
return cnt;
};
/*
// 参观过的标记为true, 什么时候能一顺溜的都是true且 === 亮灯的最大编号
var numTimesAllBlue = function(light) {
let cur = 0, ans = 0, maxi = 0;
let vis = new Array(50000);
light.forEach(x=>{
vis[x] = true;
maxi = Math.max(maxi, x);
while (vis[cur + 1])
++cur;
if (cur == maxi) ++ans;
})
return ans
}
*/
/*
// 亮灯的个数 == 当前亮灯的最大编号
var numTimesAllBlue = function(light) {
let m =1, cnt =0;
for(let i=0;i<light.length;i++){
m=Math.max(light[i],m);
// 亮灯的个数 = i+1
// m 当前亮灯的最大编号
if(m==i+1)
cnt++;
}
return cnt;
};
*/
/**
* 这个当时竞赛的时候怎么搞都超时,关键还是在应用亮灯的最大编号。
// 当时最开始还以为只要左边连续就计数,后来一想还要右边连续,就写了个这,超时
var numTimesAllBlue = function(light) {
// let arr = [];
let res = 0;
let len = light.length;
let ls = new Array(len).fill(0);
let max = -1;
light.forEach((l, i)=>{
if(l-1 >max){
max = l-1
}
ls[l-1] = 1
let flag = true;
let sub = ls.slice(0, l-1);
let sub1 = ls.slice(l-1, max);
// console.log(sub)
if(sub.some(s=>s!==1) || sub1.some(e=>e!==1)){
flag = false;
}
if(flag){
// arr.push(i)
res++
}
// console.log(arr, '----')
})
return res;
};
*/
通知所有员工所需的时间
公司里有 n 名员工,每个员工的 ID 都是独一无二的,编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。
在 manager 数组中,每个员工都有一个直属负责人,其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人,manager[headID] = -1。题目保证从属关系可以用树结构显示。
公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们,然后由这些下属通知他们的下属,直到所有的员工都得知这条紧急消息。
第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属(也就是说在 informTime[i] 分钟后,他的所有直属下属都可以开始传播这一消息)。
返回通知所有员工这一紧急消息所需要的 分钟数 。
示例 1:
输入:n = 1, headID = 0, manager = [-1], informTime = [0]
输出:0
解释:公司总负责人是该公司的唯一一名员工。
示例 2:
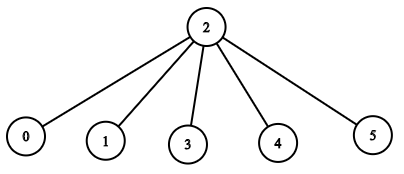
输入:n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
输出:1
解释:id = 2 的员工是公司的总负责人,也是其他所有员工的直属负责人,他需要 1 分钟来通知所有员工。
上图显示了公司员工的树结构。
示例 3:
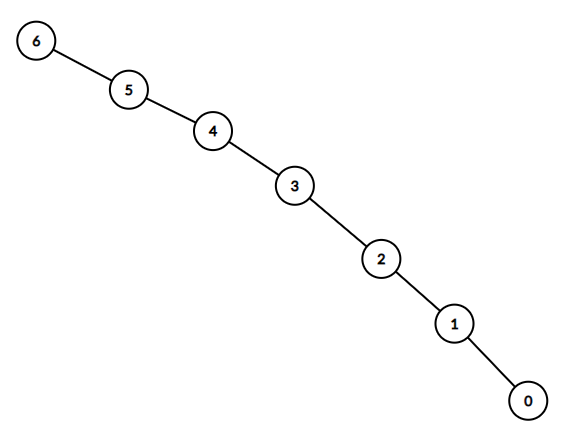
输入:n = 7, headID = 6, manager = [1,2,3,4,5,6,-1], informTime = [0,6,5,4,3,2,1]
输出:21
解释:总负责人 id = 6。他将在 1 分钟内通知 id = 5 的员工。
id = 5 的员工将在 2 分钟内通知 id = 4 的员工。
id = 4 的员工将在 3 分钟内通知 id = 3 的员工。
id = 3 的员工将在 4 分钟内通知 id = 2 的员工。
id = 2 的员工将在 5 分钟内通知 id = 1 的员工。
id = 1 的员工将在 6 分钟内通知 id = 0 的员工。
所需时间 = 1 + 2 + 3 + 4 + 5 + 6 = 21 。
示例 4:
输入:n = 15, headID = 0, manager = [-1,0,0,1,1,2,2,3,3,4,4,5,5,6,6], informTime = [1,1,1,1,1,1,1,0,0,0,0,0,0,0,0]
输出:3
解释:第一分钟总负责人通知员工 1 和 2 。
第二分钟他们将会通知员工 3, 4, 5 和 6 。
第三分钟他们将会通知剩下的员工。
示例 5:
输入:n = 4, headID = 2, manager = [3,3,-1,2], informTime = [0,0,162,914]
输出:1076
提示:
1 <= n <= 10^5
0 <= headID < n
manager.length == n
0 <= manager[i] < n
manager[headID] == -1
informTime.length == n
0 <= informTime[i] <= 1000
如果员工 i 没有下属,informTime[i] == 0 。
题目 保证 所有员工都可以收到通知。
/**
* @param {number} n
* @param {number} headID
* @param {number[]} manager
* @param {number[]} informTime
* @return {number}
*/
var numOfMinutes = function(n, headID, manager, informTime) {
const dfs = (arr, informTime, id, time, obj)=>{
time += informTime[id];
console.log(obj, id, time)
if (!arr[id].length){
// console.log(ans, time, '---')
obj.ans = Math.max(obj.ans, time);
return;
}
arr[id].forEach(subId=>{
dfs(arr, informTime, subId, time, obj);
})
}
let arr = new Array(manager.length);
for(let i=0;i<arr.length; i++){arr[i]= []};
for (let i = 0; i < manager.length; i++)
{
if (manager[i] == -1) continue;
arr[manager[i]].push(i);
}
// console.log('arr: ',arr)
let obj = {
ans: 0
}
dfs(arr, informTime, headID, 0, obj);
return obj.ans
};
/*
var numOfMinutes = function(n, headID, manager, informTime) {
const getChildren = (node)=>{
let val = node.val;
let gId = manager.indexOf(val);
let arr = [];
if(gId>-1){
for(let i=0; i<manager.length; i++){
if(manager[i]===val){
arr.push(i)
}
}
let childrens = []
arr.forEach(f=>{
let node = {
val: f,
childrens: null
}
childrens.push(node)
})
// console.log('node: ',node, ' childrens: ',childrens)
node.childrens = childrens
for(let j=0; j<childrens.length; j++){
// 失败1. 本来就是通过引用要给node添加属性的,结果这样搞成了undefined
// childrens[i].childrens = getChildren(childrens[j]);
getChildren(childrens[j]);
}
}
}
const get=(id)=>{
let arr = [];
let node = {
val: id,
childrens: null
}
for(let i=0; i<manager.length; i++){
if(manager[i]===id){
arr.push(i)
}
}
let childrens = []
arr.forEach(f=>{
let node = {
val: f,
childrens: null
}
childrens.push(node)
})
node.childrens = childrens
for(let j=0; j<childrens.length; j++){
// 失败1. 本来就是通过引用要给node添加属性的,结果这样搞成了undefined
// childrens[i].childrens = getChildren(childrens[j]);
getChildren(childrens[j]);
}
return node;
}
let node = get(headID)
let res = informTime[headID];
const bfs = (node)=>{
let s = [];
s.push(node)
while(s.length){
let len = s.length;
let t = -1;
for(let i=0; i<len; i++){
let n = s.shift();
if(n.childrens){
let childrens = n.childrens;
// console.log('childrens: ',childrens)
for(let j=0; j<childrens.length; j++){
t = Math.max(informTime[childrens[j].val], t)
s.push(childrens[j])
}
}
}
if(t!==-1) res+=t
// 失败2. bfs 每一层的节点个数,才能统计一次最大的耗时
// let n = s.shift();
// if(n.childrens){
// let childrens = n.childrens;
// let t = -1;
// // console.log('childrens: ',childrens)
// for(let j=0; j<childrens.length; j++){
// t = Math.max(informTime[childrens[j].val], t)
// s.push(childrens[j])
// }
// if(t!==-1)
// res+=t
// }
// 失败3. 有一种可能连续n(n>=2)层通知,总时间100, 都没有最初1层通知的时间大 999,按照我们的方式 999 + ....
// 所以应该是dfs,最大的一条,但这又怎么做呢。
}
}
bfs(node);
return res
};
*/
T 秒后青蛙的位置
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
青蛙无法跳回已经访问过的顶点。
如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述,其中 edges[i] = [fromi, toi] 意味着存在一条直接连通 fromi 和 toi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。
示例 1:

输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出:0.16666666666666666
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
示例 2:

输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出:0.3333333333333333
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。
示例 3:
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
输出:0.16666666666666666
提示:
1 <= n <= 100
edges.length == n-1
edges[i].length == 2
1 <= edges[i][0], edges[i][1] <= n
1 <= t <= 50
1 <= target <= n
与准确值误差在 10^-5 之内的结果将被判定为正确。
/**
* @param {number} n
* @param {number[][]} edges
* @param {number} t
* @param {number} target
* @return {number}
*/
var frogPosition = function(n, edges, t, target) {
function Node(i, pp, tt){
this.id=i;
this.p=pp;
this.t=tt;
}
let sets = [];
for(let i=0;i<=n;i++) sets[i]=[];
edges.forEach(e=>{
sets[e[0]].push(e[1]);
sets[e[1]].push(e[0]);
})
let q=[];
q.push(new Node(1,1.000000,0));
let vis=new Array(n+1).fill(false);
vis[1]=true;
while(q.length){
let u=q.shift();
if(u.t==t&&u.id==target){
return u.p;
}
let sz=0;
sets[u.id].forEach(nb=>{
if(!vis[nb]) sz++;
})
console.log(sz, u)
if(u.t<t){
let find=false;
for(let i=0, len = sets[u.id].length; i<len; i++){
let nb = sets[u.id][i];
if(vis[nb]) continue;
find=true;
vis[nb]=true;
q.push(new Node(nb,u.p/sz,u.t+1));
}
if(find==false){
q.push(new Node(u.id,u.p,u.t+1));
}
}
}
return 0.0;
}
/*
// 怎么处理最后层,t足够大在最后节点原地蹦
// 遍历到最后一层时,不断的push 最后一层的节点,直到 level 为 t
var frogPosition = function(n, edges, t, target) {
let arr = new Array(n+1);
for(let i=1; i<=n; i++){
arr[i] = [];
}
edges.forEach(e=>{
arr[e[0]].push(e[1])
})
let l1 = [], l2 = [];
const bfs = (init)=>{
let s = [];
s.push(init);
let level = 0;
while(s.length){
let len = s.length;
level++;
if(level>1){
l1.push(len)
}
console.log(s, level, l1, '------')
for(let i=0; i<len; i++) {
let n = s.shift();
let child = arr[n];
let clen = child.length;
l2.push(clen)
console.log(n, child, l2, '++++')
// if(level === t) {
// for(let j=0; j<clen; j++){
// if(child[j] === target){
// let r = 1;
// l1.forEach(l=>r*=(1/l))
// r*=(1/l2[l2.length-1])
// return r
// }
// }
// return 0
// } else if(level>t){
// return 0
// } else {
if(level<t){
if(clen) {
for(let j=0; j<clen; j++){
s.push(child[j])
}
} else {
// 影响计算概率
s.push(n)
}
} else if(level === t){
for(let j=0; j<clen; j++){
if(child[j] === target){
let r = 1;
l1.forEach(l=>r*=(1/l))
r*=(1/l2[l2.length-1])
return r
}
}
return 0
}
// }
}
}
}
return bfs(1)
};
*/
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/bulb-switcher-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。


