模拟信号的重建

用MATLAB实现余弦信号的采样恢复仿真。

clear all;clc;close all;
N=5;  %采样频率是fs=N=5，采样周期T=0.2
dianshu=N*N;
A=4;
f=2;
fai=1;
xcaichushi=0:N-1;
xlianchushi=0:0.1:N-1;
%先画一个前几个周期的
xn=0:dianshu-1;
xlian=0:0.1:dianshu-1;
ycai=A*sin(2*pi*f*(xcaichushi/N)+fai);  %ycai为采样序列
ylian=A*sin(2*pi*f*(xlianchushi/N)+fai);  %y为近似连续的函数
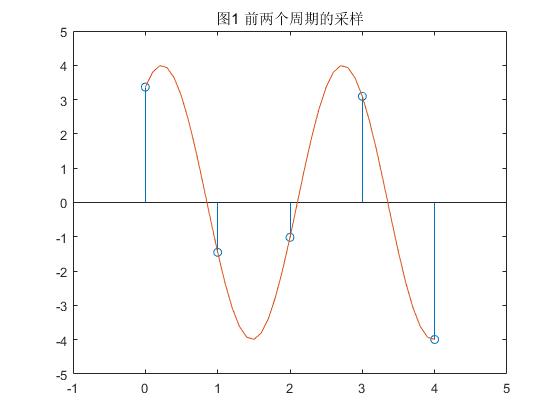
figure(1);
stem(xcaichushi,ycai);
hold on;
plot(xlianchushi,ylian); 
title('图1 前两个周期的采样');
axis([-1 5 -5 5]);
%前几个周期绘制完毕
for i=N+1:dianshu
    ycai(i)=ycai(i-5);
end
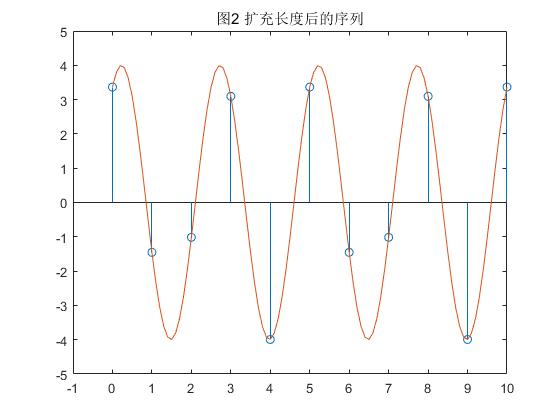
figure(2);
stem(xn,ycai);
for i=42:241
    ylian(i)=ylian(i-25);
end
hold on;
plot(xlian,ylian);
axis([-1,10,-5,5]);
title('图2 扩充长度后的序列');
%下面讨论加权抽样函数的相加
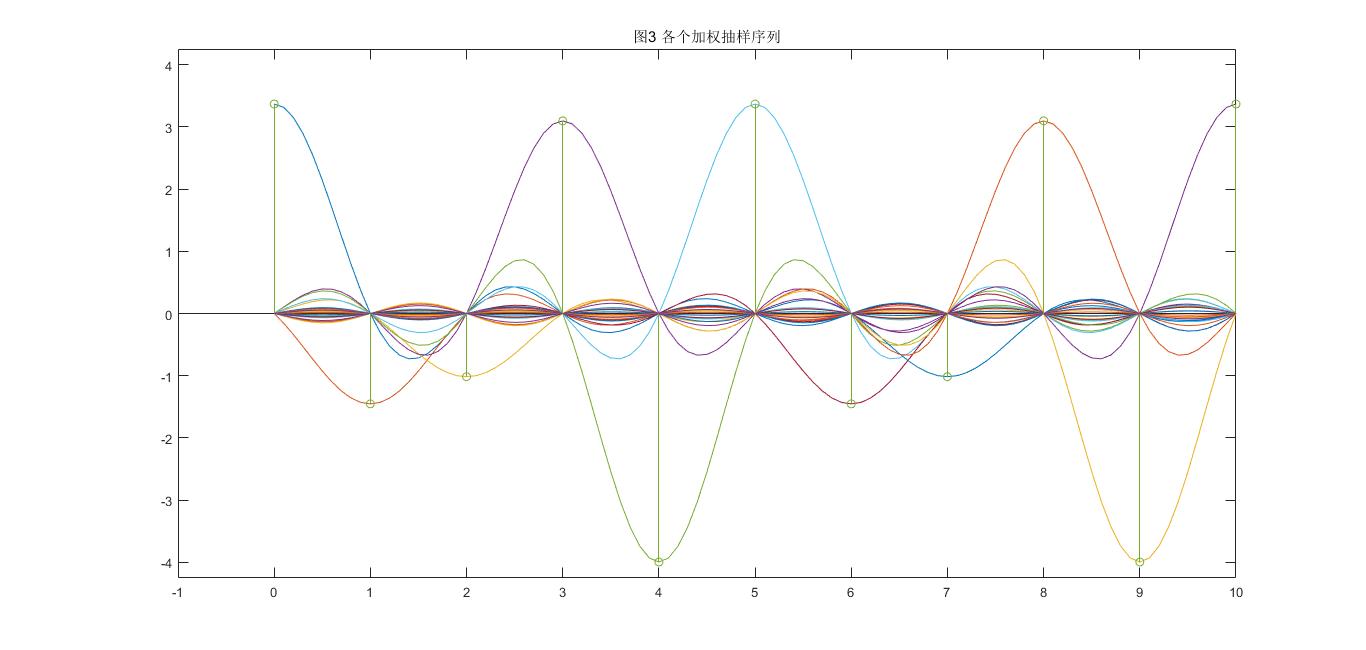
for j=1:N*N
    for i=1:length(xlian)
        saa(j,i)=ycai(j)*(sin(pi*(xlian(i)-(j-1)))./(pi*(xlian(i)-(j-1))));
    end
    %下面一行对整10+1点出现的，由sinx/x引起的NAN进行修正，具体怎样消除sinx/x出现NAN留待后面学习
    saa(j,10*j-9)=ycai(j);
    %修正完毕
    figure(3);
    plot(xlian,saa(j,:));
    hold on;
    title('图3 各个加权抽样序列');
    if j==1
        xjia=saa(j,:);
    else
        xjia=xjia+saa(j,:);
    end
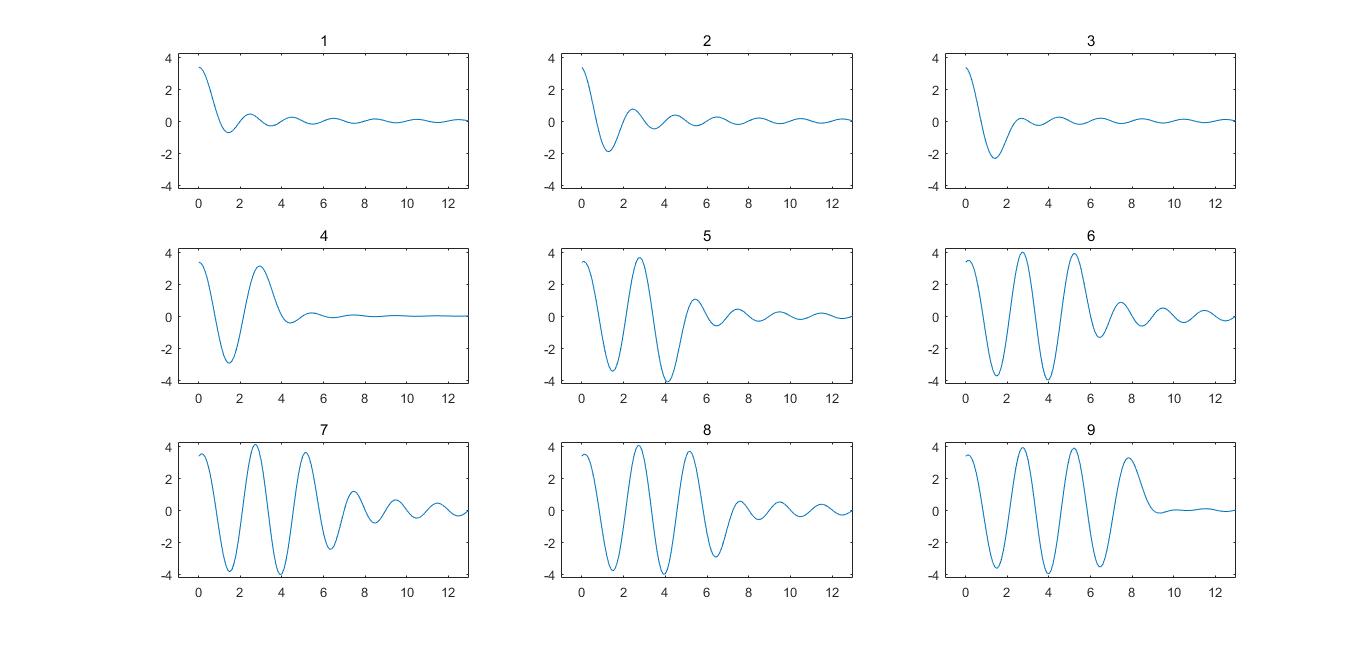
    if j<=9  %画出前1-9项加权抽样函数相加后的还原效果，对于周期函数而言，无穷多项方能完美还原，但考虑到抽样函数衰减很快，故有限多项可大致还原有限区间的函数样貌
        figure(4);
        subplot(3,3,j);
        plot(xlian,xjia);
        axis([-1 13 -A-0.25 A+0.25]);
        title([num2str(j)]);
    end
end
figure(3);
stem(xn,ycai);  %在采样加权序列上悬挂采样点，以直观观察加权抽样函数
axis([-1 10 -A-0.25 A+0.25]);

　　

4张结果图如下：

18.4.11补充：

傅里叶变换的对偶性：

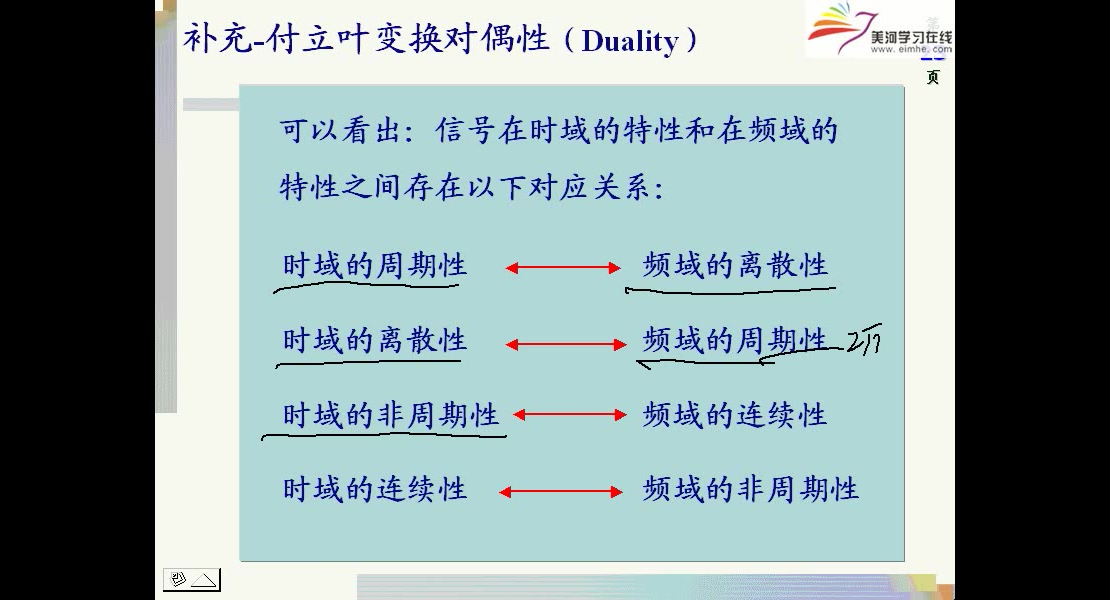
一个信号时域有限，频域就无限。时域有限等于某个信号（以它为一个周期进行周期延拓的信号）乘以一个时域矩形窗，频域等于该信号（频域是离散的）的频谱卷积上矩形窗的频谱，由于矩形窗的频谱是无限的，所以卷积后结果是无限的。

采样定理说的是时域无限信号（因为它要求信号是带限的），但是由于内插函数$\frac{{\sin \left[ {\frac{\pi }{T}(t - nT)} \right]}}{{\frac{\pi }{T}(t - nT)}}$有衰减效应，所以可用有限个采样点近似重建部分时域的信号。如图四第9张图片，通过9个采样点近似重建了前三个周期的信号。