Hacker's guide to Neural Networks - 3

 

from http://karpathy.github.io/neuralnets/

previous: https://www.cnblogs.com/zhangzhiwei122/p/15887306.html 

 

Recursive Case: Circuits with Multiple Gates

But hold on, you say: “The analytic gradient was trivial to derive for your super-simple expression. This is useless. What do I do when the expressions are much larger? Don’t the equations get huge and complex very fast?”. Good question. Yes the expressions get much more complex. No, this doesn’t make it much harder. As we will see, every gate will be hanging out by itself, completely unaware of any details of the huge and complex circuit that it could be part of. It will only worry about its inputs and it will compute its local derivatives as seen in the previous section, except now there will be a single extra multiplication it will have to do.

A single extra multiplication will turn a single (useless gate) into a cog in the complex machine that is an entire neural network.

I should stop hyping it up now. I hope I’ve piqued your interest! Lets drill down into details and get two gates involved with this next example:

 

 

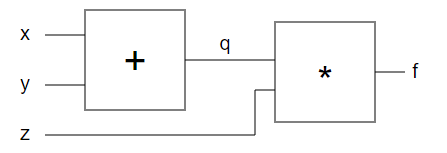
The expression we are computing now is f(x,y,z)=(x+y)zf(x,y,z)=(x+y)z. Lets structure the code as follows to make the gates explicit as functions:

var forwardMultiplyGate = function(a, b) { 
  return a * b;
};
var forwardAddGate = function(a, b) { 
  return a + b;
};
var forwardCircuit = function(x,y,z) { 
  var q = forwardAddGate(x, y);
  var f = forwardMultiplyGate(q, z);
  return f;
};

var x = -2, y = 5, z = -4;
var f = forwardCircuit(x, y, z); // output is -12

In the above, I am using a and b as the local variables in the gate functions so that we don’t get these confused with our circuit inputs x,y,z. As before, we are interested in finding the derivatives with respect to the three inputs x,y,z. But how do we compute it now that there are multiple gates involved? First, lets pretend that the + gate is not there and that we only have two variables in the circuit: q,z and a single * gate. Note that the q is is output of the + gate. If we don’t worry about x and y but only about q and z, then we are back to having only a single gate, and as far as that single * gate is concerned, we know what the (analytic) derivates are from previous section. We can write them down (except here we’re replacing x,y with q,z):

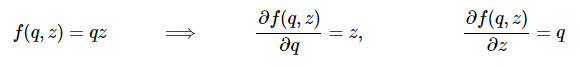
Simple enough: these are the expressions for the gradient with respect to q and z. But wait, we don’t want gradient with respect to q, but with respect to the inputs: x and y. Luckily, q is computed as a function of x and y (by addition in our example). We can write down the gradient for the addition gate as well, it’s even simpler:

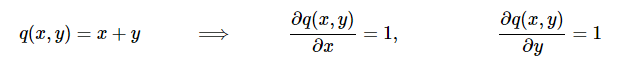
That’s right, the derivatives are just 1, regardless of the actual values of x and y. If you think about it, this makes sense because to make the output of a single addition gate higher, we expect a positive tug on both x and y, regardless of their values.

Backpropagation

We are finally ready to invoke the Chain Rule: We know how to compute the gradient of q with respect to x and y (that’s a single gate case with + as the gate). And we know how to compute the gradient of our final output with respect to q. The chain rule tells us how to combine these to get the gradient of the final output with respect to x and y, which is what we’re ultimately interested in. Best of all, the chain rule very simply states that the right thing to do is to simply multiply the gradients together to chain them. For example, the final derivative for x will be:

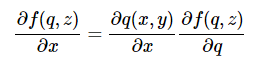
There are many symbols there so maybe this is confusing again, but it’s really just two numbers being multiplied together. Here is the code:

// initial conditions
var x = -2, y = 5, z = -4;
var q = forwardAddGate(x, y); // q is 3
var f = forwardMultiplyGate(q, z); // output is -12

// gradient of the MULTIPLY gate with respect to its inputs
// wrt is short for "with respect to"
var derivative_f_wrt_z = q; // 3
var derivative_f_wrt_q = z; // -4

// derivative of the ADD gate with respect to its inputs
var derivative_q_wrt_x = 1.0;
var derivative_q_wrt_y = 1.0;

// chain rule
var derivative_f_wrt_x = derivative_q_wrt_x * derivative_f_wrt_q; // -4
var derivative_f_wrt_y = derivative_q_wrt_y * derivative_f_wrt_q; // -4

That’s it. We computed the gradient (the forces) and now we can let our inputs respond to it by a bit. Lets add the gradients on top of the inputs. The output value of the circuit better increase, up from -12!

// final gradient, from above: [-4, -4, 3]
var gradient_f_wrt_xyz = [derivative_f_wrt_x, derivative_f_wrt_y, derivative_f_wrt_z]

// let the inputs respond to the force/tug:
var step_size = 0.01;
x = x + step_size * derivative_f_wrt_x; // -2.04
y = y + step_size * derivative_f_wrt_y; // 4.96
z = z + step_size * derivative_f_wrt_z; // -3.97

// Our circuit now better give higher output:
var q = forwardAddGate(x, y); // q becomes 2.92
var f = forwardMultiplyGate(q, z); // output is -11.59, up from -12! Nice!

Looks like that worked! Lets now try to interpret intuitively what just happened. The circuit wants to output higher values. The last gate saw inputs q = 3, z = -4 and computed output -12. “Pulling” upwards on this output value induced a force on both q and z: To increase the output value, the circuit “wants” z to increase, as can be seen by the positive value of the derivative(derivative_f_wrt_z = +3). Again, the size of this derivative can be interpreted as the magnitude of the force. On the other hand, q felt a stronger and downward force, since derivative_f_wrt_q = -4. In other words the circuit wants q to decrease, with a force of 4.

Now we get to the second, + gate which outputs q. By default, the + gate computes its derivatives which tells us how to change x and y to make q higher. BUT! Here is the crucial point: the gradient on q was computed as negative (derivative_f_wrt_q = -4), so the circuit wants q to decrease, and with a force of 4! So if the + gate wants to contribute to making the final output value larger, it needs to listen to the gradient signal coming from the top. In this particular case, it needs to apply tugs on x,y opposite of what it would normally apply, and with a force of 4, so to speak. The multiplication by -4 seen in the chain rule achieves exactly this: instead of applying a positive force of +1 on both x and y (the local derivative), the full circuit’s gradient on both x and y becomes 1 x -4 = -4. This makes sense: the circuit wants both x and y to get smaller because this will make q smaller, which in turn will make f larger.

If this makes sense, you understand backpropagation.

Lets recap once again what we learned:

• In the previous chapter we saw that in the case of a single gate (or a single expression), we can derive the analytic gradient using simple calculus. We interpreted the gradient as a force, or a tug on the inputs that pulls them in a direction which would make this gate’s output higher.

• In case of multiple gates everything stays pretty much the same way: every gate is hanging out by itself completely unaware of the circuit it is embedded in. Some inputs come in and the gate computes its output and the derivate with respect to the inputs. The only difference now is that suddenly, something can pull on this gate from above. That’s the gradient of the final circuit output value with respect to the ouput this gate computed. It is the circuit asking the gate to output higher or lower numbers, and with some force. The gate simply takes this force and multiplies it to all the forces it computed for its inputs before (chain rule). This has the desired effect:

1. If a gate experiences a strong positive pull from above, it will also pull harder on its own inputs, scaled by the force it is experiencing from above
2. And if it experiences a negative tug, this means that circuit wants its value to decrease not increase, so it will flip the force of the pull on its inputs to make its own output value smaller.

A nice picture to have in mind is that as we pull on the circuit’s output value at the end, this induces pulls downward through the entire circuit, all the way down to the inputs.

Isn’t it beautiful? The only difference between the case of a single gate and multiple interacting gates that compute arbitrarily complex expressions is this additional multipy operation that now happens in each gate.

Patterns in the “backward” flow

Lets look again at our example circuit with the numbers filled in. The first circuit shows the raw values, and the second circuit shows the gradients that flow back to the inputs as discussed. Notice that the gradient always starts off with +1 at the end to start off the chain. This is the (default) pull on the circuit to have its value increased.

 

 

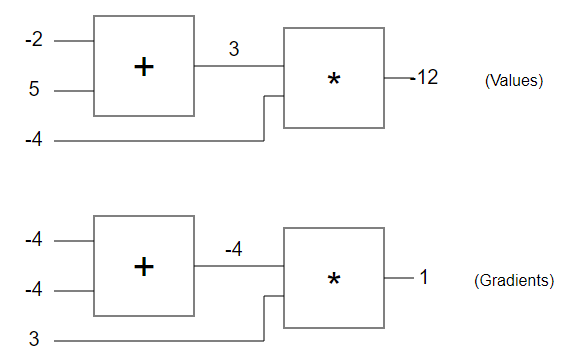
After a while you start to notice patterns in how the gradients flow backward in the circuits. For example, the + gate always takes the gradient on top and simply passes it on to all of its inputs (notice the example with -4 simply passed on to both of the inputs of + gate). This is because its own derivative for the inputs is just +1, regardless of what the actual values of the inputs are, so in the chain rule, the gradient from above is just multiplied by 1 and stays the same. Similar intuitions apply to, for example, a max(x,y) gate. Since the gradient of max(x,y) with respect to its input is +1 for whichever one of x, y is larger and 0 for the other, this gate is during backprop effectively just a gradient “switch”: it will take the gradient from above and “route” it to the input that had a higher value during the forward pass.

Numerical Gradient Check. Before we finish with this section, lets just make sure that the (analytic) gradient we computed by backprop above is correct as a sanity check. Remember that we can do this simply by computing the numerical gradient and making sure that we get [-4, -4, 3] for x,y,z. Here’s the code:

// initial conditions
var x = -2, y = 5, z = -4;

// numerical gradient check
var h = 0.0001;
var x_derivative = (forwardCircuit(x+h,y,z) - forwardCircuit(x,y,z)) / h; // -4
var y_derivative = (forwardCircuit(x,y+h,z) - forwardCircuit(x,y,z)) / h; // -4
var z_derivative = (forwardCircuit(x,y,z+h) - forwardCircuit(x,y,z)) / h; // 3

and we get [-4, -4, 3], as computed with backprop. phew! :)

 

next:  https://www.cnblogs.com/zhangzhiwei122/p/15887347.html