

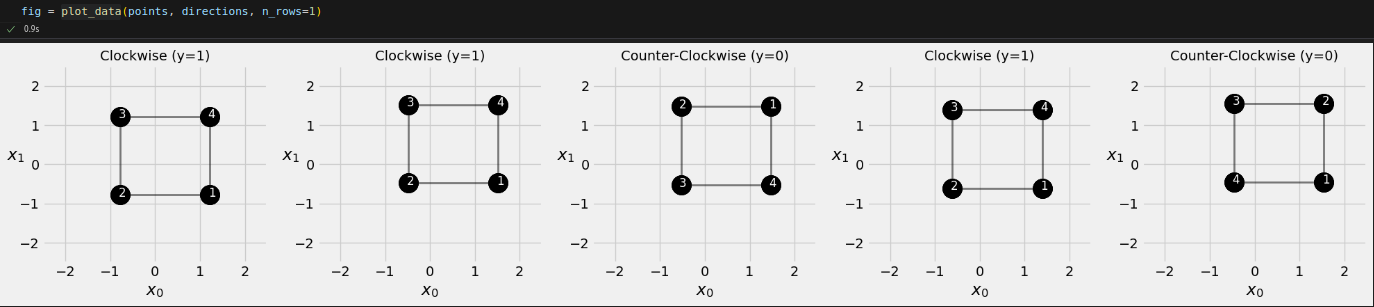
points, directions = generate_sequences(n=256, seed=13)
And then let’s visualize the first five squares:

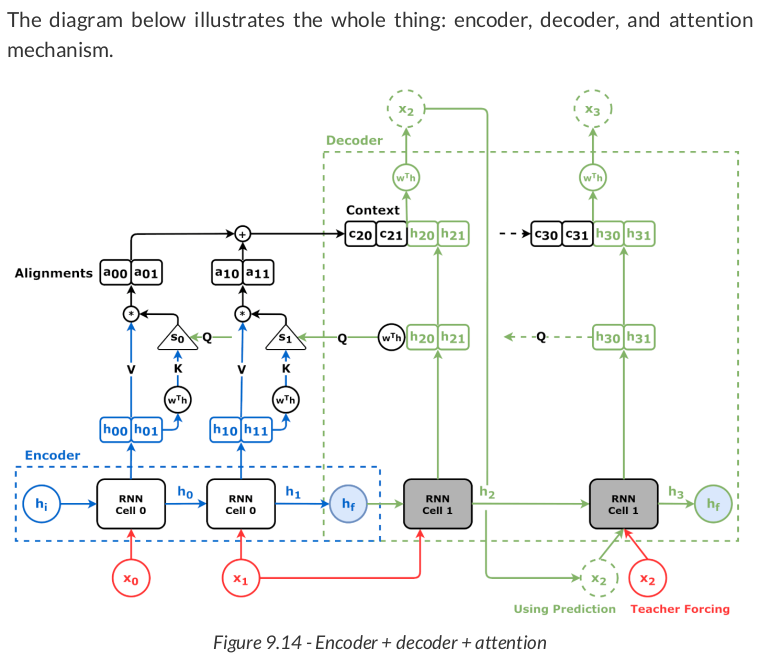
class Encoder(nn.Module): def __init__(self, n_features, hidden_dim): super().__init__() self.n_features = n_features self.hidden_dim = hidden_dim self.hidden = None self.basic_rnn = nn.GRU(self.n_features, self.hidden_dim, batch_first=True) def forward(self, x): rnn_out, self.hidden = self.basic_rnn(x) return rnn_out # N, L, F

coordinates of a "perfect" square and split it into source and target sequences:
full_seq = torch.tensor([[-1, -1], [-1, 1], [1, 1], [1, -1]]).float().view(1, 4, 2) source_seq = full_seq[:, :2] # first two corners target_seq = full_seq[:, 2:] # last two corners
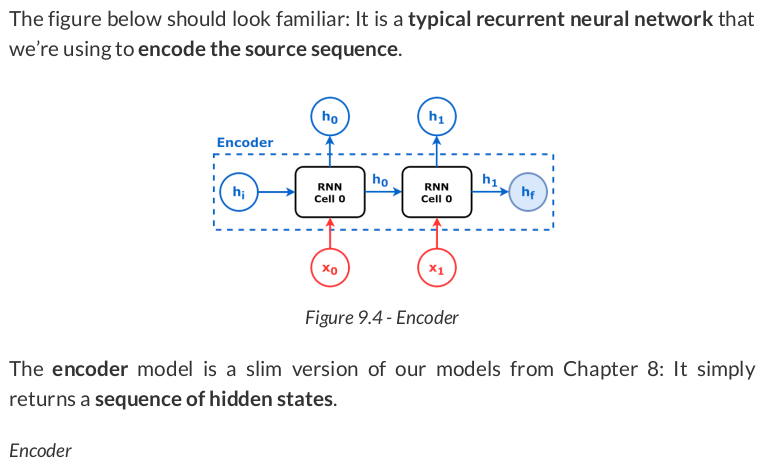
Now, let’s encode the source sequence and take the final hidden state:
torch.manual_seed(21) encoder = Encoder(n_features=2, hidden_dim=2) hidden_seq = encoder(source_seq) # output is N, L, F hidden_final = hidden_seq[:, -1:] # takes last hidden state hidden_final # tensor([[[ 0.3105, -0.5263]]], grad_fn=<SliceBackward0>)

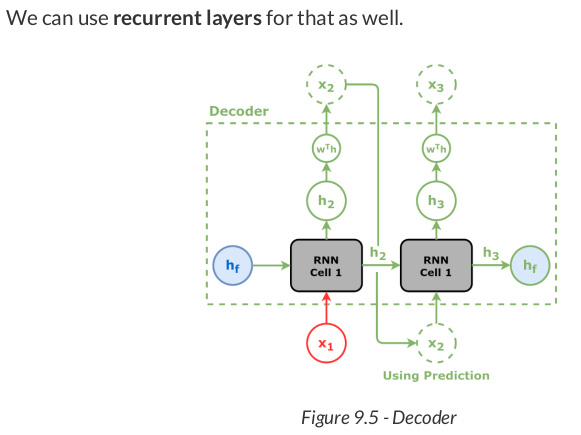



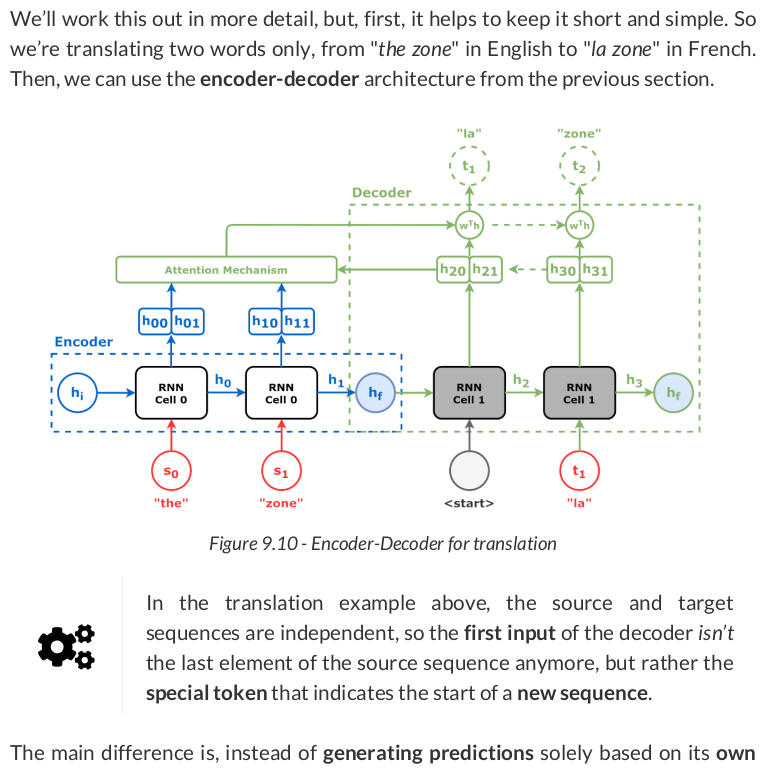
The decoder model is actually quite similar to the models we developed in Chapter 8:
class Decoder(nn.Module): def __init__(self, n_features, hidden_dim): super().__init__() self.n_features = n_features self.hidden_dim = hidden_dim self.hidden = None self.basic_rnn = nn.GRU(self.n_features, self.hidden_dim, batch_first=True) self.regression = nn.Linear(self.hidden_dim, self.n_features) def init_hidden(self, hidden_seq): # We only need the final hidden state hidden_final = hidden_seq[:, -1:] # N, 1, H # Initialize decoder’s hidden state using encoder’s final hidden state. # But we need to make it sequence-first self.hidden = hidden_final.permute(1, 0, 2) # 1, N, H def forward(self, x): # x is N, 1, F # The recurrent layer both uses and updates the hidden state. batch_first_output, self.hidden = self.basic_rnn(x, self.hidden) last_output = batch_first_output[:, -1:] out = self.regression(last_output) # The output has the same shape as the input (N, 1, F). return out.view(-1, 1, self.n_features)


torch.manual_seed(21) decoder = Decoder(n_features=2, hidden_dim=2) # Initial hidden state will be encoder's final hidden state decoder.init_hidden(hidden_seq) # Initial data point is the last element of source sequence inputs = source_seq[:, -1:] target_len = 2 for i in range(target_len): print(f'Hidden: {decoder.hidden}') out = decoder(inputs) # Predicts coordinates print(f'Output: {out}\n') # Predicted coordinates are next step's inputs inputs = out
Hidden: tensor([[[ 0.3105, -0.5263]]], grad_fn=<PermuteBackward0>) Output: tensor([[[-0.2339, 0.4702]]], grad_fn=<ViewBackward0>) Hidden: tensor([[[ 0.3913, -0.6853]]], grad_fn=<StackBackward0>) Output: tensor([[[-0.0226, 0.4628]]], grad_fn=<ViewBackward0>)


# Initial hidden state will be encoder's final hidden state decoder.init_hidden(hidden_seq) # Initial data point is the last element of source sequence inputs = source_seq[:, -1:] target_len = 2 for i in range(target_len): print(f'Hidden: {decoder.hidden}') out = decoder(inputs) # Predicts coordinates print(f'Output: {out}\n') # But completely ignores the predictions and uses real data instead inputs = target_seq[:, i:i+1]
Hidden: tensor([[[ 0.3105, -0.5263]]], grad_fn=<PermuteBackward0>) Output: tensor([[[-0.2339, 0.4702]]], grad_fn=<ViewBackward0>) Hidden: tensor([[[ 0.3913, -0.6853]]], grad_fn=<StackBackward0>) Output: tensor([[[0.2265, 0.4529]]], grad_fn=<ViewBackward0>)
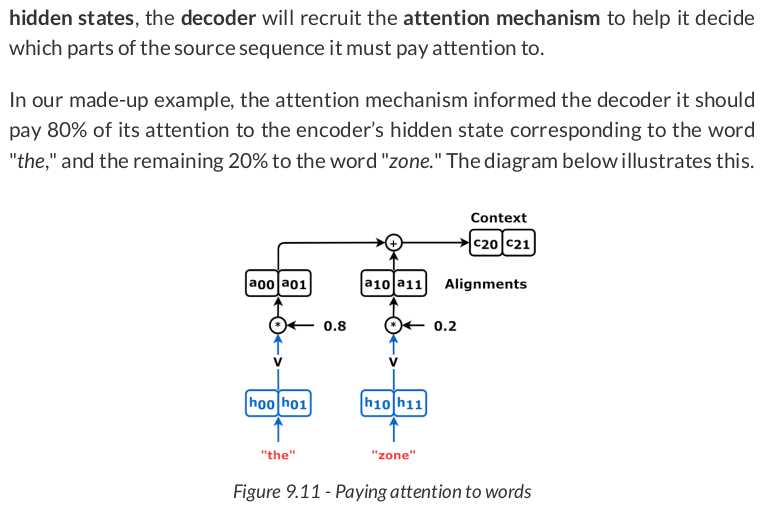
Now, a bad prediction can only be traced to the model itself, and any bad predictions in previous steps have no effect whatsoever.

# Initial hidden state is encoder's final hidden state decoder.init_hidden(hidden_seq) # Initial data point is the last element of source sequence inputs = source_seq[:, -1:] teacher_forcing_prob = 0.5 target_len = 2 for i in range(target_len): print(f'Hidden: {decoder.hidden}') out = decoder(inputs) print(f'Output: {out}\n') # If it is teacher forcing if torch.rand(1) <= teacher_forcing_prob: # Takes the actual element inputs = target_seq[:, i:i+1] else: # Otherwise uses the last predicted output inputs = out
Hidden: tensor([[[ 0.3105, -0.5263]]], grad_fn=<PermuteBackward0>) Output: tensor([[[-0.2339, 0.4702]]], grad_fn=<ViewBackward0>) Hidden: tensor([[[ 0.3913, -0.6853]]], grad_fn=<StackBackward0>) Output: tensor([[[-0.0226, 0.4628]]], grad_fn=<ViewBackward0>)
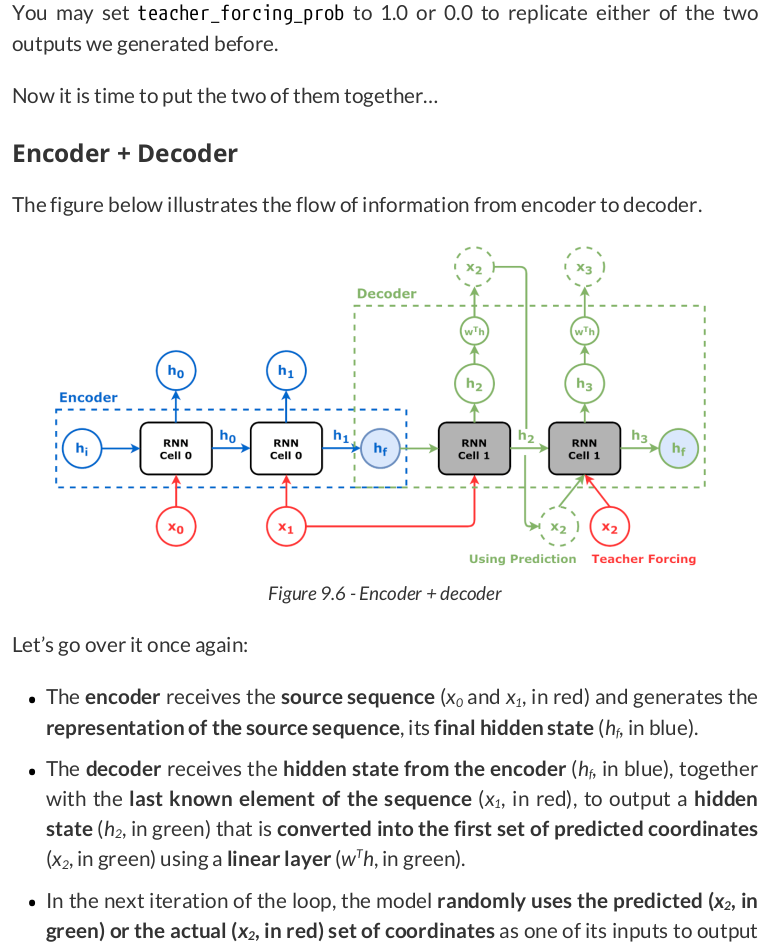

class EncoderDecoder(nn.Module): def __init__(self, encoder, decoder, input_len, target_len, teacher_forcing_prob=0.5): super().__init__() self.encoder = encoder self.decoder = decoder self.input_len = input_len self.target_len = target_len self.teacher_forcing_prob = teacher_forcing_prob self.outputs = None def init_outputs(self, batch_size): device = next(self.parameters()).device # N, L (target), F self.outputs = torch.zeros(batch_size, self.target_len, self.encoder.n_features).to(device) def store_output(self, i, out): # Stores the output self.outputs[:, i:i+1, :] = out def forward(self, x): # splits the data in source and target sequences # the target seq will be empty in testing mode # N, L, F source_seq = x[:, :self.input_len, :] target_seq = x[:, self.input_len:, :] self.init_outputs(x.shape[0]) # Encoder expected N, L, F hidden_seq = self.encoder(source_seq) # Output is N, L, H self.decoder.init_hidden(hidden_seq) # The last input of the encoder is also # the first input of the decoder dec_inputs = source_seq[:, -1:, :] # Generates as many outputs as the target length for i in range(self.target_len): # Output of decoder is N, 1, F out = self.decoder(dec_inputs) self.store_output(i, out) prob = self.teacher_forcing_prob # In evaluation/test the target sequence is # unknown, so we cannot use teacher forcing if not self.training: prob = 0 # If it is teacher forcing if torch.rand(1) <= prob: # Takes the actual element dec_inputs = target_seq[:, i:i+1, :] else: # Otherwise uses the last predicted output dec_inputs = out return self.outputs

Let’s create an instance of the model above using the other two we already created:
encdec = EncoderDecoder(encoder, decoder, input_len=2, target_len=2, teacher_forcing_prob=0.5)
In training mode, the model expects the full sequence so it can randomly use teacher forcing:
encdec.train()
encdec(full_seq)
tensor([[[-0.2339, 0.4702],
[ 0.2265, 0.4529]]], grad_fn=<CopySlices>)
In evaluation / test mode, though, it only needs the source sequence as input:
encdec.eval()
encdec(source_seq)
tensor([[[-0.2339, 0.4702],
[-0.0226, 0.4628]]], grad_fn=<CopySlices>)

Data Generation — Train
points, directions = generate_sequences(n=256, seed=13) full_train = torch.as_tensor(np.array(points)).float() target_train = full_train[:, 2:]
For the test set, though, we only need the source sequences as features (X) and the target sequences as labels (y):
Data Generation — Test
test_points, test_directions = generate_sequences(seed=19) full_test = torch.as_tensor(test_points).float() source_test = full_test[:, :2] target_test = full_test[:, 2:]
These are all simple tensors, so we can use TensorDatasets and simple data loaders:
Data Preparation
train_data = TensorDataset(full_train, target_train) test_data = TensorDataset(source_test, target_test) generator = torch.Generator() train_loader = DataLoader(train_data, batch_size=16, shuffle=True, generator=generator) test_loader = DataLoader(test_data, batch_size=16)


torch.manual_seed(23) encoder = Encoder(n_features=2, hidden_dim=2) decoder = Decoder(n_features=2, hidden_dim=2) model = EncoderDecoder(encoder, decoder, input_len=2, target_len=2, teacher_forcing_prob=0.5) loss_fn = nn.MSELoss() optimizer = optim.Adam(model.parameters(), lr=0.01)
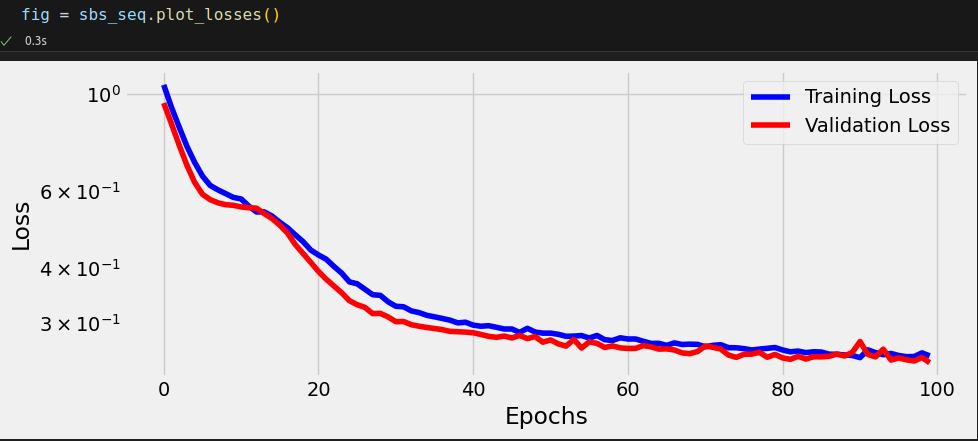
Next, we use the StepByStep class to train the model:
Model Training
sbs_seq = StepByStep(model, loss_fn, optimizer)
sbs_seq.set_loaders(train_loader, test_loader)
sbs_seq.train(100)

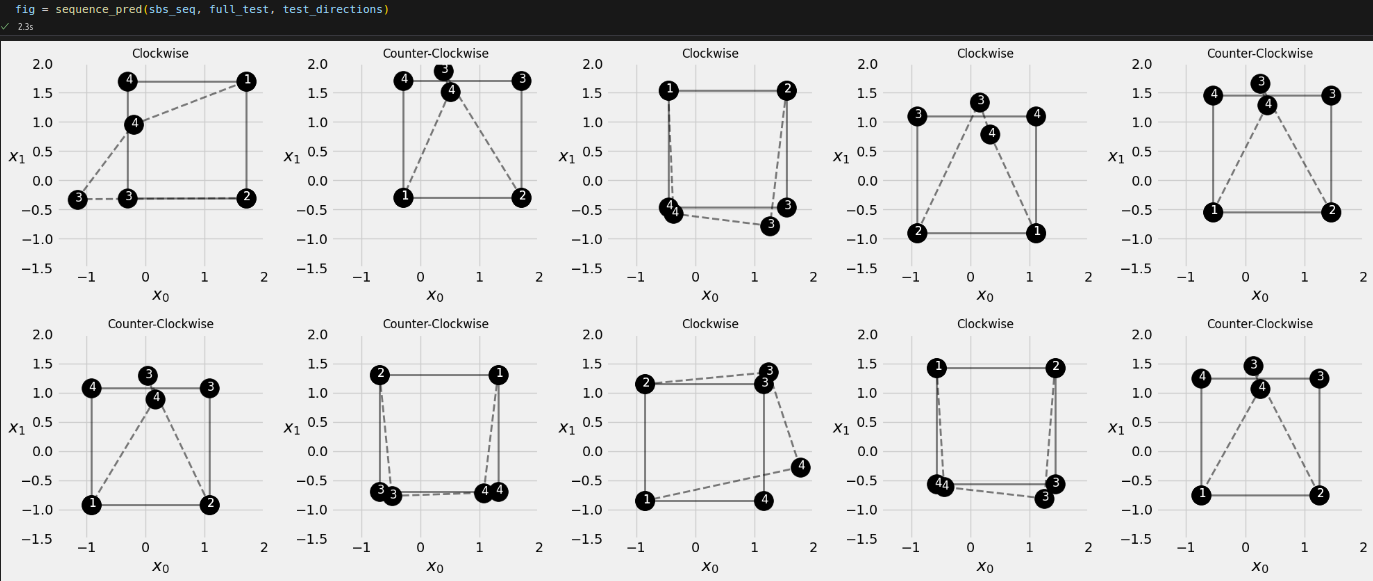









full_seq = torch.tensor([[-1, -1], [-1, 1], [1, 1], [1, -1]]).float().view(1, 4, 2) source_seq = full_seq[:, :2] target_seq = full_seq[:, 2:]
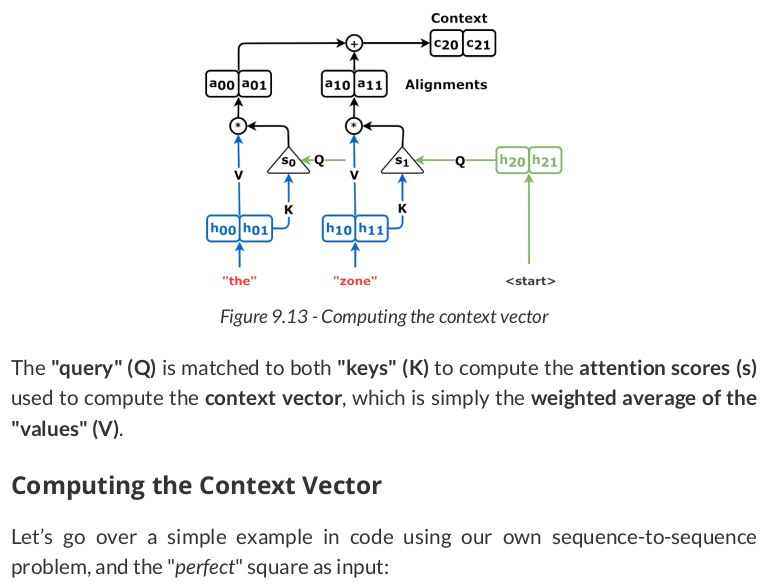
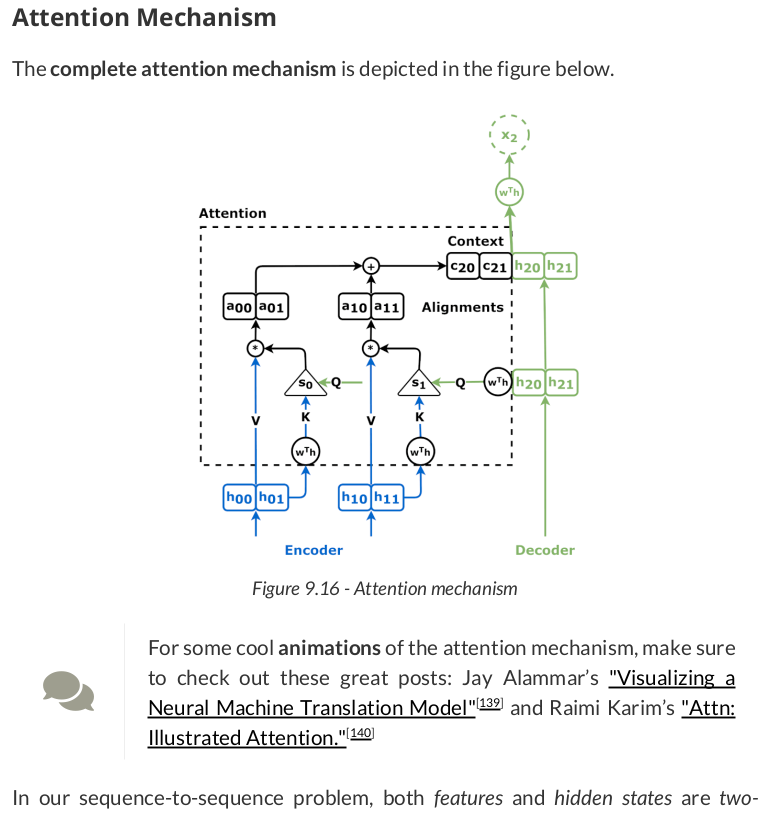
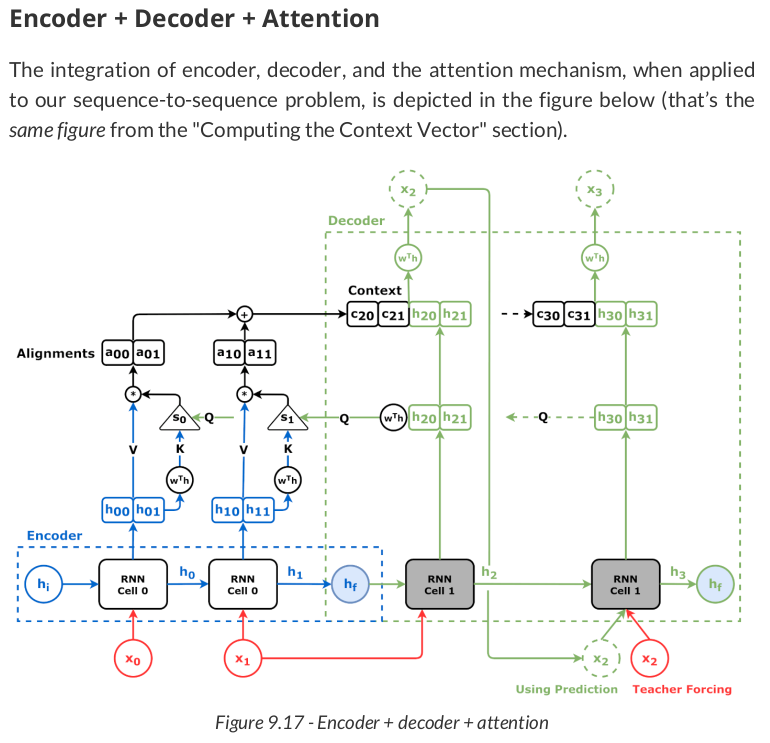
The source sequence is the input of the encoder, and the hidden states it outputs are going to be both "values" (V) and "keys" (K):
torch.manual_seed(21) encoder = Encoder(n_features=2, hidden_dim=2) hidden_seq = encoder(source_seq) values = hidden_seq # N, L, H values
tensor([[[ 0.0832, -0.0356],
[ 0.3105, -0.5263]]], grad_fn=<TransposeBackward1>)
keys = hidden_seq # N, L, H keys
tensor([[[ 0.0832, -0.0356],
[ 0.3105, -0.5263]]], grad_fn=<TransposeBackward1>)

torch.manual_seed(21) decoder = Decoder(n_features=2, hidden_dim=2) decoder.init_hidden(hidden_seq) inputs = source_seq[:, -1:] out = decoder(inputs)
The first "query" (Q) is the decoder’s hidden state (remember, hidden states are always sequence-first, so we’re permuting it to batch-first):
query = decoder.hidden.permute(1, 0, 2) # N, 1, H query # tensor([[[ 0.3913, -0.6853]]], grad_fn=<PermuteBackward0>)
OK, we have the "keys" and a "query," so let’s pretend we can compute attention scores (alphas) using them:
def calc_alphas(ks, q): N, L, H = ks.size() alphas = torch.ones(N, 1, L).float() * 1/L return alphas alphas = calc_alphas(keys, query) alphas # tensor([[[0.5000, 0.5000]]])

# N, 1, L x N, L, H -> 1, L x L, H -> 1, H context_vector = torch.bmm(alphas, values) context_vector # tensor([[[ 0.1968, -0.2809]]], grad_fn=<BmmBackward0>)


concatenated = torch.cat([context_vector, query], axis=-1) concatenated # tensor([[[ 0.1968, -0.2809, 0.3913, -0.6853]]], grad_fn=<CatBackward0>)





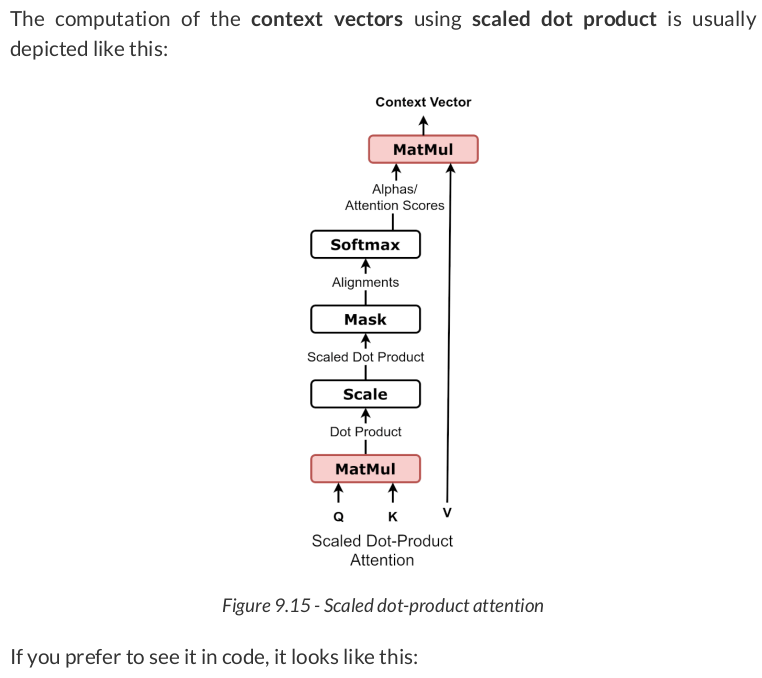
# N, 1, H x N, H, L -> N, 1, L products = torch.bmm(query, keys.permute(0, 2, 1)) products # tensor([[[0.0569, 0.4821]]], grad_fn=<BmmBackward0>)

alphas = F.softmax(products, dim=-1) alphas # tensor([[[0.3953, 0.6047]]], grad_fn=<SoftmaxBackward0>)


def calc_alphas(ks, q): # N, 1, H x N, H, L -> N, 1, L products = torch.bmm(q, ks.permute(0, 2, 1)) alphas = F.softmax(products, dim=-1) return alphas

q = torch.tensor([.55, .95]).view(1, 1, 2) # N, 1, H k = torch.tensor([[.65, .2], [.85, -.4], [-.95, -.75]]).view(1, 3, 2) # N, L, H
Then, let’s visualize them as vectors, together with their norms and the cosines of the angles between each "key" and the "query."

We can use the values in the figure above to compute the dot product between each "key" and the "query":

Equation 9.7 - Dot products
# N, 1, H x N, H, L -> N, 1, L prod = torch.bmm(q, k.permute(0, 2, 1)) prod # tensor([[[ 0.5475, 0.0875, -1.2350]]])

scores = F.softmax(prod, dim=-1) scores # tensor([[[0.5557, 0.3508, 0.0935]]])

v = k context = torch.bmm(scores, v) context # tensor([[[ 0.5706, -0.0993]]])
Better yet, let’s visualize the context vector.



dims = query.size(-1) scaled_products = products / np.sqrt(dims) scaled_products # tensor([[[0.0403, 0.3409]]], grad_fn=<DivBackward0>)

n_dims = 10
vector1 = torch.randn(10000, 1, n_dims)
vector2 = torch.randn(10000, 1, n_dims).permute(0, 2, 1)
torch.bmm(vector1, vector2).squeeze().var()
# tensor(9.7670)


dummy_product = torch.tensor([4.0, 1.0]) F.softmax(dummy_product, dim=-1), F.softmax(100*dummy_product, dim=-1) # (tensor([0.9526, 0.0474]), tensor([1., 0.]))

alphas = F.softmax(scaled_products, dim=-1) alphas # tensor([[[0.4254, 0.5746]]], grad_fn=<SoftmaxBackward0>)
def calc_alphas(ks, q): dims = q.size(-1) # N, 1, H x N, H, L -> N, 1, L products = torch.bmm(q, ks.permute(0, 2, 1)) scaled_products = products / np.sqrt(dims) alphas = F.softmax(scaled_products, dim=-1) return alphas
alphas = calc_alphas(keys, query) # N, 1, L x N, L, H -> 1, L x L, H -> 1, H context_vector = torch.bmm(alphas, values) context_vector # tensor([[[ 0.2138, -0.3175]]], grad_fn=<BmmBackward0>)


class Attention(nn.Module): def __init__(self, hidden_dim, input_dim=None, proj_values=False): super().__init__() self.d_k = hidden_dim self.input_dim = hidden_dim if input_dim is None else input_dim self.proj_values = proj_values # Affine transformations for Q, K, and V self.linear_query = nn.Linear(self.input_dim, hidden_dim) self.linear_key = nn.Linear(self.input_dim, hidden_dim) self.linear_value = nn.Linear(self.input_dim, hidden_dim) self.alphas = None def init_keys(self, keys): self.keys = keys self.proj_keys = self.linear_key(self.keys) self.values = self.linear_value(self.keys) if self.proj_values else self.keys def score_function(self, query): proj_query = self.linear_query(query) # scaled dot product # N, 1, H x N, H, L -> N, 1, L dot_products = torch.bmm(proj_query, self.proj_keys.permute(0, 2, 1)) scores = dot_products / np.sqrt(self.d_k) return scores def forward(self, query, mask=None): # First step: Alignment scores (scaled dot product) # Query is batch-first N, 1, H scores = self.score_function(query) # N, 1, L if mask is not None: scores = scores.masked_fill(mask == 0, -1e9) # Second step: Attention scores (alphas) alphas = F.softmax(scores, dim=-1) # N, 1, L self.alphas = alphas.detach() # Third step: Context vector # N, 1, L x N, L, H -> N, 1, H context = torch.bmm(alphas, self.values) return context



source_seq = torch.tensor([[[-1., 1.], [0., 0.]]]) # pretend there's an encoder here... keys = torch.tensor([[[-.38, .44], [.85, -.05]]]) query = torch.tensor([[[-1., 1.]]])

source_mask = (source_seq != 0).all(axis=2).unsqueeze(1) source_mask # N, 1, L # tensor([[[ True, False]]])

torch.manual_seed(11) attnh = Attention(2) attnh.init_keys(keys) context = attnh(query, mask=source_mask) attnh.alphas # tensor([[[1., 0.]]])

class DecoderAttn(nn.Module): def __init__(self, n_features, hidden_dim): super().__init__() self.hidden_dim = hidden_dim self.n_features = n_features self.hidden = None self.basic_rnn = nn.GRU(self.n_features, self.hidden_dim, batch_first=True) self.attn = Attention(self.hidden_dim) self.regression = nn.Linear(2 * self.hidden_dim, self.n_features) def init_hidden(self, hidden_seq): # the output of the encoder is N, L, H # and init_keys expects batch-first as well self.attn.init_keys(hidden_seq) hidden_final = hidden_seq[:, -1:] self.hidden = hidden_final.permute(1, 0, 2) # L, N, H def forward(self, X, mask=None): # X is N, 1, F batch_first_output, self.hidden = self.basic_rnn(X, self.hidden) query = batch_first_output[:, -1:] # Attention context = self.attn(query, mask=mask) concatenated = torch.cat([context, query], axis=-1) out = self.regression(concatenated) # N, 1, F return out.view(-1, 1, self.n_features)
Let’s go over a simple example in code, using the updated decoder and attention classes:
full_seq = torch.tensor([[-1, -1], [-1, 1], [1, 1], [1, -1]]).float().view(1, 4, 2) source_seq = full_seq[:, :2] target_seq = full_seq[:, 2:]
torch.manual_seed(21) encoder = Encoder(n_features=2, hidden_dim=2) decoder_attn = DecoderAttn(n_features=2, hidden_dim=2) # Generates hidden states (keys and values) hidden_seq = encoder(source_seq) decoder_attn.init_hidden(hidden_seq) # Target sequence generation inputs = source_seq[:, -1:] target_len = 2 for i in range(target_len): out = decoder_attn(inputs) print(f'Output: {out}') inputs = out
Output: tensor([[[-0.3555, -0.1220]]], grad_fn=<ViewBackward0>)
Output: tensor([[[-0.2641, -0.2521]]], grad_fn=<ViewBackward0>)


encdec = EncoderDecoder(encoder, decoder_attn, input_len=2, target_len=2, teacher_forcing_prob=0.0)
encdec(full_seq)
tensor([[[-0.3555, -0.1220],
[-0.2641, -0.2521]]], grad_fn=<CopySlices>)

class EncoderDecoderAttn(EncoderDecoder): def __init__(self, encoder, decoder, input_len, target_len, teacher_forcing_prob=0.5): super().__init__(encoder, decoder, input_len, target_len, teacher_forcing_prob) self.alphas = None def init_outputs(self, batch_size): device = next(self.parameters()).device # N, L (target), F self.outputs = torch.zeros(batch_size, self.target_len, self.encoder.n_features).to(device) # N, L (target), L (source) self.alphas = torch.zeros(batch_size, self.target_len, self.input_len).to(device) def store_output(self, i, out): # Stores the output self.outputs[:, i:i+1, :] = out self.alphas[:, i:i+1, :] = self.decoder.attn.alphas

torch.manual_seed(23) encoder = Encoder(n_features=2, hidden_dim=2) decoder_attn = DecoderAttn(n_features=2, hidden_dim=2) model = EncoderDecoderAttn(encoder, decoder_attn, input_len=2, target_len=2, teacher_forcing_prob=0.5) loss_fn = nn.MSELoss() optimizer = optim.Adam(model.parameters(), lr=0.01)
Model Training
sbs_seq_attn = StepByStep(model, loss_fn, optimizer)
sbs_seq_attn.set_loaders(train_loader, test_loader)
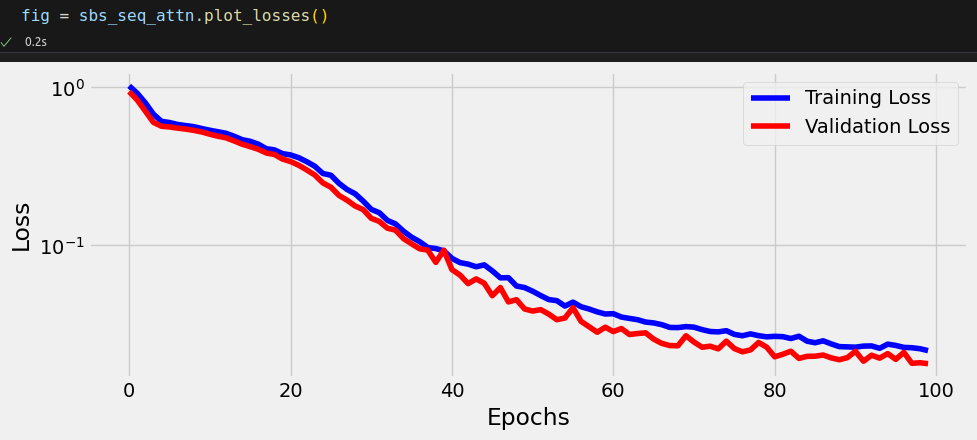
sbs_seq_attn.train(100)

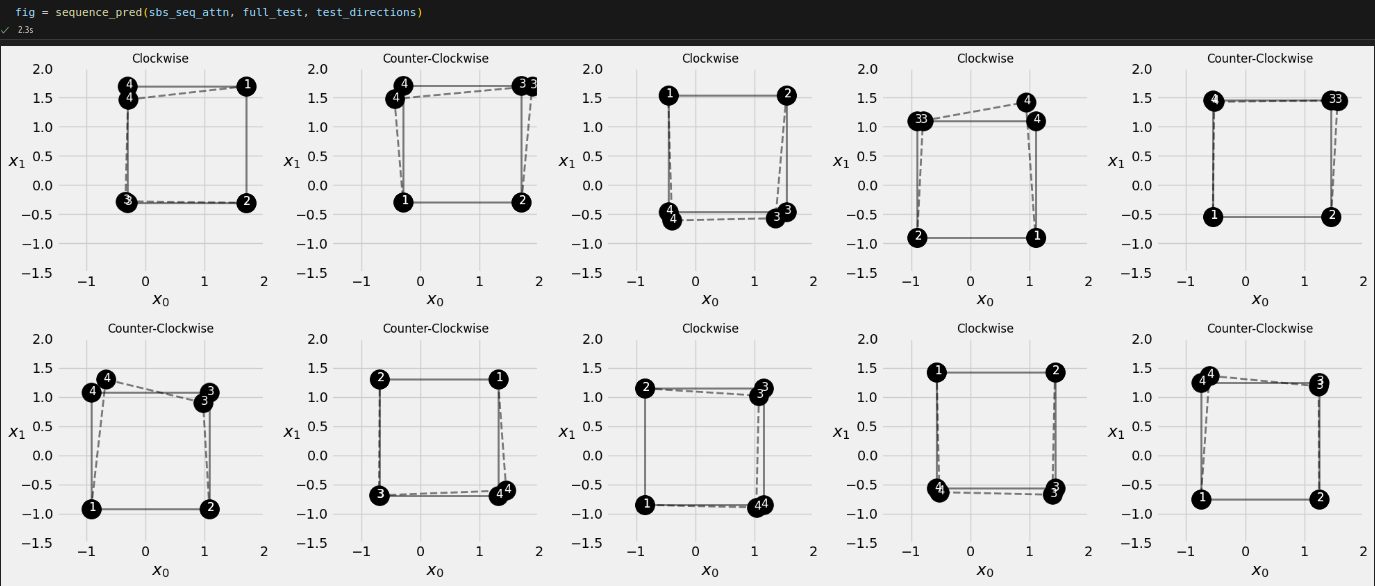


inputs = full_train[:1, :2] out = sbs_seq_attn.predict(inputs) sbs_seq_attn.model.alphas
tensor([[[9.9052e-01, 9.4753e-03], [1.2264e-04, 9.9988e-01]]], device='cuda:0')

inputs = full_train[:10, :2] source_labels = ['Point #1', 'Point #2'] target_labels = ['Point #3', 'Point #4'] point_labels = [f'{"Counter-" if not directions[i] else ""}Clockwise\nPoint #1: {inp[0, 0]:.2f}, {inp[0, 1]:.2f}' for i, inp in enumerate(inputs)]


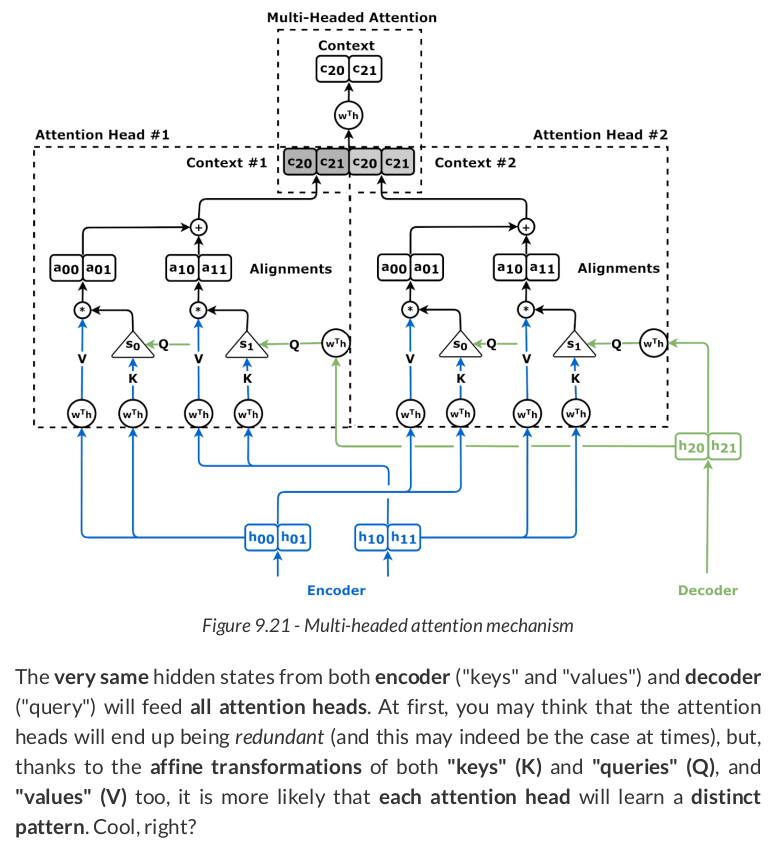


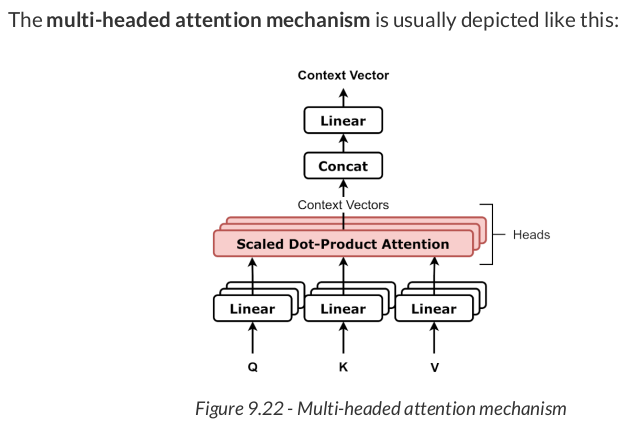
The code for the multi-headed attention mechanism looks like this:
class MultiHeadAttention(nn.Module): def __init__(self, n_heads, d_model, input_dim=None, proj_values=True): super().__init__() self.linear_out = nn.Linear(n_heads * d_model, d_model) self.attn_heads = nn.ModuleList([Attention(d_model, input_dim=input_dim, proj_values=proj_values) for _ in range(n_heads)]) def init_keys(self, key): for attn in self.attn_heads: attn.init_keys(key) @property def alphas(self): # Shape: n_heads, N, 1, L (source) return torch.stack([attn.alphas for attn in self.attn_heads], dim=0) def output_function(self, contexts): # N, 1, n_heads * D concatenated = torch.cat(contexts, axis=-1) # Linear transf. to go back to original dimension out = self.linear_out(concatenated) # N, 1, D return out def forward(self, query, mask=None): contexts = [attn(query, mask=mask) for attn in self.attn_heads] out = self.output_function(contexts) return out





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律