


https://storage.googleapis.com/download.tensorflow.org/data/rps.zip
https://storage.googleapis.com/download.tensorflow.org/data/rps-test-set.zip




temp_transform = Compose([Resize(28), ToImage(), ToDtype(torch.float32, scale=True)]) temp_dataset = ImageFolder(root='rps', transform=temp_transform)

temp_dataset[0][0].shape, temp_dataset[0][1] # (torch.Size([3, 28, 28]), 0)

temp_loader = DataLoader(temp_dataset, batch_size=16)

@staticmethod def statistics_per_channel(images, labels): # NCHW n_samples, n_channels, n_height, n_weight = images.size() # Flatten HW to a single dimension flatten_per_channel = images.reshape(n_samples, n_channels, -1) # Compute statistics of each image per channel # Average pixel value per channel # (n_samples, n_channels) means = flatten_per_channel.mean(axis=2) # Standard deviation of pixel values per channel # (n_samples, n_channels) stds = flatten_per_channel.std(axis=2) # Add up statistics of all images in a mini-batch # (1, n_channels) sum_means = means.sum(axis=0) sum_stds = stds.sum(axis=0) # Make a tensor of shape (1, n_channels) with the number of samples in the mini-batch # [16] * 3 = [16, 16, 16] n_samples = torch.tensor([n_samples] * n_channels).float() # Stack the three tensors on top of one another # (3, n_channels) return torch.stack([n_samples, sum_means, sum_stds], axis=0)
first_images, first_labels = next(iter(temp_loader))
StepByStep.statistics_per_channel(first_images, first_labels)
tensor([[16.0000, 16.0000, 16.0000], [13.8748, 13.3048, 13.1962], [ 3.0507, 3.8268, 3.9754]])

results = StepByStep.loader_apply(temp_loader, StepByStep.statistics_per_channel)
results
tensor([[2520.0000, 2520.0000, 2520.0000], [2142.5356, 2070.0806, 2045.1444], [ 526.3025, 633.0677, 669.9556]])

@staticmethod def make_normalizer(loader): total_samples, total_means, total_stds = StepByStep.loader_apply(loader, StepByStep.statistics_per_channel) norm_mean = total_means / total_samples norm_std = total_stds / total_samples return Normalize(mean=norm_mean, std=norm_std)

normalizer = StepByStep.make_normalizer(temp_loader) normalizer # Normalize(mean=[tensor(0.8502), tensor(0.8215), tensor(0.8116)], std=[tensor(0.2089), tensor(0.2512), tensor(0.2659)], inplace=False)


composer = Compose([Resize(28), ToImage(), ToDtype(torch.float32, scale=True), normalizer]) train_data = ImageFolder(root='rps', transform=composer) val_data = ImageFolder(root='rps-test-set', transform=composer) train_loader = DataLoader(train_data, batch_size=16, shuffle=True) val_loader = DataLoader(val_data, batch_size=16)


Figure 6.2 - Training set (normalized)


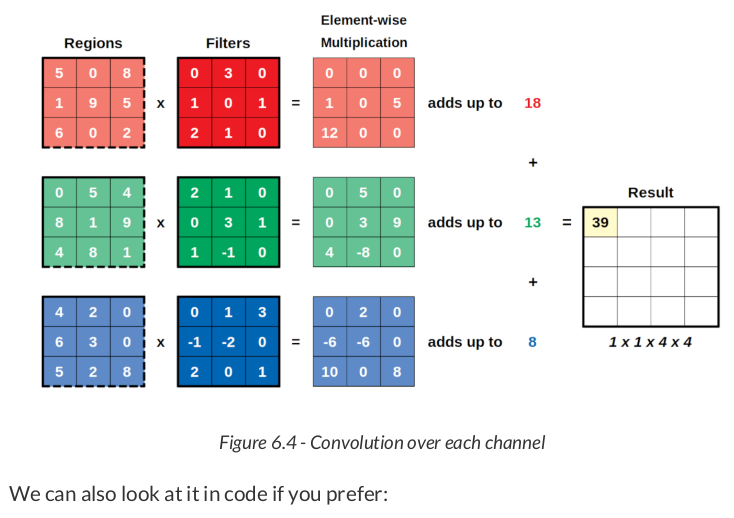
regions = np.array([[[[5, 0, 8], [1, 9, 5], [6, 0, 2]], [[0, 5, 4], [8, 1, 9], [4, 8, 1]], [[4, 2, 0], [6, 3, 0], [5, 2, 8]]]]) regions.shape # (1, 3, 3, 3) three_channel_filter = np.array([[[[0, 3, 0], [1, 0, 1], [2, 1, 0]], [[2, 1, 0], [0, 3, 1], [1, -1, 0]], [[0, 1, 3], [-1, -2, 0], [2, 0, 1]]]]) three_channel_filter.shape # (1, 3, 3, 3) result = F.conv2d(torch.as_tensor(regions), torch.as_tensor(three_channel_filter)) result, result.shape # (tensor([[[[39]]]]), torch.Size([1, 1, 1, 1]))


class CNN2(nn.Module): def __init__(self, n_feature, p=.0): super(CNN2, self).__init__() self.n_feature = n_feature self.p = p # Create the convolution layers self.conv1 = nn.Conv2d(in_channels=3, out_channels=n_feature, kernel_size=3) self.conv2 = nn.Conv2d(in_channels=n_feature, out_channels=n_feature, kernel_size=3) # Create the linear (fully-connected) layers # Where do this 5 * 5 come from?! Check it below self.fc1 = nn.Linear(n_feature * 5 * 5, 50) self.fc2 = nn.Linear(50, 3) # Create dropout layers self.drop = nn.Dropout(self.p)

Let’s create our two convolutional blocks in a method aptly named featurizer:
def featurizer(self, x): # Featurizer # First convolutional block # 3@28x28 -> n_feature@26x26 -> n_feature@13x13 x = self.conv1(x) x = F.relu(x) x = F.max_pool2d(x, kernel_size=2) # Second convolutional block # n_feature@13x13 -> n_feature@11x11 -> n_feature@5x5 x = self.conv2(x) x = F.relu(x) x = F.max_pool2d(x, kernel_size=2) # Input dimension (n_feature@5x5) # Output dimension (n_feature * 5 * 5) x = nn.Flatten()(x) return x

def classifier(self, x): # Classifier # Hidden Layer # Input dimension (n_feature * 5 * 5) # Output dimension (50) if self.p > 0: x = self.drop(x) x = self.fc1(x) x = F.relu(x) # Output Layer # Input dimension (50) # Output dimension (3) if self.p > 0: x = self.drop(x) x = self.fc2(x) return x

def forward(self, x): x = self.featurizer(x) x = self.classifier(x) return x


dropping_model = nn.Sequential(nn.Dropout(p=0.5))

spaced_points = torch.linspace(.1, 1.1, 11) spaced_points # tensor([0.1000, 0.2000, 0.3000, 0.4000, 0.5000, 0.6000, 0.7000, 0.8000, 0.9000, 1.0000, 1.1000])
Next, let’s use these points as inputs of our amazingly simple model:
torch.manual_seed(44) dropping_model.train() output_train = dropping_model(spaced_points) output_train # tensor([0.0000, 0.4000, 0.0000, 0.8000, 0.0000, 1.2000, 1.4000, 1.6000, 1.8000, 0.0000, 2.2000])
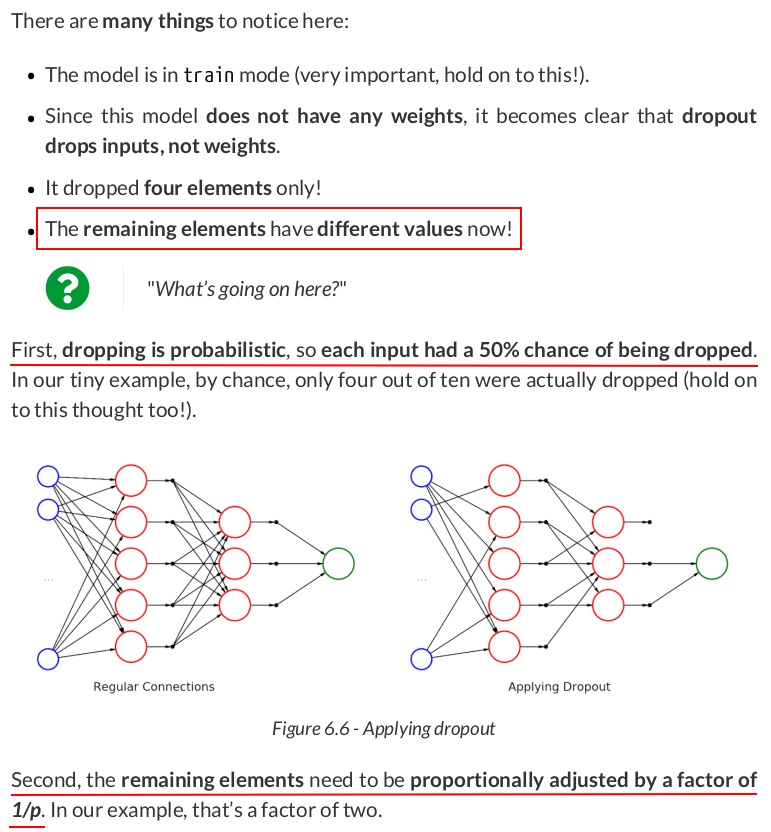
output_train / spaced_points # tensor([0., 2., 0., 2., 0., 2., 2., 2., 2., 0., 2.])

F.linear(output_train, weight=torch.ones(11), bias=torch.tensor(0)) # tensor(9.4000)

dropping_model.eval() output_eval = dropping_model(spaced_points) output_eval # tensor([0.1000, 0.2000, 0.3000, 0.4000, 0.5000, 0.6000, 0.7000, 0.8000, 0.9000, 1.0000, 1.1000])

F.linear(output_eval, weight=torch.ones(11), bias=torch.tensor(0)) # tensor(6.6000)

torch.manual_seed(17) p = 0.5 distrib_outputs = torch.tensor([F.linear(F.dropout(spaced_points, p=0.5), weight=torch.ones(11), bias=torch.tensor(0)) for _ in range(1000)])









lr = 3e-4 torch.manual_seed(13) model_cnn2 = CNN2(n_feature=5, p=.3) ce_loss_fn = nn.CrossEntropyLoss(reduction='mean') optimizer_cnn2 = optim.Adam(model_cnn2.parameters(), lr=lr)
sbs_cnn2 = StepByStep(model_cnn2, ce_loss_fn, optimizer_cnn2)
sbs_cnn2.set_loaders(train_loader, val_loader)
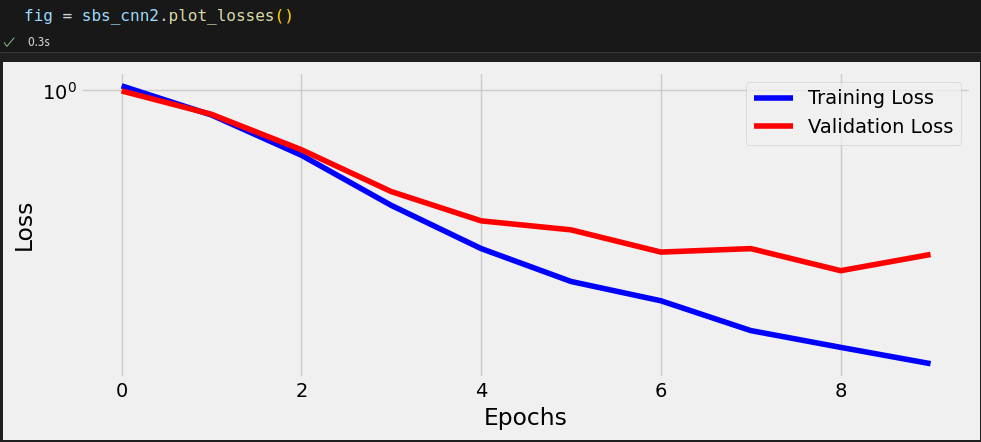
sbs_cnn2.train(10)
1m25s
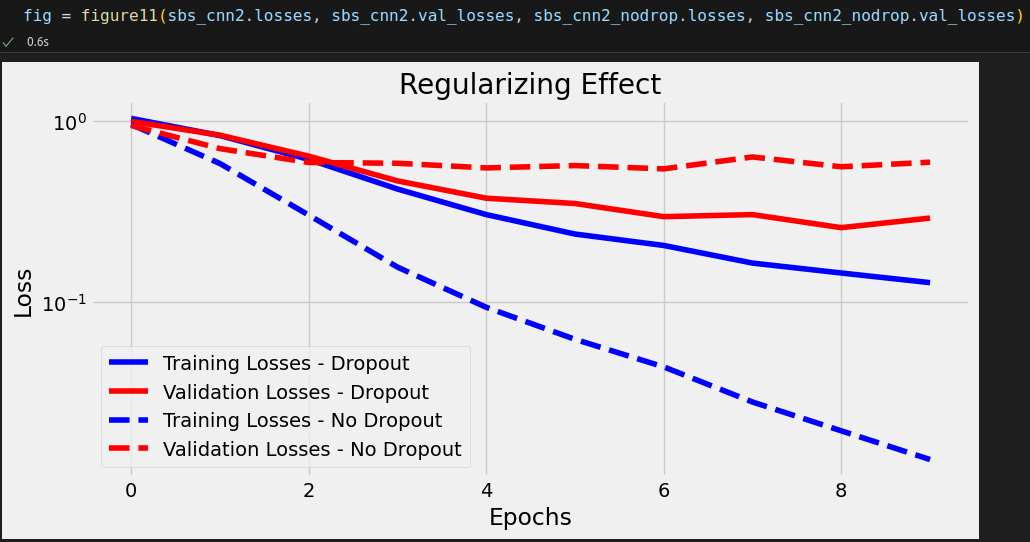
You should expect training to take a while since this model is more complex than previous ones (6,823 parameters against 213 parameters for the last chapter’s model). After it finishes, the computed losses should look like this:

StepByStep.loader_apply(val_loader, sbs_cnn2.correct)
tensor([[ 93, 124], [119, 124], [115, 124]])
The model got 327 out of 372 right. That’s 87.9% accuracy on the validation set—not bad!

lr = 3e-4 torch.manual_seed(13) # Model configuration model_cnn2_nodrop = CNN2(n_feature=5, p=.0) ce_loss_fn = nn.CrossEntropyLoss(reduction='mean') optimizer_cnn2_nodrop = optim.Adam(model_cnn2_nodrop.parameters(), lr=lr) # Model training sbs_cnn2_nodrop = StepByStep(model_cnn2_nodrop, ce_loss_fn, optimizer_cnn2_nodrop) sbs_cnn2_nodrop.set_loaders(train_loader, val_loader) sbs_cnn2_nodrop.train(10)
1m25s



print( StepByStep.loader_apply(train_loader, sbs_cnn2_nodrop.correct).sum(axis=0), StepByStep.loader_apply(val_loader, sbs_cnn2_nodrop.correct).sum(axis=0) ) # tensor([2520, 2520]) tensor([293, 372])
That’s 100.00% accuracy on the training set! And 78.76% on the validation set—it smells like overfitting!
Then, let’s look at the regularized version of the model:
print( StepByStep.loader_apply(train_loader, sbs_cnn2.correct).sum(axis=0), StepByStep.loader_apply(val_loader, sbs_cnn2.correct).sum(axis=0) ) # tensor([2504, 2520]) tensor([327, 372])
That’s 99.37% accuracy on the training set—still quite high! But we got 87.90% on the validation set now—a narrower gap between training and validation accuracy is always a good sign. You can also try different probabilities of dropout and observe how much better (or worse!) the results get.

model_cnn2.conv1.weight.shape # torch.Size([5, 3, 3, 3])


Figure 6.12 - Visualizing filters for conv1 layer
For the second convolutional layer, conv2, we get:
model_cnn2.conv2.weight.shape # torch.Size([5, 5, 3, 3])

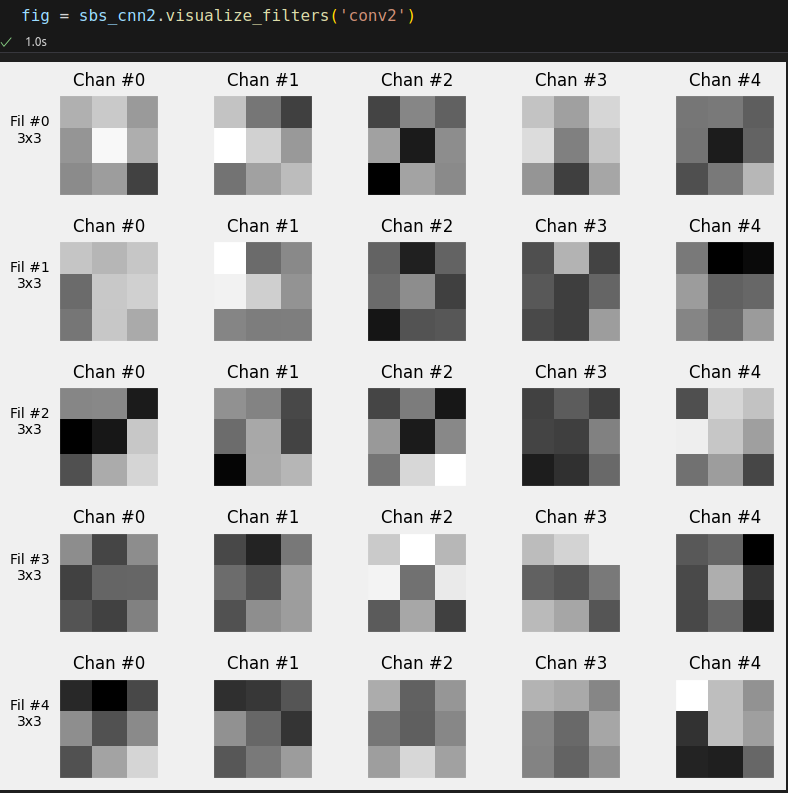
Figure 6.13 - Visualizing filters for conv2 layer




def make_lr_fn(start_lr, end_lr, n_iter, step_mode='exp'): if step_mode == 'linear': factor = (end_lr / start_lr - 1) / n_iter def lr_fn(iteration): return 1 + iteration * factor else: factor = (np.log(end_lr) - np.log(start_lr)) / n_iter def lr_fn(iteration): return np.exp(factor) ** iteration return lr_fn
Now, let’s try it out: Say we’d like to try ten different learning rates between 0.01 and 0.2, and the increments should be exponential:
start_lr = 0.01 end_lr = 0.2 n_iter = 10 lr_fn_exp = make_lr_fn(start_lr, end_lr, n_iter, step_mode='exp')
There is a factor of 20 between the two rates. If we apply this function to a sequence of iteration numbers, from 0 to 10, that’s what we get:
lr_fn_exp(np.arange(n_iter + 1))
array([ 1. , 1.34928285, 1.8205642 , 2.45645605, 3.31445402, 4.47213595, 6.03417634, 8.14181063, 10.98560543, 14.82268898, 20. ])
lr_fn_linear = make_lr_fn(start_lr, end_lr, n_iter, step_mode='linear') lr_fn_linear(np.arange(n_iter + 1))
array([ 1. , 2.9, 4.8, 6.7, 8.6, 10.5, 12.4, 14.3, 16.2, 18.1, 20. ])
If we multiply these values by the initial learning rate, we’ll get an array of learning rates ranging from 0.01 to 0.2 as expected:
start_lr * lr_fn_exp(np.arange(n_iter + 1))
array([0.01 , 0.01349283, 0.01820564, 0.02456456, 0.03314454, 0.04472136, 0.06034176, 0.08141811, 0.10985605, 0.14822689, 0.2 ])

start_lr = 0.01 end_lr = 0.1 n_iter = 10 lr_fn = make_lr_fn(start_lr, end_lr, n_iter, step_mode='exp') start_lr * lr_fn(np.arange(n_iter + 1))
array([0.01 , 0.01258925, 0.01584893, 0.01995262, 0.02511886, 0.03162278, 0.03981072, 0.05011872, 0.06309573, 0.07943282, 0.1 ])
from torch.optim.lr_scheduler import LambdaLR dummy_model = CNN2(n_feature=5, p=.3) dummy_optimizer = optim.Adam(dummy_model.parameters(), lr=start_lr) dummy_lr_scheduler = LambdaLR(dummy_optimizer, lr_lambda=lr_fn)

dummy_optimizer.step()
dummy_lr_scheduler.step()

dummy_lr_scheduler.get_last_lr() # [np.float64(0.012589254117941673)]

def lr_range_test(self, data_loader, end_lr, n_iter=100, step_mode='exp', alpha=.05, ax=None): # Since the test updates both model and optimizer we need to store # their initial states to restore them in the end previous_states = {'model': deepcopy(self.model.state_dict()), 'optimizer': deepcopy(self.optimizer.state_dict())} # Retrieve the learning rate set in the optimizer start_lr = self.optimizer.state_dict()['param_groups'][0]['lr'] # Build a custom function and corresponding scheduler lr_fn = make_lr_fn(start_lr, end_lr, n_iter) scheduler = LambdaLR(self.optimizer, lr_lambda=lr_fn) # Variables for tracking results and iterations tracking = {'loss': [], 'lr': []} iteration = 0 # If there are more iterations than mini-batches in the data loader, # it will have to loop over it more than once while iteration < n_iter: # That's the typical mini-batch inner loop for x_batch, y_batch in data_loader: x_batch = x_batch.to(self.device) y_batch = y_batch.to(self.device) # Step 1 yhat = self.model(x_batch) # Step 2 loss = self.loss_fn(yhat, y_batch) # Step 3 loss.backward() # Here we keep track of the losses (smoothed) and the learning rates tracking['lr'].append(scheduler.get_last_lr()[0]) if iteration == 0: tracking['loss'].append(loss.item()) else: prev_loss = tracking['loss'][-1] smoothed_loss = alpha * loss.item() + (1 - alpha) * prev_loss tracking['loss'].append(smoothed_loss) iteration += 1 if iteration == n_iter: break # Step 4 self.optimizer.step() scheduler.step() self.optimizer.zero_grad() # Restore the original states self.model.load_state_dict(previous_states['model']) self.optimizer.load_state_dict(previous_states['optimizer']) if ax is None: fig, ax = plt.subplots(1, 1, figsize=(6, 4)) else: fig = ax.get_figure() ax.set_xlabel('Learning Rate') ax.set_ylabel('Loss') if step_mode == 'exp': ax.set_xscale('log') ax.plot(tracking['lr'], tracking['loss']) fig.tight_layout() return tracking, fig

lr = 0.0003 torch.manual_seed(13) new_model = CNN2(n_feature=5, p=0.3) ce_loss_fn = nn.CrossEntropyLoss(reduction='mean') new_optimizer = optim.Adam(new_model.parameters(), lr=lr)

sbs_new = StepByStep(new_model, ce_loss_fn, new_optimizer)
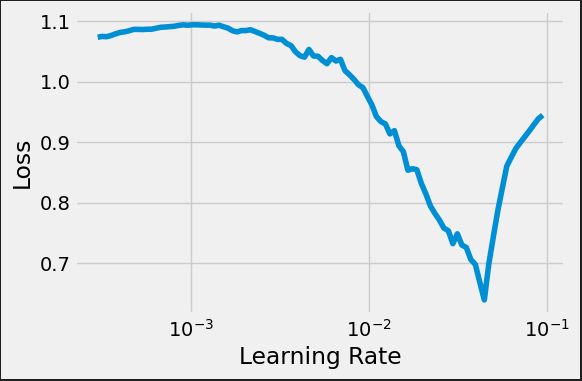
tracking, fig = sbs_new.lr_range_test(train_loader, end_lr=.1, n_iter=100)


![]()

def set_optimizer(self, optimizer):
self.optimizer = optimizer
Then, we create and set the new optimizer and train the model as usual:
new_optimizer = optim.Adam(new_model.parameters(), lr=.005)
sbs_new.set_optimizer(new_optimizer)
sbs_new.set_loaders(train_loader, val_loader)
sbs_new.train(20)
If you try it out, you’ll find that the training loss actually goes down a bit faster (and that the model might be overfitting).


https://pypi.org/project/torch-lr-finder/
%pip install --quiet torch-lr-finder
from torch_lr_finder import LRFinder
Note: you may need to restart the kernel to use updated packages. /zdata/Github/zpytorch/lib/python3.12/site-packages/torch_lr_finder/lr_finder.py:5: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html from tqdm.autonotebook import tqdm
zzh@ZZHPC:~$ pip list | grep torch_lr_finder
(zpytorch) zzh@ZZHPC:~/zd/Github$ pip list | grep torch_lr_finder

fig, ax = plt.subplots(1, 1, figsize=(6, 4))
torch.manual_seed(11)
new_model = CNN2(n_feature=5, p=0.3)
ce_loss_fn = nn.CrossEntropyLoss(reduction='mean')
new_optimizer = optim.Adam(new_model.parameters(), lr=0.0003)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
lr_finder = LRFinder(new_model, new_optimizer, ce_loss_fn, device)
lr_finder.range_test(train_loader, end_lr=0.1, num_iter=100)
lr_finder.plot(ax=ax, log_lr=True)
fig.tight_layout()
lr_finder.reset()
Learning rate search finished. See the graph with {finder_name}.plot()
LR suggestion: steepest gradient
Suggested LR: 1.01E-02

Not quite a "U" shape, but we still can tell that something in the ballpark of 1e-2 is a good starting point.


 EWMA
EWMA


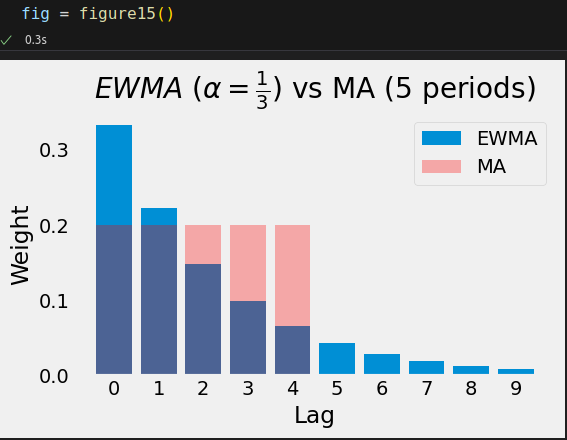

alpha = 1/3; T = 94 avg_age_EWMA = .0 for t in range(1, T + 1): lag = t - 1 avg_age_EWMA += alpha * ((1 - alpha) ** lag * (lag + 1)) if t < 20 or t > 80: print(avg_age_EWMA) if t == 20: print('...')
0.3333333333333333
0.7777777777777778
1.2222222222222223
1.617283950617284
1.946502057613169
2.209876543209877
2.4147233653406497
2.5707971345831435
2.6878524615150137
2.7745601110941767
2.838145720785563
2.884389800561117
2.917788302621239
2.9417667143567114
2.9588941513106204
2.9710736620334
2.979700815462036
2.9857905708234256
2.990075954225885
...
2.9999999999995444
2.9999999999996936
2.999999999999794
2.999999999999862
2.9999999999999076
2.9999999999999387
2.9999999999999596
2.999999999999974
2.999999999999983
2.9999999999999893
2.999999999999994
2.999999999999997
2.9999999999999987
3.0

In code, the implementation of the alpha version of EWMA looks like this:
def EWMA(past_value, current_value, alpha): return alpha * current_value + (1 - alpha) * past_value
For computing it over a series of values, given a period, we can define a function like this:
def calc_ewma(values, period): alpha = 2 / (period + 1) result = [] for v in values: try: prev_value = result[-1] except IndexError: prev_value = 0 new_value = EWMA(prev_value, v, alpha=alpha) result.append(new_value) return np.array(result)
In the try..except block, you can see that, if there is no previous value for the EWMA (as in the very first step), it assumes a previous value of zero.
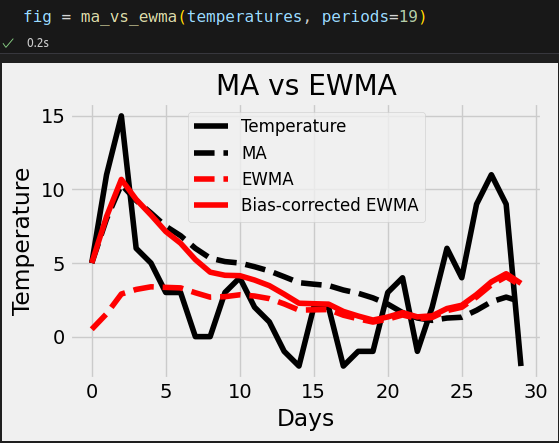
The way the EWMA is constructed has its issues—since it does not need to keep track of all the values inside its period, in its first steps, the "average" will be way off (or biased). For an alpha=0.1 (corresponding to the 19-periods average), the very first "average" will be exactly the first value times 0.1.

def correction(averaged_value, beta, step): ''' Parameters: averaged_value: the EWMA value needs to be corrected beta: 1 - alpha step: 1 for the first value, 2 for the second value, and so on ''' return averaged_value / (1 - beta ** step)
For computing the corrected EWMA over a series of values, we can use a function like this:
def calc_corrected_ewma(values, period): ewma = calc_ewma(values, period) alpha = 2 / (period + 1) beta = 1 - alpha result = [correction(v, beta, i + 1) for i, v in enumerate(ewma)] return np.array(result)
Let’s apply both EWMAs, together with a regular moving average, to a sequence of temperature values to illustrate the differences:
temperatures = np.array([5, 11, 15, 6, 5, 3, 3, 0, 0, 3, 4, 2, 1, -1, -2, 2, 2, -2, -1, -1, 3, 4, -1, 2, 6, 4, 9, 11, 9, -2]) temperatures.shape # (30,)




optimizer = optim.Adam(model_cnn2.parameters(), lr=0.0125, betas=(0.9, 0.999), eps=1e-8)

%run -i data_generation/simple_linear_regression.py
%run -i data_preparation/v2.py
Then, we go over the model configuration and change the optimizer from SGD to Adam:
torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(1, 1)) optimizer = optim.Adam(model.parameters(), lr=.1) loss_fn = nn.MSELoss(reduction='mean')


self._gradients = {} def capture_gradients(self, layers_to_hook): modules = list(self.model.named_modules()) module_names = [name for name, layer in modules] if layers_to_hook is None: layers_to_hook = module_names[1:] else: layers_to_hook = [layers_to_hook] if isinstance(layers_to_hook, str) else list(layers_to_hook) self._gradients = {} def make_log_fn(name, parm_id): def log_fn(grad): self._gradients[name][parm_id].append(grad.tolist()) return return log_fn for name, layer in modules: if name in layers_to_hook: self._gradients.update({name: {}}) for parm_id, p in layer.named_parameters(): if p.requires_grad: self._gradients[name].update({parm_id: []}) log_fn = make_log_fn(name, parm_id) self.handles[f'{name}.{parm_id}.grad'] = p.register_hook(log_fn) return

Now, we can use the new method to log gradients for the linear layer of our model, never forgetting to remove the hooks after training:
sbs_adam = StepByStep(model, loss_fn, optimizer) sbs_adam.set_loaders(train_loader, val_loader) sbs_adam.capture_gradients('linear') sbs_adam.train(10) sbs_adam.remove_hooks()


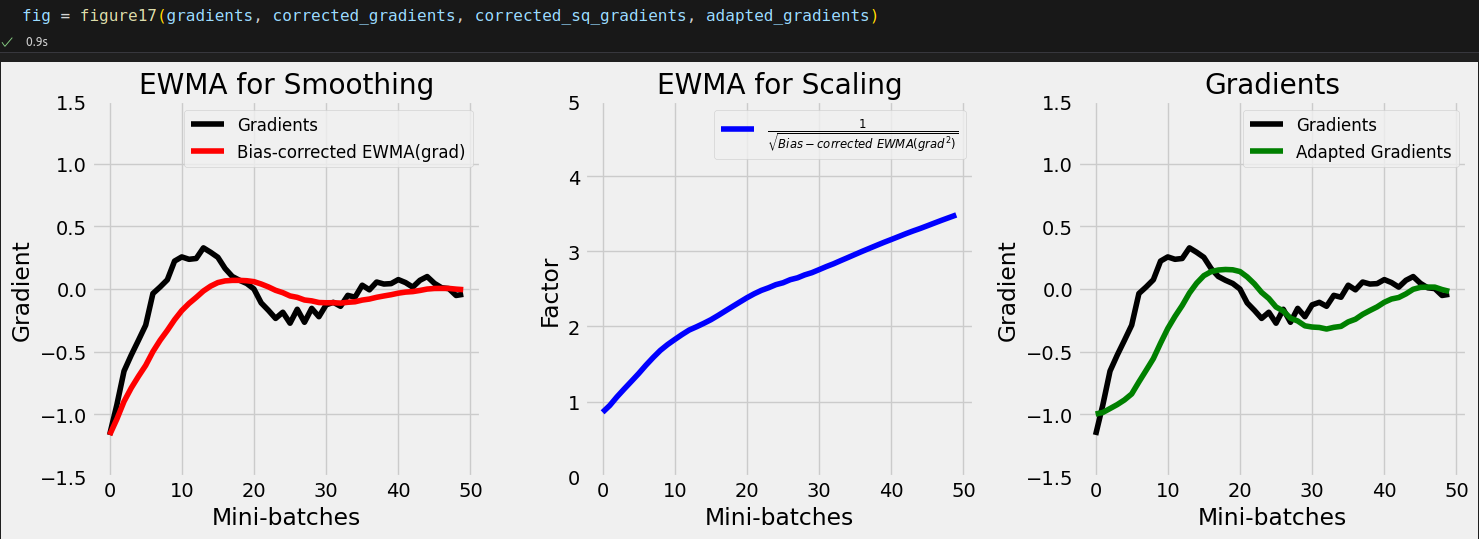
gradients = np.array(sbs_adam._gradients['linear']['weight']).squeeze() corrected_gradients = calc_corrected_ewma(gradients, 19) corrected_sq_gradients = calc_corrected_ewma(np.power(gradients, 2), 1999) adapted_gradients = corrected_gradients / (np.sqrt(corrected_sq_gradients) + 1e-8)

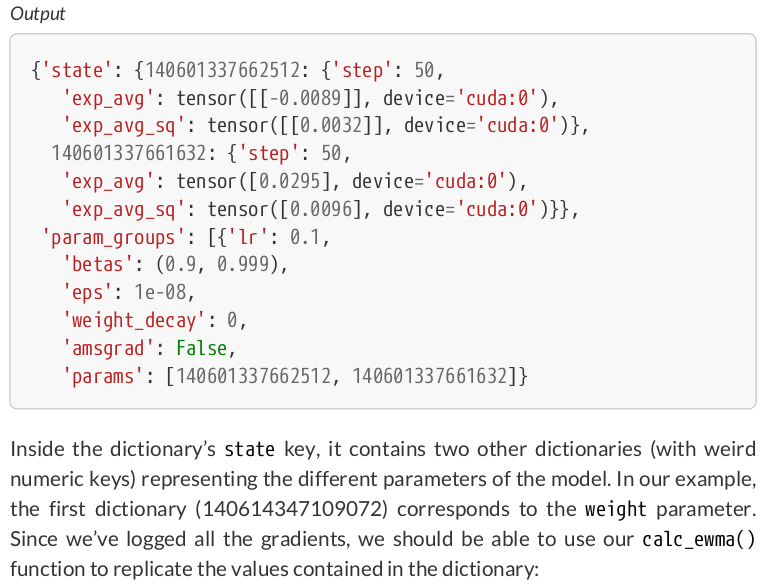
optimizer.state_dict()
{'state': {0: {'step': tensor(50.),
'exp_avg': tensor([[-0.0055]], device='cuda:0'),
'exp_avg_sq': tensor([[0.0040]], device='cuda:0')},
1: {'step': tensor(50.),
'exp_avg': tensor([0.0525], device='cuda:0'),
'exp_avg_sq': tensor([0.0104], device='cuda:0')}},
'param_groups': [{'lr': 0.1,
'betas': (0.9, 0.999),
'eps': 1e-08,
'weight_decay': 0,
'amsgrad': False,
'maximize': False,
'foreach': None,
'capturable': False,
'differentiable': False,
'fused': None,
'params': [0, 1]}]}
model.state_dict()
OrderedDict([('linear.weight', tensor([[1.9344]], device='cuda:0')), ('linear.bias', tensor([1.0099], device='cuda:0'))])
calc_ewma(gradients, 19)[-1], calc_ewma(np.power(gradients, 2), 1999)[-1] # (np.float64(-0.005502247372857658), np.float64(0.004014803099570996))


self._parameters = {} def capture_parameters(self, layers_to_hook): modules = list(self.model.named_modules()) layer_names = {layer: name for name, layer in modules} if layers_to_hook is None: layers_to_hook = list(layer_names.values())[1:] else: layers_to_hook = [layers_to_hook] if isinstance(layers_to_hook, str) else list(layers_to_hook) self._parameters = {} for name, layer in modules: if name in layers_to_hook: self._parameters.update({name: {}}) for parm_id, p in layer.named_parameters(): self._parameters[name].update({parm_id: []}) def fw_hook_fn(layer, inputs, outputs): name = layer_names[layer] for parm_id, p in layer.named_parameters(): self._parameters[name][parm_id].append(p.tolist()) self.attach_hooks(layers_to_hook, fw_hook_fn) return
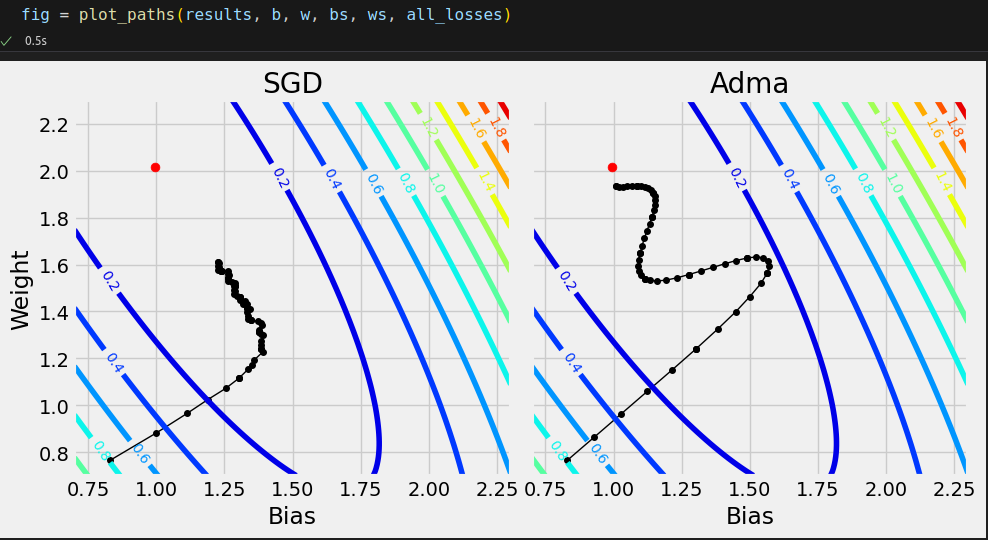
What’s next? We need to create two instances of StepByStep, each using a different optimizer, set them to capture parameters, and train them for ten epochs. The captured parameters (bias and weight) will draw the following paths (the red dot represents their optimal values).
def compare_optimizers(model, loss_fn, optimizers, train_loader, val_loader=None, schedulers=None, layers_to_hook=None, n_epochs=50): results = {} model_state = deepcopy(model.state_dict()) for desc, options in optimizers.items(): model.load_state_dict(model_state) optimizer = options['class'](model.parameters(), **options['parms']) sbs = StepByStep(model, loss_fn, optimizer) sbs.set_loaders(train_loader, val_loader) try: if schedulers is not None: sched = schedulers[desc] scheduler = sched['class'](optimizer, **sched['parms']) sbs.set_lr_scheduler(scheduler) except KeyError: pass sbs.capture_parameters(layers_to_hook) sbs.capture_gradients(layers_to_hook) sbs.train(n_epochs) sbs.remove_hooks() parms = deepcopy(sbs._parameters) grads = deepcopy(sbs._gradients) lrs = sbs.learning_rates[:] if not lrs: lrs = [list(map(lambda p: p['lr'], optimizer.state_dict()['param_groups']))] * n_epochs results.update({desc: {'parms': parms, 'grads': grads, 'losses': np.array(sbs.losses), 'val_losses': np.array(sbs.val_losses), 'state': optimizer.state_dict(), 'lrs': lrs}}) return results
# Generating data for the plots torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(1, 1)) loss_fn = nn.MSELoss(reduction='mean') optimizers = {'SGD': {'class': optim.SGD, 'parms': {'lr': .1}}, 'Adma': {'class': optim.Adam, 'parms': {'lr': .1}}} results = compare_optimizers(model, loss_fn, optimizers, train_loader, val_loader, layers_to_hook='linear', n_epochs=10) b, w, bs, ws, all_losses = contour_data(x_tensor, y_tensor)
def plot_paths(results, b, w, bs, ws, all_losses, axs=None): if axs is None: fig, axs = plt.subplots(1, len(results), figsize=(5 * len(results), 5)) axs = np.atleast_2d(axs) axs = [ax for row in axs for ax in row] for i, (ax, desc) in enumerate(zip(axs, results.keys())): biases = np.array(results[desc]['parms']['linear']['bias']).squeeze() weights = np.array(results[desc]['parms']['linear']['weight']).squeeze() ax.set_title(desc) ax.set_xlabel('Bias') ax.set_ylabel('Weight') ax.set_xlim([.7, 2.3]) ax.set_ylim([.7, 2.3]) ax.plot(biases, weights, '-o', linewidth=1, zorder=1, c='k', markersize=4) ax.scatter(b, w, c='r', zorder=2, s=40) # Loss surface CS = ax.contour(bs[0, :], ws[:, 0], all_losses, cmap=plt.cm.jet, levels=12) ax.clabel(CS, inline=1, fontsize=10) ax.label_outer() fig = ax.get_figure() fig.tight_layout() return fig

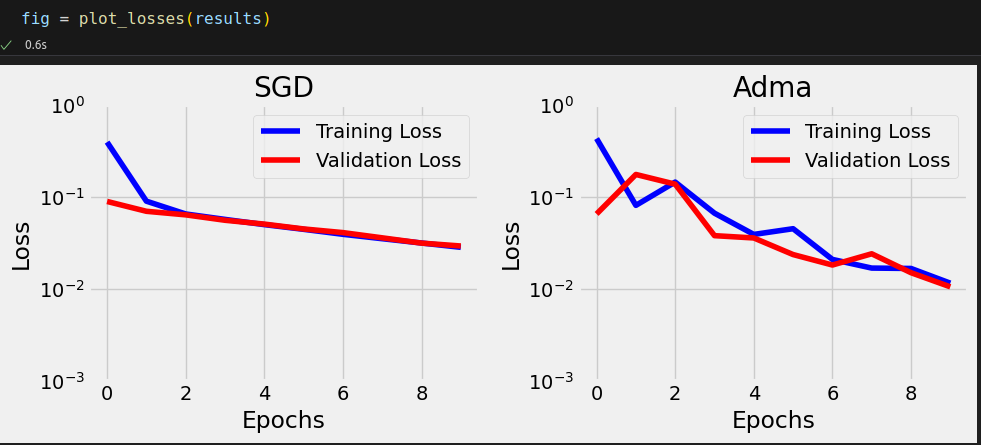
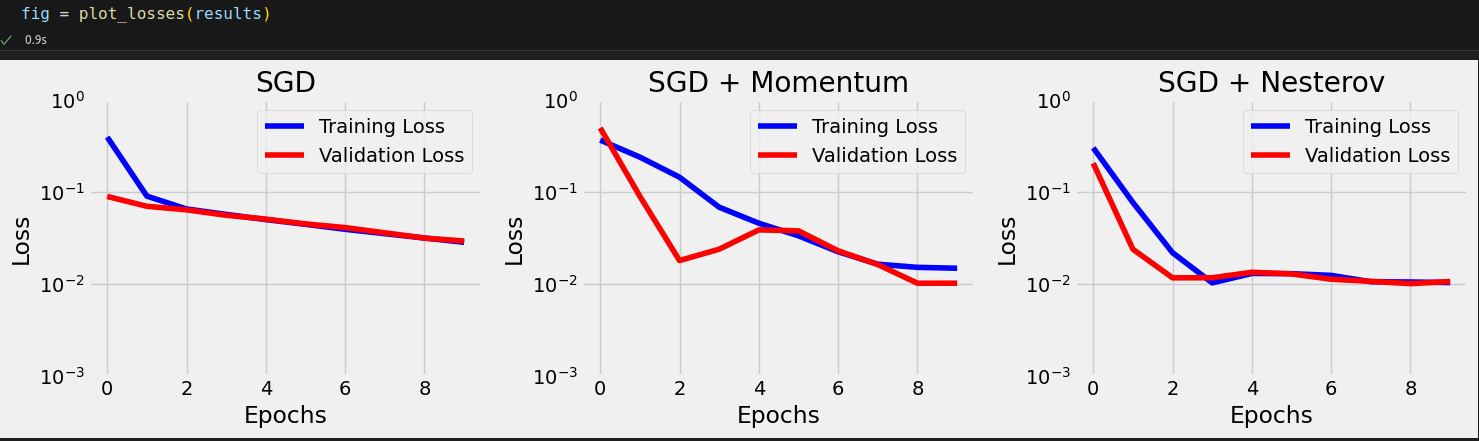
Talking about losses, we can also compare the trajectories of training and validation losses for each optimizer.



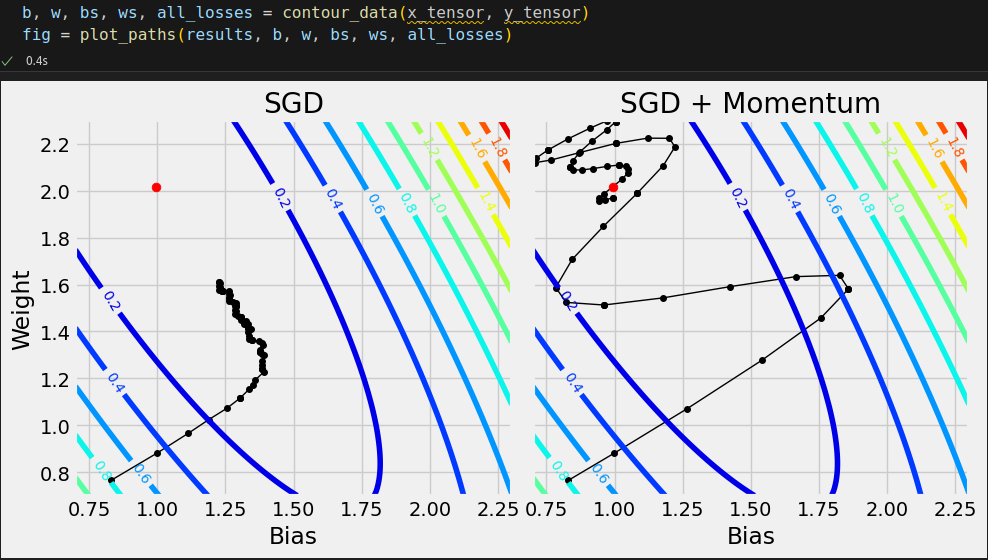
# Generating data for the plots torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(1, 1)) loss_fn = nn.MSELoss(reduction='mean') optimizers = {'SGD': {'class': optim.SGD, 'parms': {'lr': 0.1}}, 'SGD + Momentum': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9}}} results = compare_optimizers(model, loss_fn, optimizers, train_loader, val_loader, layers_to_hook='linear', n_epochs=10) results['SGD + Momentum']['state']
{'state': {0: {'momentum_buffer': tensor([[-0.1137]], device='cuda:0')},
1: {'momentum_buffer': tensor([-0.3048], device='cuda:0')}},
'param_groups': [{'lr': 0.1,
'momentum': 0.9,
'dampening': 0,
'weight_decay': 0,
'nesterov': False,
'maximize': False,
'foreach': None,
'differentiable': False,
'fused': None,
'params': [0, 1]}]}







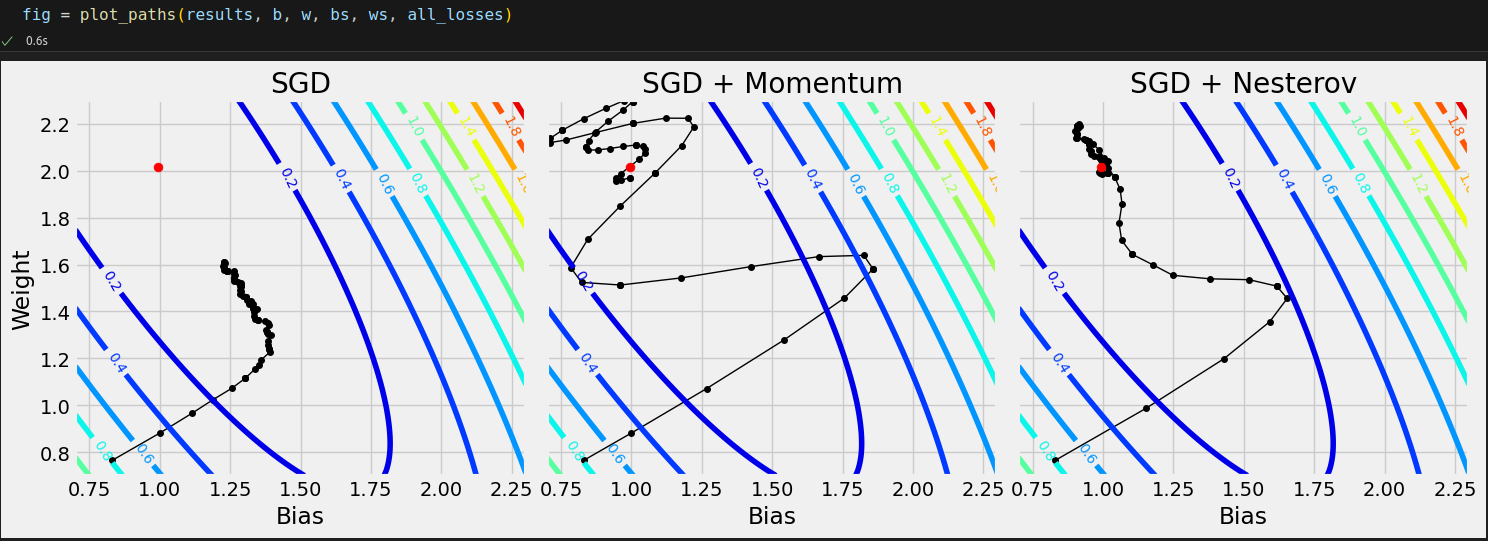
# Generating data for the plots torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(1, 1)) loss_fn = nn.MSELoss(reduction='mean') optimizers = {'SGD': {'class': optim.SGD, 'parms': {'lr': .1}}, 'SGD + Momentum': {'class': optim.SGD, 'parms': {'lr': .1, 'momentum': .9}}, 'SGD + Nesterov': {'class': optim.SGD, 'parms': {'lr': .1, 'momentum': .9, 'nesterov': True}}} results = compare_optimizers(model, loss_fn, optimizers, train_loader, val_loader, layers_to_hook='linear', n_epochs=10)





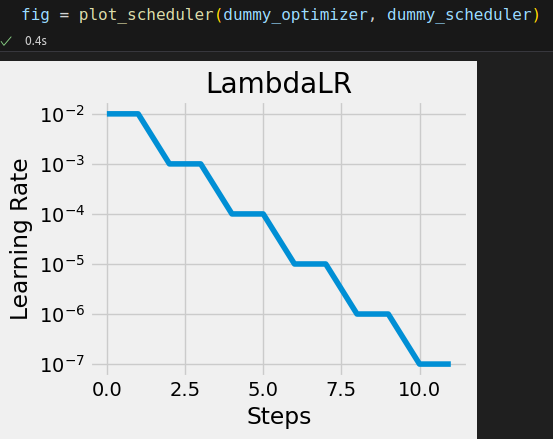
from torch.optim.lr_scheduler import StepLR dummy_optimizer = optim.SGD([nn.Parameter(torch.randn(1))], lr=0.01) dummy_scheduler = StepLR(dummy_optimizer, step_size=2, gamma=0.1)

for epoch in range(4): # trainin loop code goes here print(dummy_scheduler.get_last_lr()) # First call optimizer's step dummy_optimizer.step() # Then call scheduler's step dummy_scheduler.step() dummy_optimizer.zero_grad()
[0.01] [0.01] [0.001] [0.001]


We can use LambdaLR to mimic the behavior of the StepLR scheduler defined above:
dummy_optimizer = optim.SGD([nn.Parameter(torch.randn(1))], lr=0.01) dummy_scheduler = LambdaLR(dummy_optimizer, lr_lambda=lambda epoch: 0.1 ** (epoch // 2)) # The scheduler above is equivalent to this one # dummy_scheduler = StepLR(dummy_optimizer, step_size=2, gamma=0.1)


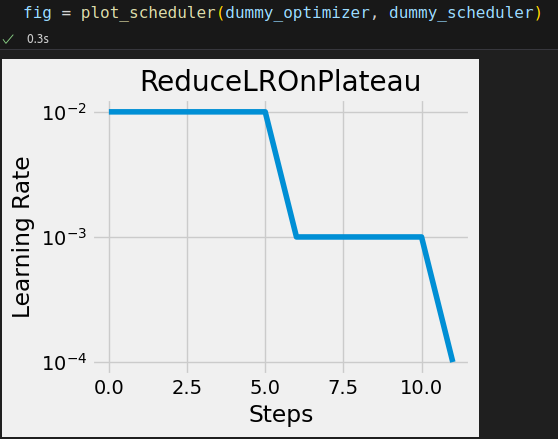
from torch.optim.lr_scheduler import ReduceLROnPlateau dummy_optimizer = optim.SGD([nn.Parameter(torch.randn(1))], lr=0.01) dummy_scheduler = ReduceLROnPlateau(dummy_optimizer, patience=4, factor=0.1)


self.scheduler = None self.is_batch_lr_scheduler = False def set_lr_scheduler(self, scheduler): # Make sure the scheduler in the argument is assigned to the optimizer we're using in this class if scheduler.optimizer == self.optimizer: self.scheduler = scheduler if (isinstance(scheduler, CyclicLR) or isinstance(scheduler, OneCycleLR) or isinstance(scheduler, CosineAnnealingWarmRestarts)): self.is_batch_lr_scheduler = True

def _epoch_schedulers(self, metrics): if self.scheduler: if not self.is_batch_lr_scheduler: if isinstance(self.scheduler, ReduceLROnPlateau): self.scheduler.step(metrics) else: self.scheduler.step() current_lr = list(map(lambda osd_pgs: osd_pgs['lr'], self.scheduler.optimizer.state_dict()['param_groups'])) self.learning_rates.append(current_lr)
And then we modify the train() method to include a call to the protected method defined above. It should come after the validation inner loop.
def train(self, n_epochs, seed=42): self.set_seed(seed) for epoch in range(n_epochs): # Keep track of the numbers of epochs by updating the corresponding attribute self.total_epochs += 1 loss = self._mini_batch(validation=False) self.losses.append(loss) with torch.no_grad(): val_loss = self._mini_batch(validation=True) self.val_losses.append(val_loss) # Call the learning rate scheduler self._epoch_schedulers(val_loss) # If a SummaryWriter has been set... if self.writer: scalars = {'training': loss} if val_loss is not None: scalars.update({'validation': val_loss}) self.writer.add_scalars(main_tag='loss', tag_scalar_dict=scalars, global_step=epoch) if self.writer: # Flush the writer self.writer.flush()

dummy_parm = [nn.Parameter(torch.randn(1))] dummy_optimizer = optim.SGD(dummy_parm, lr=0.01) dummy_scheduler1 = CyclicLR(dummy_optimizer, base_lr=1e-4, max_lr=1e-3, step_size_up=2, mode='triangular') dummy_scheduler2 = CyclicLR(dummy_optimizer, base_lr=1e-4, max_lr=1e-3, step_size_up=2, mode='triangular2') dummy_scheduler3 = CyclicLR(dummy_optimizer, base_lr=1e-4, max_lr=1e-3, step_size_up=2, mode='exp_range', gamma=np.sqrt(0.5))
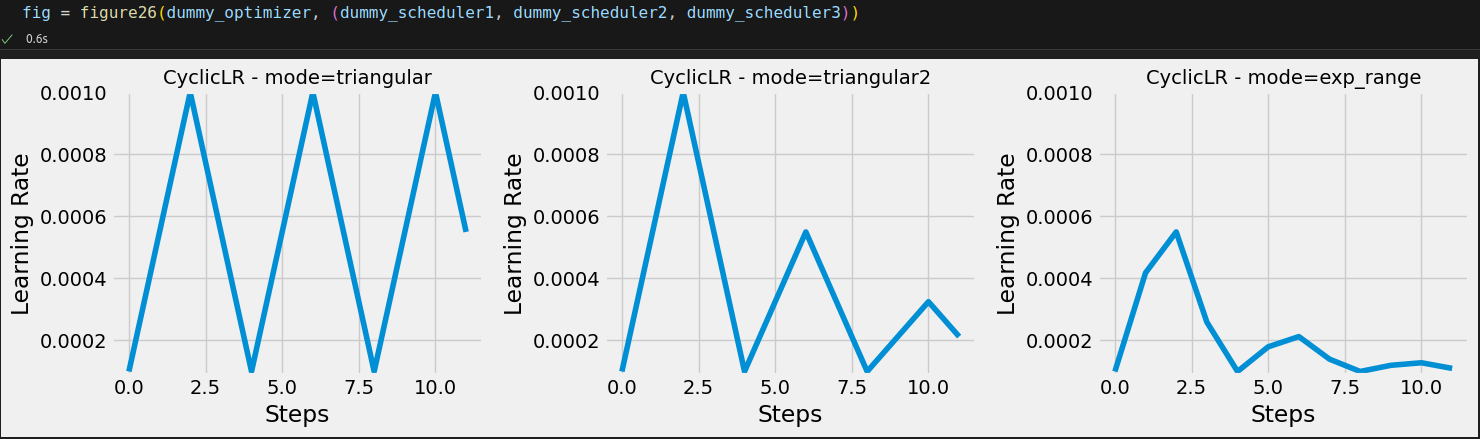


def _mini_batch_schedulers(self, frac_epoch): if self.scheduler: if self.is_batch_lr_scheduler: if isinstance(self.scheduler, CosineAnnealingWarmRestarts): self.scheduler.step(self.total_epochs + frac_epoch) else: self.scheduler.step() current_lr = list(map(lambda osd_pgs: osd_pgs['lr'], self.scheduler.optimizer.state_dict()['param_groups'])) self.learning_rates.append(current_lr)

def _mini_batch(self, validation=False): # The mini-batch can be used with both loaders # The argument `validation` defines which loader and # corresponding step function is going to be used if validation: data_loader = self.val_loader step_fn = self.val_step_fn else: data_loader = self.train_loader step_fn = self.train_step_fn if data_loader is None: return None n_batches = len(data_loader) mini_batch_losses = [] for i, (x_batch, y_batch) in enumerate(data_loader): x_batch = x_batch.to(self.device) y_batch = y_batch.to(self.device) mini_batch_loss = step_fn(x_batch, y_batch) mini_batch_losses.append(mini_batch_loss) # Only during training! if not validation: # Call the learning rate scheduler at the end of every mini-batch update self._mini_batch_schedulers(i / n_batches) loss = np.mean(mini_batch_losses) return loss

fig, axs = plt.subplots(1, 2, figsize=(10, 4)) for ax, nesterov in zip(axs.flat, [False, True]): torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(1, 1)) loss_fn = nn.MSELoss(reduction='mean') optimizer = optim.SGD(model.parameters(), lr=1e-3, momentum=0.9, nesterov=nesterov) sbs_scheduler = StepByStep(model, loss_fn, optimizer) tracking, fig = sbs_scheduler.lr_range_test(train_loader, end_lr=1, n_iter=100, ax=ax) nest = ' + Nesterov' if nesterov else '' ax.set_title(f'Momentum{nest}')
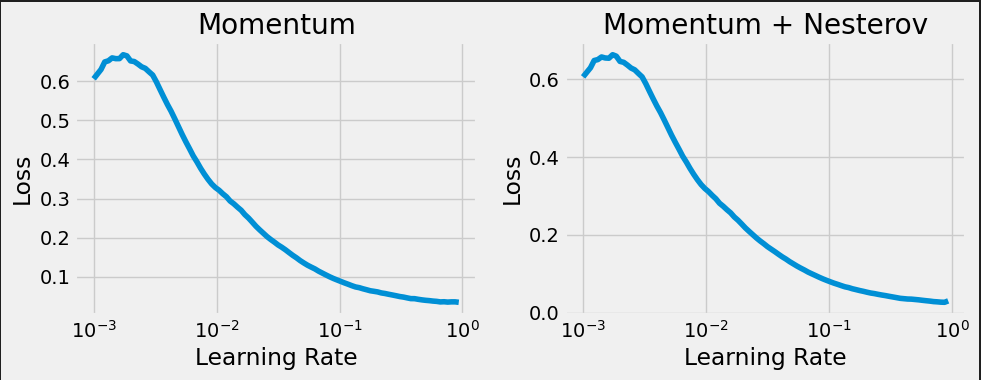

Let’s be bold! First, we define the optimizer with our choice for initial learning rate (0.1).

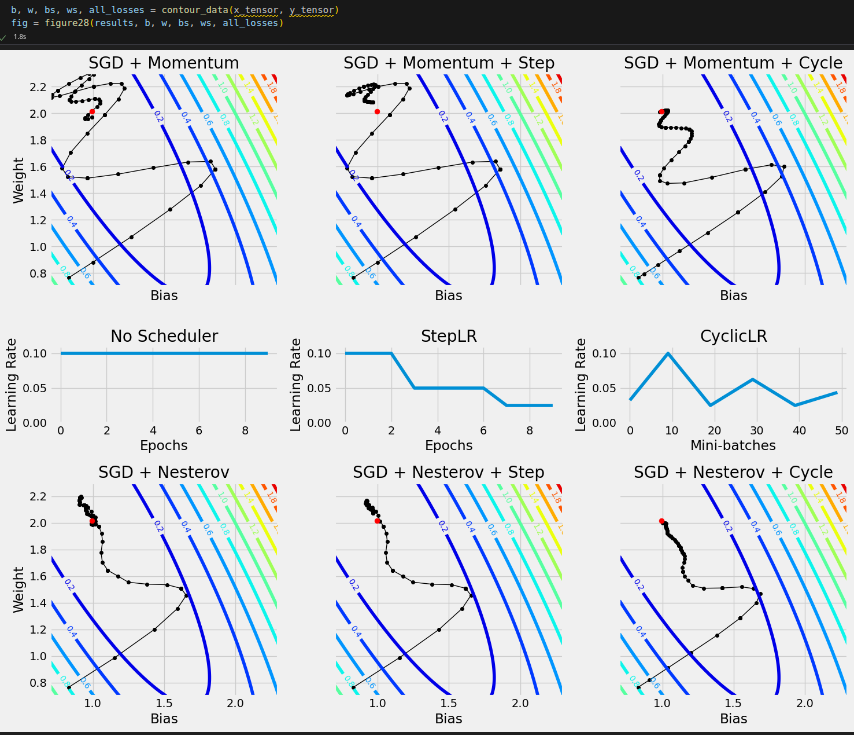
# Generating data for the plots torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(1, 1)) loss_fn = nn.MSELoss(reduction='mean') optimizers = {'SGD + Momentum': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9}}, 'SGD + Momentum + Step': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9}}, 'SGD + Momentum + Cycle': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9}}, 'SGD + Nesterov': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9, 'nesterov': True}}, 'SGD + Nesterov + Step': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9, 'nesterov': True}}, 'SGD + Nesterov + Cycle': {'class': optim.SGD, 'parms': {'lr': 0.1, 'momentum': 0.9, 'nesterov': True}}} schedulers = {'SGD + Momentum + Step': {'class': StepLR, 'parms': {'step_size': 4, 'gamma': 0.5}}, 'SGD + Momentum + Cycle': {'class': CyclicLR, 'parms': {'base_lr': 0.025, 'max_lr': 0.1, 'step_size_up': 10, 'mode': 'triangular2'}}, 'SGD + Nesterov + Step': {'class': StepLR, 'parms': {'step_size': 4, 'gamma': 0.5}}, 'SGD + Nesterov + Cycle': {'class': CyclicLR, 'parms': {'base_lr': 0.025, 'max_lr': 0.1, 'step_size_up': 10, 'mode': 'triangular2'}}} results = compare_optimizers(model, loss_fn, optimizers, train_loader, val_loader, schedulers, n_epochs=10)
After applying each scheduler to SGD with momentum, and to SGD with Nesterov’s momentum, we obtain the following paths:




# Load temporary dataset to build normalizer temp_transform = Compose([Resize(28), ToImage(), ToDtype(torch.float32, scale=True)]) temp_dataset = ImageFolder(root='rps', transform=temp_transform) temp_loader = DataLoader(temp_dataset, batch_size=16) normalizer = StepByStep.make_normalizer(temp_loader) # Build transformation, datasets and data loaders composer = Compose([Resize(28), ToImage(), ToDtype(torch.float32, scale=True), normalizer]) train_data = ImageFolder(root='rps', transform=composer) val_data = ImageFolder(root='rps-test-set', transform=composer) # Build a loader of each set train_loader = DataLoader(train_data, batch_size=16, shuffle=True) val_loader = DataLoader(val_data, batch_size=16)
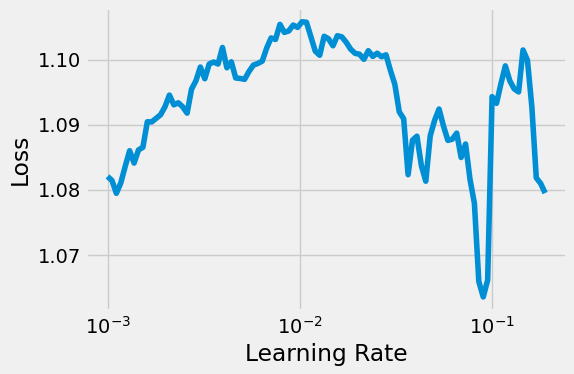
torch.manual_seed(13) model_cnn3 = CNN2(n_feature=5, p=0.5) ce_loss_fn = nn.CrossEntropyLoss(reduction='mean') optimizer_cnn3 = optim.SGD(model_cnn3.parameters(), lr=1e-3, momentum=0.9, nesterov=True)
sbs_cnn3 = StepByStep(model_cnn3, ce_loss_fn, optimizer_cnn3)
tracking, fig = sbs_cnn3.lr_range_test(train_loader, end_lr=2e-1, n_iter=100)
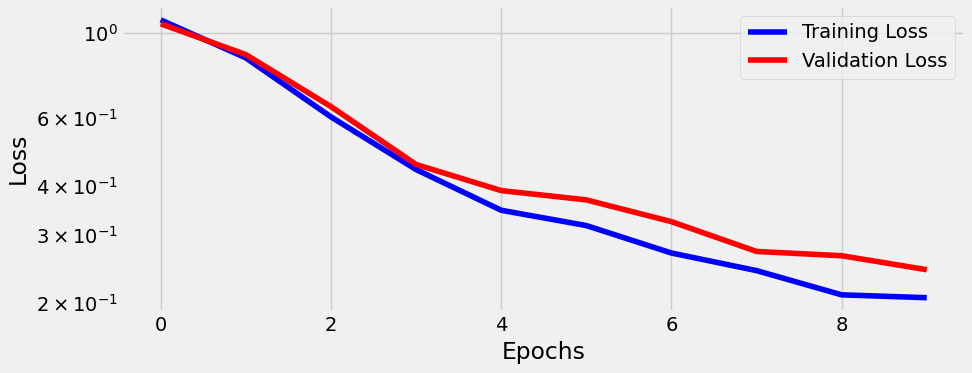
optimizer_cnn3 = optim.SGD(model_cnn3.parameters(), lr=0.01, momentum=0.9, nesterov=True) sbs_cnn3.set_optimizer(optimizer_cnn3) scheduler = CyclicLR(optimizer_cnn3, base_lr=1e-3, max_lr=0.01, step_size_up=len(train_loader), mode='triangular2') sbs_cnn3.set_lr_scheduler(scheduler)
sbs_cnn3.set_loaders(train_loader, val_loader)
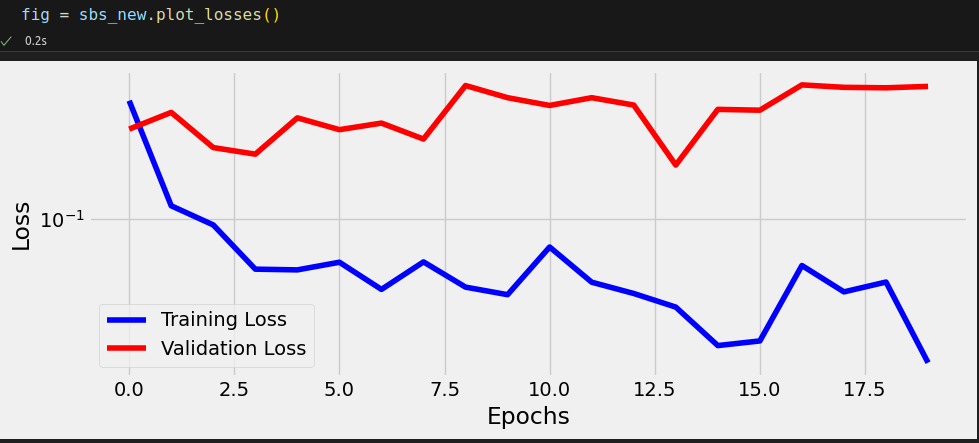
sbs_cnn3.train(10)
fig = sbs_cnn3.plot_losses()
print(StepByStep.loader_apply(train_loader, sbs_cnn3.correct).sum(axis=0), StepByStep.loader_apply(val_loader, sbs_cnn3.correct).sum(axis=0)) # tensor([2504, 2520]) tensor([336, 372])



 浙公网安备 33010602011771号
浙公网安备 33010602011771号