

from sklearn.datasets import make_moons from sklearn.model_selection import train_test_split X, y = make_moons(n_samples=100, noise=.3, random_state=0) X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=.2, random_state=13)



from sklearn.preprocessing import StandardScaler sc = StandardScaler() sc.fit(X_train) X_train = sc.transform(X_train) X_val = sc.transform(X_val)



torch.manual_seed(13) # Build tensors from numpy arrays x_train_tensor = torch.as_tensor(X_train).float() y_train_tensor = torch.as_tensor(y_train.reshape(-1, 1)).float() x_val_tensor = torch.as_tensor(X_val).float() y_val_tensor = torch.as_tensor(y_val.reshape(-1, 1)).float() # Build datasets train_dataset = TensorDataset(x_train_tensor, y_train_tensor) val_dataset = TensorDataset(x_val_tensor, y_val_tensor) # Build data loaders train_loader = DataLoader(dataset=train_dataset, batch_size=16, shuffle=True) val_loader = DataLoader(dataset=val_dataset, batch_size=16)






def odds_ratio(prob): return prob / (1 - prob) p = .75 q = 1 - p odds_ratio(p), odds_ratio(q) # (3.0, 0.3333333333333333)





def log_odds_ratio(prob): return np.log(odds_ratio(prob)) p = .75 q = 1 - p log_odds_ratio(p), log_odds_ratio(q) # (np.float64(1.0986122886681098), np.float64(-1.0986122886681098))





def sigmoid(z): return 1 / (1 + np.exp(-z)) p = .75 q = 1 - p sigmoid(log_odds_ratio(p)), sigmoid(log_odds_ratio(q)) # (np.float64(0.75), np.float64(0.25))

torch.sigmoid(torch.tensor(1.0986)), torch.sigmoid(torch.tensor(-1.0986)) # (tensor(0.7500), tensor(0.2500))






torch.manual_seed(42) model1 = nn.Sequential() model1.add_module('linear', nn.Linear(2, 1)) model1.add_module('sigmoid', nn.Sigmoid()) print(model1.state_dict()) # OrderedDict({'linear.weight': tensor([[0.5406, 0.5869]]), 'linear.bias': tensor([-0.1657])})



dummy_labels = torch.tensor([1., .0]) dummy_predictions = torch.tensor([.9, .2]) # Positive class (labels == 1) pos_pred = dummy_predictions[dummy_labels == 1] first_summation = torch.log(pos_pred).sum() # Negative class (labels == 0) neg_pred = dummy_predictions[dummy_labels == 0] second_summation = torch.log(1 - neg_pred).sum() # n_total = n_pos + n_neg n_total = dummy_labels.size(0) loss = -(first_summation + second_summation) / n_total loss # tensor(0.1643)

summation = torch.sum(dummy_labels * torch.log(dummy_predictions) + (1 - dummy_labels) * torch.log(1 - dummy_predictions)) loss = -summation / n_total loss # tensor(0.1643)



loss_fn = nn.BCELoss(reduction='mean') loss_fn # BCELoss()


loss = loss_fn(dummy_predictions, dummy_labels) loss # tensor(0.1643)




loss_fn_logits = nn.BCEWithLogitsLoss(reduction='mean') loss_fn_logits # BCEWithLogitsLoss()

logit1 = log_odds_ratio(.9) logit2 = log_odds_ratio(.2) dummy_logits = torch.tensor([logit1, logit2]) print(dummy_logits) # tensor([ 2.1972, -1.3863], dtype=torch.float64)
We have logits, and we have labels. Time to compute the loss:
loss = loss_fn_logits(dummy_logits, dummy_labels) loss # tensor(0.1643)
OK, we got the same result, as expected.


n_neg = (dummy_imb_labels == 0).sum() n_pos = (dummy_imb_labels == 1).sum() pos_weight = (n_neg / n_pos).view(1,) pos_weight # tensor([3.])
Now, let’s create yet another loss function, including the pos_weight argument this time:
loss_fn_imb = nn.BCEWithLogitsLoss(reduction='mean', pos_weight=pos_weight) loss = loss_fn_imb(dummy_imb_logits, dummy_imb_labels) loss # tensor(0.2464)



loss_fn_imb_sum = nn.BCEWithLogitsLoss(reduction='sum', pos_weight=pos_weight) loss = loss_fn_imb_sum(dummy_imb_logits, dummy_imb_labels) loss = loss / (pos_weight * n_pos + n_neg) loss # tensor([0.1643])
There we go!

This is what the model configuration looks like for our classification problem:
lr = .1 torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(2, 1)) optimizer = optim.SGD(model.parameters(), lr=lr) loss_fn = nn.BCEWithLogitsLoss()

epochs = 100 sbs = StepByStep(model, loss_fn, optimizer) sbs.set_loaders(train_loader, val_loader) sbs.train(epochs)


print(model.state_dict()) # OrderedDict({'linear.weight': tensor([[ 1.1806, -1.8693]], device='cuda:0'), 'linear.bias': tensor([-0.0591], device='cuda:0')})


predictions = sbs.predict(x_train_tensor[:4]) predictions # array([[ 0.20345594], # [ 2.9444456 ], # [ 3.693318 ], # [-1.2334074 ]], dtype=float32)

probabilities = sigmoid(predictions) probabilities # array([[0.5506892], # [0.9500003], # [0.9757152], # [0.2255856]], dtype=float32)

classes = (predictions >= 0).astype(int) classes # array([[1], # [1], # [1], # [0]])



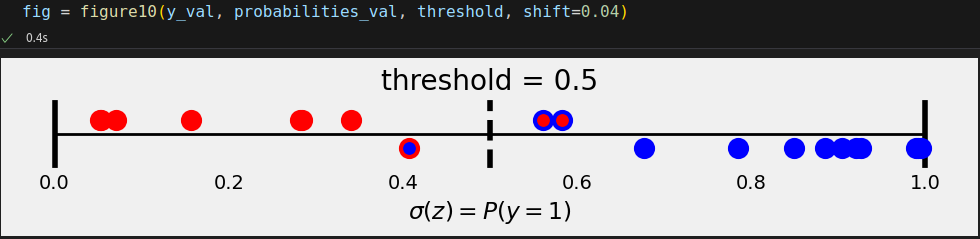
An image is worth a thousand words, right? Let’s plot it!












First, let’s compute the logits and corresponding probabilities:
logits_val = sbs.predict(X_val) probabilities_val = sigmoid(logits_val).squeeze() threshold = .5



It looks like this:
 Confusion Matrix
Confusion Matrix


from sklearn.metrics import confusion_matrix cm_threshold50 = confusion_matrix(y_val, (probabilities_val >= .5)) cm_threshold50 # array([[ 7, 2], # [ 1, 10]])

def split_cm(cm): # Actual negatives go in the top row, above the probability line actual_negative = cm[0] # Predicted negatives go in the first column tn = actual_negative[0] # Predicted positives go in the second column fp = actual_negative[1] # Actual positives go in the bottow row, below the probability line actual_positive = cm[1] # Predicted negatives go in the first column fn = actual_positive[0] # Predicted positives go in the second column tp = actual_positive[1] return tn, fp, fn, tp


def tpr_fpr(cm): tn, fp, fn, tp = split_cm(cm) tpr = tp / (tp + fn) fpr = fp / (fp + tn) return tpr, fpr
tpr_fpr(cm_threshold50) # (np.float64(0.9090909090909091), np.float64(0.2222222222222222))

 recall, precision
recall, precision
def precision_recall(cm): tn, fp, fn, tp = split_cm(cm) precision = tp / (tp + fp) recall = tp / (tp + fn) return precision, recall
precision_recall(cm_threshold50) # (np.float64(0.8333333333333334), np.float64(0.9090909090909091))

 accuracy
accuracy
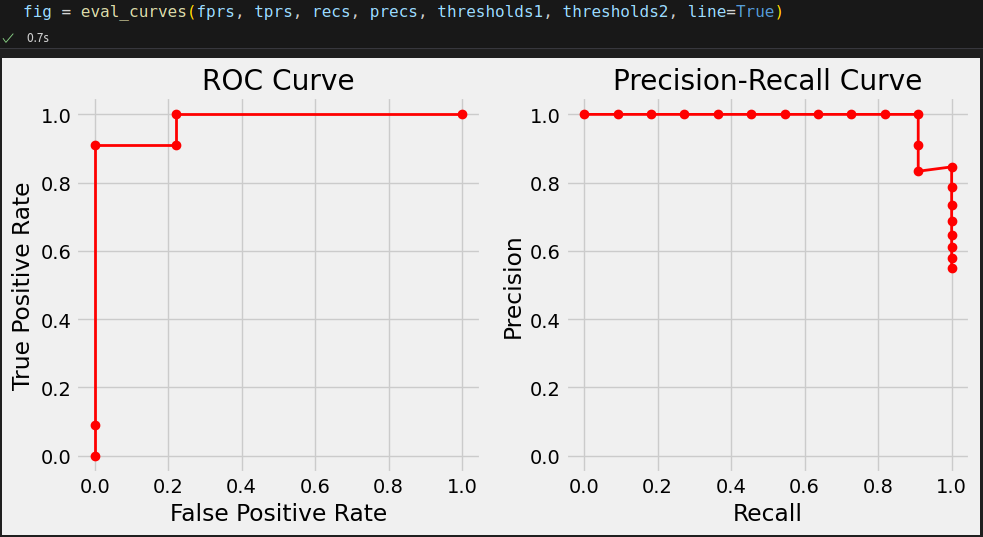
 ROC Curve, PR Curve
ROC Curve, PR Curve




confusion_matrix(y_val, (probabilities_val >= 0.3)) # array([[ 6, 3], # [ 0, 11]])
OK, now let’s plot the corresponding metrics one more time:





confusion_matrix(y_val, (probabilities_val >= 0.7)) # array([[9, 0], # [2, 9]])
OK, now let’s plot the corresponding metrics again:





from sklearn.metrics import roc_curve, precision_recall_curve fprs, tprs, thresholds1 = roc_curve(y_val, probabilities_val) precs, recs, thresholds2 = precision_recall_curve(y_val, probabilities_val)








rng = np.random.default_rng(39) random_probs = rng.standard_normal(y_val.shape) fprs_random, tprs_random, thresholds1_random = roc_curve(y_val, random_probs) precs_random, recs_random, thresholds2_random = precision_recall_curve(y_val, random_probs)



from sklearn.metrics import auc # Area under the curves of our model auroc = auc(fprs, tprs) aupr = auc(recs, precs) print(auroc, aupr) # 0.9797979797979798 0.9854312354312356

# Area under the curves of the random model auroc_random = auc(fprs_random, tprs_random) aupr_random = auc(recs_random, precs_random) print(auroc_random, aupr_random) # 0.5252525252525253 0.540114743045365
Close enough; after all, the curves produced by our random model were only roughly approximating the theoretical ones.

torch.manual_seed(13) # Build tensors from numpy arrays x_train_tensor = torch.as_tensor(X_train).float() y_train_tensor = torch.as_tensor(y_train.reshape(-1, 1)).float() x_val_tensor = torch.as_tensor(X_val).float() y_val_tensor = torch.as_tensor(y_val.reshape(-1, 1)).float() # Build datasets train_dataset = TensorDataset(x_train_tensor, y_train_tensor) val_dataset = TensorDataset(x_val_tensor, y_val_tensor) # Build data loaders train_loader = DataLoader(dataset=train_dataset, batch_size=16, shuffle=True) val_loader = DataLoader(dataset=val_dataset, batch_size=16)
lr = .1 torch.manual_seed(42) model = nn.Sequential() model.add_module('linear', nn.Linear(2, 1)) optimizer = optim.SGD(model.parameters(), lr=lr) loss_fn = nn.BCEWithLogitsLoss()
epochs = 100 sbs = StepByStep(model, loss_fn, optimizer) sbs.set_loaders(train_loader, val_loader) sbs.train(epochs)
print(model.state_dict())
logits_val = sbs.predict(X_val) probabilities_val = sigmoid(logits_val).squeeze() cm_thresh50 = confusion_matrix(y_val, (probabilities_val >= 0.5)) cm_thresh50






