Regression is a statistical technique that relates a dependent variable to one or more independent variables.
A regression model is able to show whether changes observed in the dependent variable are associated with changes in one or more of the independent variables.




# Step 0 - Initialize parameters 'b' and 'w' randomly rng = np.random.default_rng() b = rng.random(1)[0] w = rng.random(1)[0] print(f'Initial: {b = :.4f}, {w = :.4f}') # Set learning rate, this is "eta" lr = 0.1 # Set number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train # Step 2 - Compute the loss error = yhat - y_train loss = (error ** 2).mean() # Step 3 - Compute gradients for both 'b' and 'w' parameters grad_b = 2 * error.mean() grad_w = 2 * (x_train * error).mean() # Step 4 - Update parameters using gradients and the learning rate b = b - lr * grad_b w = w - lr * grad_w if epoch < 15 or (epoch + 1) % 100 == 0 and (epoch + 1) % 1000 !=0: print(f'{epoch + 1}th update: {b = :.4f}, {w = :.4f}') print(f'Final: {b = :.4f}, {w = :.4f}')
Initial: b = 0.4906, w = 0.0505 1th update: b = 0.8038, w = 0.2507 2th update: b = 1.0327, w = 0.4020 3th update: b = 1.1993, w = 0.5173 4th update: b = 1.3202, w = 0.6058 5th update: b = 1.4072, w = 0.6747 6th update: b = 1.4694, w = 0.7289 7th update: b = 1.5133, w = 0.7724 8th update: b = 1.5437, w = 0.8079 9th update: b = 1.5641, w = 0.8374 10th update: b = 1.5773, w = 0.8625 11th update: b = 1.5851, w = 0.8843 12th update: b = 1.5889, w = 0.9037 13th update: b = 1.5899, w = 0.9212 14th update: b = 1.5888, w = 0.9372 15th update: b = 1.5862, w = 0.9522 100th update: b = 1.2212, w = 1.6143 200th update: b = 1.0729, w = 1.8713 300th update: b = 1.0285, w = 1.9483 400th update: b = 1.0152, w = 1.9714 500th update: b = 1.0112, w = 1.9784 600th update: b = 1.0100, w = 1.9804 700th update: b = 1.0096, w = 1.9810 800th update: b = 1.0095, w = 1.9812 900th update: b = 1.0095, w = 1.9813 Final: b = 1.0095, w = 1.9813
Initial: b = 0.563431, w = 0.677705 1th update: b = 0.781718, w = 0.808832 2th update: b = 0.943310, w = 0.909453 3th update: b = 1.062579, w = 0.987253 4th update: b = 1.150258, w = 1.047971 5th update: b = 1.214365, w = 1.095895 6th update: b = 1.260885, w = 1.134228 7th update: b = 1.294290, w = 1.165362 8th update: b = 1.317918, w = 1.191085 9th update: b = 1.334263, w = 1.212731 10th update: b = 1.345187, w = 1.231300 11th update: b = 1.352079, w = 1.247536 12th update: b = 1.355979, w = 1.261996 13th update: b = 1.357661, w = 1.275098 14th update: b = 1.357704, w = 1.287153 15th update: b = 1.356540, w = 1.298395 100th update: b = 1.124938, w = 1.758428 200th update: b = 1.045570, w = 1.906913 300th update: b = 1.026159, w = 1.943228 400th update: b = 1.021411, w = 1.952110 500th update: b = 1.020250, w = 1.954282 600th update: b = 1.019966, w = 1.954813 700th update: b = 1.019897, w = 1.954943 800th update: b = 1.019880, w = 1.954975 900th update: b = 1.019876, w = 1.954983 Final: b = 1.019875, w = 1.954985
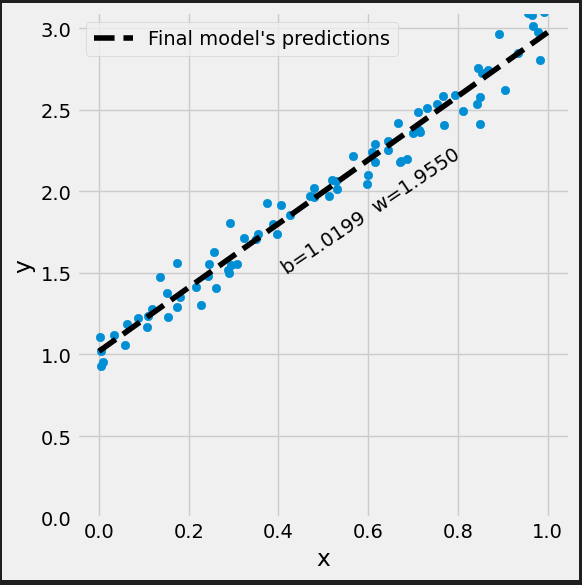


from sklearn.linear_model import LinearRegression # Sanity Check: do we get the same results as our gradient descent? linr = LinearRegression() linr.fit(x_train.reshape(-1, 1), y_train) print(linr.intercept_, linr.coef_[0]) # 1.019874488290637 1.9549854662785073








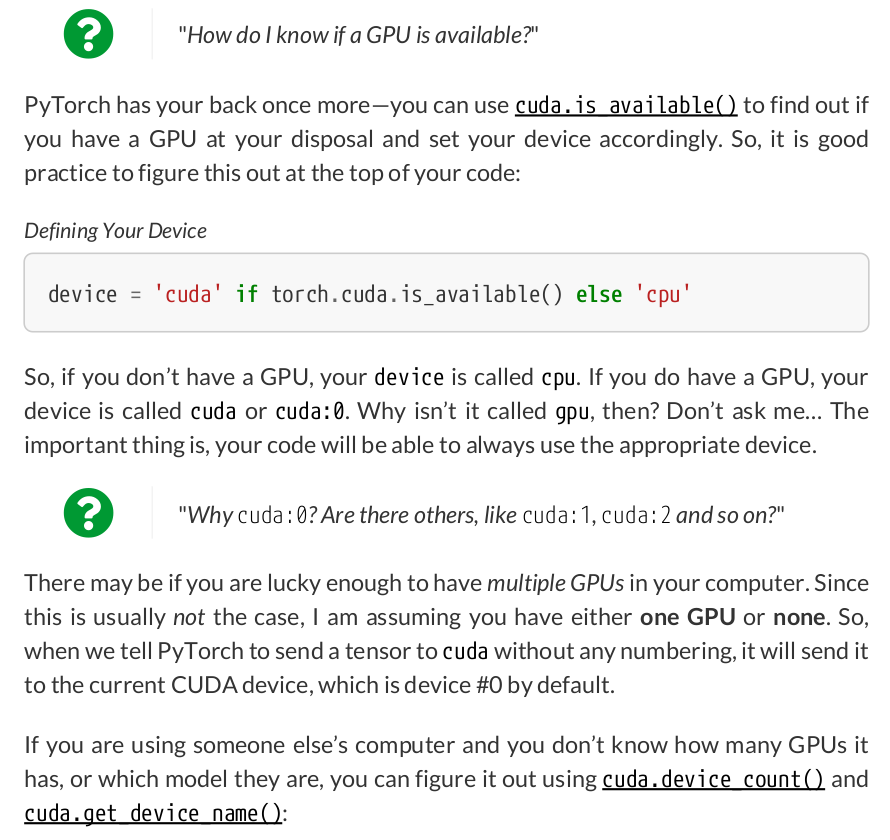
n_cudas = torch.cuda.device_count() for i in range(n_cudas): print(torch.cuda.get_device_name(i)) # NVIDIA GeForce RTX 2070

gpu_tensor = torch.as_tensor(x_train).to(device) gpu_tensor[0] # tensor(0.6432, device='cuda:0', dtype=torch.float64)
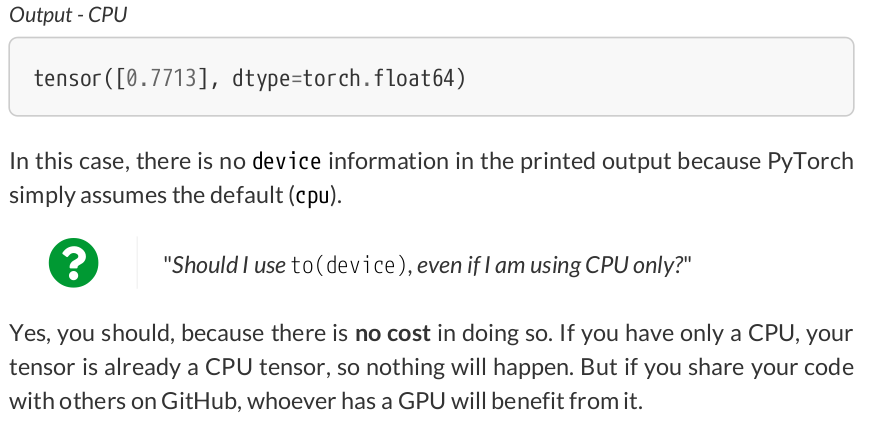

device = 'cuda' if torch.cuda.is_available() else 'cpu' # Our data was in Numpy arrays, but we need to transform them into PyTorch's Tensors # and then we send them to the chosen device. x_train_tensor = torch.as_tensor(x_train).float().to(device) y_train_tensor = torch.as_tensor(y_train).float().to(device)

# Here we can see the difference - notice that .type() is more # useful since it also tells us WHERE the tensor is (device) print(type(x_train), type(x_train_tensor), x_train_tensor.type()) # <class 'numpy.ndarray'> <class 'torch.Tensor'> torch.cuda.FloatTensor
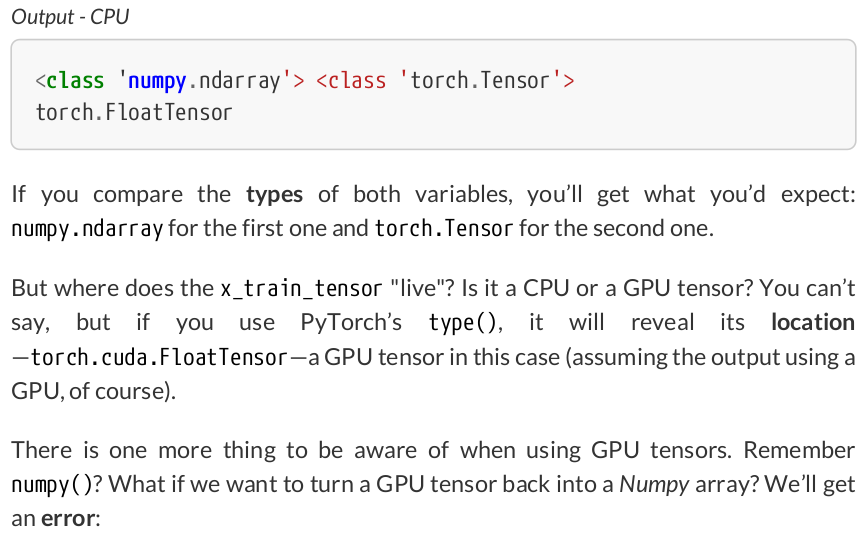






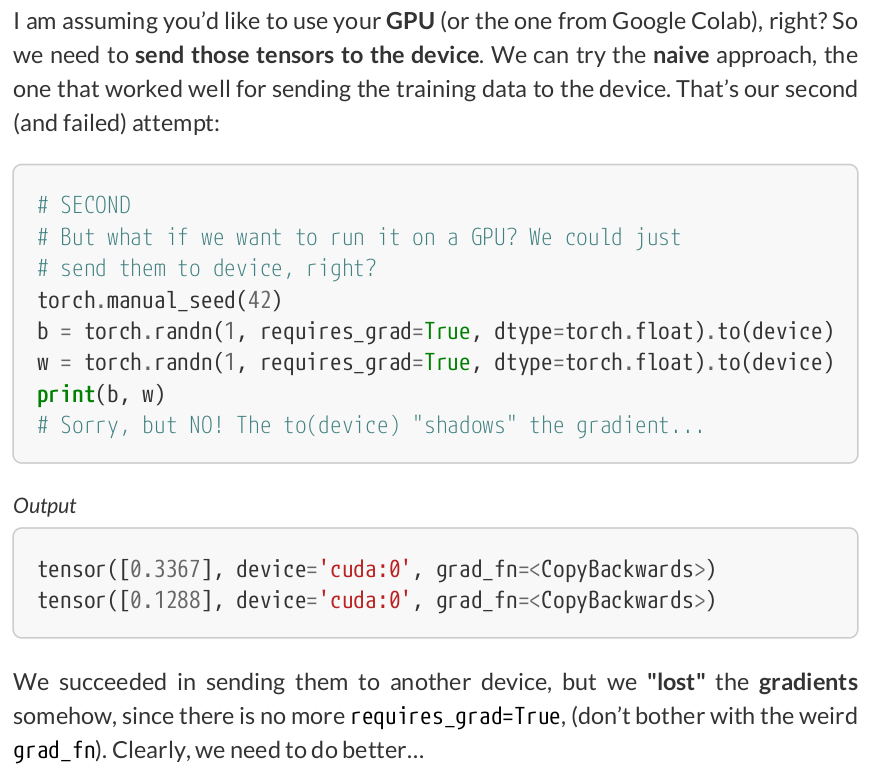

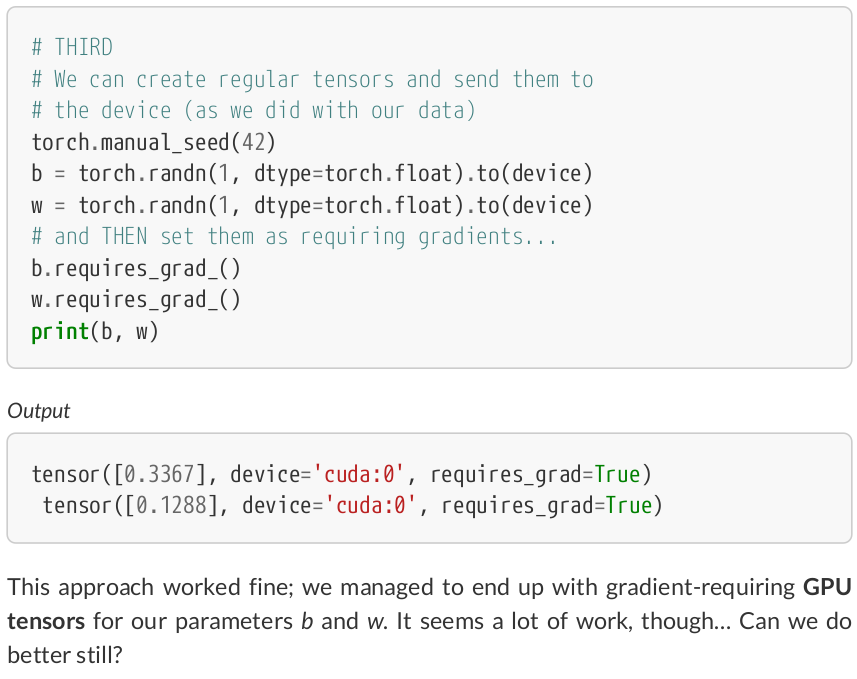

# FINAL # We can specify the device at the moment of creation # RECOMMENDED! # Step 0 - Initialize parameters "b" and "w" randomly torch.manual_seed(42) b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) w = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) print(b, w) # tensor([0.1940], device='cuda:0', requires_grad=True) # tensor([0.1391], device='cuda:0', requires_grad=True)

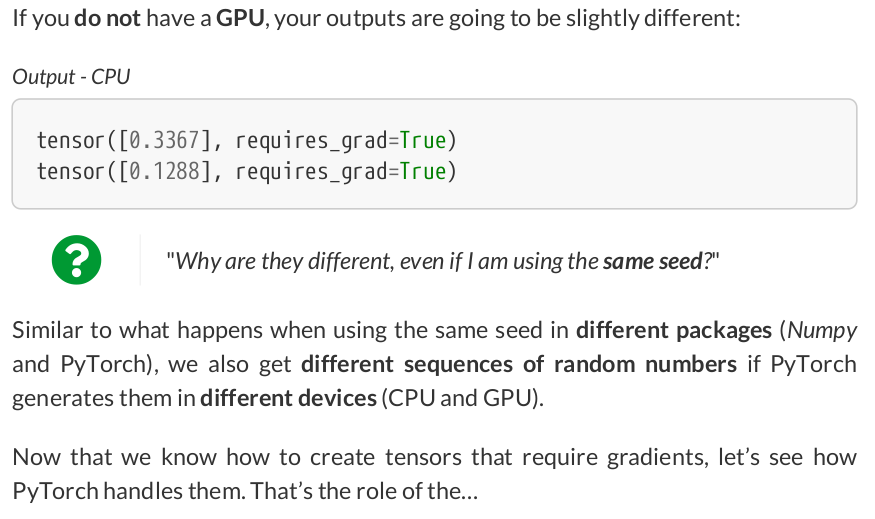


# Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train_tensor # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent error = yhat - y_train_tensor loss = (error ** 2).mean() # MSE # Step 3 - Compute gradients for both "b" and "w" parameters # No more manual computation of gradients! loss.backward()


print(b.grad) # tensor([-3.3892], device='cuda:0') print(w.grad) # tensor([-1.9051], device='cuda:0')

print(b.grad) # tensor([-6.7783], device='cuda:0') print(w.grad) # tensor([-3.8102], device='cuda:0')


# This code will be placed *after* Step 4 (updating the parameters) b.grad.zero_(), w.grad.zero_() # (tensor([0.], device='cuda:0'), tensor([0.], device='cuda:0'))

# Set learning rate - this is eta lr = 0.1 # Step 0 - Initialize parameters "b" and "w" randomly torch.manual_seed(42) b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) w = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) # Number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train_tensor # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. error = yhat - y_train_tensor loss = (error ** 2).mean() # MSE # Step 3 - Compute gradients for both "b" and "w" parameters # We just tell PyTorch to work its way BACKWARDS from the specified loss! loss.backward() print(f'{epoch=}') print(b.grad) print(b.grad) # Step 4 - Update parameters using gradients and the learning rate # FIRST ATTEMPT - just using the same code as before b = b - lr * b.grad w = w - lr * w.grad
epoch=0
tensor([-3.4540], device='cuda:0')
tensor([-3.4540], device='cuda:0')
epoch=1
None
None
/tmp/ipykernel_8404/734752770.py:26: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten/src/ATen/core/TensorBody.h:489.)
print(b.grad)
/tmp/ipykernel_8404/734752770.py:27: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten/src/ATen/core/TensorBody.h:489.)
print(b.grad)
/tmp/ipykernel_8404/734752770.py:31: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten/src/ATen/core/TensorBody.h:489.)
b = b - lr * b.grad
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[26], line 31
27 print(b.grad)
29 # Step 4 - Updates parameters using gradients and the learning rate
30 # FIRST ATTEMPT - just using the same code as before
---> 31 b = b - lr * b.grad
32 w = w - lr * w.grad
TypeError: unsupported operand type(s) for *: 'float' and 'NoneType'
# SECOND ATTEMPT - using in-place Python assigment b -= lr * b.grad w -= lr * w.grad
epoch=0
tensor([-3.4540], device='cuda:0')
tensor([-3.4540], device='cuda:0')
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
Cell In[27], line 36
27 print(b.grad)
29 # Step 4 - Updates parameters using gradients and the learning rate
30 # FIRST ATTEMPT - just using the same code as before
31 # TypeError: unsupported operand type(s) for *: 'float' and 'NoneType'
(...)
34
35 # SECOND ATTEMPT - using in-place Python assigment
---> 36 b -= lr * b.grad
37 w -= lr * w.grad
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
# Set learning rate - this is eta lr = 0.1 # Step 0 - Initialize parameters "b" and "w" randomly torch.manual_seed(42) b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) w = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) # Number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train_tensor # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. error = yhat - y_train_tensor loss = (error ** 2).mean() # MSE # Step 3 - Compute gradients for both "b" and "w" parameters # We just tell PyTorch to work its way BACKWARDS from the specified loss! loss.backward() # Step 4 - Updates parameters using gradients and the learning rate # FIRST ATTEMPT - just using the same code as before # TypeError: unsupported operand type(s) for *: 'float' and 'NoneType' # b = b - lr * b.grad # w = w - lr * w.grad # SECOND ATTEMPT - using in-place Python assigment # RuntimeError: a leaf Variable that requires grad is being used in an in-place operation. # b -= lr * b.grad # w -= lr * w.grad # THIRD ATTEMPT - NO_GRAD for the win! # We need to use NO_GRAD to keep the update out of the gradient computation. # Why is that? It boils down to the DYNAMIC GRAPH that PyTorch uses... with torch.no_grad(): b -= lr * b.grad w -= lr * w.grad # PyTorch is "clingy" to its computed gradients, we need to tell it to let it go... b.grad.zero_() w.grad.zero_() print(b) print(w)
tensor([0.9719], device='cuda:0', requires_grad=True) tensor([2.0522], device='cuda:0', requires_grad=True)




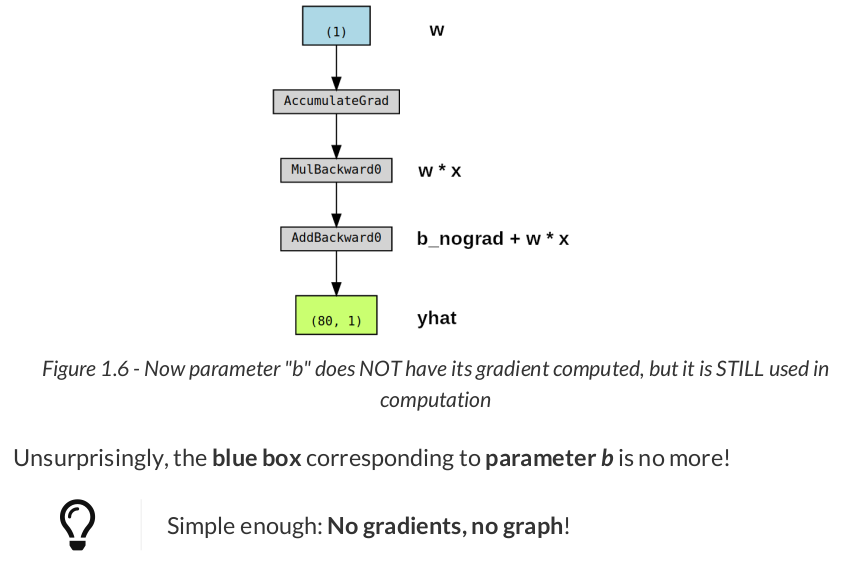
# Step 0 - Initializes parameters "b" and "w" randomly torch.manual_seed(42) b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) w = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) # Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train_tensor # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. error = yhat - y_train_tensor loss = (error ** 2).mean() # MSE # We can try plotting the graph for any python variable: # yhat, error, loss... make_dot(yhat) # from torchviz import make_dot
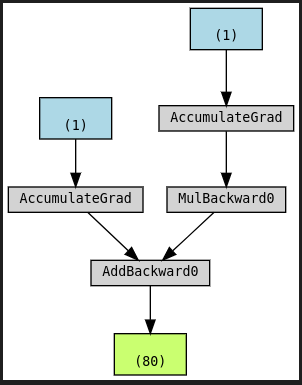
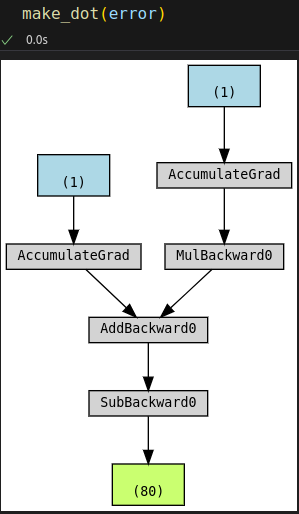
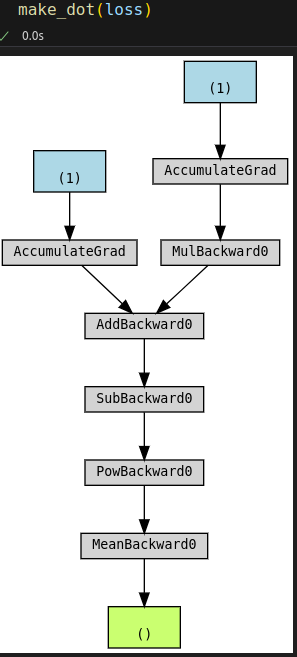
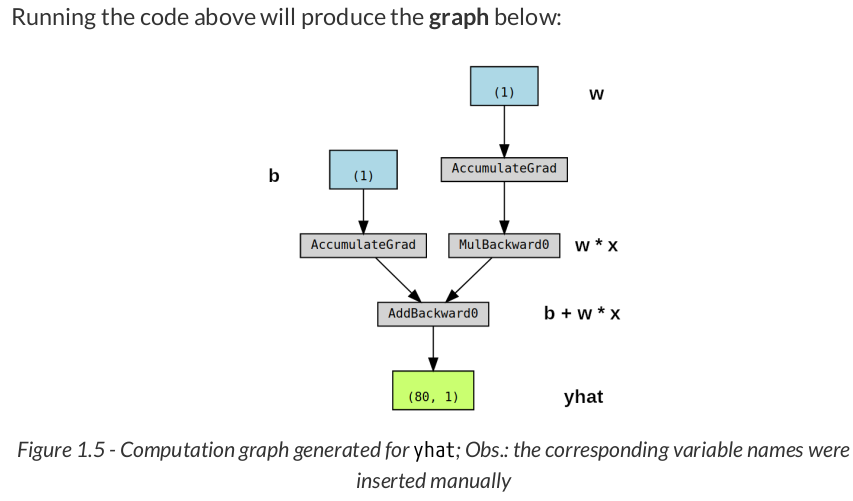
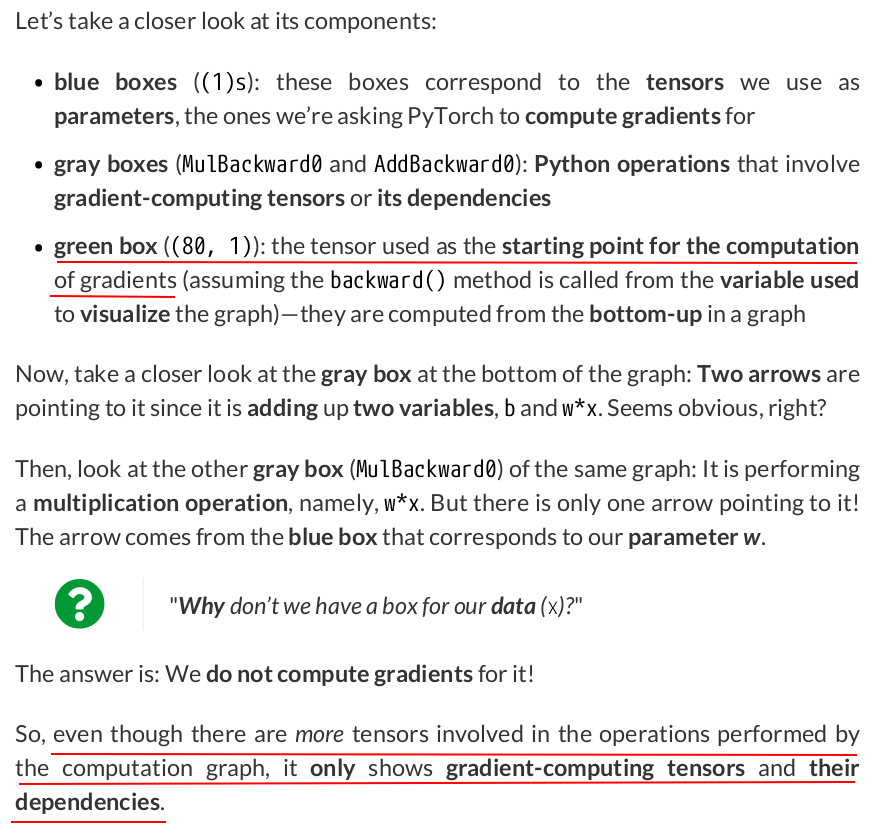
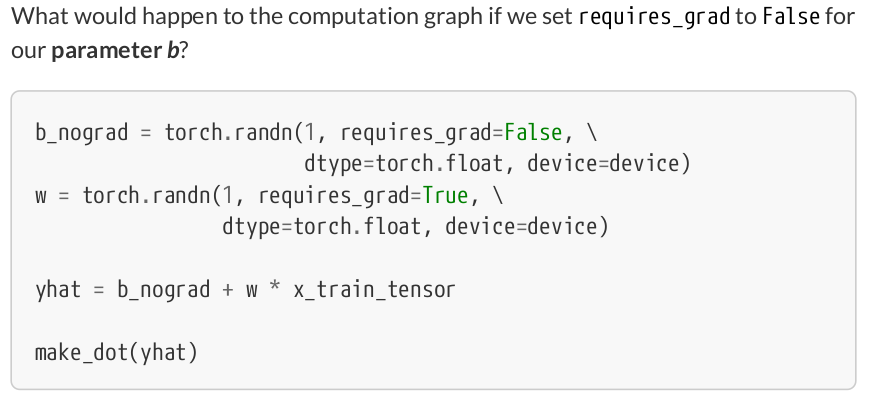


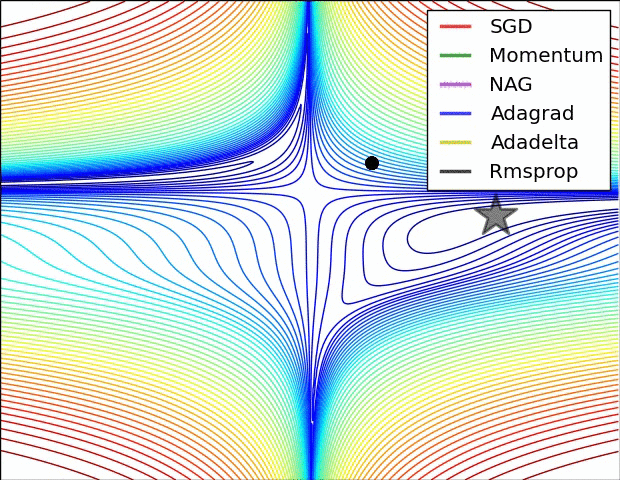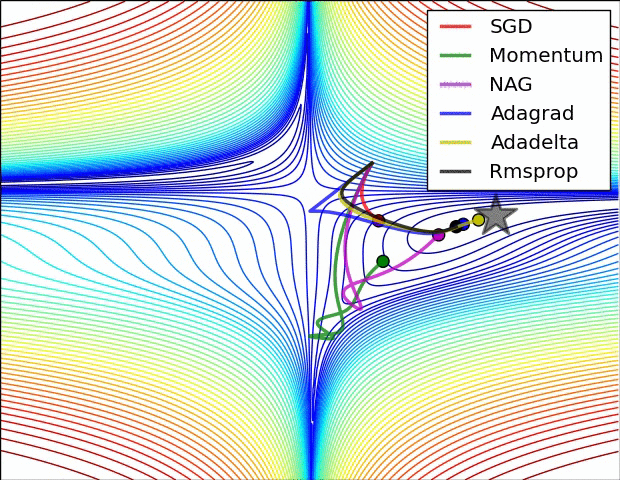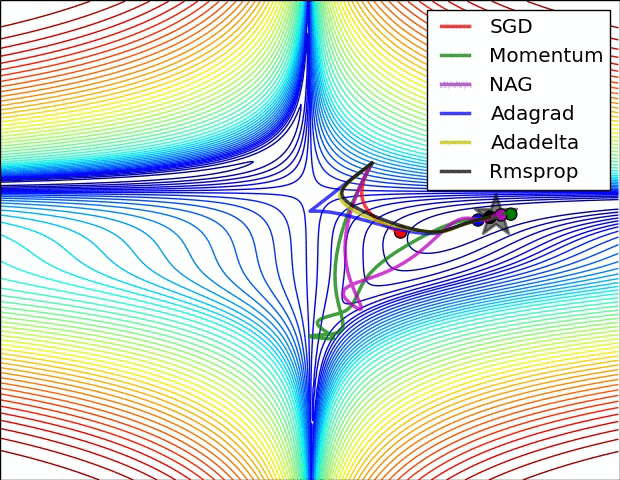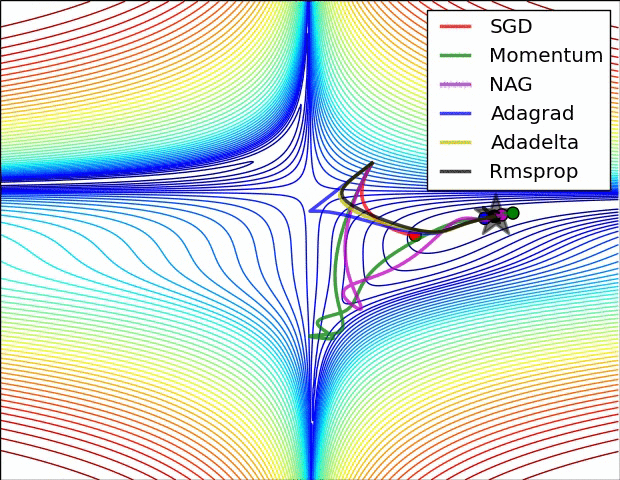

# Define a SGD optimizer to update the parameters optimizer = torch.optim.SGD([b, w], lr=lr)

# Set learning rate - this is eta lr = 0.1 # Step 0 - Initialize parameters "b" and "w" randomly torch.manual_seed(42) b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) w = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) # Define a SGD optimizer to update the parameters optimizer = torch.optim.SGD([b, w], lr=lr) # Define number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train_tensor # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. error = yhat - y_train_tensor loss = (error ** 2).mean() # MSE # Step 3 - Compute gradients for both "b" and "w" parameters loss.backward() # Step 4 - Update parameters using gradients and the learning rate # with torch.no_grad(): # b -= lr * b.grad # w -= lr * w.grad optimizer.step() # No more telling Pytorch to let gradients go! # b.grad.zero_() # w.grad.zero_() optimizer.zero_grad() print(b) # tensor([0.9719], device='cuda:0', requires_grad=True) print(w) # tensor([2.0522], device='cuda:0', requires_grad=True)

# Define a MSE loss function loss_fn = torch.nn.MSELoss(reduction='mean') # nn stands for neural network # This is a random example to illustrate the loss function predictions = torch.tensor([0.5, 1.0]) labels = torch.tensor([2.0, 1.3]) loss_fn(predictions, labels) # tensor(1.1700)


# Set learning rate - this is eta lr = 0.1 # Step 0 - Initialize parameters "b" and "w" randomly torch.manual_seed(42) b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) w = torch.randn(1, requires_grad=True, dtype=torch.float, device=device) # Define a SGD optimizer to update the parameters optimizer = torch.optim.SGD([b, w], lr=lr) # Define a MSE loss function loss_fn = torch.nn.MSELoss(reduction='mean') # Define number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Step 1 - Compute model's predictions - forward pass yhat = b + w * x_train_tensor # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. loss = loss_fn(yhat, y_train_tensor) # Step 3 - Compute gradients for both "b" and "w" parameters loss.backward() # Step 4 - Update parameters using gradients and the learning rate optimizer.step() optimizer.zero_grad() print(b) # tensor([0.9719], device='cuda:0', requires_grad=True) print(w) # tensor([2.0522], device='cuda:0', requires_grad=True)

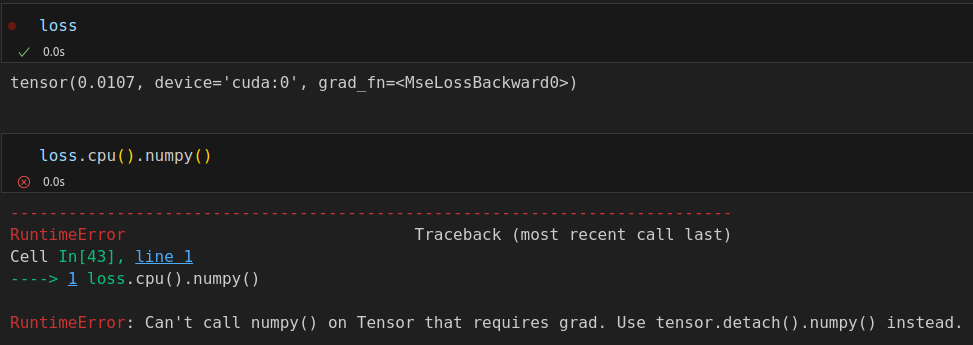

loss.detach().cpu().numpy() # array(0.0106975, dtype=float32) print(loss.item()) # 0.010697497986257076 print(loss.tolist()) # 0.010697497986257076



class ManualLinearRegression(nn.Module): def __init__(self): super().__init__() # To make "b" and "w" real parameters of the model, we need to wrap them with nn.Parameter self.b = nn.Parameter(torch.randn(1, requires_grad=True, dtype=torch.float, device=device)) self.w = nn.Parameter(torch.randn(1, requires_grad=True, dtype=torch.float, device=device)) def forward(self, x): # Compute the predictions return self.b + self.w * x

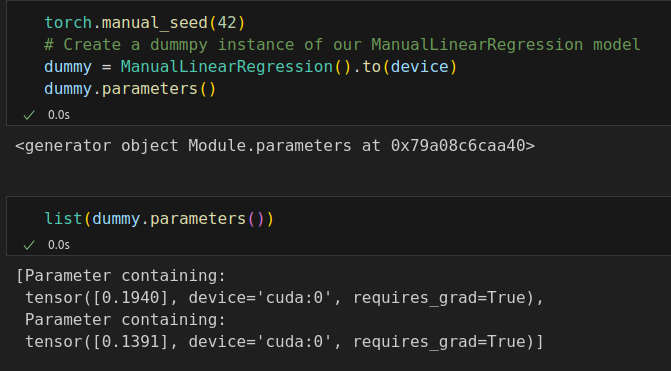

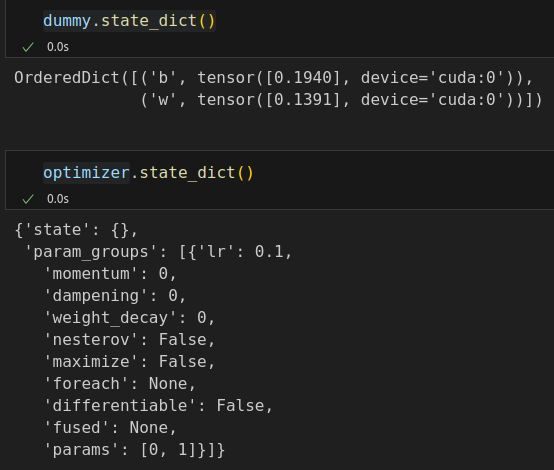
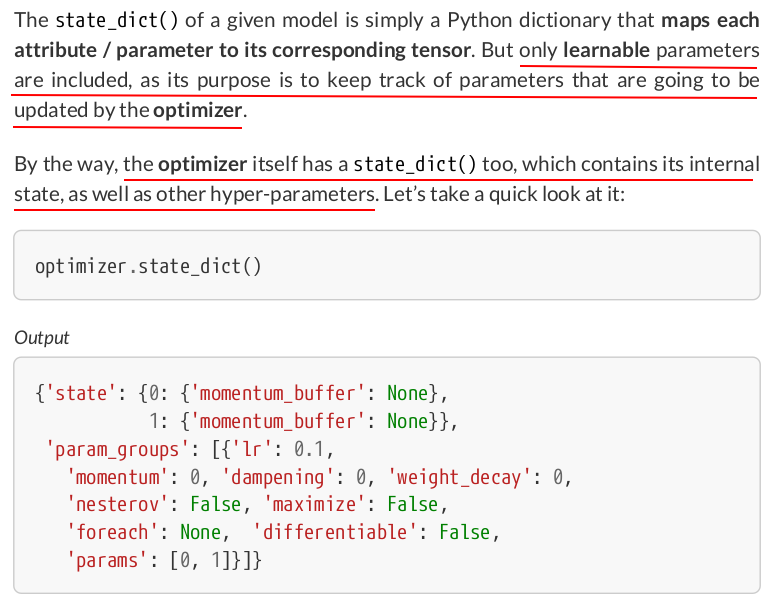


# Set learning rate - this is eta lr = 0.1 # Step 0 - Initialize parameters "b" and "w" randomly torch.manual_seed(42) model = ManualLinearRegression().to(device) # Define a SGD optimizer to update the parameters # (now retrieved directly from the model) optimizer = torch.optim.SGD(model.parameters(), lr=lr) # Define a MSE loss function loss_fn = nn.MSELoss(reduction='mean') # Define number of epochs n_epochs = 1000 for epoch in range(n_epochs): model.train() # What is this? # Step 1 - Compute model's predictions - forward pass # No more manual prediction! yhat = model(x_train_tensor) # Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. loss = loss_fn(yhat, y_train_tensor) # Step 3 - Compute gradients for both "b" and "w" parameters loss.backward() # Step 4 - Update parameters using gradients and the learning rate optimizer.step() optimizer.zero_grad() # We can also inspect its parameters using its state_dict print(model.state_dict()) # OrderedDict({'b': tensor([1.0028], device='cuda:0'), 'w': tensor([2.0090], device='cuda:0')})

linear = nn.Linear(1, 1).to(device) linear.state_dict() # OrderedDict([('weight', tensor([[-0.2191]], device='cuda:0')), # ('bias', tensor([0.2018], device='cuda:0'))])



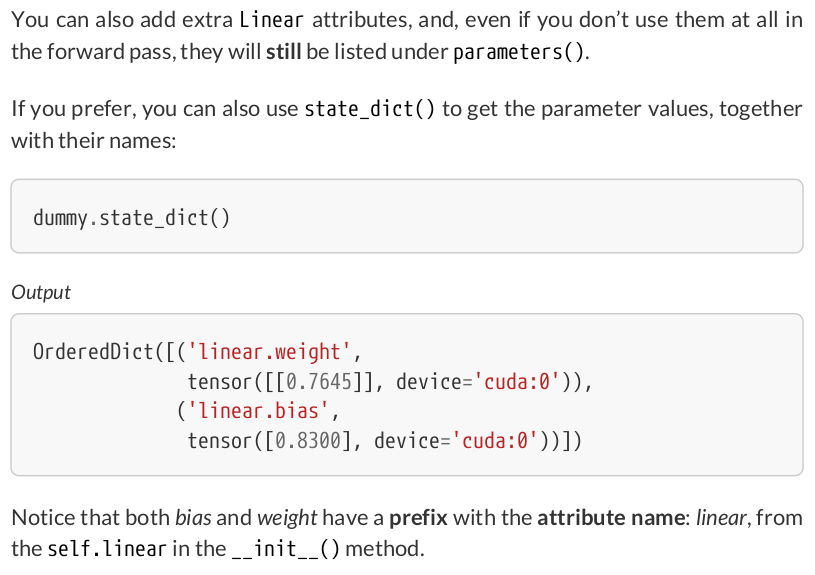

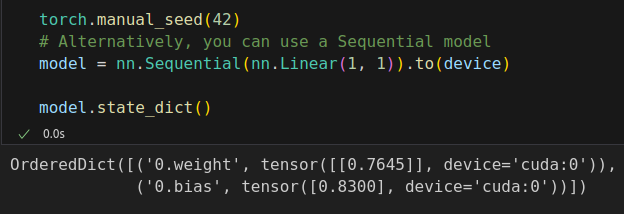

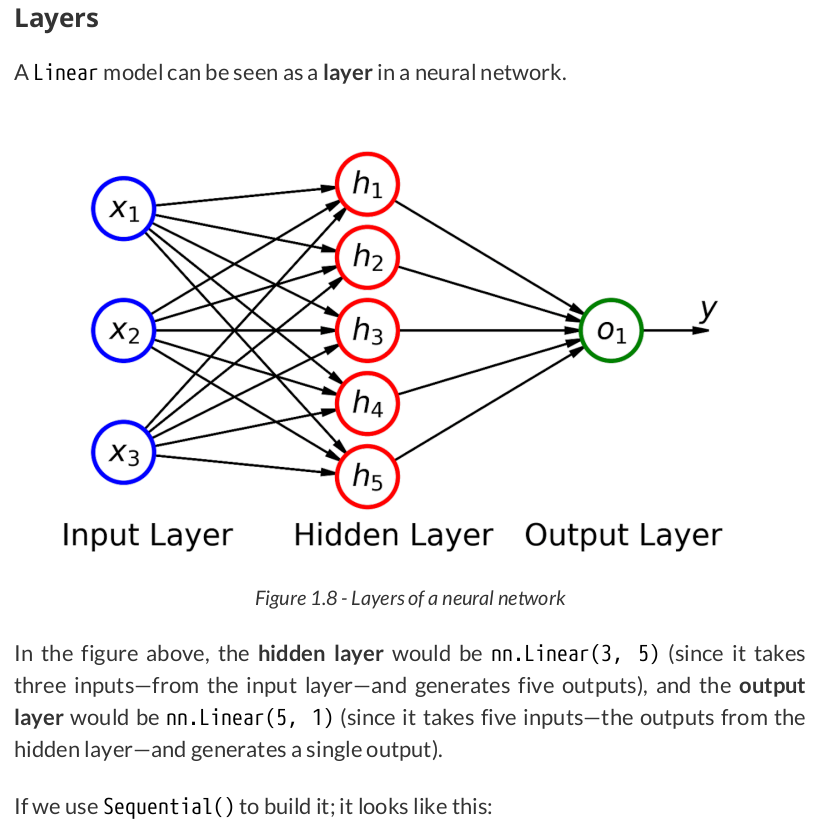
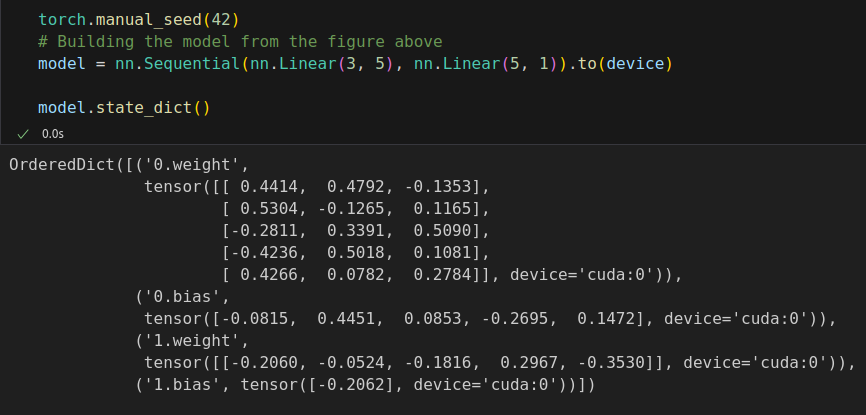

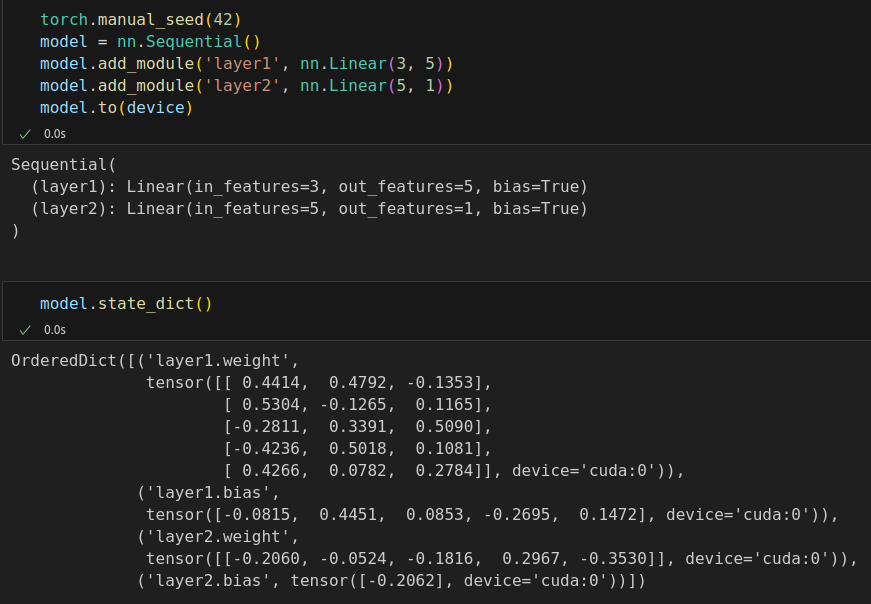


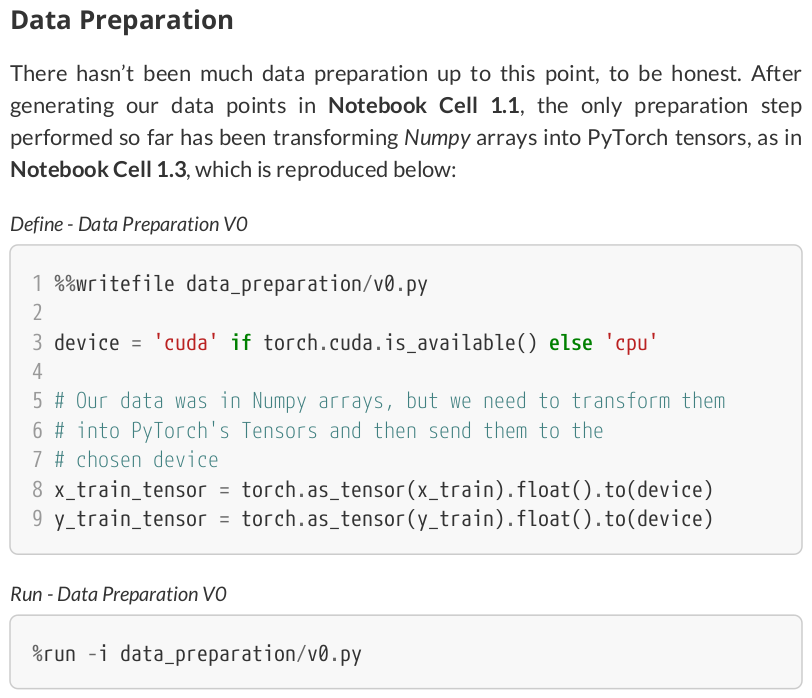




%%writefile model_configuration/v0.py # This is redundant now, but it won't be when we introduce Datasets... device = 'cuda' if torch.cuda.is_available() else 'cpu' # Set learning rate - this is eta lr = 0.1 torch.manual_seed(42) # Now we can create a model and send it at once to the device model = nn.Sequential(nn.Linear(1, 1)).to(device) # Define a SGD optimizer to update the parameters # (now retrieved directly from the model) optimizer = torch.optim.SGD(model.parameters(), lr=lr) # Define a MSE loss function loss_fn = nn.MSELoss(reduction='mean')
%run -i model_configuration/v0.py




%%writefile model_training/v0.py # Define number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Set model to TRAIN mode model.train() # Step 1 - Compute model's predictions - forward pass yhat = model(x_train_tensor) # Step 2 - Compute the loss loss = loss_fn(yhat, y_train_tensor) # Step 3 - Compute gradients for both "b" and "w" parameters loss.backward() # Step 4 - Update parameters using gradients and the learning rate optimizer.step() optimizer.zero_grad()
%run -i model_training/v0.py
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
File /zdata/Github/pytorchsbs/model_training/v0.py:10
7 model.train()
9 # Step 1 - Compute model's predictions - forward pass
---> 10 yhat = model(x_train_tensor)
12 # Step 2 - Compute the loss
13 loss = loss_fn(yhat, y_train_tensor)
File /zdata/Github/zpytorch/lib/python3.12/site-packages/torch/nn/modules/module.py:1553, in Module._wrapped_call_impl(self, *args, **kwargs)
1551 return self._compiled_call_impl(*args, **kwargs) # type: ignore[misc]
1552 else:
-> 1553 return self._call_impl(*args, **kwargs)
File /zdata/Github/zpytorch/lib/python3.12/site-packages/torch/nn/modules/module.py:1562, in Module._call_impl(self, *args, **kwargs)
1557 # If we don't have any hooks, we want to skip the rest of the logic in
1558 # this function, and just call forward.
1559 if not (self._backward_hooks or self._backward_pre_hooks or self._forward_hooks or self._forward_pre_hooks
1560 or _global_backward_pre_hooks or _global_backward_hooks
1561 or _global_forward_hooks or _global_forward_pre_hooks):
-> 1562 return forward_call(*args, **kwargs)
1564 try:
1565 result = None
File /zdata/Github/zpytorch/lib/python3.12/site-packages/torch/nn/modules/container.py:219, in Sequential.forward(self, input)
...
File /zdata/Github/zpytorch/lib/python3.12/site-packages/torch/nn/modules/linear.py:117, in Linear.forward(self, input)
116 def forward(self, input: Tensor) -> Tensor:
--> 117 return F.linear(input, self.weight, self.bias)
RuntimeError: mat1 and mat2 shapes cannot be multiplied (1x80 and 1x1)
To fix the error, reshape x_train_tensor:
%%writefile model_training/v0.py # Define number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Set model to TRAIN mode model.train() # Step 1 - Compute model's predictions - forward pass yhat = model(x_train_tensor.reshape(-1, 1)) # Step 2 - Compute the loss loss = loss_fn(yhat, y_train_tensor) # Step 3 - Compute gradients for both "b" and "w" parameters loss.backward() # Step 4 - Update parameters using gradients and the learning rate optimizer.step() optimizer.zero_grad()
Got a warning:
UserWarning: Using a target size (torch.Size([80])) that is different to the input size (torch.Size([80, 1])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
return F.mse_loss(input, target, reduction=self.reduction)
To fix the warning, reshape y_train_tensor too:
%%writefile model_training/v0.py # Define number of epochs n_epochs = 1000 for epoch in range(n_epochs): # Set model to TRAIN mode model.train() # Step 1 - Compute model's predictions - forward pass yhat = model(x_train_tensor.reshape(-1, 1)) # Step 2 - Compute the loss loss = loss_fn(yhat, y_train_tensor.reshape(-1, 1)) # Step 3 - Compute gradients for both "b" and "w" parameters loss.backward() # Step 4 - Update parameters using gradients and the learning rate optimizer.step() optimizer.zero_grad()









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律