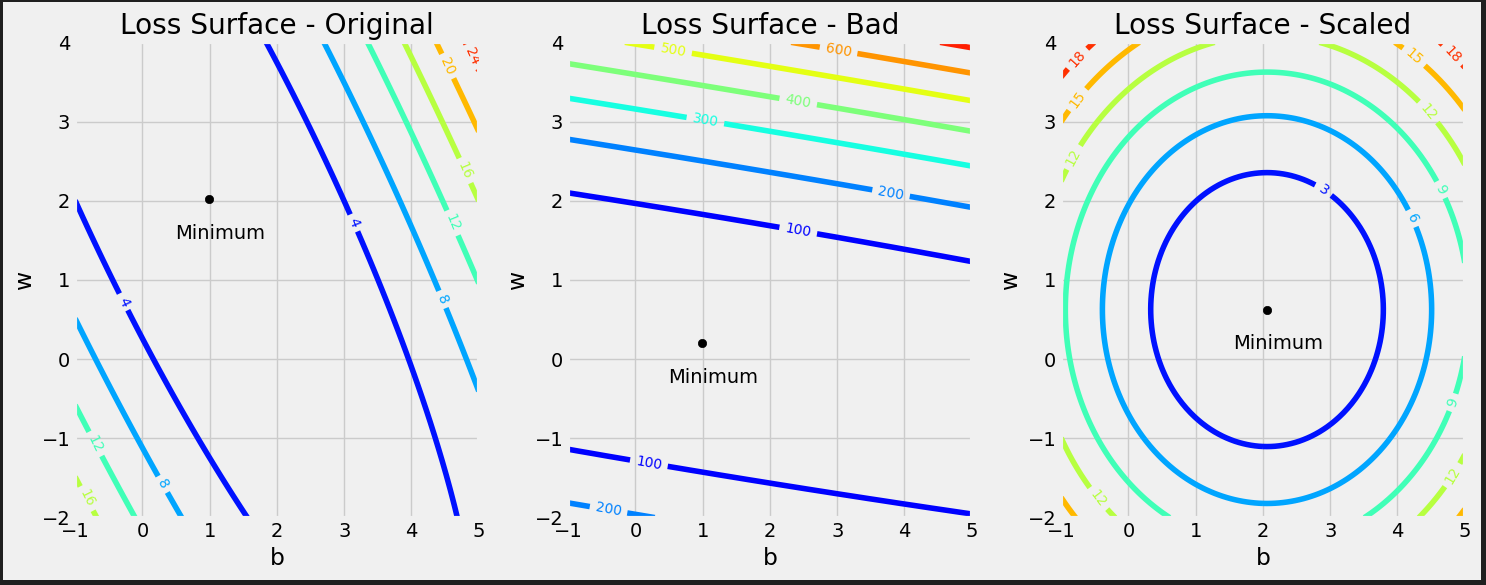
Gradient descent is an iterative technique commonly used in machine learning and deep learning to find the best possible set of parameters / coefficients for a given model, data points, and loss function, starting from an initial, and usually random, guess.




import numpy as np true_b = 1 true_w = 2 N = 100 # Data Generationrng = np.random.default_rng(54321) x = rng.random(N) epsilon = (0.1 * rng.standard_normal(N)) y = true_b + true_w * x + epsilon
print(x.shape) print(y.shape)
(100,)
(100,)



# Shuffle the indices idx = np.arange(N) np.random.shuffle(idx) # Use first 80 random indices for train train_idx = idx[:int(N * 0.8)] # Use the ramaining indices for validation val_idx = idx[int(N * 0.8):] # Generate train and validation sets x_train, y_train = x[train_idx], y[train_idx] x_val, y_val = x[val_idx], y[val_idx]



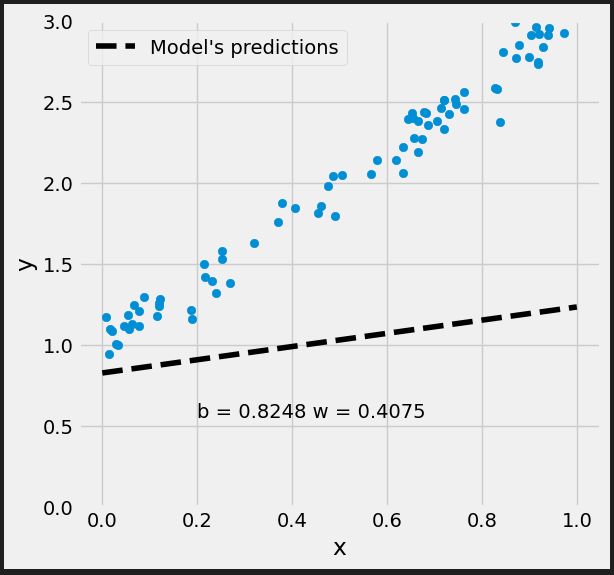
# Step 0 - Initialize parameters "b" and "w" randomly rng = np.random.default_rng(54321) b = rng.standard_normal(1) w = rng.standard_normal(1) print(b, w) # [0.82483768] [0.40749068]

# Step 1 - Compute our model's predicted output - forward pass yhat = b + w * x_train

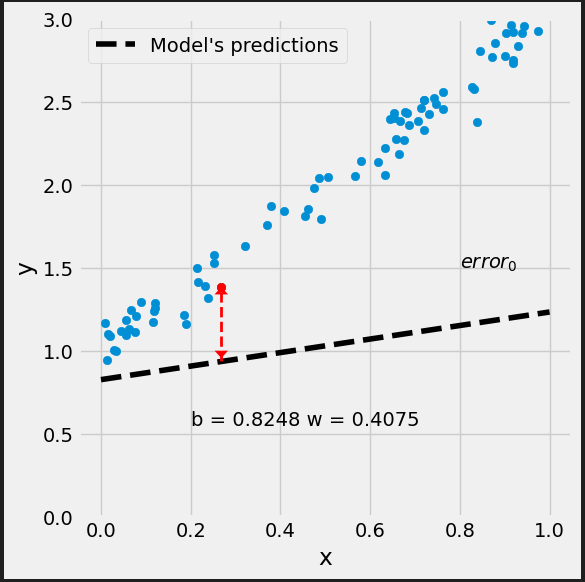



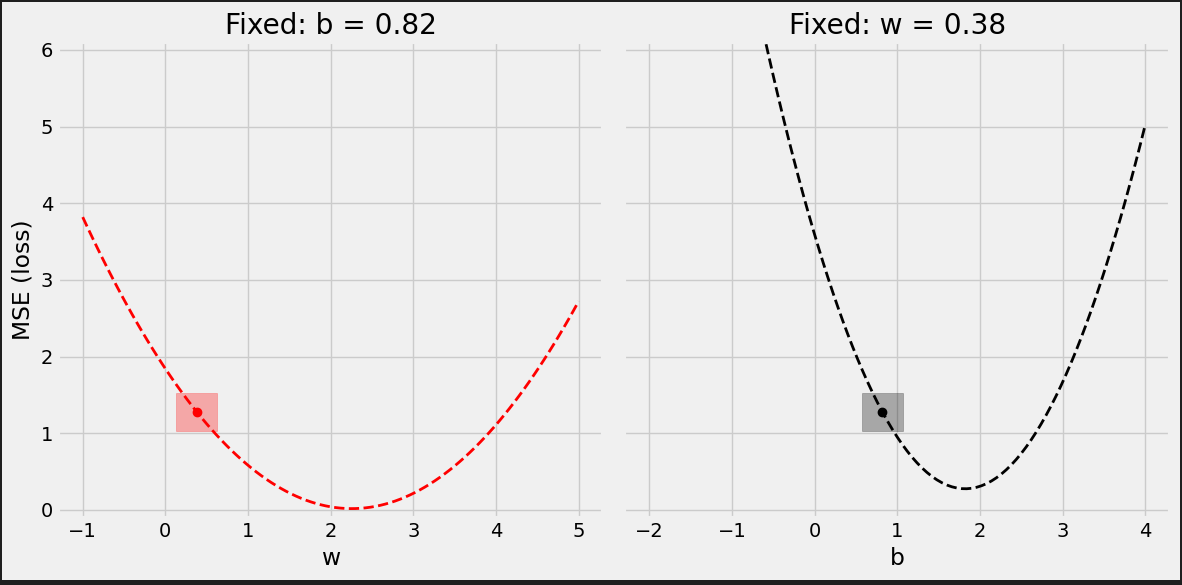
# Step 2 - Compute the loss # We are using ALL data points, so this is BATCH gradient descent. # How wrong is our model? That's the error! error = yhat - y_train # It is a regression, so it computes mean squared error (MSE) loss = (error ** 2).mean()

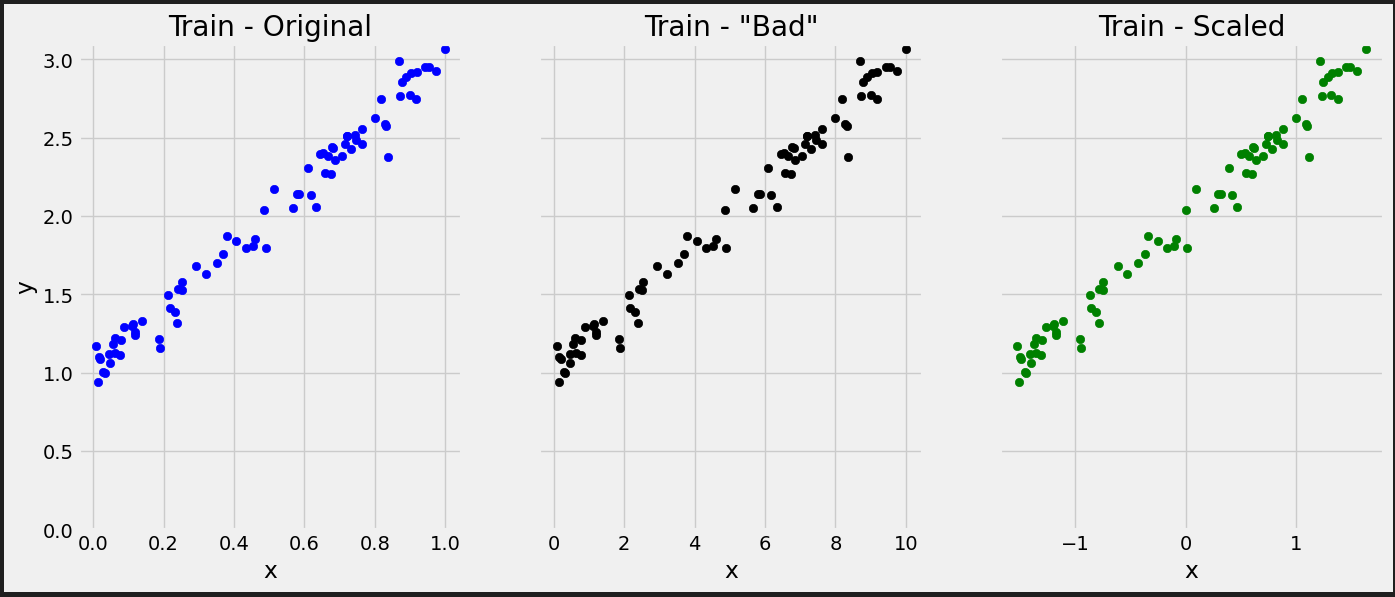
# Reminder: # true_b = 1 # true_w = 2 # We have to split the ranges in 100 evenly spaced intervals each. # Sure, we’re somewhat cheating here, since we know the true values of b and w, so we can # choose the perfect ranges for the parameters. But it is for educational purposes only. b_range = np.linspace(true_b - 3, true_b + 3, 101) w_range = np.linspace(true_w - 3, true_w + 3, 101) # meshgrid is a handy function that generates a grid of b and w values for all combinations bs, ws = np.meshgrid(b_range, w_range) bs.shape, ws.shape # ((101, 101), (101, 101))
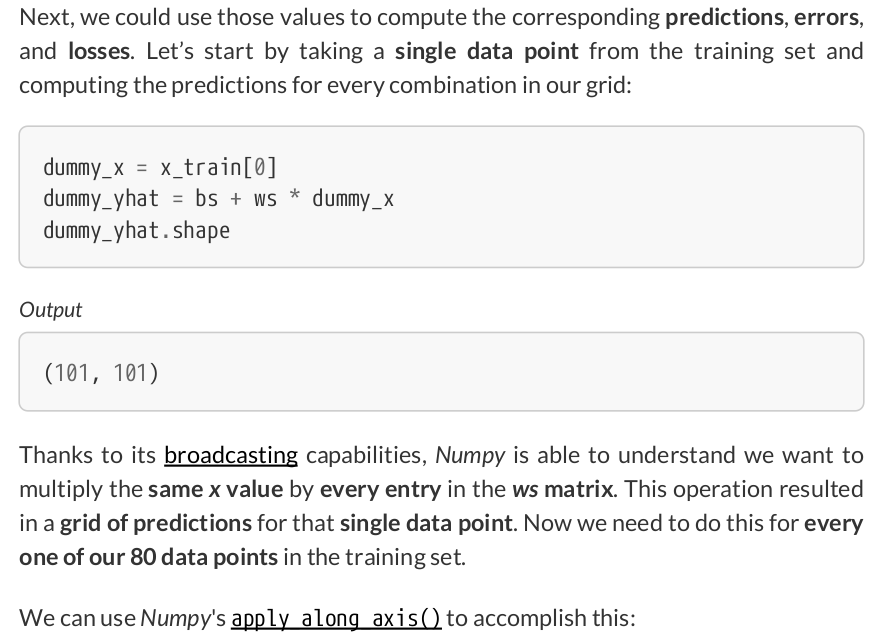
print(x_train.reshape(-1, 1).shape) # (80, 1)
all_predictions = np.apply_along_axis( func1d=lambda x: bs + ws * x, axis=1, arr=x_train.reshape(-1, 1), ) all_predictions.shape # (80, 101, 101)

all_labels = y_train.reshape(-1, 1, 1) all_labels.shape # (80, 1, 1)

all_errors = all_predictions - all_labels all_errors.shape # (80, 101, 101)
Each prediction has its own error, so we get 80 matrices of shape (101, 101), again, one matrix for each data point, each matrix containing a grid of errors.

all_losses = (all_errors ** 2).mean(axis=0) all_losses.shape # (101, 101)

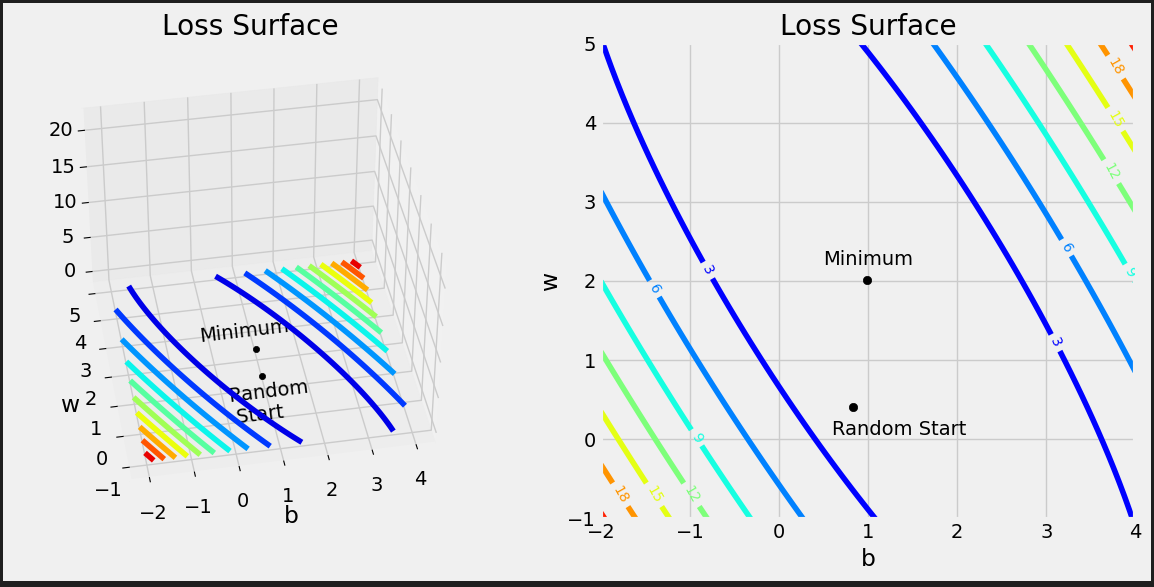





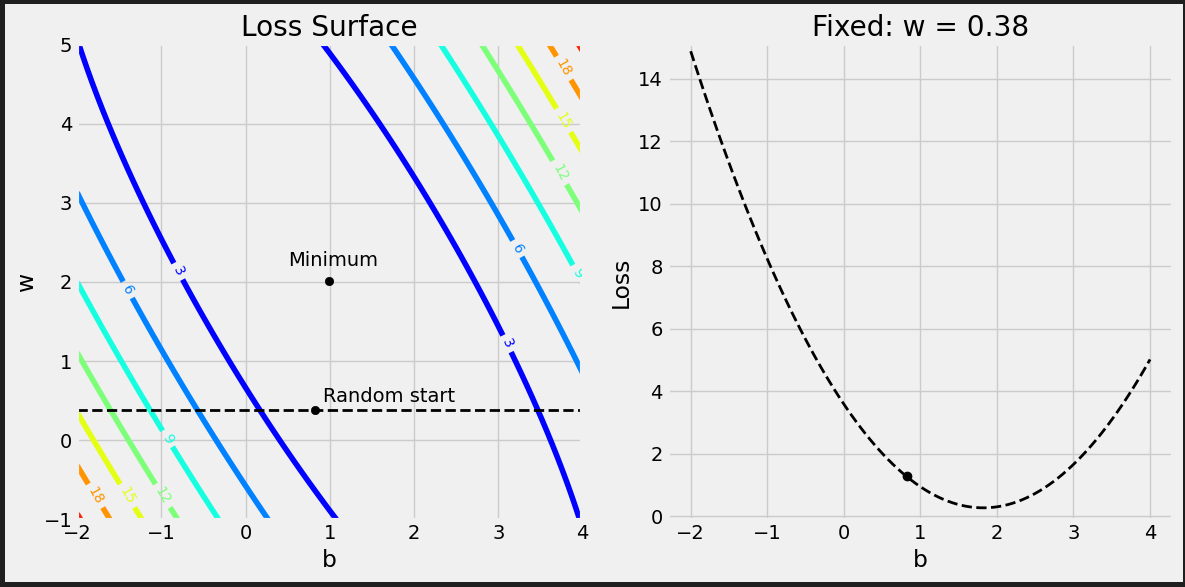




# Step 3 - Compute gradients for both "b" and "w" parameters b_grad = 2 * error.mean() w_grad = 2 * (x_train * error).mean() print(b_grad, w_grad) # -1.965279236007916 -1.3213968667849743



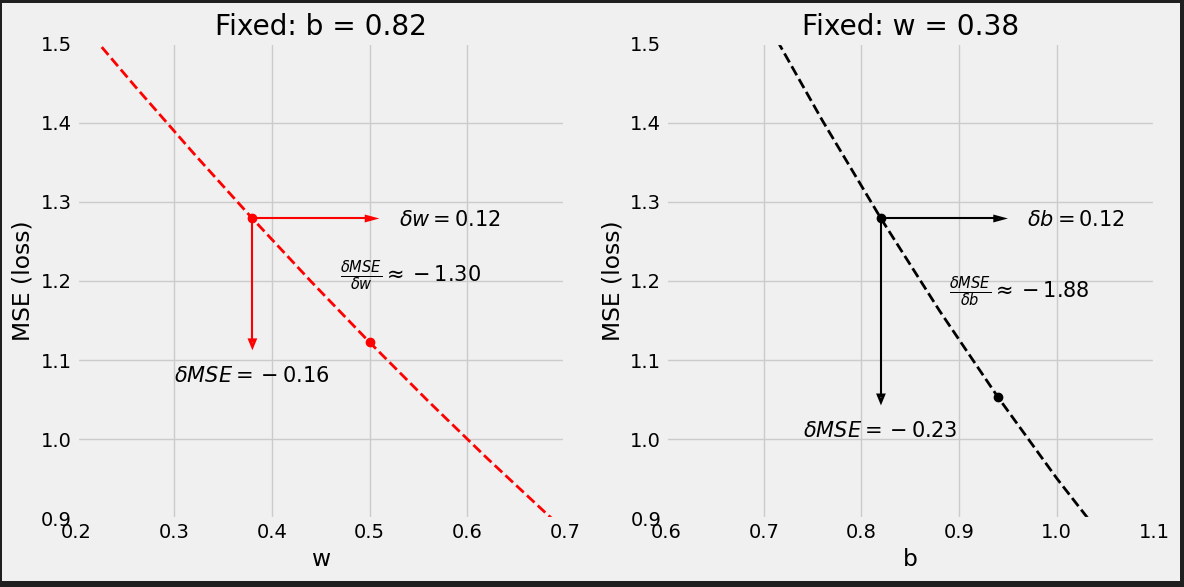





以gradients作为learning rate的权重来更新parameters.

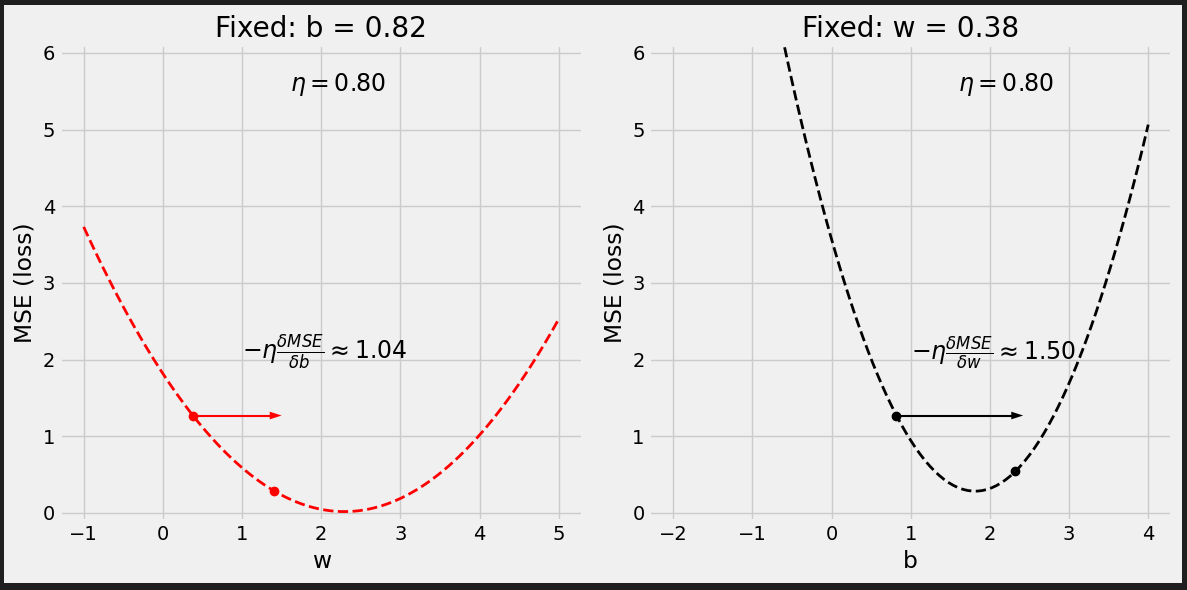
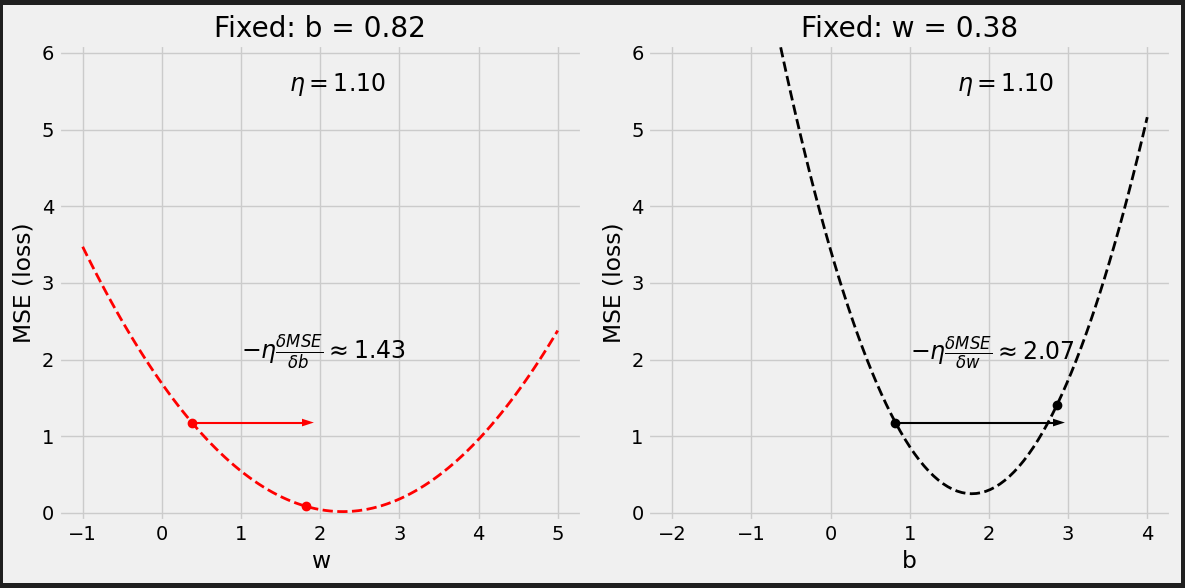
# Set learning rate - this is "eta" lr = .1 print(b, w) # [0.82483768] [0.40749068] # Step 4 - Update parameters using gradients and the learning rate b = b - lr * b_grad w = w - lr * w_grad print(b, w) # [1.02136561] [0.53963036]

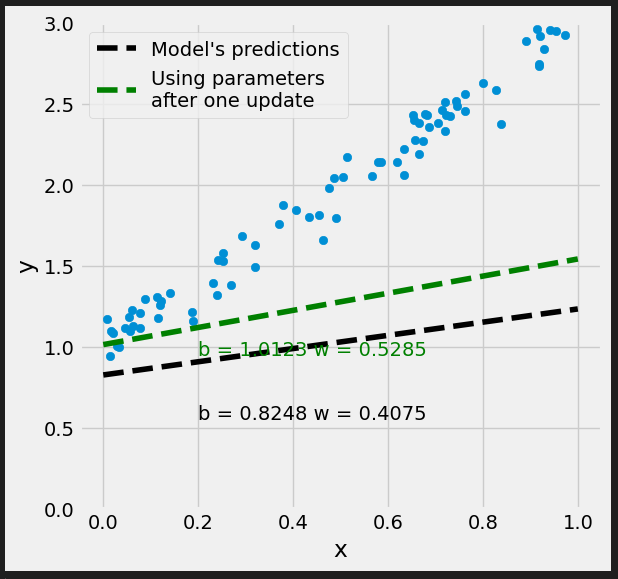
Figure 0.9 - Updated model’s predictions
It looks better.












true_b = 1 true_w = 2 N = 100 # Data Generation rng = np.random.default_rng(54321) # We divide w by 10 bad_w = true_w / 10 # And multiply x by 10 bad_x = rng.random(N) * 10 epsilon = 0.1 * rng.standard_normal(N) # So, the net effect on y is zero - it is still the same as before y = true_b + bad_w * bad_x + epsilon

# Generate train and validation sets # Use the same train_idx and val_idx as before, but apply to bad_x bad_x_train, y_train = bad_x[train_idx], y[train_idx] bad_x_val, y_val = bad_x[val_idx], y[val_idx]
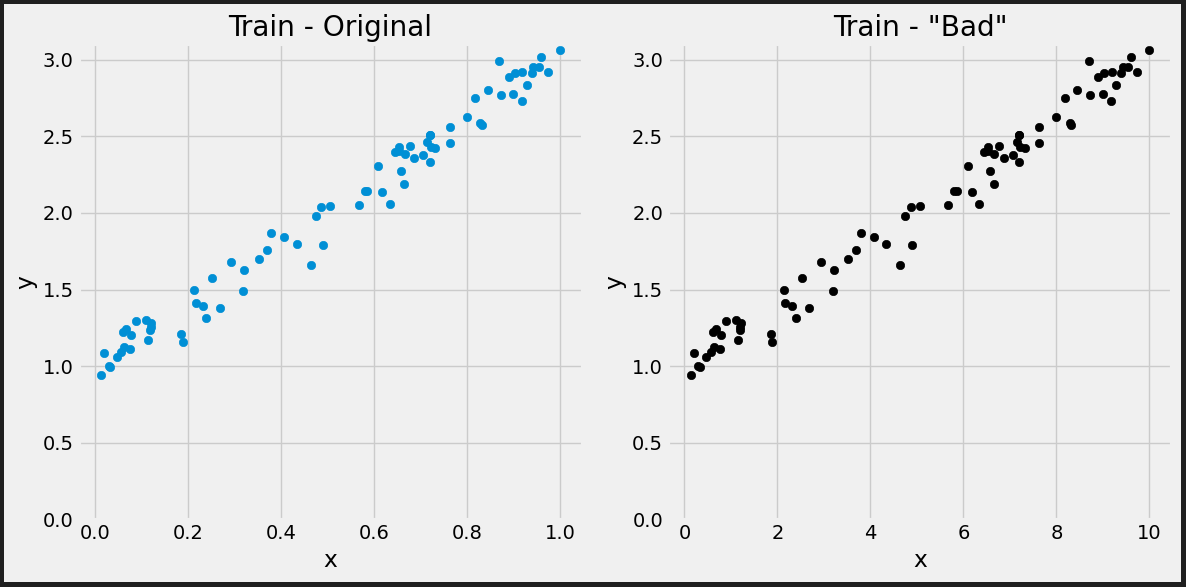
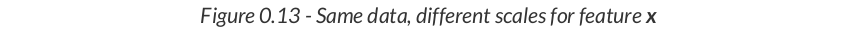

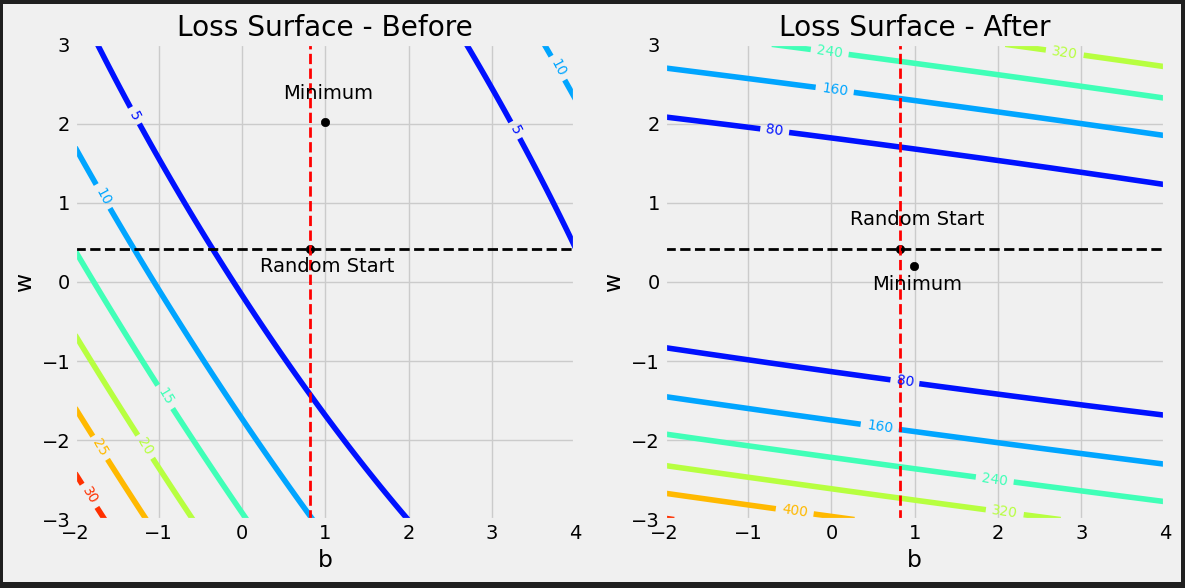







from sklearn.preprocessing import StandardScaler scaler = StandardScaler(with_mean=True, with_std=True) # We use the TRAIN set ONLY to fit the scaler scaler.fit(x_train.reshape(-1, 1)) # Now we can use the already fit scaler to TRANSFORM both TRAIN and VALIDATION sets scaled_x_train = scaler.transform(x_train.reshape(-1, 1)) scaled_x_val = scaler.transform(x_val.reshape(-1, 1))

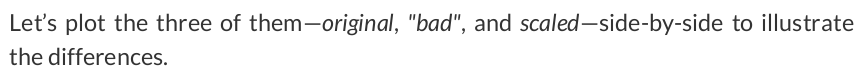


















【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律