Finite state machines (FSMs) serve as a great example of an important theoretical construction that also turns out to be a useful tool for everyday programming. In its basic form, an FSM performs only one kind of job: it processes an input string of symbols and decides whether it should be accepted or rejected. A sketch of this virtual device is shown in Figure 7.1.
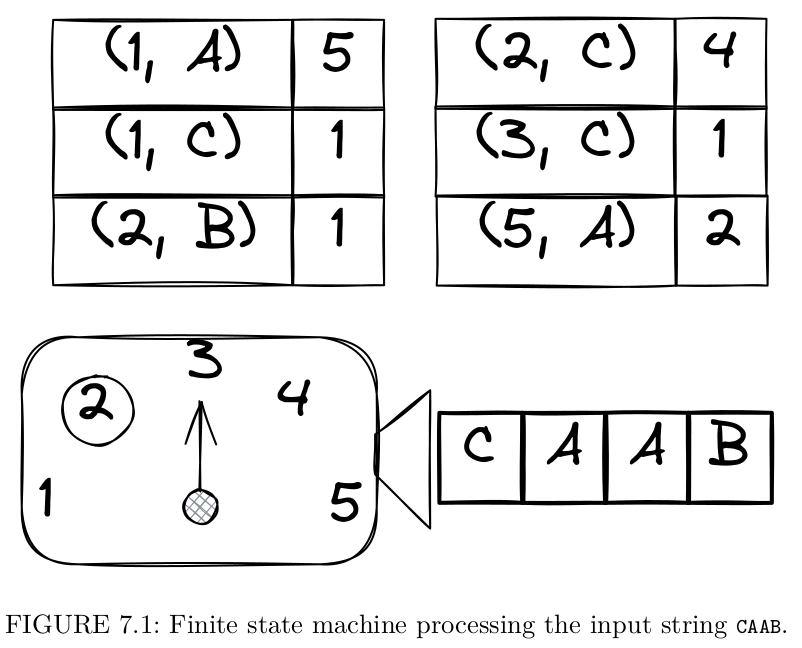
An FSM always resides in a certain state (pointed by the needle in the sketch). One of them is chosen as the initial state. One or more states are also chosen as “favorable”. The machine shown in the figure starts its work in state 3, and its only favorable state is 2.
The machine operates according to the transition rules, specifying the target state for each possible combination of the current state and the next input symbol. Thus, the machine reads the input string symbol-by-symbol and switches between the states. If, after reading the whole input, it happens to be in one of the favorable states, the string is accepted.
Instead of actually writing down a rule for every combination of state and symbol, it is usually presumed that unexpected situations cause the input string to be rejected. For example, in our case there is no rule for the combination (3, A). Thus, any input string starting with A is going to be rejected.
Let’s see what happens during processing of the example string CAAB:
1. Machine reads C and switches to 1 using rule (3, C) → 1.
2. Machine reads A and switches to 5 using rule (1, A) → 5.
3. Machine reads A and switches to 2 using rule (5, A) → 2.
4. Machine reads B and switches to 1 using rule (2, B) → 1.
The final state is not favorable, and the input string is therefore rejected.
Each FSM accepts certain strings and rejects other strings. Our device will accept a variety of strings, including, for instance, CCAA, CCCAA, and CCAABAA. Thus, an FSM divides all possible strings in the world into two classes: the strings it accepts and the strings it rejects.1 Unsurprisingly, FSMs are often used in practice specifically for this purpose: to figure out whether an input string belongs to a class of our interest or not. For example, it is possible to construct a device that would only accept strings forming a time description in a 24-hour format (such as 12:35 or 00:15) or a valid Python variable name.
Some classes of strings, however, turn out to be an unreachable target for FSMs. Say, it is impossible to construct an FSM that would accept any string that reads the same both ways (a palindrome), such as “kayak” or “racecar”. Intuitively, it is not hard to see why: an FSM has states, but no writable memory, so it cannot keep track of incoming symbols to check whether the same symbols reappear in the reverse order later.
This observation is an important result in theoretical computer science, where distinction is made between the sets of strings that can be recognized by an FSM, and the sets of strings requiring more powerful computational devices. Thus, FSMs mark a certain threshold of computational capacity. Note that “strings of symbols” do not necessarily mean “strings of characters”: FSMs process sequences of arbitrary elements, which makes them useful far beyond the tasks of text processing. Before we move on, let me add that FSMs are typically visualized with diagrams, depicting their states and transitions between them.
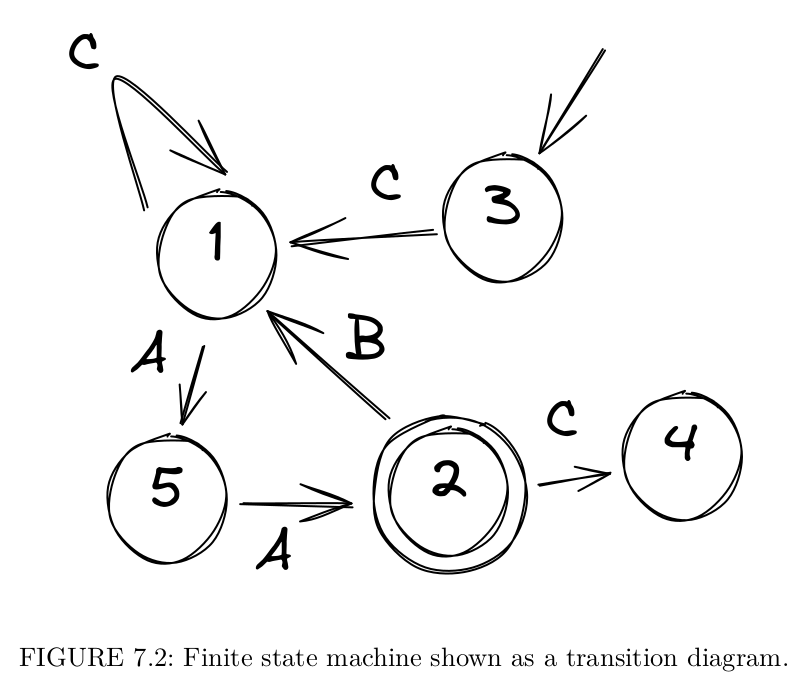
TIME MACHINE
The goal of our next little exercise is to create an FSM actually doing something useful. As mentioned in the previous section, it is possible to design an FSM that accepts strings forming time descriptions such as 12:35. Imagine an input box where the user has to supply a time value. The program must make sure the value is valid before using it.
Let’s create such a device. To make things a bit more interesting, let’s presume the time format is HH:MM[:SS[.fff]]
There are two digits for hours, two digits for minutes, an optional two-digit part for seconds, and in case it is present, an additional optional part for milliseconds (ranging from 000 to 999). Thus, these are valid time strings:00:30, 13:45:59, 23:03:15.003.
This particular data format is quite simple, so the corresponding FSM can be drawn without much preparation (see Figure 7.3).
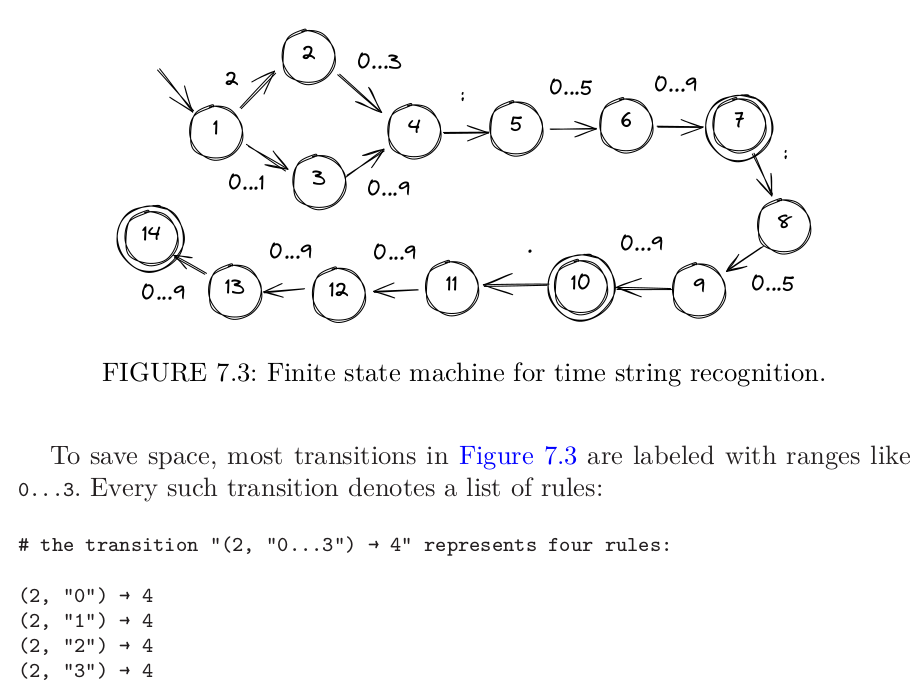
A valid string starts with a digit 0, 1, or 2. Since the highest value for hours is 23, the digit after 2 must be no larger than 3. Then we expect a colon and a minutes chunk, which is a digit in a range 0-5 followed by a digit in a range 0-9. Since a valid string may end here, state 7 is favorable. Seconds work in the same way as minutes, and there is yet another favorable state after their chunk. The trailing part of the string, milliseconds, consists of a dot and three digits.
def accept(rules, favorable_states, start, input): state = start try: for c in input: state = rules[(state, c)] return state in favorable_states except KeyError: return False def rules_range(state_from, state_to, min_char, max_char): r = range(ord(min_char), ord(max_char) + 1) return {(state_from, chr(u)): state_to for u in r} # hours rules = {(1, "2"): 2} rules.update(rules_range(1, 3, "0", "1")) rules.update(rules_range(2, 4, "0", "3")) rules.update(rules_range(3, 4, "0", "9")) # colon rules.update({(4, ":"): 5}) # minutes rules.update(rules_range(5, 6, "0", "5")) rules.update(rules_range(6, 7, "0", "9")) # colon rules.update({(7, ":"): 8}) # seconds rules.update(rules_range(8, 9, "0", "5")) rules.update(rules_range(9, 10, "0", "9")) # dot rules.update({(10, "."): 11}) # milliseconds rules.update(rules_range(11, 12, "0", "9")) rules.update(rules_range(12, 13, "0", "9")) rules.update(rules_range(13, 14, "0", "9")) start = 1 favorable_states = {7, 10, 14} print(accept(rules, favorable_states, start, "23:15")) # True print(accept(rules, favorable_states, start, "24:15")) # False print(accept(rules, favorable_states, start, "09:37")) # True print(accept(rules, favorable_states, start, "23:95")) # False print(accept(rules, favorable_states, start, "00:15:23")) # True print(accept(rules, favorable_states, start, "05:23:59.234")) # True
An FSM can be used to describe the changes of a certain system over time if these changes are deterministic.
