Lindenmayer systems (or L-systems)

Among the most conspicuous properties of a plant shape are symmetry and self-similarity.

 

In a nutshell, L-systems are based on three foundational ideas. The first idea is to represent plant structure with a string of characters. For example, suppose that a certain type of a plant is made of three kinds of elements: a trunk element I, a left leaf L, and a right leaf R. A little specimen of this plant, consisting of a single trunk element and two leaves, can be described with a string LRI (see Figure 5.5).

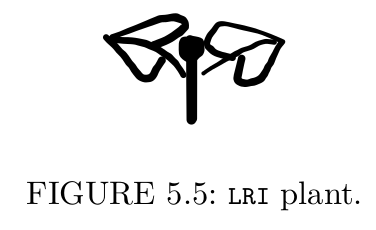
Note that any particular image is just an illustration of one of many possible looks of the LRI plant. The textual description does not really dictate any particular appearance, it is only responsible for the internal structure of the entity we describe.

 

Having enough patience, one can create fairly complicated plants using this approach, but in practice the description strings quickly become long and difficult to work with. Thus, the second foundational idea is to specify the developmental rules of the plant in the form predecessor → successor

We can make our LRI plant growable by introducing a new element A (“root”) and specifying its developmental rule:
A → ALRI

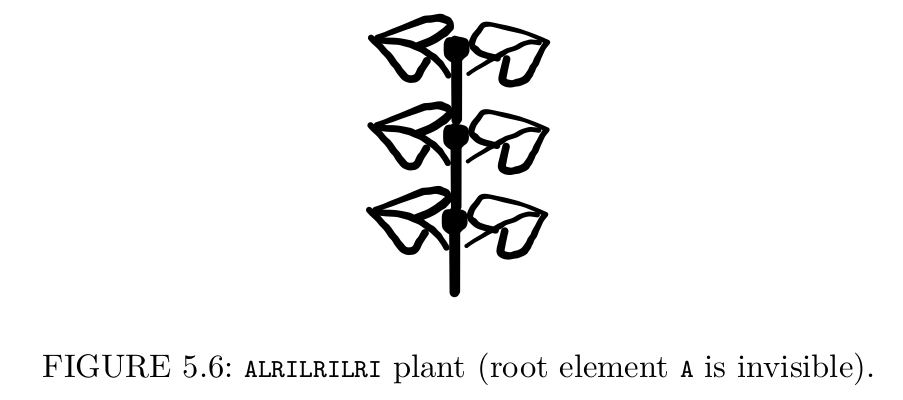
Now let’s “seed” the initial plant, consisting only of the root element A. After three applications of the developmental rule, we will obtain a “triple-LRI” plant (see Figure 5.6):
A → ALRI → ALRILRI → ALRILRILRI

 

Summing up, an L-system is a description of a plant structure, consisting of an initial string (called an axiom) and a set of production rules that determine how individual symbols “grow” into strings. On each “growth step” all the symbols of the current string are substituted according to the rules. It is also presumed that no rules are in conflict, so if we have a rule A → B, there should be no alternative rule A → C.

 

As a more complex example, consider the evolution of the axiom g according to the production rule g → g[+g][-g]:

step 0: g
step 1: g[+g][-g]
step 2: g[+g][-g][+g[+g][-g]][-g[+g][-g]]

This way, every occurrence of g in the current string becomes g[+g][-g] at the next step. This process can go on forever, but in practice it is usually interesting to watch the evolution of a certain axiom over the predefined number of generations or simply visualize the final result.

 

The third and the final foundational idea of L-systems is to treat the textual description of a plant structure as a script, executable by a certain visualization module.

While there is no single “right” approach to interpret plant description strings, a commonly suggested way to get started is to treat individual characters as turtle commands.

 

 

import turtle
from dataclasses import dataclass


WIDTH = 1200
HEIGHT = 800
PEDESTRAL = 100

# a simple plant with a bud
AXIOM = "A"
RULES = {"A": "g[+A][-A]"}
ANGLE = 20
DISTANCE = 25
STEPS = 6

# the LRI plant with a bud
# AXIOM = "A"
# RULES = {"A": "AILR", "I": "g", "L": "[+g]", "R": "[-g]"}
# ANGLE = 30
# DISTANCE = 20
# STEPS = 4

# another example plant
# AXIOM = "X"  # "g"
# RULES = {"X": "g[+X]g[-X]+X", "g": "gg"}
# ANGLE = 40
# DISTANCE = 10
# STEPS = 4

# AXIOM = "X"
# RULES = {"X": "g-[[X]+X]+g[+gX]-X", "g": "gg"}
# ANGLE = 22.5
# DISTANCE = 10
# STEPS = 4

# AXIOM = "X"
# RULES = {"X": "g[+X]g[-X]+X", "g": "gg"}
# ANGLE = 25
# DISTANCE = 15
# STEPS = 4

# AXIOM = "g"
# RULES = {"g": "gg-[-g+g+g]+[+g-g-g]"}
# ANGLE = 22.5
# DISTANCE = 6
# STEPS = 4

# AXIOM = "X"
# RULES = {"X": "g[+X][-X]gX", "g": "gg"}
# ANGLE = 25.7
# DISTANCE = 3
# STEPS = 7

# AXIOM = "f"
# RULES = {"f": "f+g", "g": "f-g"}
# ANGLE = 90
# DISTANCE = 10
# STEPS = 7

# AXIOM = "g-g-g-g"
# RULES = {"g": "g-g+g+gg-g-g+g"}
# DISTANCE = 4
# ANGLE = 90
# STEPS = 3

# AXIOM = "g"
# RULES = {"g": "g[+g][-g]"}
# ANGLE = 20
# DISTANCE = 25
# STEPS = 6


def setup_screen(title):
    turtle.setup(WIDTH, HEIGHT)
    # turtle.tracer(0, 0)
    turtle.title(title)


@dataclass
class LSystem:
    script: str

    @classmethod
    def create(cls):
        r = cls(AXIOM)
        for i in range(STEPS):
            r.transform()
        return r

    def transform(self):
        self.script = "".join([self.apply_rule(c) for c in self.script])

    def apply_rule(self, c):
        return c if c not in RULES else RULES[c]

    def draw(self, drawer):
        while self.script:
            c = self.script[0]
            self.script = self.script[1:]

            if c.islower():
                drawer.forward(DISTANCE)
                turtle.update()
            elif c == "+":
                drawer.color("red")
                drawer.left(ANGLE)
            elif c == "-":
                drawer.color("green")
                drawer.right(ANGLE)
            elif c == "[":
                self.draw(drawer.clone())
            elif c == "]":
                return


setup_screen("L-systems")

drawer = turtle.Turtle()  # place at the bottom, point upward
drawer.color("blue")
drawer.hideturtle()
drawer.penup()
drawer.goto(0, -HEIGHT / 2 + PEDESTRAL)
drawer.left(90)
drawer.pendown()

LSystem.create().draw(drawer)

turtle.done()

 

 

  

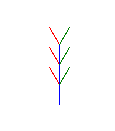
# the LRI plant with a bud
AXIOM = "A"
RULES = {"A": "AILR", "I": "g", "L": "[+g]", "R": "[-g]"}
ANGLE = 30
DISTANCE = 20
STEPS = 4

 

 

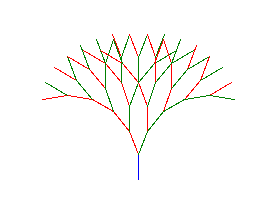
# another example plant
AXIOM = "X"  # "g"
RULES = {"X": "g[+X]g[-X]+X", "g": "gg"}
ANGLE = 40
DISTANCE = 10
STEPS = 4

 

 

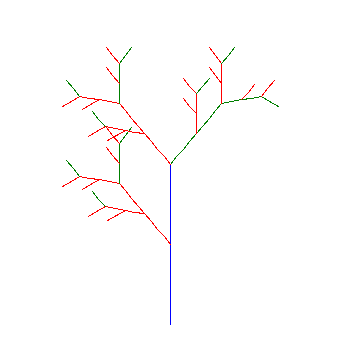
AXIOM = "X"
RULES = {"X": "g-[[X]+X]+g[+gX]-X", "g": "gg"}
ANGLE = 22.5
DISTANCE = 10
STEPS = 4

 

 

  

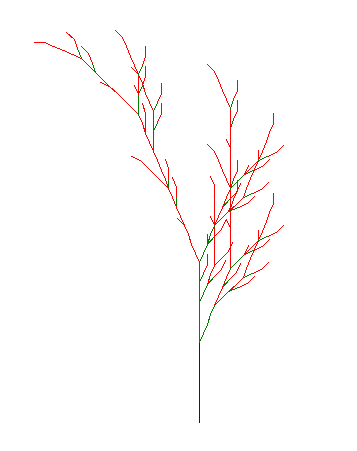
AXIOM = "X"
RULES = {"X": "g[+X]g[-X]+X", "g": "gg"}
ANGLE = 25
DISTANCE = 15
STEPS = 4

Step 1: g[+X]g[-X]+X
Step 2: gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X
Step 3: gggg[+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]gggg[-gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X
Step 4: gggggggg[+gggg[+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]gggg[-gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]gggggggg[-gggg[+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]gggg[-gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]+gggg[+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]gggg[-gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X]+gg[+g[+X]g[-X]+X]gg[-g[+X]g[-X]+X]+g[+X]g[-X]+X

 

AXIOM = "g"
RULES = {"g": "gg-[-g+g+g]+[+g-g-g]"}
ANGLE = 22.5
DISTANCE = 6
STEPS = 4

 

 

AXIOM = "X"
RULES = {"X": "g[+X][-X]gX", "g": "gg"}
ANGLE = 25.7
DISTANCE = 3
STEPS = 7

 

 

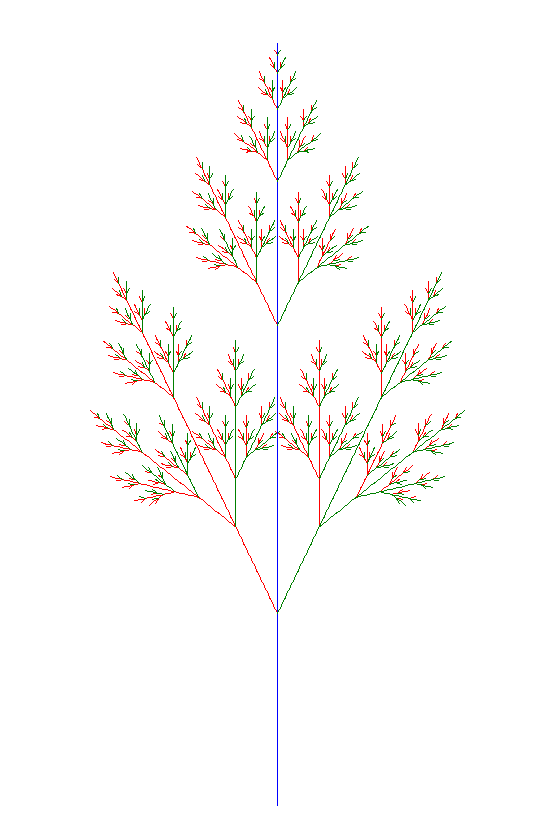
AXIOM = "f"
RULES = {"f": "f+g", "g": "f-g"}
ANGLE = 90
DISTANCE = 10
STEPS = 7

 

 

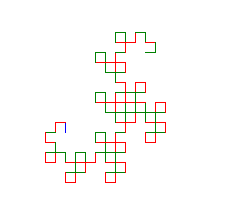
AXIOM = "g-g-g-g"
RULES = {"g": "g-g+g+gg-g-g+g"}
DISTANCE = 4
ANGLE = 90
STEPS = 3

 

 

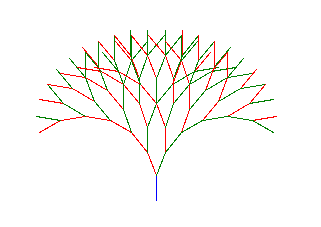
AXIOM = "g"
RULES = {"g": "g[+g][-g]"}
ANGLE = 20
DISTANCE = 25
STEPS = 6