1.13 - 动手学聚类算法

1. 基于距离的k-means聚类，需要人工提供聚簇数量K

1.1 通过肘方法确定最佳聚簇数量

 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs, load_iris
from sklearn.metrics import silhouette_score
import warnings

warnings.filterwarnings("ignore")
np.printoptions(suppress=True)

# 解决中文乱码
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 获取待聚簇数据
# 对鸢尾花数据集进行聚簇（众所周知，该数据有三类花朵）
X = load_iris(return_X_y=False).data
# 生成高斯聚簇分布的数据点, n_feature-样本特征数量; n_sample-样本数量
# X, y = make_blobs(n_samples=1500, n_features=2, centers=4, random_state=170)

# 2. 对待聚类数据归一化，不归一化，有的特征 数据过大会影响求解方差和最终聚簇结果。
x = StandardScaler().fit_transform(X)

# 3. 肘方法
scores1 = []
scores2 = []
for i in range(2, 8):
    # 通过 k-means 方法初始化聚簇质心，并重复实验 n_init 次，防止初始聚簇质心不好陷入局部最优
    model = KMeans(n_clusters=i, init='k-means++', n_init=10)
    model.fit(x)

    # model.cluster_centers_  # 查看聚簇质心

    # 1）按照轮廓系数选取最佳聚簇数K， 轮廓系数越大越好
    y = model.labels_  # 每个数据最终归纳到哪个簇
    score1 = silhouette_score(x, y)

    # 2）按照 聚簇方差损失 选取最佳聚簇数量，聚簇方差越小越好
    score2 = model.inertia_  # 各个点的聚簇方差总和

    scores1.append(score1)
    scores2.append(score2)

# 作图查看
plt.figure(num=1)
plt.plot(range(2, 8), scores1)
plt.xlabel("聚簇数量")
plt.ylabel("轮廓系数")
plt.title("肘方法 - 轮廓系数")

plt.figure(num=2)
plt.plot(range(2, 8), scores2)

plt.xlabel("聚簇数量")
plt.ylabel("所有数据点的方差和")
plt.title("肘方法 - 所有样本点聚簇方差总和")

# 显示图形
plt.show()

 

分析：

　　1）对于容易聚类的数据集如人工生成的，通过 轮廓系数和聚簇方差 都比较容易的选出最佳聚簇数K；但是对于比较难区分的数据集如鸢尾花数据集，很难看出来是三个簇。

　　2）上述代码实现，聚簇方差因为是每个样本点的方差总和，所以实际选取的最佳聚簇数K应该是 损失比较平滑的起点，而不是原理中的什么 幅度最大的那个。( 看图 )

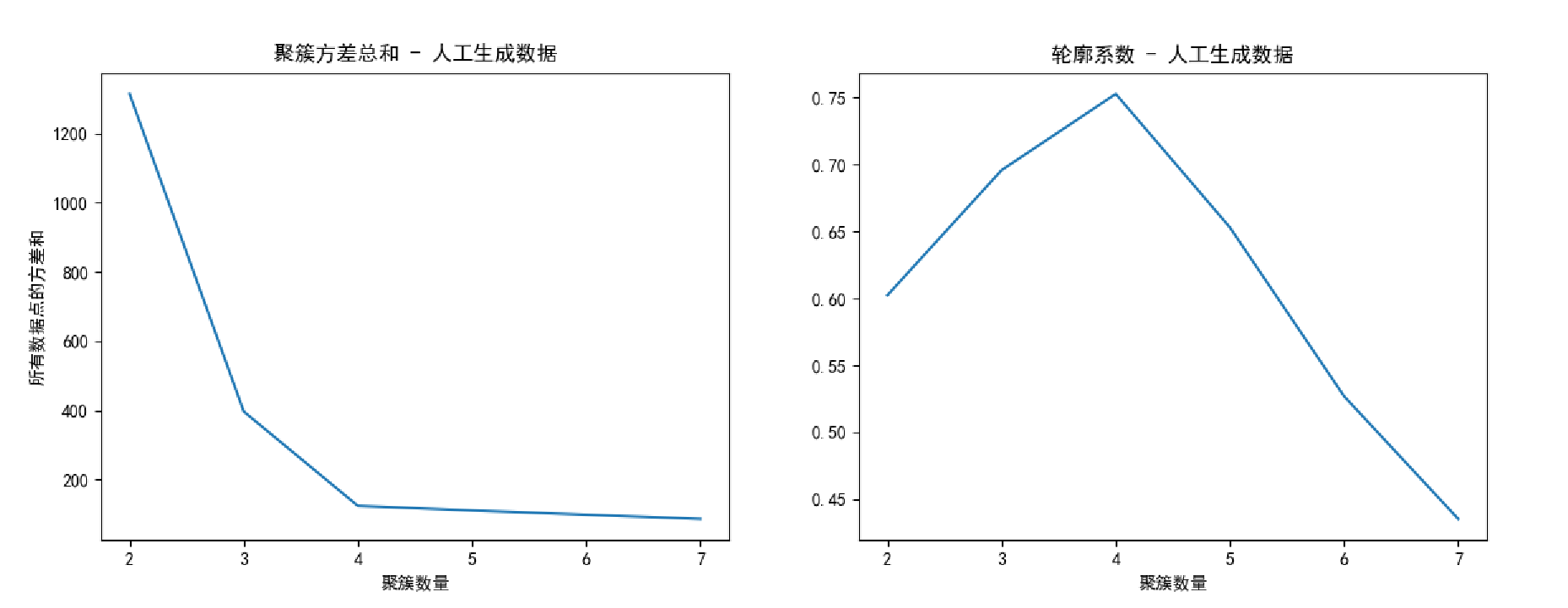
VS

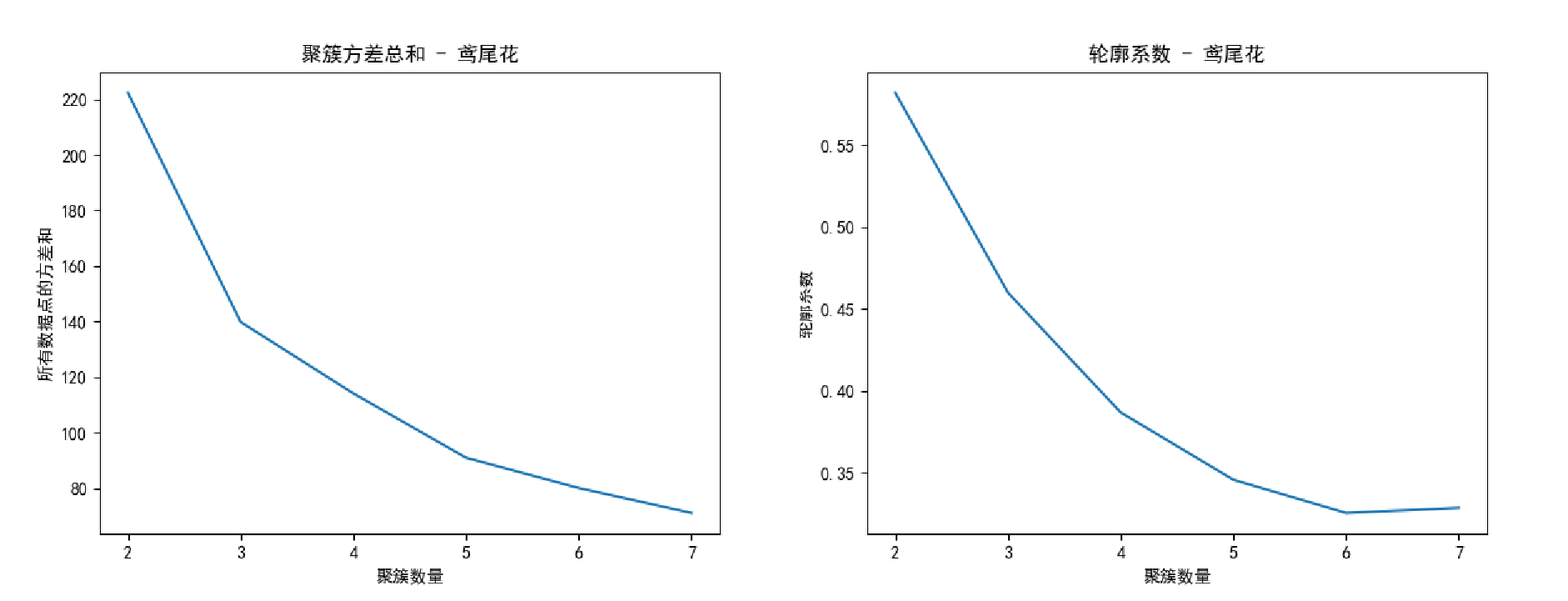
2. 基于密度的 DBSCAN 聚类

　　相比于前面的聚类方法，基于密度的聚类，如果超参数选好了效果还是相当不错的，但是一般选不好。所以 常用上面两个聚类而不用密度聚类。如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans, DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs, load_iris
from sklearn.metrics import silhouette_score
import warnings

warnings.filterwarnings("ignore")
np.printoptions(suppress=True)

x_iris = load_iris(return_X_y=False).data
x_gauss, y = make_blobs(n_samples=1500, n_features=2, centers=4, random_state=170)

x_iris = StandardScaler().fit_transform(x_iris)
x_gauss = StandardScaler().fit_transform(x_gauss)

model = DBSCAN(eps=0.5, min_samples=5)
labels_iris = model.fit_predict(x_iris)
labels_gauss = model.fit_predict(x_gauss)

print('DBSCAN算法在鸢尾花数据集上最终聚簇为{}类'.format(len(np.unique(labels_iris))))  # 3 簇
print('DBSCAN算法在人生生成Gauss数据集上最终聚簇为{}类'.format(len(np.unique(labels_gauss))))  # 2 簇

分析：最终鸢尾花聚簇数为 3，人工生成Gauss分布数据集聚簇数为 2 ，显然很扯淡。