Bellman-Ford算法

定义

Bellman-Ford算法比Dijkstra算法更具有普遍性，因为它对边没有要求，可以处理负权边并可以判断是否存在负权环。缺点是时间复杂度过高，为O（VE），v-1轮松弛操作。

问题描述：在无向有权图G = （V，E）中，假设每条边E[i]的长度是w[i],找到由顶点V0到其余各点的最短路径。

负权环

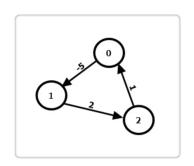
 如上图所示，这就是一个负权环，可以无限循环直到负无穷。

循环次数	dis[0]	dis[1]	dis[2]
第一次	0	-5	Max
第二次	0	-5	-3
第三次	-2	-7	-5

提前说一下：Bellman-Ford判断存在负权环的依据是：在已经循环V - 1次松弛操作的基础上，再做一轮松弛操作，如果dis最短距离仍会更新（有松弛成功的边），那么就说明存在负权环。

松弛操作

先理解一段话，在Dijkstra算法中，核心思想是贪心，即所求得的dis[i]中最短的顶点i必定是无法继续缩短（松弛）源点到其距离的顶点，因为如果说要继续缩短（松弛）源点到点i的距离，那么必定要绕过其他点，但是Dijkstra的潜在条件就是没有负权边，无法对其松弛（缩短）所以这种方法是有效的。

好了，脑海里一定对松弛有了自己的定义，即对每个边e(a, b)，将源点v到b的距离更新为：原来源点v到b的距离和源点v到a的距离加上a到b的距离中较小的那个。

If(dis[a] + ab < dis[b])
   dis[b] = dis[a] + ab

路径松弛性质

假设p = (v0,v1,v2...,vk)是从源点v到目标节点vk的一条最短路径，并且我们对p中的边进行松弛操作的顺序为(v0,v1)(v1,v2)...(vk - 1, vk)，那么这些松弛操作结束后的d[k],必定是源点v到点vk的最短路径！该性质的成立，与其他的松弛操作无关。

如果要证明上面的性质，那么必须了解下面的性质：

松弛操作的收敛性质：设f[vi]是源点v到点vi的最短路径长度，dv[i]是源点v到点vi的当前最短路径，对于节点a,b属于V。如果s->...->a->b为一条v到b的最短路径，且在对边(a,b)进行松弛操作之前有f[a] = d[a]，则必有：在对边(a,b)松弛之后f[b] = d[b]。

定义：p为源点到点vk的一条最短路径，vi代表p中第i条边的结束节点。假设最短路p的第i条边背松弛之后d[vi] = f[vi]。i = 0时，就是d[v0] = f[0] = 0;那么归纳：假设d[vi - 1] = f[vi - 1]成立，根据松弛操作的收敛性质，再对边（vi - 1， vi）进行松弛之后，满足f[vi] = d[vi]。 

算法描述

对所有边进行V - 1轮松弛操作，因为在一个含有V个顶点的图中，任意两点之间的最短路径最多包含V-1边。换句话说，第一轮对所有边进行松弛后，得到的是源点最多经过一条边到达其他顶点的最短距离；第二轮在对所有边进行松弛后，得到的是源点最多经过两条边到达其他顶点的最短距离；第三轮在对所有边进行松弛后，得到的是源点最多经过三条边到达其他顶点的最短距离。

不仅针对有向图，无向图中也可以使用。

可以求解不包含负权环的最短路，经过V-1轮松弛操作

如果再进行一次操作还能更新最短路的话，那么就说明存在负权环。

代码

#include <iostream>
#include <fstream>
#include <vector>
#include <queue>
#include <bitset>

#define MAXN 50005
#define FIN "bellmanford.in"
#define FOUT "bellmanford.out"
#define oo ((1LL << 31) - 1)
using namespace std;
int nodes;
int edges;
int disMin[MAXN];
vector<pair<int, int>> Graph[MAXN];
bitset<MAXN> visited;

void readData() {
    int x, y, cost;
    fstream fin(FIN);
    fin >> nodes >> edges;
    int tmp = edges;
    while (tmp--) {
        fin >> x >> y >> cost;
        Graph[x].push_back({y, cost});
        Graph[y].push_back({x, cost});
    }
    fin.close();
}

bool bellmanFord(int source) {
    for (int n = 1; n <= nodes; n++) {
        disMin[n] = oo;
    }
    disMin[source] = 0;
    for (int v = 0; v < nodes - 1; v++) {
        for (int i = 1; i <= nodes; i++) {
            for (auto edge : Graph[i]) {
                if (disMin[i] != oo && disMin[edge.first] > disMin[i] + edge.second)
                    disMin[edge.first] = disMin[i] + edge.second;
            }
        }
    }

    for (int i = 1; i <= nodes; i++) {
        for (auto edge : Graph[i]) {
            if (disMin[i] != oo && disMin[edge.first] > disMin[i] + edge.second)
                return false;
        }
    }
    return true;
}

void writeData() {
    ofstream fout(FOUT);
    for (int i = 2; i <= nodes; ++i)
        (disMin[i] < oo) ? fout << i << ": " << disMin[i] << endl : fout << i << ": " << 0 << endl;
    fout.close();
}

int main() {
    readData();
    bellmanFord(1);
    writeData();
    return 0;
}

测试用例

5 8
1 2 4
1 3 2
2 3 1
2 4 2
2 5 3
3 4 5
3 5 5
4 5 1

起始点设为1，结果为

2: 3
3: 2
4: 5
5: 6

如果更改测试用例

5 8
1 2 -1
1 3 2
2 3 1
2 4 2
2 5 3
3 4 5
3 5 5
4 5 1

检测到负权环