数据结构与算法 01、 基本认知 & 线性表初探

本文用来了解数据结构与算法的一些基础。

书籍推荐：《大话数据结构 - 程杰 著》

一、算法

1、算法特性

算法：解决特定问题的一步步思路方法步骤。在计算机中其表现在指令的有限序列，每个指令包含一或多个操作。

算法特性：

• 有输入输出
• 有穷性 - 有限步骤内完成，不能无限循环
• 确定性 - 有确定结果，不能存异
• 可行性 - 每一行代码必须示可执行的　　

算法的设计要求：

• 正确性 - 
• 可读性 - 
• 健壮性 - 
• 时间效率高&存储量低

2、算法的复杂度

大O表示法

• 用常数1取代运行时间中所有常数 3 --> O(1)
• 运行次数函数中，只保留最高阶 n³+2n²+3 --> O(n³)
• 最高阶存在且不等于1时，去除与这个高阶项 相乘的常数 3n3+2n2+n+4 --> O(n3)

1、时间复杂度

时间复杂度术语:

• 常数阶 - 3
• 对数阶 - log_aⁿ  --> 以 a 为底 n 的对数 a^x=n, x=log_aⁿ 
• 线性阶 - 2n+1
• 平方阶 - n²
• 立方阶 - n³
• nlog 阶 - n*logn 即 n * log₂ⁿ. 一般以2为底习惯性省略2的书写.  
• 指数阶 - O(2ⁿ) 或者 O(n!) --> 一般不考虑！除非是 n 非常的小，否则会造成可怕的噩梦般的时间消耗。这是一种不切实际的算法时间复杂度，一般不会考虑。

1. 示例

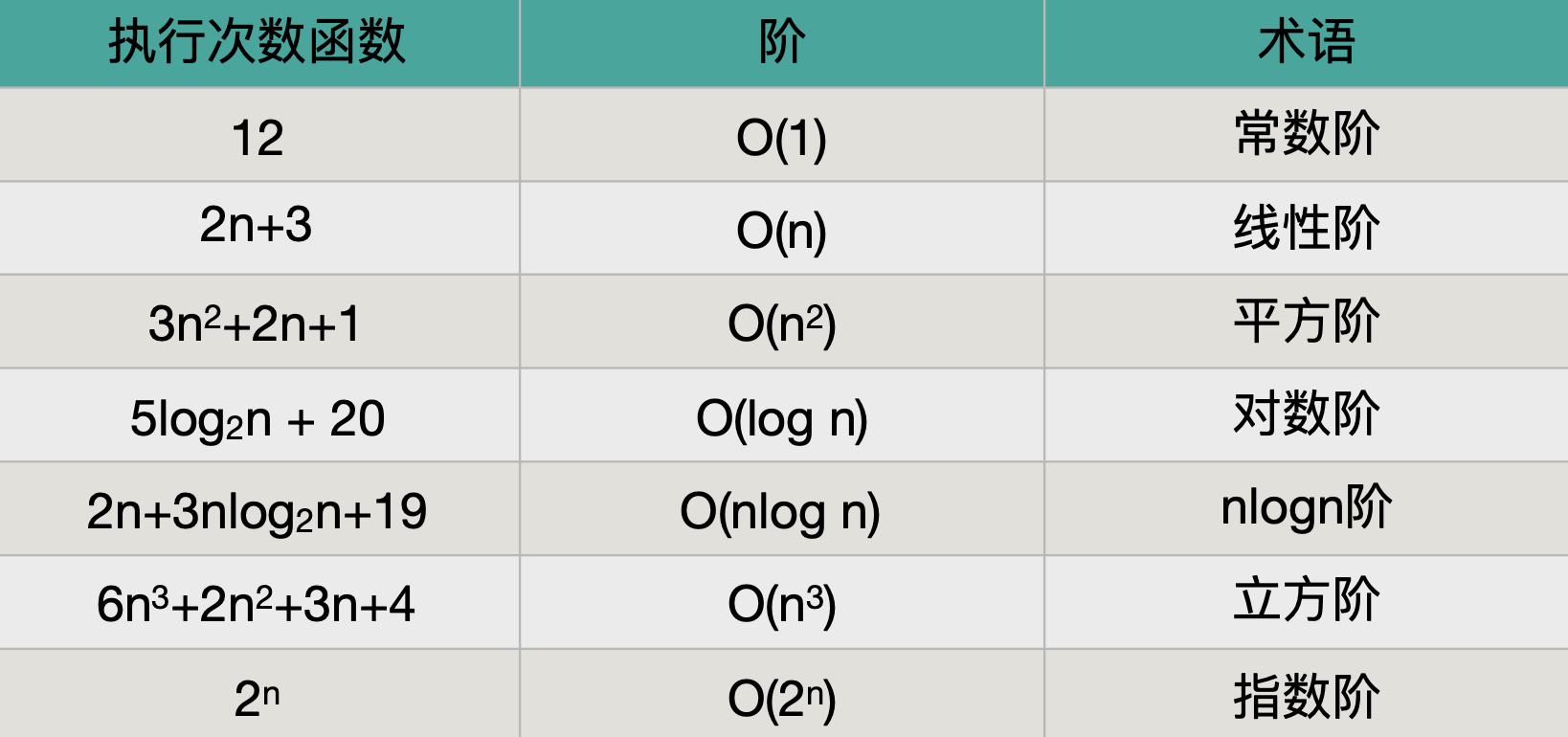
时间复杂度大小关系：O(1) < O(logⁿ) < O(n) < O(nlogⁿ) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

2. 代码示例

常数阶：

// 常数阶时间复杂度计算 O(1) <-- 常数用 1 代替
// 1+1+1 = 3 --> O(1)
void testSum1(int n){
    int sum = 0;                // 执行1次
    sum = (1+n)*n/2;            // 执行1次
    printf("testSum1:%d\n",sum);// 执行1次
}

// 1+1+1+1+1+1+1 = 7 --> O(1)
void testSum2(int n){
    int sum = 0;                // 执行1次
    sum = (1+n)*n/2;            // 执行1次
    sum = (1+n)*n/2;            // 执行1次
    sum = (1+n)*n/2;            // 执行1次
    sum = (1+n)*n/2;            // 执行1次
    sum = (1+n)*n/2;            // 执行1次
    printf("testSum2:%d\n",sum);// 执行1次
}
// x=x+1; --> 执行1次
void add(int x){
    x = x+1;
}

对数阶：

// 对数阶 -- 不论是 以几为底n的对数，都会归到 logn 表示
// 2的x次方等于n x = log2n --> O(logn)
void testA(int n){
    int count = 1;         //执行1次
    // n = 10
    while (count < n) {
        count = count * 2;
    }
}

// 5的x次方等于n x = log5n  --> O(logn)
void testF(int n){
    int count = 1;         //执行1次
    // n = 100
    while (count < n) {
        count = count * 5;
    }
}

线性阶：

// 线性阶时间复杂度 
// x=x+1; 执行n次 --> O(n)
void add2(int x,int n){
    for (int i = 0; i < n; i++) {
        x = x+1;
    }
}

// 1+(n+1)+n+1 = 3+2n --> O(n)
void testSum3(int n){
    int i,sum = 0;               // 执行1次
    for (i = 1; i <= n; i++) {   // 执行n+1次
        sum += i;                // 执行n次
    }
    printf("testSum3:%d\n",sum); // 执行1次
}

平方阶：

// 平方阶
// x=x+1; 执行 n*n 次 --> O(n^2)
void add3(int x,int n){
    for (int i = 0; i< n; i++) {
        for (int j = 0; j < n ; j++) {
            x=x+1;
        }
    }
}

// n+(n-1)+(n-2)+...+1 = n(n-1)/2 = n^2 / 2 + n/2 --> O(n^2)
// 等差数列公式：sn = n(a1+an)/2 <-- (1+100)*100/2 = 5050
void testSum4(int n){
    int sum = 0;
    for(int i = 0; i < n;i++)
        for (int j = i; j < n; j++) {
            sum += j;
        }
    printf("textSum4:%d",sum);
}

// 1+(n+1)+n(n+1)+n^2+n^2 = 2+3n^2+2n --> O(n^2)
void testSum5(int n){
    int i,j,x=0,sum = 0;           // 执行1次
    for (i = 1; i <= n; i++) {     // 执行n+1次
        for (j = 1; j <= n; j++) { // 执行n(n+1)
            x++;                   // 执行n*n次
            sum = sum + x;         // 执行n*n次
        }
    }
    printf("testSum5:%d\n",sum);
}

立方阶：

// 立方阶
void testB(int n){
    int sum = 1;                         // 执行1次
    for (int i = 0; i < n; i++) {        // 执行n次
        for (int j = 0 ; j < n; j++) {   // 执行n*n次
            for (int k = 0; k < n; k++) {// 执行n*n*n次
                sum = sum * 2;           // 执行n*n*n次
            }
        }
    }
}

3. 时间复杂度的大小

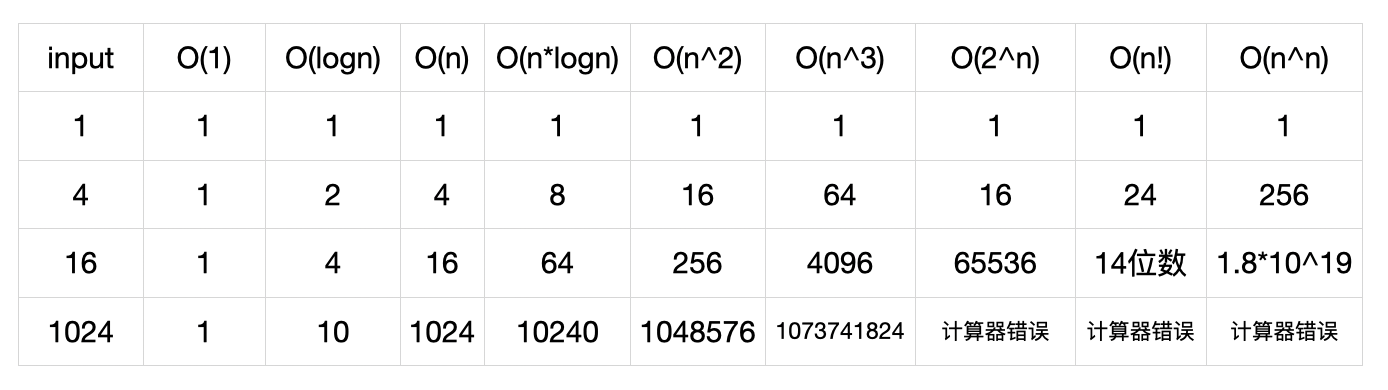
2、空间复杂度

空间复杂度：计算算法过程中，中间变量所需的存储空间。

公式 S(n) = n(f(n)) --> n：问题的规模; f(n)：关于 n 所占存储空间的函数

程序空间计算考虑因素:

• 寄存本身的指令
• 常数
• 变量
• 输入
• 对数据进行操作的辅助空间

在考量算法的空间复杂度时，主要考虑的是算法执行时所需要的辅助空间。

代码示例：

// 数组逆序,将一维数组 a 中的 n 个数逆序存放在原数组中.
int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
   
    int n = 5;
    int a[10] = {1,2,3,4,5,6,7,8,9,10};
    
    // 算法实现1 --> O(1)
    int temp;// 1中间变量
    for(int i = 0; i < n/2 ; i++) {
        temp = a[i];
        a[i] = a[n-i-1];
        a[n-i-1] = temp;
    }
    for(int i = 0;i < 10;i++) {
        printf("%d\n",a[i]);
    }
    
    // 算法实现2 --> O(n)
    int b[10] = {0};// n
    for(int i = 0; i < n;i++) {
        b[i] = a[n-i-1];// n个中间值
    }
    for(int i = 0; i < n; i++) {
        a[i] = b[i];
    }
    for(int i = 0;i < 10;i++) {
        printf("%d\n",a[i]);
    }
    
    return 0;
}

二、数据结构 概念

文章 数据结构与算法 0 中对数据结构的一些基本概念进行了简单了解，这里进行更详细的介绍。

1、基本数据单位

 

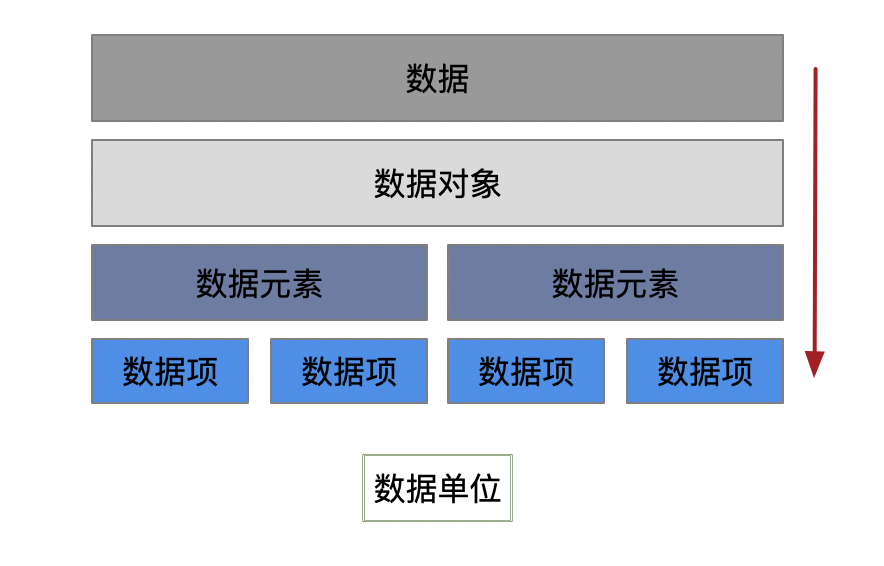
2、逻辑结构与物理结构

1）逻辑结构

逻辑结构，描述的是数据元素之间的相互关系。它只是代表数据间所存在的一个逻辑关系，例如：人与人、树干与树枝等。

1. 集合结构

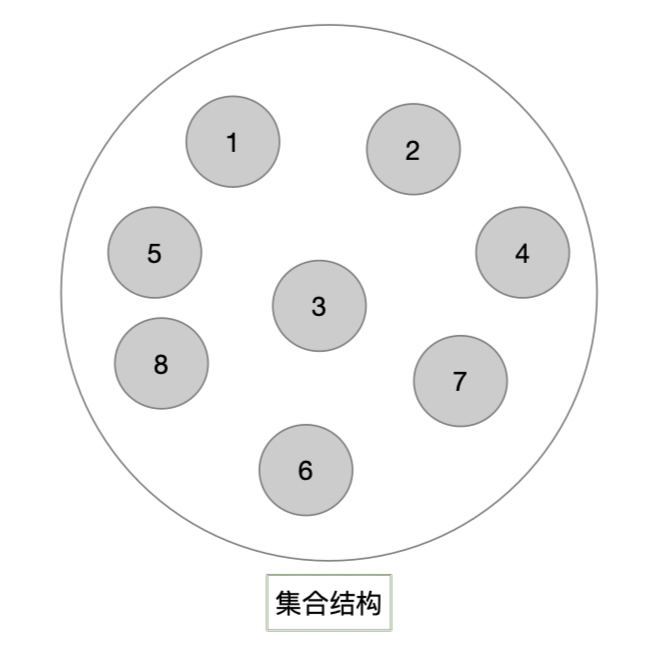
集合结构：同属于一类但并无什么特定关系。例：动物便是一个集合，包含人、猫猫、狗狗...；植物也是一个集合，花草树木...。 

2. 线性结构

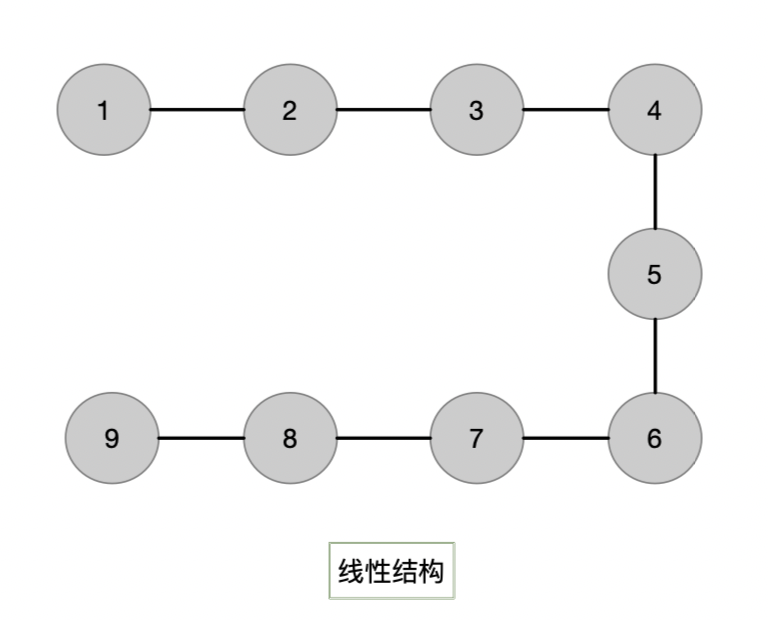
线性结构：数据与数据间符合一对一的关系。

常见线性结构：线性表、链表、数组、字符串(多个字符组合而成)；

　　　　　　　队列、栈 因其特殊的读取方式，属于特殊的线性结构。

3. 树结构

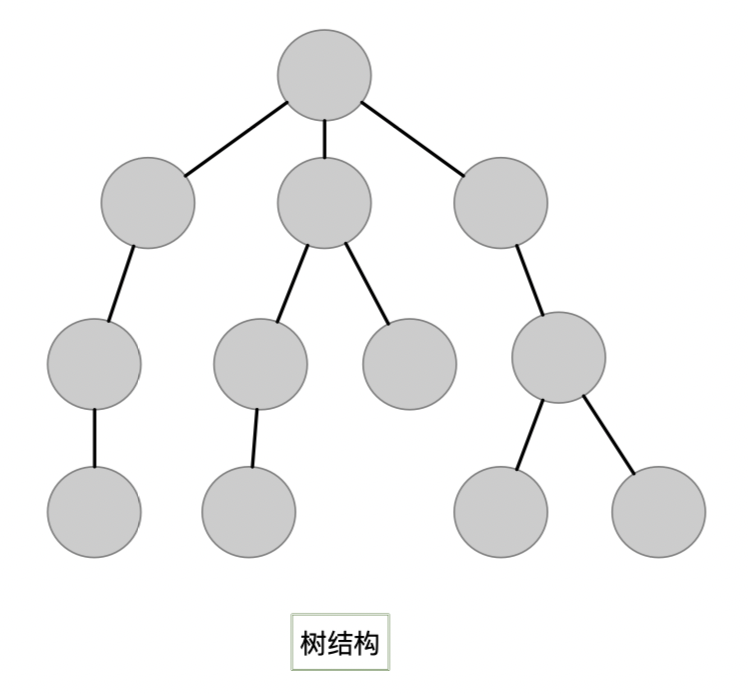
树结构特点：数据关系之间是一对多的关系。

4. 图形结构

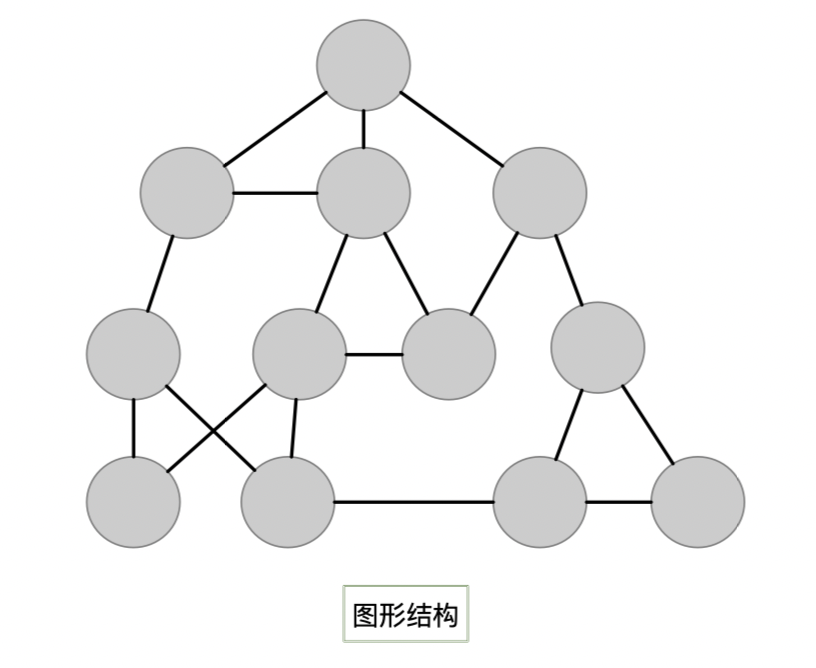
图形结构特点：数据与数据间多对多的关系。 

2）物理结构(也称存储结构)

物理结构：指数据的逻辑结构在计算机中的存储形式。

数据是数据元素的集合，那么物理结构实际上就是：如何把数据元素存储到计算机的存储器中。存储器是针对内存而言的。(硬盘、软盘、光盘等外部存储器的数据组织通常用文件结构来描述。)

对于所有数据，最终它们都是需要存储到计算机内存中去的，数据元素在内存中的存储方式(存储结构形式)有 2 种：顺序存储 链式存储。

1. 顺序存储结构

开辟一段连续的内存空间，按顺序依次存储进去，其数据间的逻辑关系和物理关系是一致的。简单来说就是：排队占位。按序排好队，每人占一小段空间。例：数组 arr[10].

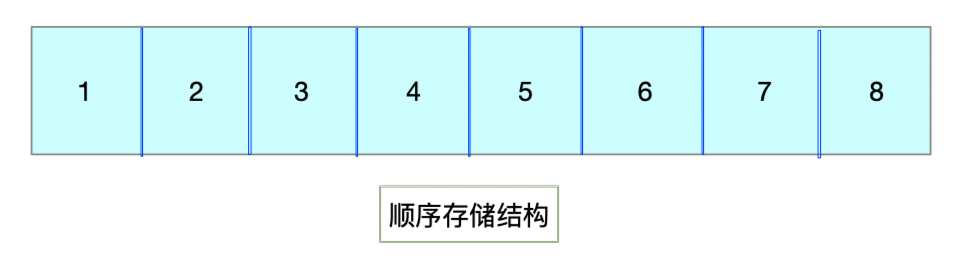
优点：查询快；

缺点：增删麻烦，每次都需要对数据进行重新的排序。

2. 链式存储结构

链式存储结构：把数据元素存放在任意的存储单元里，这组存储单元可以是连续的也可不连续，即：不需要提前开辟连续的内存空间。

这种数据元素的存储关系并不能反映其逻辑关系，因此需要用一个指针存放数据元素的地址，这样就可以通过地址找到相关元素的位置。

 

优点：增删便捷，增加找到位置放进去即可，删除后删除的元素需要释放为nil防止野指针；

缺点：查询很慢。

3、抽象数据类型

1. 数据类型

数据类型：是指一组性质相同的值的集合 以及 定义子在此集合上的一些操作的总称。

数据类型是按照值的不同进行划分的。在 C 语言中，按照值的不同，数据类型可分为 2 类：

• 原子类型：不可再分解的基本类型，包括：整型、实型、字符型等；
• 结构类型：由若干个类型组合而成，可以再分解。例如：整形数组，它是由若干整型数据组成的。

例如 int a ,b; 这意味着 在给变量 a、b 赋值时不能超出 int 的取值范围，且变量之间的运算只能是 int 类型所允许的运算。

因不同计算机不同的硬件系统，编程语言最终都会被编译成底层语言。然而对于高级语言来讲，目的知识实现 a+b 的运算，不关心计算机内部或 CPU 都具体做了什么，这里其实就引出了 抽象 的概念。

抽象：是指抽取出事物具有的普遍性的本质。它抽出问题的特征而忽略非本质的细节，相当于是对一个具体事物的概括。即：隐藏了繁杂的细节，保留实现目标所必须的信息。例如：一本书籍的章节目录。

2. 抽象数据类型

抽象数据类型(Abstract Data Type, ADT)：指 一个数学模型 及其 定义在该模型上的一组操作。抽象数据类型的定义仅仅取决于它的一组逻辑特性，与计算及内部如何表示和实现无关。

比如上述的 整型 int 的例子，各个计算机，不论电脑、pad、手机等等，都拥有“整型”类型，也需要证书间的运算，so 整型 其实就是一个抽象数据类型。

除了已定义并实现的，抽象数据类型还包括编程者自己定义的数据类型，如坐标，定义一个 point 的抽象数据类型，它有 x、y、z 三个整型变量，我们就可以通过 point 数据变量来知道这一点的坐标。

抽象数据类型体现了程序设计中 问题分解、抽象和信息隐藏的特性。

描述抽象数据类型的标准格式：

/**描述抽象数据类型的标准格式
    ADT  抽象数据类型名
    Data
        数据元素之间的逻辑关系定义
    Operation
        操作1
            初始条件
            操作结果描述
        操作2
            ... ...
        操作 n
            ... ...
    endADT
 */

三、线性表的存储方式

线性表(List)：零个或多个数据元素的有序序列。有序 有限.

如下图，将线性表用数学语言进行定义，记为：(a₁, ..., a_i-1, a_i, a_i+1, ..., a_n)，则表中 a_i-1 领先于 a_i, a_i 领先于 a_i+1，称 a_i-1 是 ai 的直接前驱元素，a_i+1 是 a_i 的直接后继元素。当 i=1,2,...,n-1 时，a_i 有且仅有一个直接后继，当 i=2,3,...,n 时，a_i 有且仅有一个直接前驱。

由上可知，线性表元素的个数 n(n≥0) 定义为线性表的长度，当 n=0 时，称为空表。 

对于非空的线性表和线性结构，特点如下：

• 存在唯一的一个被称作“第一个”的数据元素；
• 存在唯一的一个被称作“最后一个”的数据元素；
• 除了第一个之外，结构中的每个元素都有一个前驱；
• 除了最后一个外，结构中的每个元素都有一个后继。

线性表的抽象数据类型：

/**线性表的抽象数据类型定义
   ADT  线性表 (List)
   Data
       线性表的数据对象集合为{a1, a2,  ..., an}，每个元素的类型均为 DataType。其中，除第一个元素 a1 外，每个元素都有且仅有一个直接前驱元素，除最后一个元素 an 外，每个元素都有且仅有一个直接后继元素。数据元素之间的关系是一对一。
   Operation
       InitList (*L) ：初始化操作，建立一个空的线性表 L
       ListEmpty (L) ：若线性表为空，返回 true，否则返回 false
       ClearList (L) ：将线性表清空
       GetElem(L, i, *e) ： 将线性表 L 的第 i 个位置元素值返回给 e
       LocateElem(L, e) ： 在线性表 L 中查找与给定值 e 相等的元素，成功返回该元素在表中序号；否则返回 0 表示查找失败
       ListInsert(*L, i, e) ： 在线性表 L 中 第 i 个位置插入新元素 e
       ListDelete(*L, i, *e) ： 删除线性表 L 中 第 i 个位置元素，并用 e 返回其值
       ListLength(L) ：返回 线性表 L 的元素个数
   endADT
*/

1、线性表的顺序存储

线性表的顺序存储结构，指 用一段地址连续的存储单元依次存储线性表的数据元素。

1. 代码示例

顺序存储的线性表，创建、初始化和增删：

/// 顺序存储的线性表

#define MAXSize 100

typedef struct {
    int *data;
    int length;
}MyList;

MyList gList;

// 初始化一个线性表
int initList(MyList *L) {
    
    L->data = malloc(sizeof(MyList)*MAXSize);
    if (!L->data) {// 若分配空间失败，退出
        exit(0);
    }
    L->length = 0;// 空表长度0
    return 1;
}

// 线性表的插入
/**
 在 L 中 的 i 位置 添加插入 ele
 插入位置的后面的元素都要后移一位
 */
int insertList(MyList *L, int i, int ele) {
    
    if (i < 0 || i > L->length + 1) {// 位置合法
        exit(0);
    }
    if (L->length == MAXSize) {// 最大空间已满
        return 0;
    }
    
    if (i <= L->length) {
        for (int j = L->length-1; j >= i; j--) {
            // 添加的元素 i 位置后的元素都后移一位
            L->data[j+1] = L->data[j];
        }
    }
    L->data[i] = ele;
    ++L->length;// 表长度+1
    return 1;
}

// 线性表的取值
// 取某个值
int getElemFrmList(MyList L, int i, int *elem) {
    
    if (i < 0 || i > L.length + 1) {// 位置合法
        exit(0);
    }
    *elem = L.data[i-1];
    return 1;
}
// 打印全部值
int getAllEleFormList(MyList l){
    for (int i=0; i<l.length; i++) {
        printf("-- list的%d元素：%d --\n",i,l.data[i]);
    }
    return 1;
}

// 删除
int deleteList(MyList *L, int i, int *ele) {
    
    if (L->length==0 || i < 0 || i > L->length + 1) {//线性表不为空 / 位置合法
        exit(0);
    }
    *ele = L->data[i];
    for (int j = i; j<L->length; j++) {
        // 删除元素的位置开始，后面的元素依次向前一位
        L->data[j] = L->data[j+1];
    }
    --L->length;// 表长度-1
    return 1;
}

// 清空
int clearList(MyList *l) {
    l->length = 0;
    return 1;
}

int main(int argc, const char * argv[]) {
    @autoreleasepool {
        // insert code here...
        NSLog(@"Hello, World!");
        
        
        MyList L;
        int status;
        
        // 初始化
        status = initList(&L);
        printf("初始化的线性表 length=%d\n",L.length);// 0
        // 插入
        for (int i=0; i<5; i++) {
            status = insertList(&L,i,i+10);// 10 11 12 13 14
        }
        printf("线性表 length=%d\n",L.length);// 5
        // 取值
        int ele;// 变化的数据用它的指针来指
        status = getElemFrmList(L, 2, &ele);
        printf("线性表的第2个元素=%d\n",ele);// 11
        getAllEleFormList(L);
        // 删除元素
        status = deleteList(&L, 3, &ele);
        printf("线性表的删除的第3个元素是=%d length=%d\n",ele,L.length);// 13
        // 清空list 里的元素
        status = clearList(&L);
        printf("线性表 length=%d\n",L.length);// 0        
    }
    return 200;
}

2. 线性表顺序存储结构的优缺点

优点：

• 无需额外为表示表中元素之间的逻辑关系而增加额外的存储空间；
• 可以快速的存取表中任一位置的元素。

缺点：

• 插入和删除操作需要移动大量元素；
• 当线性表长度变化较大时，难以确定存储空间的容量；
• 造成存储空间碎片。

2、线性表的链式存储

我们已知顺序存储的最大缺点是插入删除时需要移动大量数据元素，这显然是要耗时的，如何解决呢？--> 链式存储结构

文章 数据结构与算法 0 中链表部分有通过简单图形介绍无头结点的链表结构。

1. 带有头结点的链表：

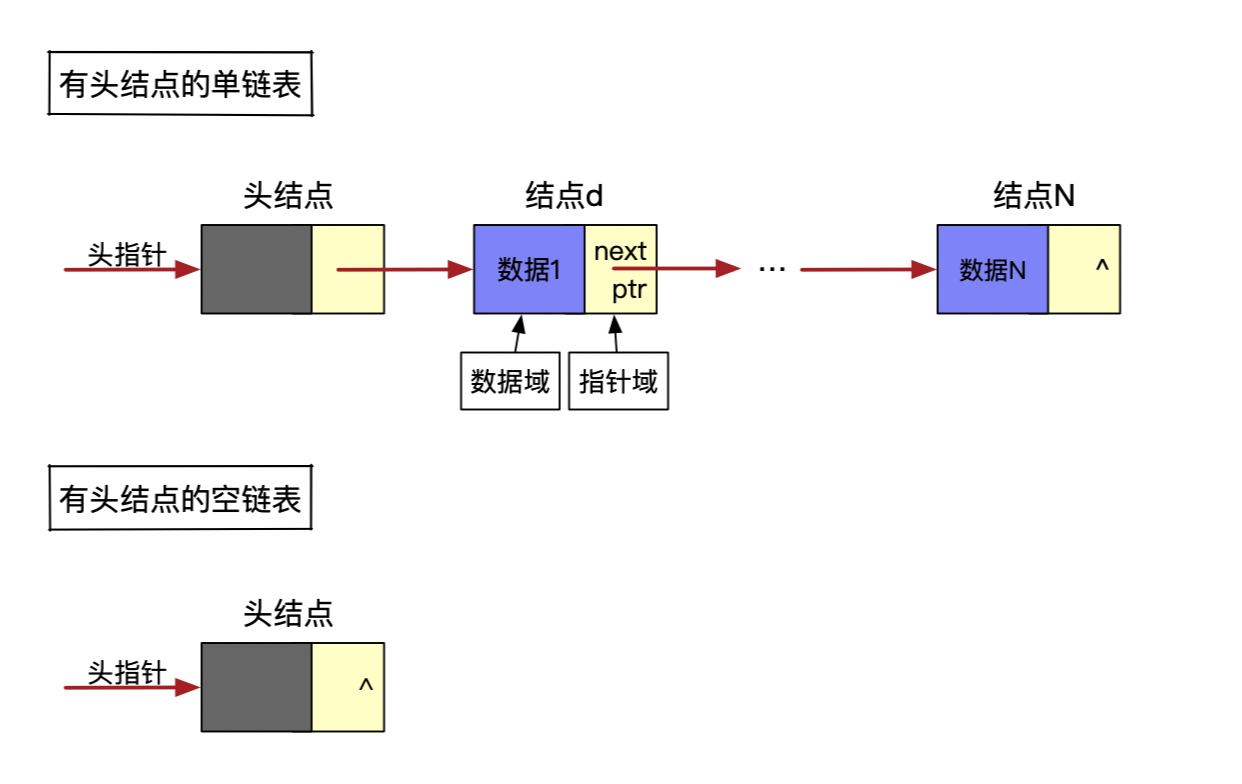
2. 代码示例

1）带有头结点的单链表的 创建初始化、插入、删除、取值、遍历：

// 方便起见，类型 typedef 一下
typedef struct Node {
    
    int data;
    struct Node *next;
} Node;
typedef struct Node * linkedList;

// 初始化一个空链表
int func_initLinkedList(linkedList *L) {
    
    *L = (linkedList)malloc(sizeof(Node));
    if (*L == NULL) {
        return 0;
    }
    (*L)->next = NULL;
    return 200;
}

// 单链表插入数据
int func_insertLinkedList (linkedList *L, int i, int e) {
    
    linkedList p,s;
    p = *L;
    
    int j = 1;

    // 找到要插入位置的前一个结点
    while (p && j<i) {
       p = p->next;
        ++j;
    }
    if (!p || j>i) {// p不存在 或 插入位置不合法
        return 0;
    }
    
    // 建一个新节点
    s = (linkedList)malloc(sizeof(Node));
    s->data = e;
    // 新结点 s 的 next 指向 p的后继
    s->next = p->next;
    // p 的后继指向 新结点 s
    p->next = s;
    return 200;
}

// 取值
int func_getElem(linkedList L, int i, int *e) {
    
    int j;
    linkedList p;
    p = L->next;
    j = 1;
    while (p && j<i) {
        p = p->next;
        j++;
    }
    if (!p || j>i) {// p不存在 或 插入位置不合法
        return 0;
    }
    *e = p->data;
    return 200;
}

// 遍历
int func_allElem(linkedList L) {
    
    linkedList p;
    p = L->next;
    
    while (p) {
        printf("getall: %d\n",p->data);/**
                                        getall: 9
                                        getall: 8
                                        getall: 7
                                        getall: 6
                                        getall: 5
                                        getall: 4
                                        getall: 3
                                        getall: 2
                                        getall: 1
                                        */
        p = p->next;
    }
    return 200;
}
// 删除结点
int func_deleteNode(linkedList *L, int i, int *e) {
    
    linkedList p,s;
    int j = 1;
    p = (*L)->next;
    
    // 找到要删除结点的前一个结点
    while (p->next && j<(i-1)) {
        p = p->next;
        ++j;
    }
    if (!(p->next) || j>i-1) {// p不存在 或 删除位置不合法
        return 0;
    }
    
    s = p->next;// 要删除的结点 s
    p->next = s->next;
    
    *e = s->data;
    free(s);
    
    return 200;
}


// 链式存储的线性表
void func_linkedList (){
    
    linkedList L;
    struct Node *L1;
    func_initLinkedList(&L);
    func_initLinkedList(&L1);

    for (int i = 1; i<10; i++) {
        func_insertLinkedList(&L, 1, i);
    }// L：9 8 7 6 5 4 3 2 1
    
    int e;
    func_getElem(L,3,&e);
    printf("e: %d\n",e);// e: 7

    func_allElem(L);
    
    int e1;
    // 删除第 4 个
    func_deleteNode(&L, 4, &e1);
    printf("e1: %d\n",e1);// e1: 6
    func_allElem(L);

}

2）单链表头插法和尾插法：

// 头插法 - 插入n个结点
int func_addHead(linkedList *L,int n) {
    
    // 建立带头结点的单链表
    *L = (linkedList)malloc(sizeof(Node));
    (*L)->next = NULL;
    
    linkedList p;
    for (int i=0; i<n; i++) {
        
        p = (linkedList)malloc(sizeof(Node));
        p->data = i;
        p->next = (*L)->next;
        (*L)->next = p;
    }
    return 200;
}
// 尾插法
int func_addTail (linkedList *L,int n) {
    
    // 建立带头结点的单链表
    *L = (linkedList)malloc(sizeof(Node));
    (*L)->next = NULL;
    linkedList t;
    t = *L;// t 为尾结点
    
    linkedList p;
    for (int i=0; i<n; i++) {
        p = (linkedList)malloc(sizeof(Node));
        p->data = i;

        t->next = p;
        t = p;
    }
    t->next = NULL;
    
    return 200;
}

// 调用
    printf("\n");
    // 头插法
    linkedList L3;
    func_addHead(&L3, 10);
    func_allElem(L3);// 9 8 7 6 5 4 3 2 1 0

    printf("\n");

    // 尾插法
    linkedList L4;
    func_addTail(&L4, 10);
    func_allElem(L4);// 0 1 2 3 4 5 6 7 8 9

3）清空链表

// 清空链表
int func_clearLinkedList(linkedList *L){
    
    linkedList p,tmp;
    p = (*L)->next;// p 指向第一个结点
    while (p) {
        tmp = p->next;
        free(p);
        p = tmp;
    }
    (*L)->next = NULL;// 头结点指针域置为空
    return 200;
}

以上。