数据结构与算法 0、 汇总简介

数据结构 是指 互相之间存在一种或多种关系的数据元素的集合。数据元素之间存在的一or多种特定关系，也就是数据的组织形式。

数据：即符号，可以输入到计算机并被计算机程序处理。

　　例：整型、字符等数值类型可以进行数值/非数值运算；声音、图像、视频等通过编码手段转成字符数据处理。

数据元素：组成数据的基本单位。

　　例：动物中数据元素：人，猴子，猫咪；植物中的数据元素：树、草、花。

数据项：一个数据元素可以有若干个 数据项 组成。数据中的最小单位。

　　例：人有眼耳口鼻，也有姓名、电话、地址等。

数据对象：性质相同的数据元素的集合，数据的子集。

　　例：一群人。

本文以概括的形式，对常见的几种数据结构进行一个简单介绍，后续再做文章细化。

数组 - Array

int arr[10] = {1,2,3,4,5,67,8};

数组是在内存中连续存储的多个元素结构，在内存中分配是连续的。通过数组下标 index 访问。

优点：查询快 --> index

　　　遍历便捷

缺点：增、删慢 --> 删除 arr 中的第3位元素‘4’，那么它后面的数据都需要进行重新的 index 计算 --> 5 .3 / 67 .4 / 8 .5

　　　空间大小固定后无法扩容；一个数组中数据类型要一致；

适于 需要频繁查询、数据增删动作少，对空间要求不大的场景。

线性表 - list

线性表: 0个或多个数据元素的有限序列。

序列：线性表是一个序列，元素之间是有顺序的，第一个元素无前驱，最后一个元素无后继。其他元素均有一个前驱和后继。

有限：元素个数是有限的。

1、栈 - stack

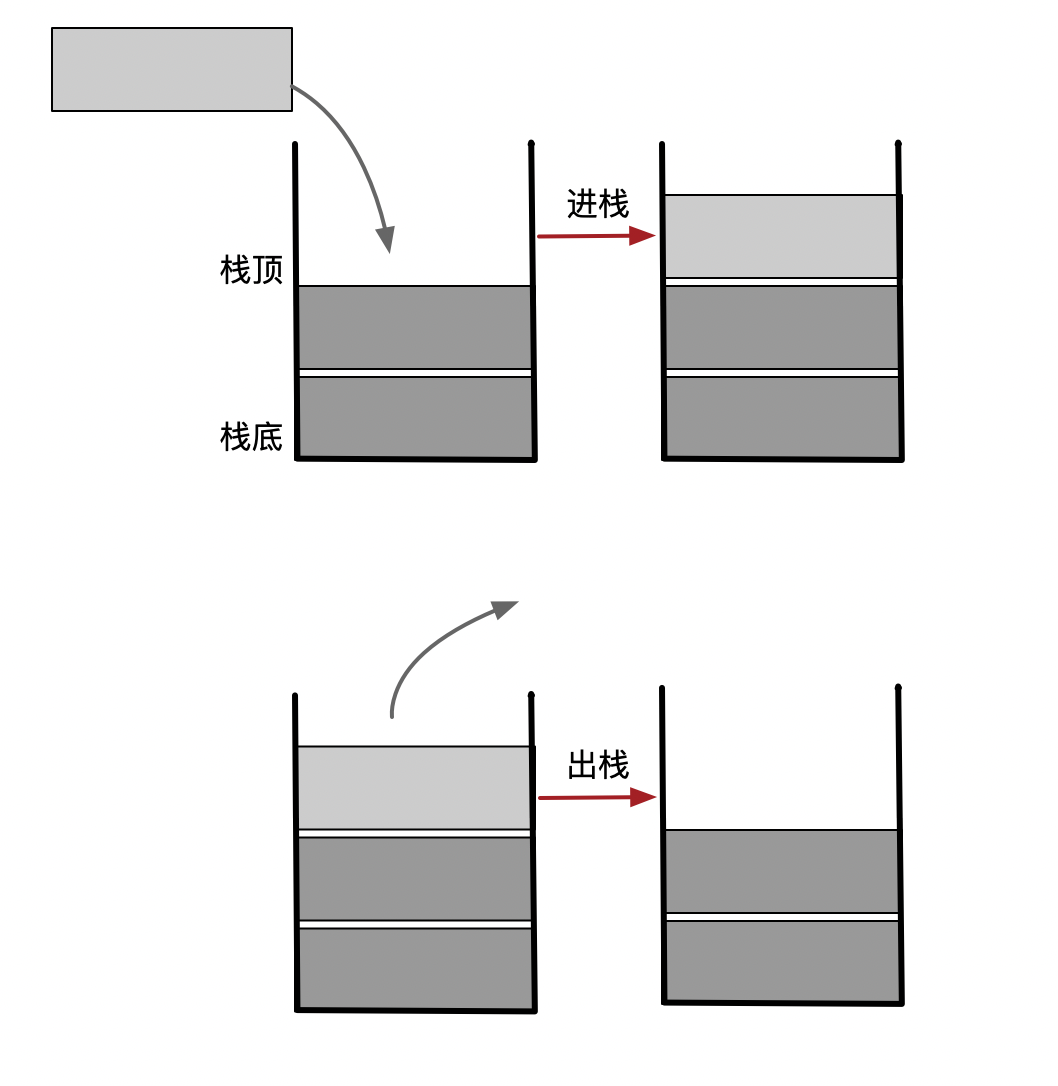
栈结构限定仅在表尾(栈顶)进行插入和删除操作的线性表。

栈结构的顺序是先进后出 FILO .

如下图，压栈出栈：

2、队列 - queue

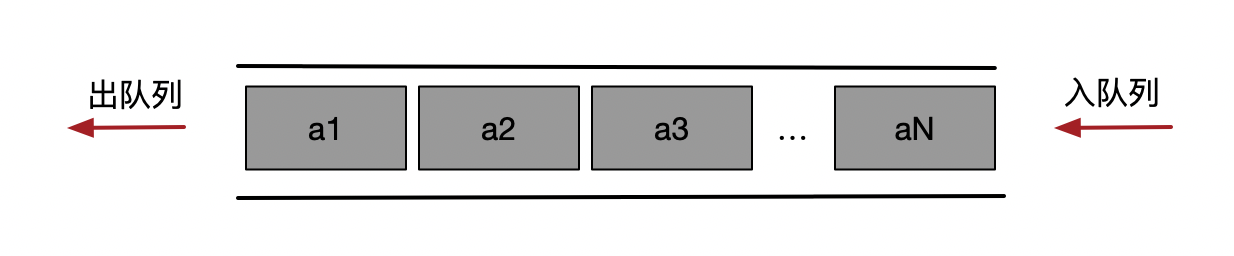
队列结构是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。 

队列是 先进先出 - FIFO 的线性表。

 

3、链表

动态的进行存储分配的一种结构，非连续、非顺序。即 链表中的个元素在内存中的地址是不连续的。链表由一系列的结点组成，结点在运行时动态生成。

结点：每个元素称为结点，它包含2部分：存储数据元素的数据域 和 存储下一个结点的地址的指针域。

根据指针的指向，链表分为：单链表、双向链表、循环列表等。

无头结点的单链表：

 头指针：链表指向第一个节点的指针，若链表有头结点，则是指向头结点的指针。

　　　　头指针具有标识作用，常用头指针表示链表的名字。

　　　　头指针是链表的必要元素。必须要有且头指针不为空。

头结点：不是链表必要的元素，可以没有。头结点是为了操作统一和方便设立的，放在第一个元素的节点之前，它的数据域一般无意义(也可以用它存放链表的长度)。

线性链表的最后一个结点指针为空，通常用 NULL 或 ^ 表示。

链表的删除：

 

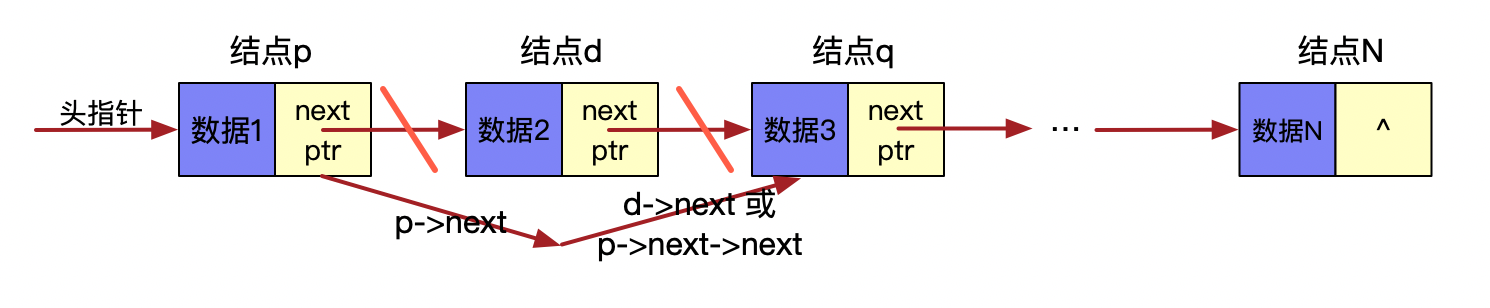
链表的增加：

 

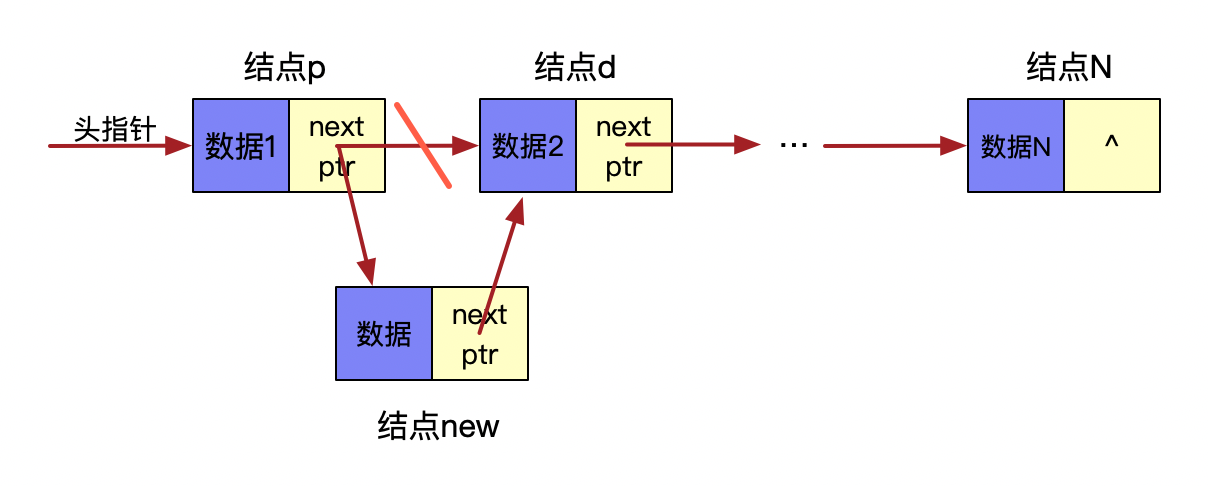
双向链表：

双链表的每个节点中有2个指针，分别指向直接后继和直接前驱。双向链表中的任一结点开始，都可以方便的访问它的前驱结点和后继结点。

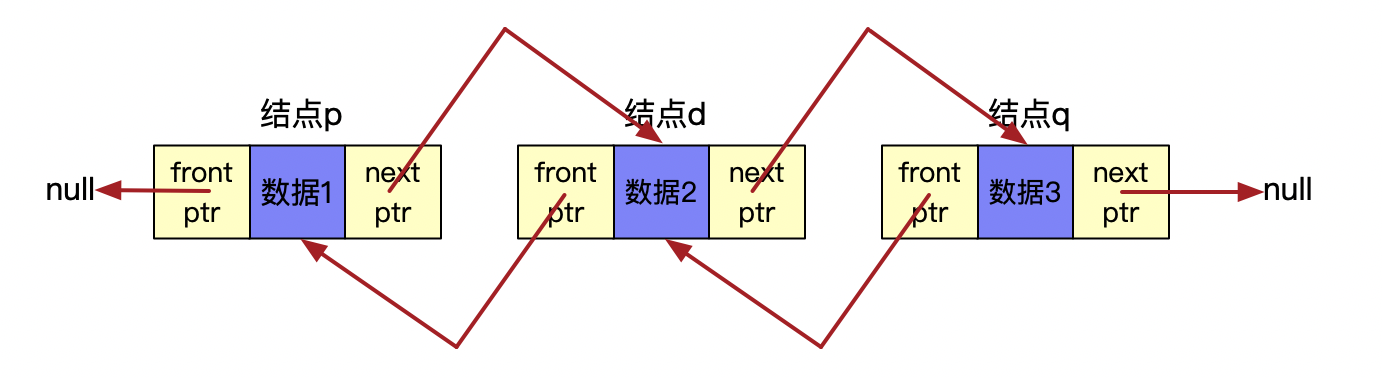
双向循环链表：

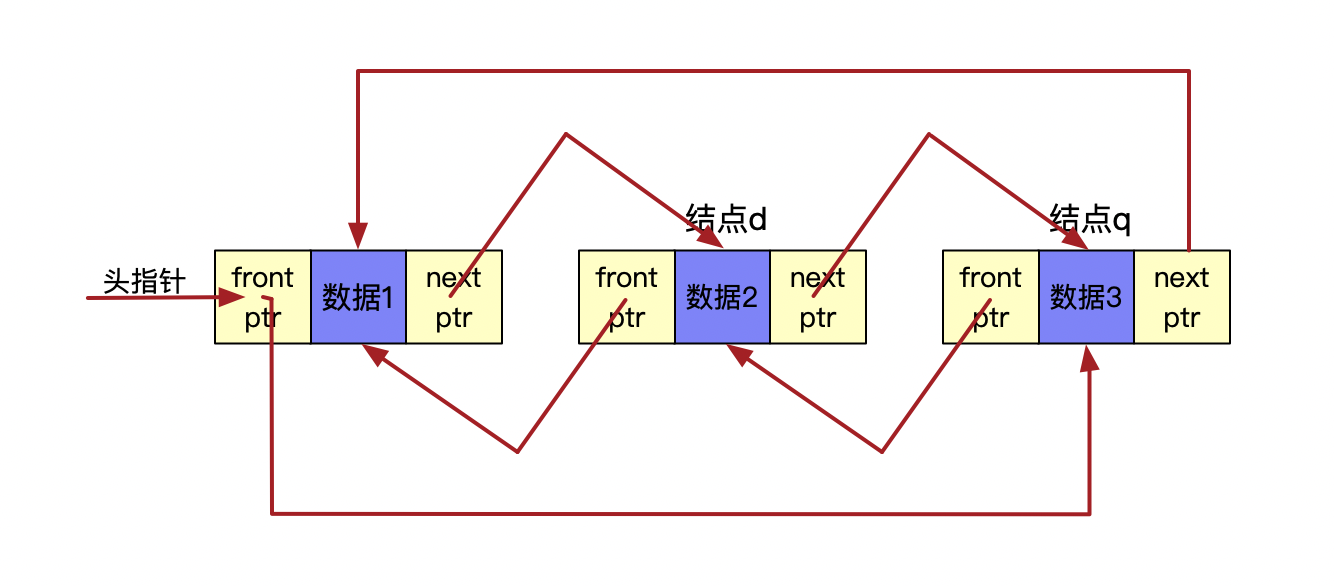
链表优点：不需要初始化容量大小，增删元素方便快速。 

缺点：占据空间比较大，因为含有大量指针域；

　　　查找很不方便，要遍历链表，很耗时。 

适于数据量小，需要频繁增删的场景。

iOS 中典型场景：AutoRealsePool . 

数结构 - Tree

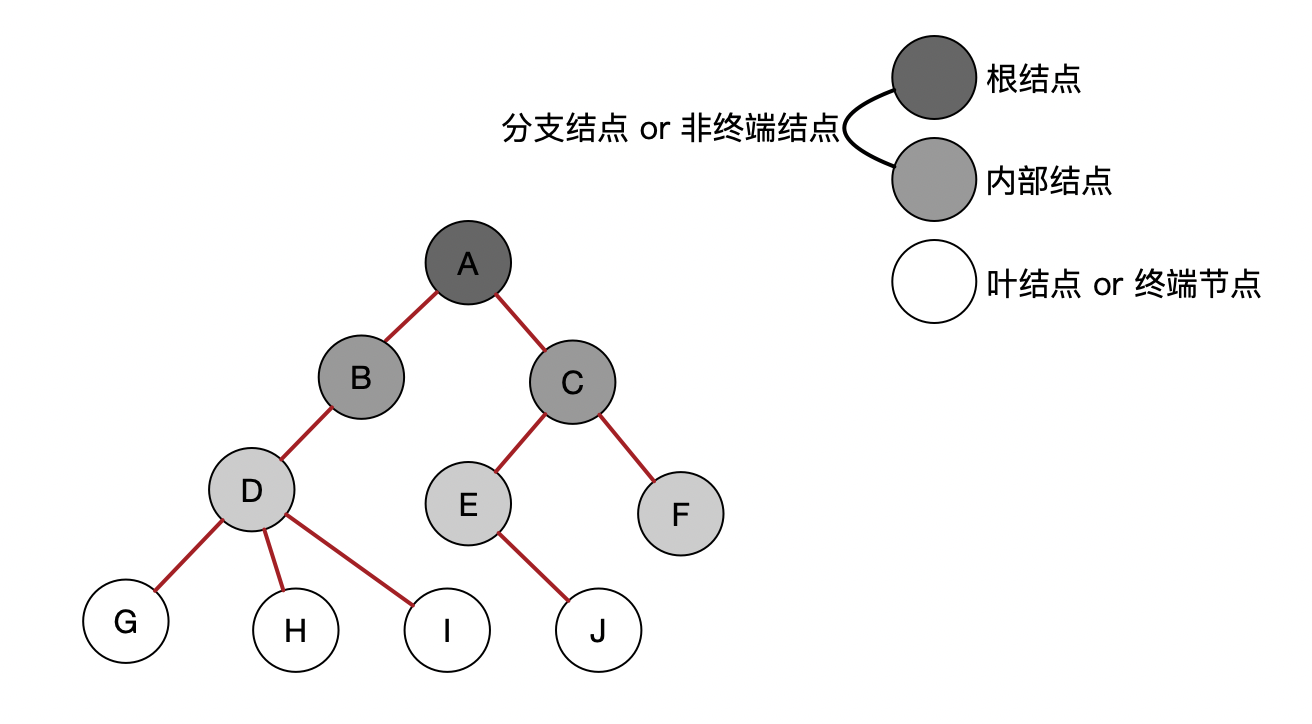
树结构由 n(n>=0) 个有限结点组成的一个具有层次关系的集合。n=0时为空树。

特点：

• 每个结点有0个或多个子结点
• 没有父结点的结点称为根节点(Root)
• 每个结点只有一个父节点(非根结点)
• 除了根结点外，每个子节点又分为多个不相交的子树(subTree)

 

1、二叉树 - Binary Tree

二叉树特点：

• 每个结点最多有2颗子树。二叉树中不存在 度 >2 的结点
• 左子树和右子树是有顺序的，次序不能颠倒
• 即使一棵树的某结点只有一个子树，也要区分它是左/右子树

二叉树的5中基本形态：

• 空二叉树
• 只有一个根结点
• 根结点只有左子树
• 根结点只有右子树
• 根结点拥有左右子树

二叉树示例：

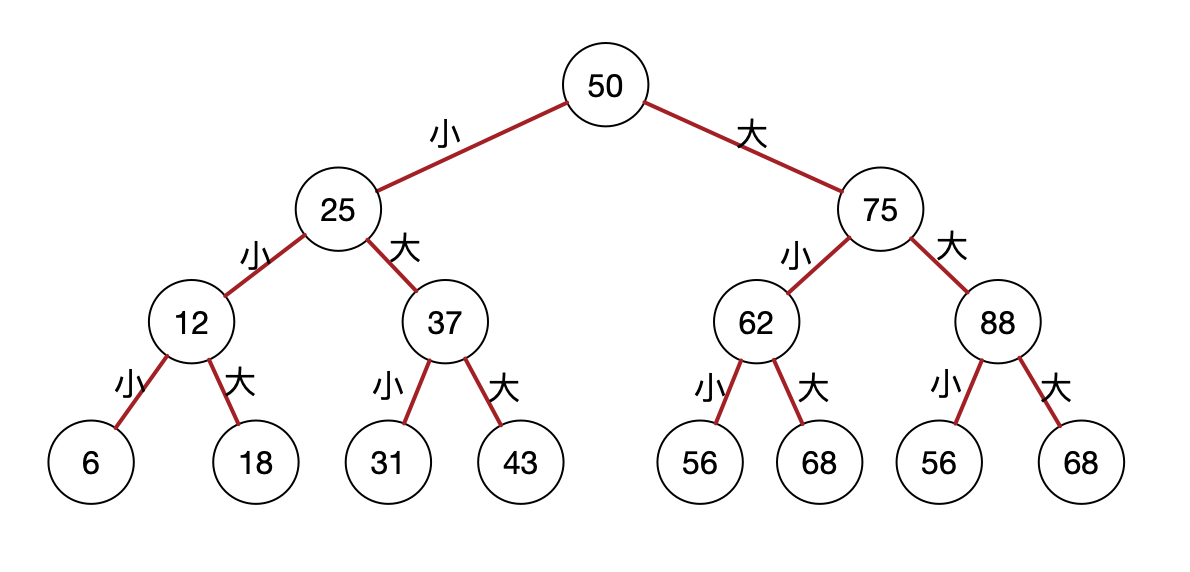
优点：

二叉树是一种比较有用的择中方案，它添加删除元素都很快，且在查找方面也有很多的算法优化，所以：

二叉树既有链表的优点，又有数组的优点，是2者的优化方案。

在处理大批量的动态数据方面非常有用。

散列表(哈希表)

散列表是根据 关键字 和 值 (key value) 直接进行访问的数据结构。通过 key 和 value 映射到集合中的一个位置，然后可快速找到集合中对应的元素。

散列技术是在记录的存储位置和他的关键字之间建立一个确定的对应关系 f，使得每个关键字 key 对应一个存储位置 f(key)。查找时，根据这个确定的对应关系找到给定值 key 的映射 f(key) ，若查找的记录存在，则就必定在 f(key) 这个位置上。

计算: 存储位置 =  f(key) :

散列函数：又称 hash 函数，用它来计算出 index 的算法函数。即 把 key 通过这个 hash 函数，转换成一个整形数字，然后将其计算结果作为数组的 index，对应的数据存储在 index 的位置。 

散列函数的要求：

• 计算简单
• 散列地址分布均匀

散列函数的构造方法：

• 直接地址法
• 数字分析法
• 平方取中法
• 折叠法
• 取余法
• 随机数法

1、直接地址法：

例：对 0~100 岁人口数字统计如下表。

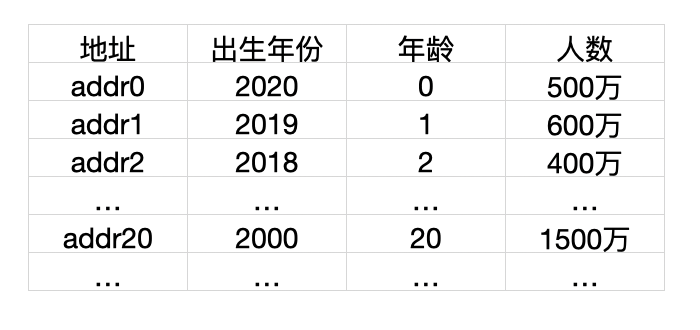
我们要某个年龄的人口数，可以对年龄这个关键字就可以直接用它的数字来作为地址 --> f(key) = key.

如果我们要计算某年出生的人口数，则可以以年份为关键字 --> f(key) = key - 2000.

这种散列函数

优点：简单、均匀，也不会产生冲突，但它需要我们事先知道关键字的分布情况。

　　　适于查找数据量小且比较连续的情况。

但实际应用中此场景很少。

2、平方取中法

例：一些数字 14 25 31 19 10 ...

平方： 196 625 961 361 100

取中：9 2 6 6 0

我们可看到有2个6，即哈希冲突。这里只介绍构造散列函数方法，后面再介绍哈希冲突。

3、取余法

简单代码示例

MyPerson： 

// .h
@interface MyPerson : NSObject
@property (nonatomic, copy) NSString *name;
@property (nonatomic, assign) NSInteger age;
- (id)initWithName:(NSString *)name age:(NSInteger)age;
- (NSInteger)myHash;
@end
// .m
@implementation MyPerson
- (id)initWithName:(NSString *)name age:(NSInteger)age {
    if (self == [super init]) {
       
        self.age = age;
        self.name = name;
    }
    return self;
}
// 散列函数
- (NSInteger)myHash {
    return self.age%10;
}
@end

存：

- (NSMutableArray *)myHashArray {
    
    if (!_myHashArray) {
        _myHashArray = [NSMutableArray arrayWithArray:@[@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil",@"nil"]];
        
        MyPerson *p1 = [[MyPerson alloc] initWithName:@"张一" age:18];
        MyPerson *p2 = [[MyPerson alloc] initWithName:@"二" age:17];
        MyPerson *p3 = [[MyPerson alloc] initWithName:@"三" age:16];
        MyPerson *p4 = [[MyPerson alloc] initWithName:@"四" age:14];
        MyPerson *p5 = [[MyPerson alloc] initWithName:@"五" age:12];
        MyPerson *p6 = [[MyPerson alloc] initWithName:@"六" age:11];
        
        [_myHashArray setObject:p1 atIndexedSubscript:p1.myHash];
        [_myHashArray setObject:p2 atIndexedSubscript:p2.myHash];
        [_myHashArray setObject:p3 atIndexedSubscript:p3.myHash];
        [_myHashArray setObject:p4 atIndexedSubscript:p4.myHash];
        [_myHashArray setObject:p5 atIndexedSubscript:p5.myHash];
        [_myHashArray setObject:p6 atIndexedSubscript:p6.myHash];

    }
    return _myHashArray;
}

想知道18岁的人的名字：

 MyPerson *p = self.myHashArray[[self hash:a]];
 NSLog(@"%ld %@",p.age,p.name);
//  18 张三

 

哈希表是基于数组衍生出的数据结构，查找直接通过 index 非常快速。但在增删元素时是比较慢的，所以很多时候需要用到一种数组链表，也就是拉链法。拉链法是一种数组结合链表的结构。

 

待续...