并行算法的设计

并行算法的设计基础

并行算法的定义和分类

• 并行算法：一些可同时执行的诸进程的集合，这些进程互相作用和协调动作从而达到给定问题的求解。

并行算法分类

• 数值计算与非数值计算
• 同步算法和异步算法
• 分布算法
• 确定算法和随机算法

并行算法的表达

描述语言

• 可以使用类Algol、类Pascal等。
• 在描述语言中引入并行语句。

并行算法的复杂性度量

串行算法的复杂性度量

• 最坏情况下的复杂度（Worst-CASE Complexity）
• 期望复杂度（Expected Complexity）

并行算法的复杂性度量

• 运行时间t(n)：包含计算时间和通信时间，分别用计算时间步和选路时间步作单位。n为问题实例的输入规模。
• 处理器数p(n)
• 并行算法成本c(n)：c(n)=t(n)p(n)
• 总运算量W(n)：并行算法求解问题时所完成的总的操作步数。

Brent定理

　　令W(n)是某并行算法A在运行时间T(n)内所执行的运算量，则A使用p台处理器可在t(n)=O(W(n)/p+T(n))时间内执行完毕。

• W(n)和c(n)密切相关
• P=O(W(n)/T(n))时，W(n)和c(n)两者是渐进一致的
• 对于任意的p，c(n)>W(n)

并行算法中的同步和通讯

同步

• 同步是在时间上强使各执行进程在某一点必须互相等待
• 可用软件、硬件和固件的方法来实现

通讯

• 共享存储多处理器使用：global read(X,Y)和global write(X,Y)
• 分布存储多计算机使用：send(X,i)和receive(Y,j)

并行计算模型

PRAM模型

PRAM（Parallel Random Access Machine）模型是多指令流多数据流（MIMD）并行机中的一种具有共享存储的模型。

基本概念

• 由Fortune和Wyllie于1978年提出，又称SIMD-SM模型。有一个集中的共享存储器和一个指令控制器，通过SM（流多处理器）的R/W交换数据，隐式同步计算。

结构图

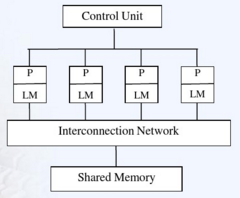
分类

(1)PRAM-CRCW并发度并发写

• CPRAM-CRCW(Common PRAM-CRCW)：仅允许写入相同数据
• PPRAM-CRCW(Priority PRAM-CRCW)：仅允许优先级最高的处理器写入
• APRAM-CRCW(Arbitrary PRAM-CRCW)：允许任意处理器自由写入

(2)PRAM-CREW并发读互斥写

(3)PRAM-EREW互斥读互斥写

计算能力比较

• PRAM-CRCW是最强的计算模型，PRAM-EREW可logp倍模拟PRAM-CREW和PRAM-CRCW

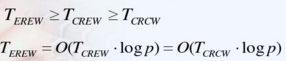
优缺点

•  适合并行算法表示和复杂性分析，易于使用，隐藏了并行机的通讯、同步等细节

• 不适合MIMD并行机，忽略了SM的竞争、通讯延迟等因素。

异步APRAM模型

基本概念

• 又称分相（Phase）PRAM或MIMD-SM。每个处理器有其局部存储器、局部时钟、局部程序；无全局时钟，各处理器异步执行；处理器通过SM进行通讯；处理器间依赖关系，需在并行程序中显式地加入同步路障。

指令类型

1. 全局读
2. 全局写
3. 局部操作
4. 同步

计算过程

由同步障分开全局相组成

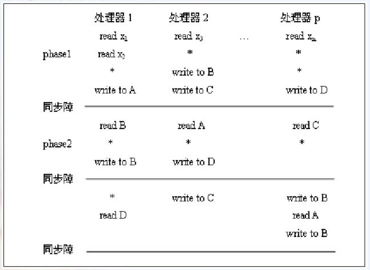
计算时间

• 设局部操作位单位时间；全局读/写平均时间为d，d随着处理器数目的增加而增加；同步路障时间为B=B(p)非降函数。
• 满足关系2≤d≤B≤p；B=B(n)=O(dlogp)或O(dlogp/logd)令t_ph为全局相内各处理器执行时间最长者，则APRAM上的计算时间为：T=∑t_ph+B×同步障次数

优缺点

• 易编程和分析算法的复杂度。
• 但与现实相差较远，其上并行算法非常有限，也不适合MIMD-DM模型。

BSP模型

基本概念

　　由Valiant（1990）提出的，“块”同步模型，是一种异步MIMD-DM模型，支持消息传递系统，块内异步并行，块间显式同步。

模型参数

• p：处理器数（带有存储器）
• l：同步障时间（Barrier synchronization time）
• g：带宽因子（time steps/packet）=1/bandwidth

计算过程

　　由若干超级步组成，每个超级步计算模式为下图：

优缺点

• 强调了计算和通讯的分离，提供了一个编程环境，易于程序复杂性分析。
• 但是需要显式同步机制，限制至多h条消息的传递等。

logP模型

基本概念

　　由Culler（1993）年提出的，是一种分布存储的、点到点通讯的多处理机模型，其中通讯由一组参数描述，实行隐式同步。

模型参数

• l：network latency
• o：communication overhead
• g：gap=1/bandwidth
• P：#processors

注：l和g反映了通讯网络的容量

优缺点

• 捕捉了MPC的通讯瓶颈，隐藏了并行机的网络拓扑、路由、协议，可以应用到共享存储、消息传递、数据并行的编程模型中。
• 但难以进行算法描述、设计和分析。

BSP vs. logP

• BSP→logP：BSP块同步→BSP子集同步→BSP进程对同步=logP
• BSP可以常数因子模拟logP，logP可以对数因子模拟BSP
• BSP=logP+Barriers-Overhead
• BSP提供了更方便的程设环境，logP更好地利用了机器资源
• BSP似乎更简单、方便和符合结构化编程

并行算法的一般设计方法

串行算法的直接并行化

算法设计方法描述

方法描述

• 发掘和利用现有串行算法中的并行性，直接将串行算法改造为并行算法。

评注

• 由串行算法直接并行化的方法是并行算法设计的最常用方法之一
• 不是所有的串行算法都可以直接并行化的
• 一个好的串行算法并不能并行化为一个好的并行算法
• 许多数值串行算法可以并行化为有效的数值并行算法

例：快排序算法的并行化

算法：PRAM-CRCW上的快排序二叉树构造算法

输入：序列（A1,...,An）和n个处理器

输出：供排序用的一颗二叉排序数

从问题描述开始设计并行算法

方法描述

• 从问题本身描述出发，不考虑相应的串行算法，设计一个全新的并行算法。

评注

• 挖掘问题的固有特性与并行的关系
• 设计全新的并行算法是一个挑战性和创造性的工作
• 利用串的周期性的PRAM-CRCW算法是一个很好的范例

借用已有的算法求解新问题

方法描述

• 找出求解问题和某个已解决问题之间的联系
• 改造或利用已知算法应用到求解问题上

评注

• 这是一项创造性的工作
• 使用矩阵乘法算法求解所有点对间最短路径是一个很好的范例

利用矩阵乘法求所有点对间最短路径

计算原理

并行算法的基本设计技术

划分设计技术

• 均匀划分技术
• 方根划分技术
• 对数划分技术
• 功能划分技术

分治设计技术

并行分治设计步骤

• 将输入划分成若干个规模相等的子问题
• 同时（并行地）递归求解这些子问题
• 并行地归并子问题的解，直至得到原问题的解

双调归并网络

平衡数设计技术

设计思想

• 以树的叶节点为输入，中间节点为处理节点，由叶向根或由根向叶逐层进行并行处理。

倍增设计技术

设计思想

• 又称指针跳跃（pointer jumping）技术，特别适合于处理链表或有向树之类的数据结构
• 当递归调用时，所要处理数据之间的距离逐步加倍，经过k步后即可完成距离为2^k的所有数据的计算

流水线设计技术

设计思想

• 将算法流程划分成p个前后衔接的任务片段，每个任务片段的输出作为下一个任务片段的输入
• 所有任务片段按同样的速率产生出结果

评注

• 流水线技术是一种广泛应用在并行处理中的技术
• 脉动算法（Systolic algorithm）是其中一种流水线技术

并行算法的一般设计过程

PCAM设计方法学

设计并行算法的四个阶段：

• 划分（Partitioning）：分解成小的任务，开拓并发性
• 通讯（Communication）：确定诸任务间的数据交换，监测划分的合理性
• 组合（Agglomeration）：依据任务的局部性，组合成更大的任务
• 映射（Mapping）：将每个任务分配到处理器上，提高算法的性能

PCAM设计过程

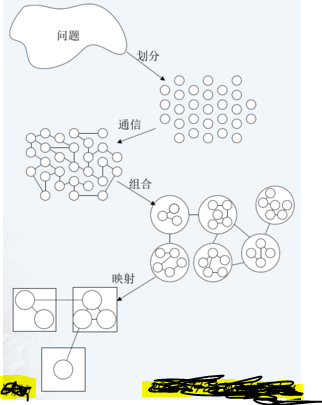
划分

划分的方法描述

• 充分开拓算法的并发性和可扩展性
• 先进行数据分解（称域分解），再进行计算功能的分解（称功能分解）
• 使数据集和计算集互不相交
• 划分阶段忽略处理器数目和目标机器的体系结构
• 能分为两类划分：①域分解（domain decomposition）；②功能分解（functional decomposition）

域分解

• 划分的对象是数据，可以是算法的输入数据、中间处理数据和输出数据
• 将数据分解成大致相等的小数据片
• 划分时考虑数据上的相应操作
• 如果一个任务需要别的任务中的数据，则会产生任务间的通讯

功能分解

• 划分的对象是计算，将计算划分为不同的任务，其出发点不同于域分解
• 划分后，研究不同任务所需的数据。如果这些数据不相交的，则划分是成功的；如果数据有相当的重叠，意味着要重新进行域分解和功能分解
• 功能分解是一种更深层次的分解

划分依据

• 划分是否具有灵活性？
• 划分是否避免了冗余计算和存储？
• 划分任务尺寸是否大致相当？
• 任务数与问题尺寸是否成比例？
• 功能分解是一种更深层次的分解，是否合理？

通讯

通讯方法描述

• 通讯是PCAM设计过程的重要阶段
• 划分产生的诸任务，一般不能完全独立执行，需要在任务间进行数据交流；从而产生了通讯
• 功能分解确定了诸任务之间的数据流
• 诸任务是并发执行的，通讯则限制了这种并发性

四种通讯模式

• 局部/全局通讯
• 结构化/非结构化通讯
• 静态/动态通讯
• 同步/异步通讯

通讯判据

• 所有任务是否执行大致相当的通讯？
• 是否尽可能的局部通讯？
• 通讯操作是否能并行执行？
• 同步任务的计算能否并行执行？

组合

方法描述

• 组合是由抽象到具体的过程，是将组合的任务能在一类并行机上有效的执行
• 合并小尺寸任务，减少任务数。如果任务数恰好等于处理器数，则也完成了映射过程
• 通过增加任务的粒度和重复计算，可以减少通讯成本
• 保持映射和扩展的灵活性，降低软件工程成本

表面-容积效应

• 通讯量与任务子集的表面成正比，计算量与任务子集的体积成正比
• 增加重复计算有可能减少通讯量

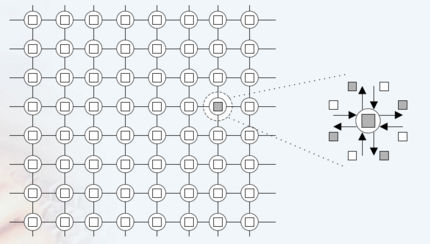
重复计算

• 重复计算减少通讯量，但增加了计算量，应保持恰当的平衡
• 重复计算的目标应减少算法的总运算时间

组合判据

• 增加粒度是否减少了通讯成本？
• 重复计算是否已权衡了其得益？
• 是否保持了灵活性和可扩展性？
• 组合的任务数是否与问题尺寸成比例？
• 是否保持了类似的计算和通讯？
• 有没有减少并行执行的机会？

映射

方法描述

• 每个任务要映射到具体的处理器，定位到运行机器上
• 任务数大于处理器数时，存在负载平衡和任务调度问题
• 映射的目标：减少算法的执行时间（并行的任务→不同的处理器；任务之间存在高通讯的→同一处理器）
• 映射实际是一种权衡，属于NP完全问题

负载平衡算法

• 静态的：事先确定
• 概率的：随机确定
• 动态的：执行期间动态负载
• 基于域分解的：递归对剖；局部算法；概率方法；循环映射

任务调度算法

• 任务放在集中的或分散的任务池中，使用任务调度算法将池中的任务分配给特定的处理器

映射判据

• 采用集中式负载平衡方案，是否存在通讯瓶颈？
• 采用动态负载平衡方案，调度策略的成本如何？

 

参考文献

https://wenku.baidu.com/view/b183017a1ed9ad51f01df2d7.html?rec_flag=default&sxts=1542421861193

 https://wenku.baidu.com/view/17709aca3186bceb19e8bbd4.html?rec_flag=default&sxts=1542421875283

https://wenku.baidu.com/view/b994bbf6998fcc22bcd10dd7.html?rec_flag=default&sxts=1542421883056