计数过程
在(0,t)内出现事件A的总数所组成的过程{N(t),t>0}称为计数过程。
如果用N(t)表示到时刻t为止已发生的“事件A”的总数,若N(t)满足下列条件:
- N(t)≥0
- N(t)取正整数值
- 对任意两个时刻t1<t2,有N(t1)≤N(t2)
- 对任意两个时刻t1<t2,N(t2)-N(t1)等于在区间(t1,t2]中发生的“事件A”的次数
则随机过程{N(t),t≥0}称为一个计数过程。
注意:
- 如果在不相交的时间区间中发生的事件个数是独立的,则称计数过程有独立增量。
- 若在任一时间区间中发生的事件个数的分布只依赖于时间区间的长度,则称计数过程有平稳增量。
独立增量过程
如果在不相交的时间间隔内出现事件A的次数是互相统计独立的则A事件的计数过程为独立增量过程。
平稳(齐次)增量计数过程
在时间间隔(t,t+s)内出现事件A的次数[N(t+s)-N(t)]仅与s有关而与t无关,则称N(t)为平稳增量计数过程。
泊松过程
设随机过程{X(t),t≥0}是一个计数过程,满足
- X(0)=0
- X(t)是独立增量过程
- 对任一长度为t的区间中事件的个数服从参数为λt(λ>0)的泊松分布,即对一切s,t≥0,有P{X(t+s)-X(s)=k}=(λt)k/(k!).exp(-λt)(其中k=0,1,2,…)
则称X(t)为具有参数λ的泊松过程。
注意:
- 从条件3可知泊松过程有平稳增量,且E[X(t)]=λt并称λ为此过程的生起率或强度(单位时间内发生事件的平均个数)。
说明:
要确定计数过程是泊松过程,必须证明它满足三个条件:
- 条件1只是说明事件的计数是从时刻t=0开始
- 条件2通常可从对过程的了解的情况去直接验证
- 然而全然不清楚如何去确定条件3是否满足
为此给出一个与泊松过程等价的定义
定义
设随机过程{X(t),t≥0}是一个计数过程,参数为λ(λ>0),满足
- X(0)=0
- X(t)是独立平稳增量过程
- X(t)满足下列两式:①P{X(t+h)-X(t)=1}=λh+o(h);②P{X(t+h)-X(t)≥2}=o(h);其中o(h)表示当h→0时对h的高阶无穷小
则称X(t)为具有参数λ的泊松过程。
泊松过程的特点
- 增量平稳性:在时间或者空间上的均匀性。
- 增量的独立性:未来的变化与过去的变化没有关系。
泊松过程为满足下列假设的计数过程
- 从t=0起开始观察事件,即N(0)=0;
- 该过程是独立增量过程;
- 该过程为平稳增量过程;
- 在(t,t+Δt)内出现一个事件的概率为λΔt+o(Δt)(当Δt→0时),λ为一常数;在(t,t+Δt)内出现事件二次以及二次以上的概率为o(Δt),即P{N(t+Δt)-N(t)≥2}=o(Δt);
泊松过程的分布特征
齐次泊松过程的递推微分方程
- P0(t+Δt))=P0(t)(1-λΔt)+O(Δt)
- Pn(t+Δt))=Pn(t)(1-λΔt)+Pn-1(t)Δt+O(Δt),k≥1
其中
- Pn(t)=Pr[N(t)-N(0)=n]
- d(P0(t))/dt=-λP0(t)
- d(Pn(t))/dt=-λPn(t)+λPn-1(t)
方程的解
- P0(t)=exp(-λt)
- P1(t)=λt.exp(-λt)
- P{N(t0+t)-N(t0)=n}=Pn=(λt)n/(n!).exp(-λt)
泊松分布的母函数
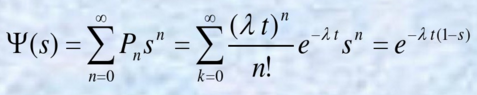
非齐次泊松过程
设有一随机的计数过程{N(t),t≥0}满足下列假设:
- N(0)=0
- {N(t),t≥0}是一独立增量过程
- P{[N(t+Δt)-N(t)]≥2}=o(Δt)
- P{[N(t+Δt)-N(t)]=1}=λ(t)Δt+o(Δt)
则称它为非齐次泊松过程。
复合泊松过程
设有泊松过程{N(t),t≥0}和一族独立同分布随机变量{Yn},n=1,2,3,...,且{N(t)}和{Yn}也是相互统计独立的。设随机过程
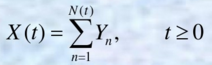
则称{X(t)}是复合泊松过程。
泊松过程的基本性质




进步是留给时间最美的礼物



