最短路径算法——Dijkstra算法与Floyd算法

转自：https://www.cnblogs.com/smile233/p/8303673.html

最短路径

　　①在非网图中，最短路径是指两顶点之间经历的边数最少的路径。

 

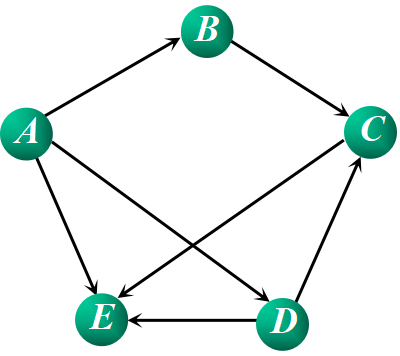
AE：1    ADE：2   ADCE：3   ABCE：3

　　②在网图中，最短路径是指两顶点之间经历的边上权值之和最短的路径。 

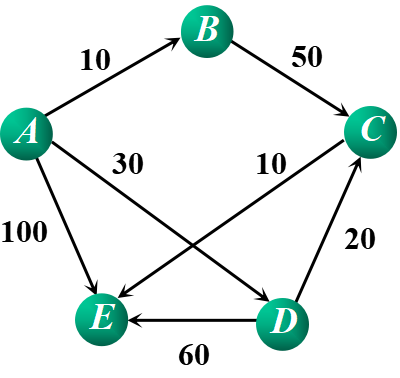
AE：100   ADE：90   ADCE：60   ABCE：70

　　③单源点最短路径问题

　　问题描述：给定带权有向图G＝(V, E)和源点v∈V，求从v到G中其余各顶点的最短路径。

　　应用实例——计算机网络传输的问题：怎样找到一种最经济的方式，从一台计算机向网上所有其它计算机发送一条消息。

　　④每一对顶点之间的最短路径

　　问题描述：给定带权有向图G＝(V, E)，对任意顶点v_i,v_j∈V（i≠j），求顶点v_i到顶点v_j的最短路径。

• 解决办法1：每次以一个顶点为源点，调用Dijkstra算法n次。显然，时间复杂度为O(n³)。
• 解决办法2：弗洛伊德提出的求每一对顶点之间的最短路径算法——Floyd算法，其时间复杂度也是O(n³)，但形式上要简单些。

Dijkstra算法

　　①基本思想：设置一个集合S存放已经找到最短路径的顶点，S的初始状态只包含源点v，对v_i∈V-S，假设从源点v到v_i的有向边为最短路径。以后每求得一条最短路径v, …, v_k，就将v_k加入集合S中，并将路径v, …, v_k , v_i与原来的假设相比较，取路径长度较小者为最短路径。重复上述过程，直到集合V中全部顶点加入到集合S中。（贪心思想）

　　②设计数据结构 :

　　1、图的存储结构：带权的邻接矩阵存储结构 。

　　2、数组dist[n]：每个分量dist[i]表示当前所找到的从始点v到终点v_i的最短路径的长度。初态为：若从v到v_i有弧，则dist[i]为弧上权值；否则置dist[i]为∞。

　　3、数组path[n]：path[i]是一个字符串，表示当前所找到的从始点v到终点v_i的最短路径。初态为：若从v到v_i有弧，则path[i]为vv_i；否则置path[i]空串。

　　4、数组s[n]：存放源点和已经生成的终点，其初态为只有一个源点v。

　　③Dijkstra算法——伪代码

1. 初始化数组dist、path和s；
2. while (s中的元素个数<n)
     2.1 在dist[n]中求最小值，其下标为k；
     2.2 输出dist[j]和path[j]；
     2.3 修改数组dist和path；
     2.4 将顶点vk添加到数组s中；

　　④C++代码实现

#include<iostream>
#include<fstream>
#include<string>
using  namespace std;
#define MaxSize  10
#define MAXCOST 10000
// 图的结构
template<class T>
struct Graph
{
    T vertex[MaxSize];// 存放图中顶点的数组
    int arc[MaxSize][MaxSize];// 存放图中边的数组
    int vertexNum, arcNum;// 图中顶点数和边数
};
// 最短路径Dijkstra算法
void Dijkstra(Graph<string> G,int v)
{
    int dist[MaxSize];//  i到j的路径长度
    string path[MaxSize];// 路径的串
    int s[MaxSize];// 已找到最短路径的点的集合
    bool Final[MaxSize];//Final[w]=1表示求得顶点V0至Vw的最短路径
    // 初始化dist\path
    for (int i = 0; i < G.vertexNum; i++)
    {
        Final[i] = false;
        dist[i] = G.arc[v][i];
        if (dist[i] != MAXCOST)
            path[i] = G.vertex[v] + G.vertex[i];
        else
            path[i] = " ";        
    }
    s[0] = v; // 初始化s
    Final[v] = true;
    int num = 1;
    while (num < G.vertexNum)
    {
        // 在dist中查找最小值元素
        int k = 0,min= MAXCOST;
        for (int i = 0; i < G.vertexNum; i++)
        {
            if (i == v)continue;
            if (!Final[i] && dist[i] < min)
            {
                k = i;
                min = dist[i];
            }                
        }
        cout << dist[k]<<path[k]<<endl;
        s[num++] = k;// 将新生成的结点加入集合s
        Final[k] = true;
        // 修改dist和path数组
        for (int i = 0; i < G.vertexNum; i++)
        {
            if (!Final[i]&&dist[i] > dist[k] + G.arc[k][i])
            {
                dist[i] = dist[k] + G.arc[k][i];
                path[i] = path[k] + G.vertex[i];
            }
        }
    }
}
int main()
{
    // 新建图
    Graph<string> G;
    string temp[]= { "v0","v1","v2","v3","v4" };
    /*int length = sizeof(temp) / sizeof(temp[0]);
    G.vertexNum = length;
    G.arcNum = 7;*/
    ifstream in("input.txt");
    in >> G.vertexNum >> G.arcNum;
    // 初始化图的顶点信息
    for (int i = 0; i < G.vertexNum; i++)
    {
        G.vertex[i] = temp[i];
    }
    //初始化图G的边权值
    for (int i =0; i <G.vertexNum; i++)
    {
        for (int j = 0; j <G.vertexNum; j++)
        {
            G.arc[i][j] = MAXCOST;
        }
    }
    for (int i = 0; i < G.arcNum; i++)
    {
        int m, n,cost;
        in >> m >> n >> cost;
        G.arc[m][n] = cost;
    }
    Dijkstra(G, 0);
    system("pause");
    return 0;
}

　　⑤测试数据

// input.txt
5 7
0 1 10
0 3 30
0 4 100
1 2 50
2 4 10
3 2 20
3 4 60

Floyd算法

　　①基本思想：对于从v_i到v_j的弧，进行n次试探：首先考虑路径v_i,v₀,v_j是否存在，如果存在，则比较v_i,v_j和v_i,v₀,v_j的路径长度，取较短者为从v_i到v_j的中间顶点的序号不大于0的最短路径。在路径上再增加一个顶点v₁，依此类推，在经过n次比较后，最后求得的必是从顶点v_i到顶点v_j的最短路径。

　　②设计数据结构

　　1、图的存储结构：带权的邻接矩阵存储结构  。

　　2、数组dist[n][n]：存放在迭代过程中求得的最短路径长度。迭代公式：

          

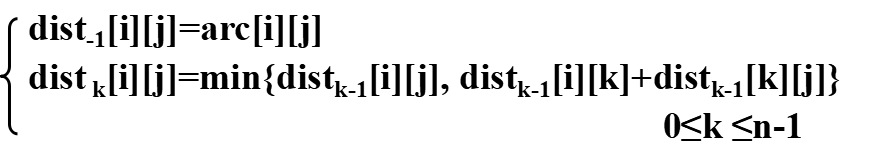
　　3、数组path[n][n]：存放从v_i到v_j的最短路径，初始为path[i][j]="v_iv_j"。

　　③C++代码实现

#include<iostream>
#include<fstream>
#include<string>
using  namespace std;
#define MaxSize  10
#define MAXCOST 10000
int dist[MaxSize][MaxSize];// 存放在迭代过程中求得的最短路径
string path[MaxSize][MaxSize];// vi到vj的最短路径
// 图的结构
template<class T>
struct Graph
{
    T vertex[MaxSize];// 存放图中顶点的数组
    int arc[MaxSize][MaxSize];// 存放图中边的数组
    int vertexNum, arcNum;// 图中顶点数和边数
};
void Floyd(Graph<string> G)
{    
    // 初始化
    for(int i=0;i<G.vertexNum;i++)
        for (int j = 0; j < G.vertexNum; j++)
        {
            if (i == j) { dist[i][j] = 0; path[i][j] = ""; }
            dist[i][j] = G.arc[i][j];
            if (dist[i][j] != MAXCOST)
                path[i][j] = G.vertex[i] + G.vertex[j];
            else
                path[i][j] = " ";
        }
    // 进行n次迭代
    for(int k=0;k<G.vertexNum;k++)
        for(int i=0;i<G.vertexNum;i++)
            for (int j = 0; j < G.vertexNum; j++)
                if (dist[i][k] + dist[k][j] < dist[i][j])
                {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    path[i][j] = path[i][k] + path[k][j];
                }            
}
int main()
{
    int i, j, cost;
    Graph<string> G;// 存放图的信息
    ifstream in("input.txt");
    in >> G.vertexNum >> G.arcNum;
    string temp[] = { "a","b","c" };    
    // 初始化图的顶点信息
    for (int i = 0; i < G.vertexNum; i++)
    {
        G.vertex[i] = temp[i];
    }
    //初始化图G
    for (i = 0; i < G.vertexNum; i++)
    {
        for (j = 0; j < G.vertexNum; j++)
        {
            G.arc[i][j] = MAXCOST;
        }
    }
    //构建图G
    for (int k = 0; k <G.arcNum; k++)
    {
        in >> i >> j >> cost;
        G.arc[i][j] = cost;
    }
    Floyd(G);
    for (i = 0; i < G.vertexNum; i++)
    {
        for (j = 0; j < G.vertexNum; j++)
        {
            if (i != j)
            {
                cout << "顶点" << i << "到顶点" << j << "的最短路径长度为" << dist[i][j] << endl;                                
                cout << "具体路径为:" << path[i][j] << endl;
            }
        }
    }
    system("pause");
    return 0;
}

　　④测试数据

// input.txt
5
1 4
0 6
2 11
0 3
2 2