博客园  :: 首页  :: 新随笔  :: 联系 :: 订阅 订阅  :: 管理

计算复杂度-几种问题及其关系

Posted on 2018-10-01 11:23  MwingFly  阅读(596)  评论(0)  编辑  收藏  举报

转自：https://blog.csdn.net/golden1314521/article/details/51470999/

几种问题及其关系

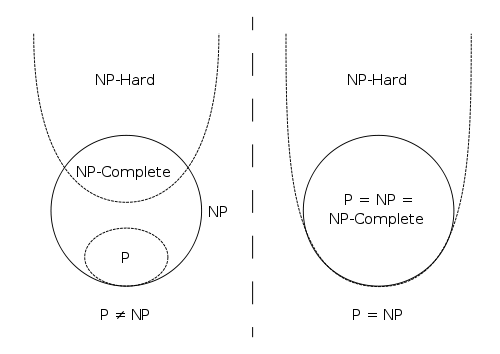
首先解释一下什么是NP问题，什么是NP hard问题，什么是NP完全问题。

  • P Problem：这个应该最易理解，就是一个问题可以在Polynominal的时间的得到解决，当然，是对于任意input size。
  • NP Problem：对于一类问题，我们可能没有一个已知的快速的方法得到问题的答案，但是如果给我们一个candidate answer，我们能够在polynominal的时间内验证这个candidate answer到底是不是我们已知问题的答案，这类问题叫做NP problem。所以很显然 P Problem是NP problem的一个子集。
  • NP-hard Problem：对于这一类问题，用一句话概括他们的特征就是“at least as hard as the hardest problems in NP Problem”， 就是NP-hard问题至少和NP问题一样难。
  • NP-Complete Problem：对于这一类问题，他们满足两个性质，一个就是在polynomial时间内可以验证一个candidate answer是不是真正的解，另一个性质就是我们可以把任何一个NP问题在polynomial的时间内把他的input转化，使之成为一个NP-complete问题（即规约）。NP-Complete Problem问题可以互相转换 (在多项式时间内)，只要其中一个问题可以在多项式时间内解决，那么其他问题也都将可以在多项式时间内解决。
    这里写图片描述

规约——一种技巧

归约（reduction）： 规约是证明NP-hard问题的一种常用方法，通常用<=<=这个符号来表示。如P<=QP<=Q，这个就表示P is reducible to Q , or Q is the reduction from P or P is reduced to Q（P问题可以归约到Q问题，or可以把P归约到Q） 。这里的reduction的符号可以当成是 比较难易程度的小于等于号，意味着P至少比Q容易，或者Q至少比P难。
归约主要做的就是以下两个转化（注意两个转化都要在polynomial的时间内完成）【已知PP 是个NP-hard问题，证新问题QQ 亦是NP-hard问题】，
1. 把P的输入转化到Q的输入；
2. 把Q的输出转化到P的输出。
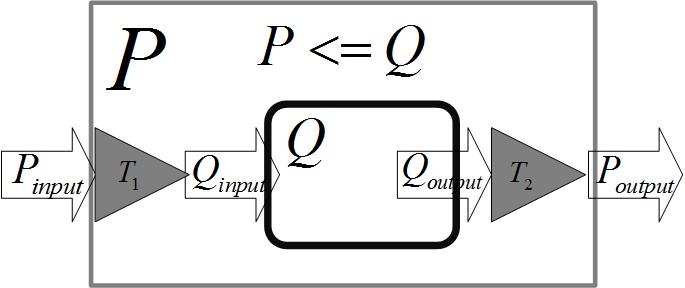
下图展示了上述规约过程。其中T1T1 在多项式时间将 P的输入PinputPinput 转化成Q的输入QinputQinput ; T2T2在多项式时间将 Q的输出QoutputQoutput 转化成P的输出PoutputPoutput 。也就是说NP-hard问题PP 可以依赖于对问题QQ 的解决而解决。那么QQ 至少比PP要难，即P<=QP<=Q。
这里写图片描述

如何对问题证明

下面来列出了一些常见的证明问题及其证明套路。

  • 证明NP问题。这个容易，即给你一个结果，你能在polynomial的时间内验证该结果的正确性。
  • 证明NP-hard问题。我们要证明一个问题是NP-hard的时候，我们通常要做的是找到一个已被证明了的NPC问题，并把这个NPC问题归约到该问题上去（即NPC<=NP-hard）。
  • 证明NP-Complete问题。分以下两步：
    1. 第一步证明这个问题属于NP；
    2. 第二步，证明这个问题是NP-hard的。

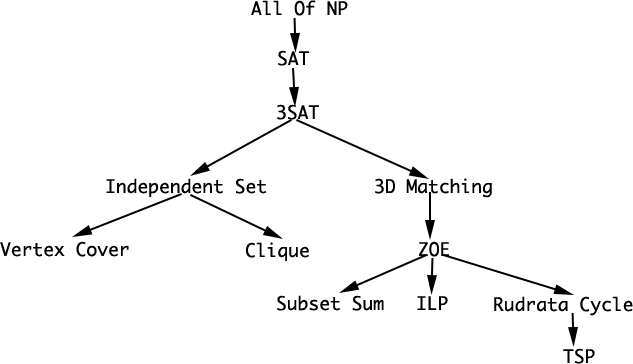
下图列出了几个已被发现NP-Complete问题（更全面的NP-Complete问题列表，见链接A compendium of NP optimization problems，以及List of NP-complete problems），及其规约关系。可以看出所有的NP问题都可以规约到SAT(即NP<=SAT)，也就是说SAT至少与NP问题一样难，或者如果解决了3SAT问题，所有的NP问题就解决了。同样的，SAT<=3SAT，3SAT<=Independent Set，Independent Set<=Vertex Cover OR Clique。

规约关系具有传递性，所以有3SAT<=Vertex Cover，NP<=NP-Complete。 事实上，由于NP-Complete⊂⊂ NP 且 NP<=NP-Complete，可以推导出 所有的NP-Complete 可以相互规约，也就是所有的NP-Complete都是等价的。
这里写图片描述

NP-Complete间的规约例子

1. 3SAT<=Independent Set

  • 在图G中若顶点集合S满足其中的任意两个顶点之间不存在边，则称S为独立集。The input of Independent Set is a graph GG and a number mm（独立集问题的两个参数：图GG以及独立集的大小mm）, the problem is to find a set of mm pairwise non-adjacent vertices(问题是找到GG的一个大小为mm的独立集).

  • 转化过程：Given an instance 3SAT problem with mm clauses, create an instance (G,m)(G,m) of Independent Set as follows:

    • Graph G has a triangle(edge or vertex) for each clause, with vertices labeled by the clause’s literals
    • Add edge between any two vertices that represent opposite literals.
    • The goal gg is set to the number of clauses.
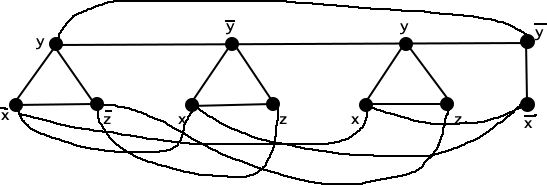
      The graph below corresponding to (x¯∨y∨z¯)∧(x∨y¯∨z)∧(x∨y∨z)∧(x¯∨y¯)(x¯∨y∨z¯)∧(x∨y¯∨z)∧(x∨y∨z)∧(x¯∨y¯) (clearly m=3m=3)
      这里写图片描述
    • 假设上图有一个最大独立集，则每个三角形中有且仅有一个顶点在该独立集中，设该顶点取值为1，其余顶点取值0，则其肯定是一个满足的3SAT的赋值。

  • 容易证明该规约过程用了多项式时间。

  • 把P的输入转化到Q的输入：P的输入是包含mm个clause的3SAT表达式；Q的输入当然是转化得到的图形GG以及独立集的大小参数g=mg=m。
  • 把Q的输出转化到P的输出：Q的输出是GG的一个大小为gg的独立集；P的输出是3SAT的一个赋值。假设GG中有一个大小为mm的独立集，则一定是1)三角形内部三个顶点只能取一个 2)不属于三角形的边所连接的顶点也只取一个。对于每个clause，如果选择了xx对应的顶点，则令x=1x=1，如果选择了x¯x¯对应的顶点，则令x¯=1x¯=1. 则该赋值是满足的。

2. 3SAT <= Vertex Cover

  • 图的顶点覆盖（有时是节点覆盖）是一组顶点的集合，使得图的每个边缘至少与集合中的一个顶点相连接。在这里Vertex Cover问题是给定图GG和点集的个数gg，要找到图GG的一个大小为gg的点覆盖。（我们常说的最小顶点覆盖的问题称为顶点覆盖问题，毫无疑问，它也是一个NP-Complete问题）。

  • 转化过程：

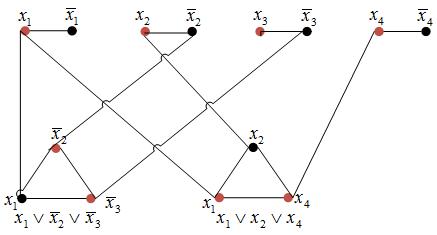
    • 按照如下方法构造Graph，对应每一个变量xixi，我们构造点二元点对 xixi和x¯ix¯i; 对于每一个clause，我们构造三角形的三个顶点，这3个点直接彼此有边，假设这三个点叫A,B,CA,B,C，我们要建立A,B,CA,B,C这三个点和该clause的联系：假设我们的clause是 (x1∨x¯2∨x¯3)(x1∨x¯2∨x¯3) 我们就把x1x1和AA连起来，x¯2x¯2和BB连起来，x¯3x¯3和CC连起来。
    • 下面的graph对应于(x1∨x¯2∨x¯3)∧(x1∨x2∨x4)(x1∨x¯2∨x¯3)∧(x1∨x2∨x4)。
      这里写图片描述
    • 若上图存在最小点覆盖，则将二元点对中在该最小点覆盖中的那一个赋值为1。则该赋值就是一个满足3-SAT的赋值。

  • 假设有mm个clause，nn个变量。则该规约过程建立了3m+2n3m+2n个点，n+3m+3mn+3m+3m个边。显然可以在多项式时间完成该转换。

  • 把P的输入转化到Q的输入：P的输入是包含mm个clause的3SAT表达式；Q的输入当然是转化得到的图形GG以及覆盖集的大小参数g=2m+ng=2m+n。
  • 把Q的输出转化到P的输出：Q的输出是GG的一个大小为g=2m+ng=2m+n的覆盖集；P的输出是3SAT的一个赋值。假设有图GG的一个大小为g=2m+ng=2m+n的顶点覆盖，则其中必定包含所有二元点对中的一个点和三角形的两个顶点。对于每个clause对应的三角形的三个边必定被至少一个点覆盖，所以有一个可满足的真值赋值；对于每个二元点对，如果xixi在SS中，则xi=1xi=1，如果x¯ix¯i在SS中，则xi=0xi=0。

3. 3SAT <= ILP

  • ILP就是Integer Linear Programming，即所有变量都要求是整数。
  • 转化过程：
    • 对于 每个clause，我们都对应于ILP中的一个constraint，比如 3SAT中有4个变量，x1x1，x2x2，x3x3 和x4x4， 则ILP中也有同样的这4个变量，并且我们要求他们都是只能取0 或 1。对于一个clause，如(x1∨x¯2∨x¯3)(x1∨x¯2∨x¯3)，我们对应的constraint是 “x1+（1−x2）+（1−x3）=1x1+（1−x2）+（1−x3）=1。很显然了，ILP中的变量选0对应于3SAT中的变量选00，ILP中的变量选1对应于3SAT中的变量选11.
    • 3SAT问题(x1∨x¯2∨x¯3)∧(x1∨x2∨x4)(x1∨x¯2∨x¯3)∧(x1∨x2∨x4)对应的ILP如下：
       
      {x1+（1−x2）+（1−x3）=1x1+x2+x4=1{x1+（1−x2）+（1−x3）=1x1+x2+x4=1
  • 至于input/output的转换，就如转换过程的描述，异常简单。在此不再叙述。

4. 3SAT <= Hamiltonian cycle problem

  • 转化过程：
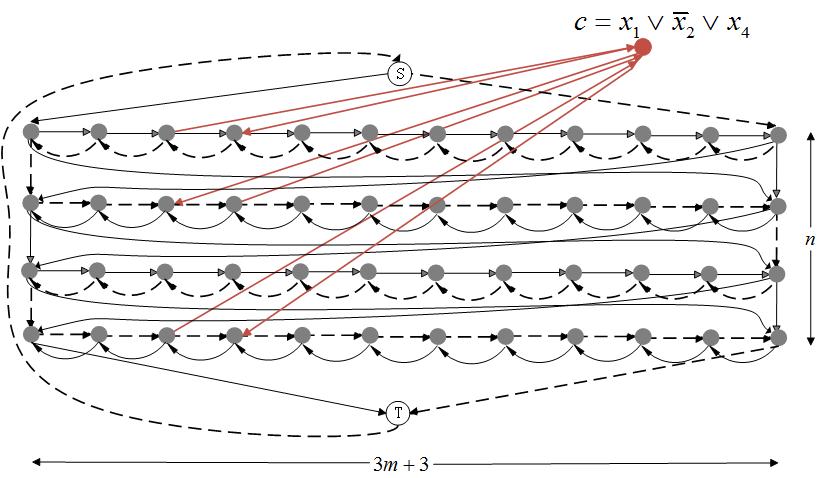
    • 对每个变量xi(1≤i≤n)xi(1≤i≤n)，创建3m+33m+3个顶点，命名为vi,1,vi,2,⋯,vi,3m+3vi,1,vi,2,⋯,vi,3m+3，并且对相邻序号的两个顶点添加互相之间的有向边。如果 xi=1xi=1，则形成从左向右的一个路径；如果 x¯i=1x¯i=1，则形成从右向左的一个路径。
    • 对每个1≤i≤n−11≤i≤n−1，添加四条有向边(vi,1,vi+1,1),(vi,3m+3,vi+1,3m+3),(vi,1,vi+1,3m+3),(vi,3m+3,vi+1,1)(vi,1,vi+1,1),(vi,3m+3,vi+1,3m+3),(vi,1,vi+1,3m+3),(vi,3m+3,vi+1,1)。
    • 添加两个节点s,ts,t，添加有向边(s,v1,1),(s,v1,3m+3),(vn,1,t),(vn,3m+3,t)(s,v1,1),(s,v1,3m+3),(vn,1,t),(vn,3m+3,t)。然后再添加有向边(t,s)(t,s)。这时得到的图中有 hamiltonian cycle，其中一个如下图的虚线所示。
    • 对于每一个clause cj=z1z2z3cj=z1z2z3，创建对应的顶点cjcj。如果z=xiz=xi，则添加有向边(vi,3j,cj)和(cj,vi,3j+1)(vi,3j,cj)和(cj,vi,3j+1); 如果z=x¯iz=x¯i，则添加有向边(cj,vi,3j)和(vi,3j+1,cj)(cj,vi,3j)和(vi,3j+1,cj)。这里1≤j≤m,1≤i≤n1≤j≤m,1≤i≤n。如对子句c=x1∨x¯2∨x4c=x1∨x¯2∨x4 生成如下图中红色所示。如果选择子句中x1=1x1=1，则x1x1对应的路径为从左向右；如果选择x¯2=1x¯2=1，则x2x2对应的路径为从右到左；如果选择x4=1x4=1，则x4x4对应的 路径为从左到右。这样我们就得到了最终的图GG。这里写图片描述
    • 若图GG有Hamiltonian cycle，则对每一个变量xixi对应的路径都是单向的，若为从左到右，则xi=1xi=1；若为从右到左，则xi=0xi=0。则该赋值肯定是3SAT可满足的。
  • 该转化过程要创建(3m+3)n+m+2(3m+3)n+m+2个点和(3m+2)×2×n+4(n−1)+5+2m(3m+2)×2×n+4(n−1)+5+2m个边，是多项式时间的。
  • 把P的输入转化到Q的输入：P的输入是包含mm个clause,nn个变量的的3SAT表达式；Q的输入当然是转化得到的包含(3m+3)n+m+2(3m+3)n+m+2个点和(3m+2)×2×n+4(n−1)+5+2m(3m+2)×2×n+4(n−1)+5+2m个边的图形GG。
  • 把Q的输出转化到P的输出：Q的输出是GG的一个Hamiltonian cycle；P的输出是3SAT的一个赋值。

5. Subset sum problem <= Partition problem

  • 问题描述：
    • Subset sum problem：given a set (or multiset) of integers T=(t1,t2,⋯,tn)T=(t1,t2,⋯,tn), is there a non-empty subset whose sum is kk。
    • Partition problem: partition problem (or number partitioning) is the task of deciding whether a given multiset WW of positive integers can be partitioned into two subsets W1W1 and W2W2 such that the sum of the numbers in W1W1 equals the sum of the numbers in W2W2.

  • 转化过程：

    • 给定一个子集和的实例为T=(t1,t2,⋯,tn)T=(t1,t2,⋯,tn)，数kk。设∑t∈Tt=A∑t∈Tt=A，则在TT的基础上添加两个数{2A−k,A+k}{2A−k,A+k}，组成一个划分问题的实例WW，即
       
      W={T,2A−k,A+k}.W={T,2A−k,A+k}.
      则∑w∈Ww=4A∑w∈Ww=4A。
    • 假设找到了WW的一个划分W1W1和W2W2，则有
       
      ∑w∈W1w=∑w∈W2w=2A。∑w∈W1w=∑w∈W2w=2A。
      而且，新添加的两个元素肯定不会同时在W1W1或W2W2里，否则二者所在的子集的元素和必定大于二者之和3A>2A3A>2A。2A−k2A−k所在的子集的其它元素就是一个满足子集和问题的子集。

  • 把P的输入转化到Q的输入：P的输入是集合TT以及数kk；Q的输入是W={T,2A−k,A+k}.W={T,2A−k,A+k}.

  • 把Q的输出转化到P的输出：Q的输出是WW的二划分W1W1和W2W2，有∑w∈W1w=∑w∈W2w∑w∈W1w=∑w∈W2w；P的输出是2A−k2A−k所在的子集的其它元素集合。

6. Clique problem<=Subgraph isomorphism problem

  • 问题描述
    • Clique problem：给定一个图G=(V,E)G=(V,E)和整数kk，找到GG的大小为kk的团。
    • Subgraph isomorphism problem：给定两个图G1=(V1,E1),G2=(V2,E2)G1=(V1,E1),G2=(V2,E2)，能否找到G1G1的一个子图HH，使得HH与G2G2同构。
  • 转换过程：
    • 令G1=GG1=G，构造G2G2为包含kk个顶点的完全图（即团）。
    • 如果子图同构问题的答案是肯定的，那么枚举GG中的任意kk个顶点并判定其是否是团，复杂度是多项式的CknCnk。
  • 把P的输入转化到Q的输入：P的输入是图G=(V,E)G=(V,E)和整数kk；Q的输入是G1G1和G2G2。
  • 把Q的输出转化到P的输出：Q的输出是Yes/No；P的输出是GG的一个团。

7. Partition problem <= Knapsack problem

  • 问题描述：
    • Partition problem： partition problem (or number partitioning) is the task of deciding whether a given multiset WW of positive integers can be partitioned into two subsets W1W1 and W2W2 such that the sum of the numbers in W1W1 equals the sum of the numbers in W2W2, i.e.
       
      ∑t∈W1t=∑t∈W2t=∑t∈Wt2.∑t∈W1t=∑t∈W2t=∑t∈Wt2.
    • Knapsack problem：Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. 给定一个物品集合U={u1,u2,⋯,un}U={u1,u2,⋯,un}，且每个物品有大小s(u)s(u)和价值w(u)w(u)，正整数BB和正数KK，是否存在子集U′⊂UU′⊂U使得
       
      ∑u∈U′s(u)≤B,∑u∈U′w(u)≥K.∑u∈U′s(u)≤B,∑u∈U′w(u)≥K.
  • 转化过程：
    • For each t∈Wt∈W，构造一个item uu 且s(u)=w(u)=ts(u)=w(u)=t, 然后对 B,KB,K添加如下条件
       
      B=K=∑u∈Uu2，B=K=∑u∈Uu2，
      那么有
       
      ∑u∈U′s(u)=∑u∈U′w(u)=∑u∈Uu2。∑u∈U′s(u)=∑u∈U′w(u)=∑u∈Uu2。

8. Vertex Cover <=Independent Set

  • 问题描述：
    • Vertex Cover：给定一个图G=(V,E)G=(V,E)和整数kk，找到GG的大小为kk的点覆盖。
    • Independent Set：给定一个图G=(V,E)G=(V,E)和整数kk， 找到GG的大小为kk的独立集。
  • 转化过程：
    • 把参数为G=(V,E)G=(V,E)和整数kk的点覆盖问题转化为参数为G=(V,E)G=(V,E)和整数|V|−k|V|−k的独立集问题。
    • 若GG中有|V|−k|V|−k大小的独立集S′S′，则GG中的任意一条边的两端点不可能都在S′S′里。也就是说，GG的任意一条边至少与该独立集S′S′之外的其余kk个顶点的某一个关联，即该独立集S′S′之外的其余kk个顶点是GG的一个大小为kk的点覆盖。
  • 把P的输入转化到Q的输入：P的输入是图G=(V,E)G=(V,E)和整数kk；Q的输入是图G=(V,E)G=(V,E)和整数|V|−k|V|−k；
  • 把Q的输出转化到P的输出：Q的输出是GG的|V|−k|V|−k大小的独立集S′S′，P的输出是V−S′V−S′.

9. Independent Set <= Clique problem

  • 问题描述：
    • Independent Set：给定一个图G=(V,E)G=(V,E)和整数kk， 找到GG的大小为kk的独立集。
    • Clique problem：给定一个图G=(V,E)G=(V,E)和整数kk，找到GG的大小为kk的团。
  • 转化过程：
    • 把GG的大小为kk的独立集问题转化为补图G¯G¯的大小为kk的团问题。
    • 如果找到补图G¯G¯的大小为kk的团，则该团内的任意两个顶点在原图GG中没有连接边，即该团的kk个顶点是原图GG的大小为kk的独立集。
  • 把P的输入转化到Q的输入：P的输入是图G=(V,E)G=(V,E)和整数kk；Q的输入是补图G¯G¯和整数kk；
  • 把Q的输出转化到P的输出：Q的输出是补图G¯G¯的kk大小的独立集S′S′，P的输出是V−S′V−S′.

10. Hamiltonian cycle problem <= Hamiltonian path problem

  • 问题描述：
    • Hamiltonian cycle problem：a graph cycle (i.e., closed loop) through a graph that visits each node exactly once
    • Hamiltonian path problem： a graph path between two vertices of a graph that visits each vertex exactly once.
  • 转化过程：
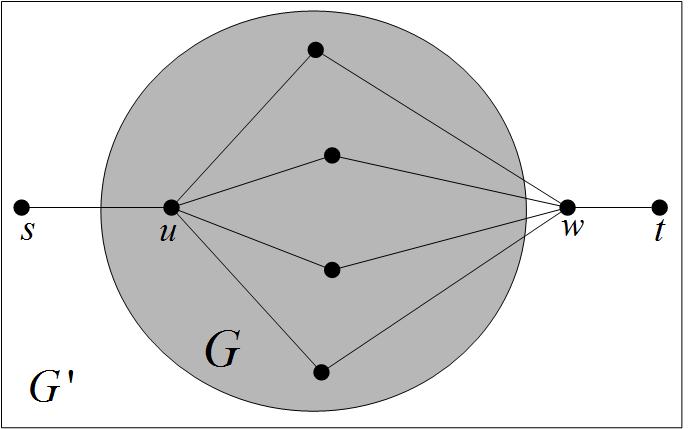
    这里写图片描述
    • 在原图GG基础上再添加s,w,ts,w,t三个顶点，任选GG中一点uu，连接(s,u),(w,t)(s,u),(w,t)以及连接uu的所有相邻节点与ww，生成新图G′G′。如上图所示。
    • 假设新图G′G′有一个Hamiltonian path <s,u,v1,v2,⋯,v,w,t><s,u,v1,v2,⋯,v,w,t>，由于u,vu,v为相邻节点，故<u,v1,v2,⋯,v><u,v1,v2,⋯,v>为GG的Hamiltonian cycle。

11. Hamiltonian cycle problem <= Traveling salesman problem

  • 问题描述：
    • Hamiltonian cycle problem：a graph cycle (i.e., closed loop) through a graph G=(V,E)G=(V,E) that visits each node exactly once。
    • Traveling salesman problem： 即给定一个带权图G′=(V′,E′)G′=(V′,E′)和数kk，找到一个费用为kk的回路。
  • 转化过程：如何得到G′=(V′,E′)G′=(V′,E′)和数kk
    • V’=V，k=0..
    • E’为完全图的边。还要定义边的权重：
       
      w(u,v)={0,if(u,v)∈E1,if(u,v)∉Ew(u,v)={0,if(u,v)∈E1,if(u,v)∉E
    • 如果G′=(V′,E′)G′=(V′,E′)有个费用为k=0k=0的回路，则说明这些边都是在GG中存在的，因此是GG的一个Hamiltonian cycle problem。

参考资料