题解 Bear and Bowling 4

题目链接

先将题目进行抽象（此处省去一定的数学分析），有以下式子：

设 \(S(i)=\sum_{j=1}^{i}j\times a_j\) ，及 \(S2(i)=\sum_{j=1}^{i}a_j\)

那么一段区间 \([l,r]\) 的贡献计算即：

\[S(r)-S(l-1)-(l-1)\times [S2(r)-S2(l-1)] \]

不妨每次固定右端点 \(r\)，即将右端点看做 \(i\)，尝试求出最优的左端点，这里为了方便，可以将 \(l-1\) 看做 \(j\)，那么满足 \(j\in [0,i)\)。

那么式子改写为：

\[dp_i=\max\{S_i-S_j-j\times (S2_i-S2_j)\} \]

不难发现式子中有 \(j\times S2_i\) 这种 \(i,j\) 乘积项，所以考虑斜率优化。

首先将 \(\max\) 拆开，并做一定恒等变形，可得：

\[(j\times S2_j-S_j)=(S2_i\times j)+(dp_i-S_i) \]

这里依次对应 \(y=kx+b\)，即 \(y=j\times S2_j-S_j\)，\(k=S2_i\)，\(x=j\)，\(b=dp_i-S_i\)。

我们期望让 \(dp_i\) 最大，即期望让截距最大。所以维护上凸壳（这里维护凸壳拐点，即 \((j,j\times S2_j-S_j)\)），即斜率递减。

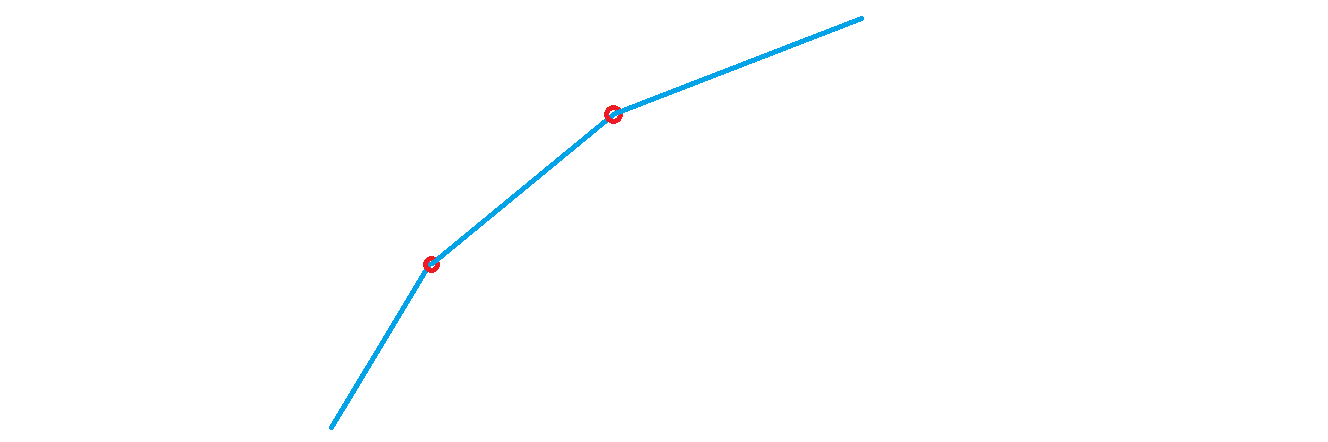
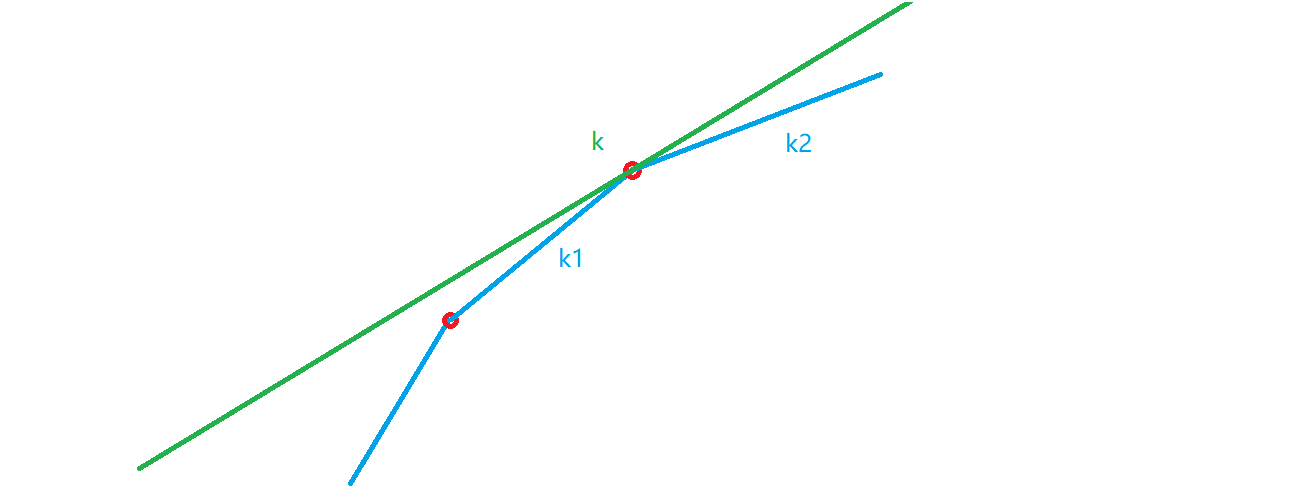
注意到 \(S2_i\) 并不一定递增，所以必须在凸壳上二分找到第一个 \(<k=S2_i\) 即小于当前直线斜率的转移点。然后进行转移。

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long LL;
#define PII pair<int,int>
const LL INF=1e18;
const int N=2e5+10;
int n;
int q[N];
LL a[N],s[N],s2[N],dp[N];

double Slope(int x,int y) {
    return ((x*s2[x]-s[x])-(y*s2[y]-s[y]))*1.0/(x*1.0-y*1.0);
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++) {
        cin>>a[i];
        s[i]=s[i-1]+1ll*i*a[i];
        s2[i]=s2[i-1]+a[i];
    }
    int l=1,r=1;
    q[1]=0;
    for(int i=1;i<=n;i++) {//维护斜率单调递减的
        int left=l,right=r;
        while(left<right) {//找到第一个k'<s2[i]
            int mid=left+right>>1;
            if(Slope(q[mid],q[mid+1])<s2[i]*1.0) right=mid;
            else left=mid+1;
        }
        LL p=q[left];//最佳转移点
        // cout<<"DEBUG:"<<i<<" "<<p<<endl;
        dp[i]=s[i]-s[p]-p*(s2[i]-s2[p]);
        while(l<r&&Slope(q[r-1],q[r])<=Slope(q[r],i)) r--;
        q[++r]=i;
    }
    LL ans=0;
    for(int i=1;i<=n;i++) ans=max(ans,dp[i]);
    cout<<ans;


    return 0;
}