树状数组

在一个数组中。若你需要频繁的计算一段区间内的和，你会怎么做？，最最简单的方法就是每次进行计算，但是这需要O(N)的时间复杂度，如这个需求非常的频繁，那么这个操作就会占用大量的CPU时间，进一步想一想，你有可能会想到使用空间换取时间的方法，把每一段区间的值一次记录下来，然后存储在内存中，将时间复杂度降低到O（1），的确，对于目前的这个需求来说，已经能够满足时间复杂度上的要求，尽管带来了线性空间复杂度的提升.

但若是我们的源数据需要频繁的更改怎么办？使用上面的方案，我们需要大量的更新我们保存到内存中的区间和，而且这中间的很多更新的影响是重叠的，我们需要重复计算。例如对于数组array[10],更新了array[4]值，需要更新区间[4,5],[4,5,6],在更新[4,5,6]需要又一次的计算[4,5]，这样的更新带来了非常多的重复计算，为了解决这一问题，树状数组应运而生了。

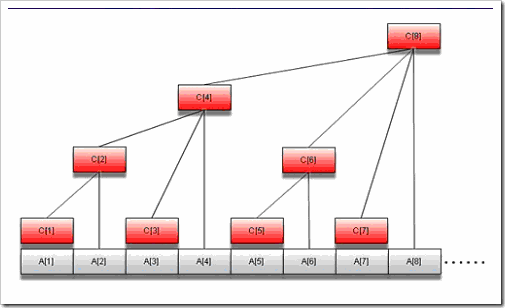
当要频繁的对数组元素进行修改,同时又要频繁的查询数组内任一区间元素之和的时候,可以考虑使用树状数组.树状数组是一种非常优雅的数据结构.先来看看一张树状结构的图片

图中C[1]的值等于A[1]，C[2]的值等于C[1]+A[2]=A[1]+a[2],C[4]的值=C[2]+C[3]=A[1]+A[2]+A[3]+A[4],假设我们现在需要更改元素a[2],那么它将只影响到得c数组中的元素有c[2],c[4],c[8],我们只需要重新计算这几个值即可，减少了很多重复的操作。这就是树状结构大致的一个存贮示意图，下面看看他的定义：

假设a[1...N]为原数组,定义c[1...N]为对应的树状数组:

c[i] = a[i - 2^k + 1] + a[i - 2^k + 2] + ... + a[i] （其中k为i的二进制表示末尾0的个数）

下面枚举出i由1...5的数据，可见正是因为上面的a[i - 2^k + 1]...a[i]的计算公式保证了我们C数组的正确意义，至于证明过程，大家可以翻阅相关资料..

基本操作：

对于C[i]=a[i - 2^k + 1]...a[i]的定义中，比较难以逐磨的k，他的值等于i这个数的二进制表示末尾0的个数.如4的二进制表示0100,此时k就等于2，而实际上我们还会发现2^k就是前一位的权值,即0100中,2^2=4，刚好是前一位数1的权值.所以所以2^k可以表示为n&(n^(n-1))或更简单的n&(-n)，例如：

为了表示简便，假设现在一个int型为4位,最高位为符号位

int i=3&(-3); 此时i=1，3的二进制为0011,-3的二进制为1101(负数存的是补码）所以0011&1101=1

int j=4&(-4); 此时j=4，理由同上..

所以计算2^k我们可以用如下代码：

1 int lowbit(int x)//计算lowbit
2 {
3 return x&(-x);
4 }

求和操作：

在上面的示意图中，若我们需要求sum[1..7]个元素的和，仅需要计算c[7]+c[6]+c[4]的和即可，究竟时间复杂度怎么算呢？一共要进行多少次求和操作呢？

求sum[1..k],我们需查找k的二进制表示中1的个数次就能得到最终结果，具体为什么，请见代码i-=lowbit(i)注释

1 int sum(int i)//求前i项和
2 {
3     int s=0;
4     while(i>0)
5     {
6         s+=c[i];
7         i-=lowbit(i); //这一步实际上等价于将i的二进制表示的最后一个1剪去，再向前数当前1的权个数（例子在下面），
8                       //而n的二进制里最多有log(n)个1，所以查询效率是log(n)
9                       //在示意图上的操作即可理解为依次找到所有的子节点
10     }
11     return s;
12 }

以求sum[1..7]为例,二进制为0111,右边第一个1出现在第0位上,也就是说要从a[7]开始向前数1个元素(只有a[7]),即c[7];

然后将这个1舍掉,得到6,二进制表示为0110,右边第一个1出现在第1位上,也就是说要从a[6]开始向前数2个元素(a[6],a[5]),即c[6];

然后舍掉用过的1,得到4,二进制表示为0100,右边第一个1出现在第2位上,也就是说要从a[4]开始向前数4个元素(a[4],a[3],a[2],a[1]),即c[4].

所以s[7]=c[7]+c[6]+c[4]

给源数组加值操作:

在上面的示意图中，假设更改的元素是a[2],那么它影响到得c数组中的元素有c[2],c[4],c[8]，我们只需一层一层往上修改就可以了,这个过程的最坏的复杂度也不过O(logN);

void add(int i,int val)
{
    while(i<=n)
    {
        c[i]+=val;
        i+=lowbit(i); //i+（i的二进制中最后一个1的权值,即2^k）,在示意图上的操作即为提升一层，到上一层的节点.
                           //这个过程实际上也只是一个把末尾1后补0的过程（例子在下面）
    }
}

以修改a[2]元素为例，需要修改c[2],2的二进制为0010,末尾补0为0100,即c[4]

4的二进制为0100，在末尾补0为1000即c[8]。所以我们需要修改的有c[2],c[4],c[8]

POJ上面有一个这方面的水题，可以帮助理解 http://poj.org/problem?id=2352

解题报告http://hi.baidu.com/acmerskycoding/blog/item/40af1b2585dd310a4c088d95.html