第六周了加油鸭

---恢复内容开始---

山师第六周学习心得

一.高数重点小结

1.导数

•即函数变化率的极限

2.函数的求导法则

 •函数的和差积商求导法则与复合函数求导法则（高中内容不再赘述）

•反函数的求导法则

[f ^-1（x₀）]'=\(\frac{1}{f'(y)}\)

3.函数在某处连续、可导、极限存在的证明比较

•可倒一定连续，连续不一定可导

（哈哈哈哈哈哈哈哈嗝）

•在某处连续：（1）：\(\lim\limits_{x\rightarrow x_0}f{\left(x\right)}=f{\left(x_0\right)}\) （2）f（x₀⁺）=f（x₀^-）

•在某处可导：（1）f '_-（x₀）=f '₊（x₀）　

•极限存在：（1）f （x₀^-）=f （x₀^-）

 4.高阶导数

重难点：莱布尼茨公式（计算时注意是否有某一项因式求导后为零）

5.隐函数求导

•一般方法：等式两边分别求导（y相当于复合函数，求导时注意准确性）

•对数求导法：适用于(1)幂指函数

　　　　　　             (2)多因子乘幂函数

二.c语言重点小结

1.课堂内容

  • 利用数组处理批量数据：

   定义一维数组a[n],方括号内的下标从0开始，可以包括常量和符号常量，不能包含变量，不可越界（无法检测出来此错误）

　•运用数组的一些算法

（1）除留余数法将十进制数转化为二进制数;

 

#include<stdio.h> 
int main()
{
    int a[100];
    int n,i=0;
    scanf("%d",&n);
    while(n!=0)//n最后为0时取余结束 
    {
        a[i]=n%2;//取余数 
        n=n/2;
        i++;
    }
    for(int j=i-1;j>=0;j--)//将余数倒序输出
        printf("%d",a[j]);
        return 0;
}

 结果：

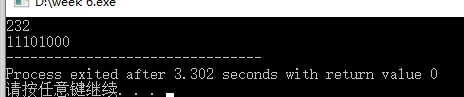
（2）.将一串数字逆置

#include<stdio.h> 
main()
{
    int j;
    scanf("%d",&j);
    int a[j];
    int i,t;
    for(i=0;i<j;i++)
        scanf("%d",&a[i]);
    for( i=0;i<j/2;i++)//将对称的元素互换（若写为i<j，则会互换两次，数字回到了原位） 
    {
    t=a[i];
    a[i]=a[j-i-1];
    a[j-i-1]=t;//第i个元素与第j-i-1个元素互换 
    }
    for(i=0;i<j;i++)
        printf("%d",a[i]);
        return 0;
}

结果：

 

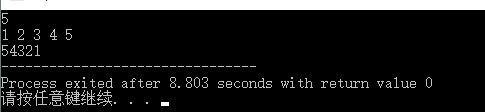
2.自学内容

 选择排序

从第一个元素开始，依次将其与后的元素相比并与最小的那个元素进行交换，n轮比较后各元素即可按由小到大的顺序排列。

冒泡排序

每次将相邻两个数进行比较，将较小的那个数调到前面，再进行下一趟两两比较，直到最小的数“上浮”到第一个。

（若有n个数，要进行n-1次比较，在第一趟比较中要进行n-1次两两比较，在第j次比较中要进行n-j次两两比较）

三．英语积累汇总

1.语法知识点

（1）虚拟语气从句为if+had done,主句为would+had done,可省略if,助动词had提前。

　　　　例句:If I had known what this week's lecture was about,I wouldn't have gone.

　　　　　　 Had I known what this week's lecture was about,I wouldn't have gone.

（2）with+符合宾语（宾语后加上作宾部的adj，adv或非谓语动词）表原因或伴随。

　　　　例句：The music was playing loudly,I coudn't concentrate.

　　　　　　　With the music played loudly,I coudn't concentrate.

2.词汇积累

 essential 必要的   clutter 杂乱的   amass 积累

  fussy 爱挑剔的，难取悦的   thereby 由此   indiscriminate 任意的

四.学习感悟（？）

高数学习成果的巩固要靠刷题。。。

C语言要天天练手。。。

---恢复内容结束---