第三周啦啊啊啊啊啊

 

 

 

山师第三周

一.高数小结

　　1.无穷小与无穷大

• 定理1 在x→x0（或x→∞）中，f（x）具有极限A的充要条件是f（x）=A+α，其中α是无穷小（可用于证明极限运算法则定理三）

　　2.极限运算法则

      • 不存在减法运算

       3.极限存在准则  两个重要极限

          •夹逼准则（重难点）

准则I 如果数列{xn},{yn}及{zn}满足下列条件：

（1）yn≤xn≤zn(n=1,2,3,……），

（2）lim n→∞ yn =a，lim n→∞ zn =a，

那么数列{xn}的极限存在，且lim n→∞ xn =a。

准则I'F(x)与G(x)在Xo连续且存在相同的极限A

limF(x)＝limG(x)＝A

则若有函数f(x)在Xo的某领域内恒有

F(x)≤f(x)≤G(x)

则当X趋近Xo有limF(x)≤limf(x)≤limG(x)

进而有 A≤limf(x)≤A  f(Xo)＝A

            •数列有界+单调一定收敛

　　    收敛必有界，无界必发散，有界不一定收敛

          •两个重要极限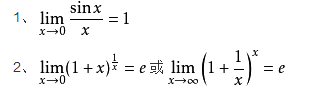

　　　　　　*求数列极限时可将式子凑出以上几种形式

二.C语言小结

课堂部分

1.类型转换

char→int→double←float

2.复合赋值运算  例：a=3,a+=a*=5，a=30.(从右向左运算)

自学部分（接上周）

牛顿迭代法（用于求方程的根）

先任意选出一个近似根x0，求出f（x0），过点（x0， f（x0））做切线交x轴于x1，求出f（x1）......直到足够接近真实根为止。

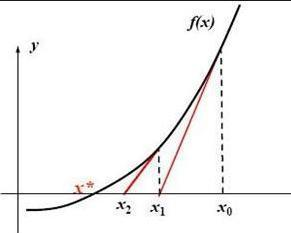
例：用牛顿迭代法求下面方程在1.5附近的根：
2x3-4x2+3x-6=0

 

 

#include <stdio.h>
 #include <math.h>
int  main()
 {double x1,x0,f,f1;
  x1=1.5;
  do
   {x0=x1;
    f=((2*x0-4)*x0+3)*x0-6;
    f1=(6*x0-8)*x0+3;
    x1=x0-f/f1;
   }while(fabs(x1-x0)>=1e-5);
  printf("The root of equation is %5.2f\n",x1);
  return 0;
 }

结果为