支持向量机
支持向量机
一、线性模型
找一个平面，向上或向下评选移动该平面，使之擦过一些向量，将距离 \(d\) 定义为此平面的优化量度，使 \(d\) 尽可能的大，\(d\) 叫做间距（margin），擦过的向量叫做支持向量（support vectors），即$ B_8$ 和 \(A_5\)。
设空间有 \(N\) 个向量 \(x_1,x_2,...x_N\)，它们要么属于 \(c_1\) 类，要么属于 \(c_2\) 类。即，
- 优化问题
最小化（Minimize）: \(\frac{1}{2}||\omega||^2\)
限制条件（Subject to）：\(y_i[\omega^Tx_i+b]\geq 1(i=1,2,...N)\)
那么优化问题为什么要最小化 \(\frac{1}{2}||\omega||^2\) 呢？首先先了解两个“事实”。
（1）若 \(\omega^T+b=0\) 表示一个平面，那么 \(a\omega^T+ab=0\) 在 \(a\in R^+\)（正实数） 的情况下表示的平面是同一个平面。
（2）点 \((x_0,y_0)\) 到平面 \(\omega_1x+\omega_2y+b=0\) 的距离 \(s=\frac{|\omega_1x_0+\omega_2y_0+b|}{\sqrt{\omega_1^2+\omega_2^2}}\)，那么根据推广可知，向量 \(x_0\) 到超平面 \(\omega^Tx+b=0\) 的距离为 \(d=\frac{\omega^Tx_0+b}{||\omega||}(||\omega||=\sqrt{\omega_x^2+\omega_2^2+...+\omega_N^2})\)。
我们可以用 \(a\) 去缩放 \((\omega,b)\rightarrow (a\omega,ab)\) ，使得 \(|\omega_*^Tx_0+b_*|=1\)，那么此时，间隔 \(d=\frac{1}{||\omega||}\) ，我们的目的是使得 \(d\) 尽可能的大，那么根据距离公式，可以使 \(||\omega||^2\) 最小化（\(\frac{1}{2}\) 是为了求导方便，没有实际意义）以达到目的。
扩展：上述优化问题是凸优化问题（也叫二次规划），特点是要么无解，要么只有一个极值。定义为
（1）目标函数是二次项。
（2）限制条件是一次项。
二、非线性模型
在线性不可分的情况下，优化问题可以写成：
最小化：\(\frac{1}{2}||\omega||+C\sum_{i=1}^{N}\delta_i\)
限制条件：（1）\(\delta_i\geq0\)；（2）\(y_i[\omega^Tx_i+b]\geq 1-\delta_i(i=1,2,...,N)\)
注意：
（1）\(C\)是常数，是事先设定好的，为了平衡权重。\(\omega,b,\delta_i(i=1,2,...,N)\) 为待求变量。
（2）此优化问题（也是凸优化）对任意点集，无论是否线性可分都有解。
支持向量机处理非线性情况是通过将向量 \(x\) 映射到高维空间，再用线性方式去分开。通俗的说，在低纬空间线性不可分，那么在高维有很大的概率能够线性可分。例如异或问题是线性不可分的。
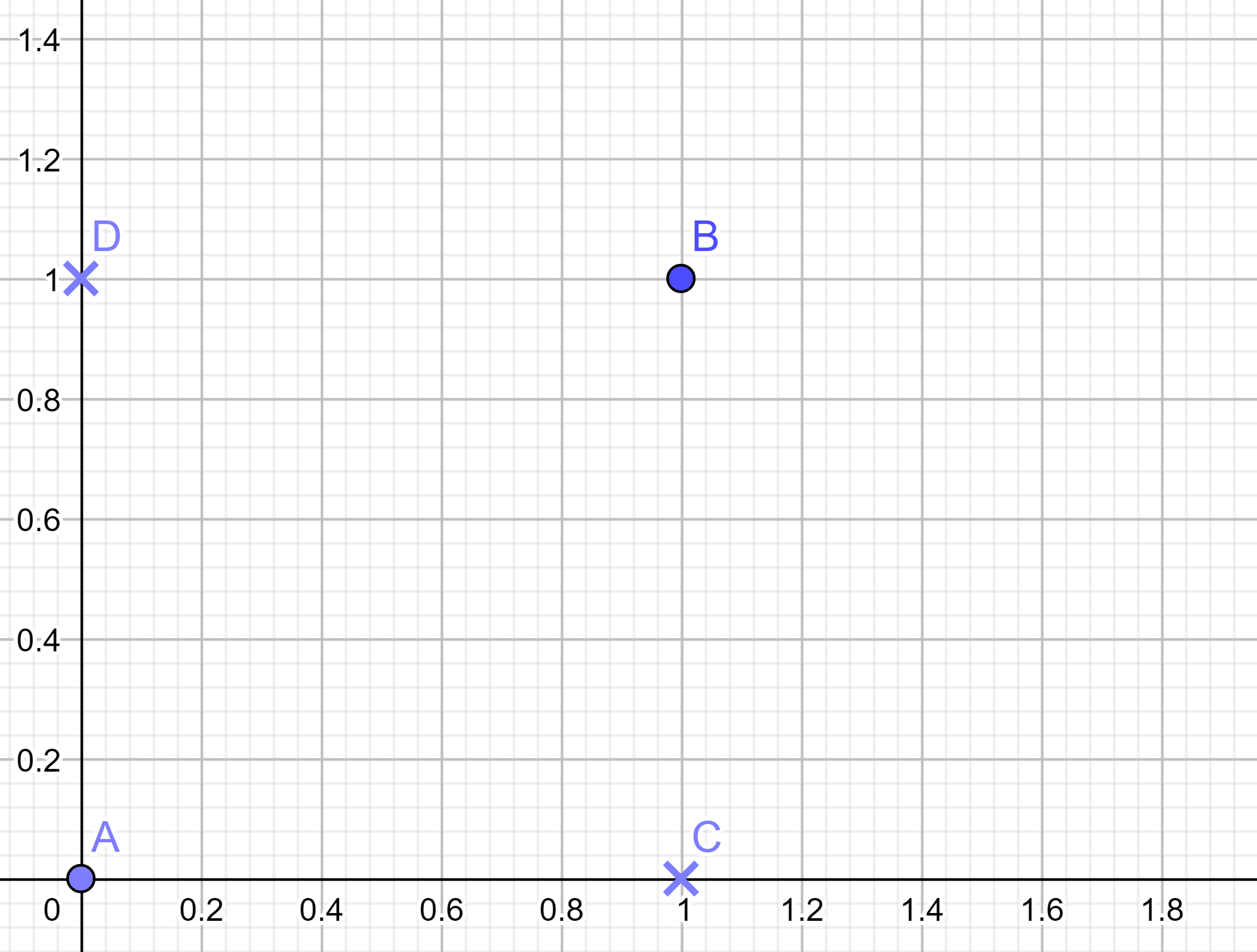
设 \(A=\left[\begin{matrix} 0\\ 0 \end{matrix} \right] \in c_1 ,\quad B=\left[\begin{matrix} 1\\ 1 \end{matrix} \right] \in c_1 ,\quad C=\left[\begin{matrix} 1\\ 0 \end{matrix} \right] \in c_2 ,\quad D=\left[\begin{matrix} 0\\ 1 \end{matrix} \right] \in c_2\) ，让 \(x\) 通过 \(\varphi(x)\) 变换映射到高维空间。即
那么
那么可以找到一组解使其线性可分，即
代入式子可得如下式子，显然线性可分。
当 \(\varphi(x)\) 接近无限维度时，线性可分的概率会接近到1，对于此问题，只需要修改 SVM 中 \(x\) 为\(\varphi(x)\) 即可。
最小化：\(\frac{1}{2}||\omega||+C\sum_{i=1}^{N}\delta_i\)
限制条件：（1）\(\delta_i\geq0\)；（2）\(y_i[\omega^T\varphi(x_i)+b]\geq 1-\delta_i(i=1,2,...,N)\)
\(\varphi(x)\) 这会是一个非常复杂的式子。其实我们不需要知道 \(\varphi(x)\) 的显示表达也可以计算。我们只需要知道一个核函数（kernel function），即 \(k(x_1,x_2)=\varphi(x_1)^T\varphi(x_2)\) 就可以了。
- 常用的核函数有如下：
| 名称 | 表达式 |
|---|---|
| 线性核 | \(k(x_i,x_j)=x_i^Tx_j\) |
| 多项式核 | \(k(x_i,x_j)=(x_i^Tx_j)^d\) |
| 高斯核 | $k(x_i,x_j)=exp(-\frac{ |
| sigmoid核 | \(k(x_i,x_j)=tanh(\beta x^T_ix_j +\theta)\) |
\(Mercer's \quad Theorem\) :核函数 \(k(x_1,x_2)\) 可拆分为 \(\varphi(x_1)^T \varphi(x_2)\) 的充分条件为：对任意函数 \(\varphi(x)\) 满足 :
\[(1)\quad k(x_1,x_2)=k(x_2,x_1)(交换律) \quad;\quad(2)\quad \forall c_i,x_i(x=1...N),\sum_{i=1}^{N}\sum_{j=1}^{N}c_ic_jk(x_i,x_j) \geq 0(半正定性) \]
- 原问题（Prime Problem）与对偶问题(Dual Problem)
（1）原问题：
最小化（Minimize）: \(f(\omega)\)
限制条件（Subject to）: \(g_i(\omega) \le 0(i=1,2...K) \quad ;\quad h_i(\omega)=0(i=1,2,...M)\)
（2）对偶问题：
定义：\(L(\omega,\alpha,\beta) = f(w)+\sum_{i=1}^{K}\alpha_ig_i(\omega)+\sum_{i=1}^{M}\beta_i h_i(\omega)=f(\omega)+\alpha^Tg(\omega)+\beta^Th(\omega)\)
最大化（Maximize）: \(\theta(\alpha,\beta) = inf_{定义域内所有的\omega}L(\omega,\alpha,\beta)\)
\((inf即求最小值，该式是在\alpha,\beta 固定下，遍历\omega，求最小值)\)
限制条件（Subject to）: $\alpha_i \ge 0(i=1,2,...K) $
（3）定理1：如果 \(\omega^*\) 是原问题的解，而 \(\alpha^*,\beta^*\) 是其对偶问题的解，则有 \(f(\omega^*) \ge \theta(\alpha^*,\beta^*)\)
证明：
\[\begin{aligned} \theta(\alpha^*,\beta^*) & = inf_{定义域内所有的\omega}L(\omega^*,\alpha^*,\beta^*)\\ &\le L(\omega^*,\alpha^*,\beta^*) \\ &=f(\omega^*)+\underbrace{\alpha^{*T}}_{\ge0} \underbrace{g(\omega^*)}_{\le0}+\beta^{*T}\underbrace{h(\omega^*)}_{=0} \\ &\le f(\omega^*) \end{aligned} \]\(G = f(\omega^*) - \theta(\alpha^*,\beta^*) \ge0\) 叫原问题与对偶问题的间距（Duality Gap）。
注意：如果 \(f(\omega^*) = \theta(\alpha^*,\beta^*)\)，必能推出对于所有的 \(i=1-K,\alpha_i^* = 0 或 g_i^*(\omega^*)=0\) ,此为 \(KKT\) 条件。
（4）定理2（强对偶定理）：如果 \(g(\omega) = A\omega +b，h(\omega) = C\omega+d,f(\omega)\) 为凸函数，则 \(f(\omega^*) = \theta(\alpha^*,\beta^*)\)，即间距为0。
凸函数定义是\(\forall \omega_1,\omega_2\)，有 \(f(\lambda\omega_1+(1-\lambda)\omega_2)\le\lambda f(\omega_1)+(1-\lambda)f(\omega_2) \quad \lambda\in[0,1]\)
- 支持向量机（原问题与对偶问题）
（1）原问题
最小化：\(\frac{1}{2}||\omega||-C\sum_{i=1}^{N}\delta_i\)
限制条件：（1）\(\delta_i\le0\)；（2）\(1+\delta_i-y_i\omega^T\varphi(x_i)+y_ib\le 0(i=1,2,...,N)\)
（2）对偶问题
最大化 \(\theta(\alpha,\beta) = inf_{所有 \omega,\delta_i,b}\frac{1}{2}||\omega||^2-C\sum_{i=1}^{N}\delta_i+\sum_{i=1}^N\beta_i\delta_i+\sum_{i=1}^N\alpha_i[1+\delta_i-y_i\omega^T\varphi(x_i)+y_ib]\)
限制条件：（1）\(\alpha_i\ge0(i=1,2,...,N)\)；（2）\(\beta_i\ge0(i=1,2,...,N)\)
现在的待求参数是 \(\omega ,\delta_i ,b\)，对其求偏导，并等于0处取得最优值。
\[\begin{aligned} &\frac{\partial \theta}{\partial \omega} = \omega-\sum_{i=1}^{N}\alpha_i\varphi(x_i)y_i=0\Longrightarrow \omega=\sum_{i=1}^{N}\alpha_i\varphi(x_i)y_i \qquad (1) \\ &\frac{\partial \theta}{\partial \delta_i}=-C+\beta_i+\alpha_i=0\Longrightarrow \alpha_i+\beta_i=C \qquad (2) \\ &\frac{\partial \theta}{\partial b} = -\sum_{i=1}^N\alpha_iy_i=0\Longrightarrow\sum_{i=1}^N\alpha_iy_i =0\qquad(3) \end{aligned} \]
把（1）（2）（3）代入后的对偶问题为
最大化：
\(\theta(\alpha,\beta)=\sum_{i=1}^N-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^{N}y_iy_j\alpha_i\alpha_j\varphi(x_i)^T\varphi(x_j)=\sum_{i=1}^N-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^{N}y_iy_j\alpha_i\alpha_jk(x_i,x_j)\)
限制条件：
（1）\(0\le\alpha_i\le C(因为\beta_i\ge0且\beta_i=C-\alpha_i,所以 \alpha_i \le C,i=1,2,...,N)\)；
（2）\(\sum_{i=1}^{N}\alpha_iy_i=0(i=1,2,...,N)\)
这也是一个二次规划问题，解此问题时，由于 \(\varphi(x_i)^T\varphi(x_j)=k(x_i,x_j)\)，我们只需要知道核函数，不需要知道 \(\varphi(x)\) 的具体表达。现在我们计算 \(\omega^T\varphi(x_i) +b\)。
首先计算 \(\omega^T \varphi(x_i)\)，根据（1）式子可得 \(\omega^T \varphi(x_i) = \sum_{j=1}^{N}y_j\alpha_j\varphi(x_j)^T\varphi(x_i)=\sum_{j=1}^{N}y_j\alpha_jk(x_j,x_i)\)
然后算 \(b\)，根据KKT条件，对于所有 \(i(i=1,2...N)\) 有 \(\alpha_i[1+\delta_i-y_i\omega^T\varphi(x_i)+y_ib] = 0\) 且 \(\beta_i\delta_i = 0 \Longrightarrow(C-\alpha_i)\delta_i = 0\)，如果对于某一个 \(i，\alpha_i \not=0，且\alpha_i \not=C\)，则必有 \(\delta_i=0(由\beta_i\not=0推出)\)，\(1+\delta_i-y_i\omega^T\varphi(x_i)+y_ib=0(由\alpha_i\not=0推出)\)，因此 \(b\) 的值为
\[b=\frac{1-y_i\omega^T\varphi(x_i)}{y_i} =\frac{1-y_i\sum_{j=1}^N\varphi_jy_jk(x_i,x_j)}{y_i} \]
最后，我们可以对测试样本 \(x\) 进行判断，即
