卷积特征提取

卷积特征提取

 

概述

前面的练习中，解决了一些有关低分辨率图像的问题，比如：小块图像，手写数字小幅图像等。在这部分中，我们将把已知的方法扩展到实际应用中更加常见的大图像数据集。

 

全联通网络

在稀疏自编码章节中，我们介绍了把输入层和隐含层进行“全连接”的设计。从计算的角度来讲，在其他章节中曾经用过的相对较小的图像（如在稀疏自编码的作业中用到过的 8x8 的小块图像，在MNIST数据集中用到过的28x28 的小块图像），从整幅图像中计算特征是可行的。但是，如果是更大的图像（如 96x96 的图像），要通过这种全联通网络的这种方法来学习整幅图像上的特征，从计算角度而言，将变得非常耗时。你需要设计 10 的 4 次方（=10000）个输入单元，假设你要学习 100 个特征，那么就有 10 的 6 次方个参数需要去学习。与 28x28 的小块图像相比较， 96x96 的图像使用前向输送或者后向传导的计算方式，计算过程也会慢 10 的 2 次方（=100）倍。

 

部分联通网络

解决这类问题的一种简单方法是对隐含单元和输入单元间的连接加以限制：每个隐含单元仅仅只能连接输入单元的一部分。例如，每个隐含单元仅仅连接输入图像的一小片相邻区域。（对于不同于图像输入的输入形式，也会有一些特别的连接到单隐含层的输入信号“连接区域”选择方式。如音频作为一种信号输入方式，一个隐含单元所需要连接的输入单元的子集，可能仅仅是一段音频输入所对应的某个时间段上的信号。）

网络部分连通的思想，也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的（即这些神经元只响应某些特定区域的刺激）。

 

卷积

自然图像有其固有特性，也就是说，图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上，所以对于这个图像上的所有位置，我们都能使用同样的学习特征。

更恰当的解释是，当从一个大尺寸图像中随机选取一小块，比如说 8x8 作为样本，并且从这个小块样本中学习到了一些特征，这时我们可以把从这个 8x8 样本中学习到的特征作为探测器，应用到这个图像的任意地方中去。特别是，我们可以用从 8x8 样本中所学习到的特征跟原本的大尺寸图像作卷积，从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。

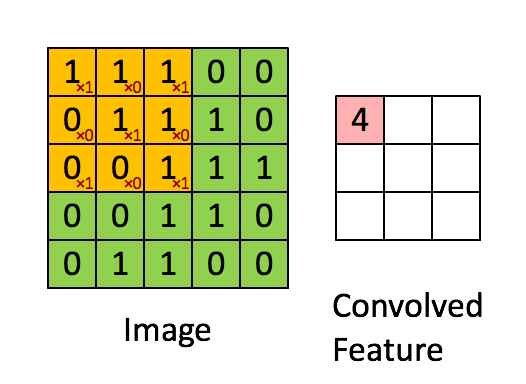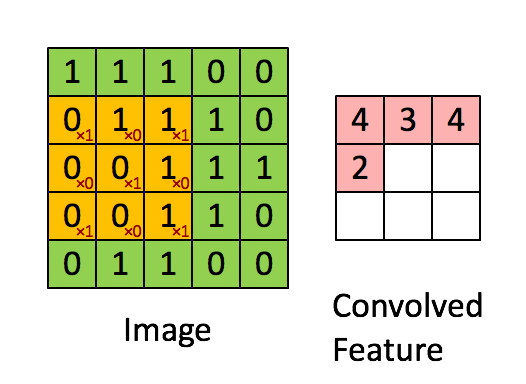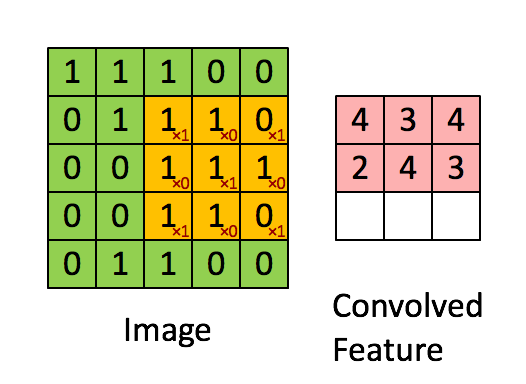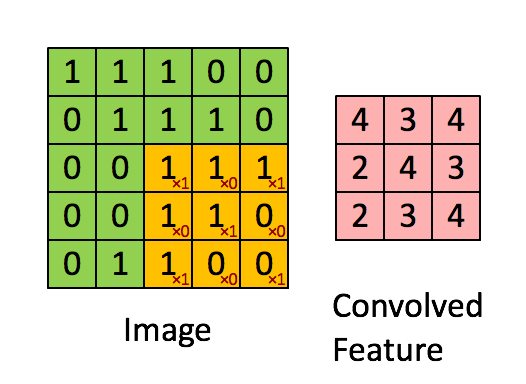
下面给出一个具体的例子：假设你已经从一个 96x96 的图像中学习到了它的一个 8x8 的样本所具有的特征，假设这是由有 100 个隐含单元的自编码完成的。为了得到卷积特征，需要对 96x96 的图像的每个 8x8 的小块图像区域都进行卷积运算。也就是说，抽取 8x8 的小块区域，并且从起始坐标开始依次标记为（1，1），（1，2），...，一直到（89，89），然后对抽取的区域逐个运行训练过的稀疏自编码来得到特征的激活值。在这个例子里，显然可以得到 100 个集合，每个集合含有 89x89 个卷积特征。

假设给定了 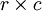 的大尺寸图像，将其定义为 x_large。首先通过从大尺寸图像中抽取的  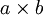的小尺寸图像样本 x_small 训练稀疏自编码，计算 f = σ(W⁽¹⁾x_small + b⁽¹⁾)（σ是一个 sigmoid 型函数）得到了 k 个特征， 其中 W⁽¹⁾ 和 b⁽¹⁾ 是可视层单元和隐含单元之间的权重和偏差值。对于每一个  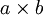大小的小图像 x_s，计算出对应的值 f_s = σ(W⁽¹⁾x_s + b⁽¹⁾)，对这些 f_convolved 值做卷积，就可以得到  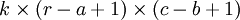个卷积后的特征的矩阵。

在接下来的章节里，我们会更进一步描述如何把这些特征汇总到一起以得到一些更利于分类的特征。

 

中英文对照

全联通网络 Full Connected Networks

稀疏编码 Sparse Autoencoder

前向输送 Feedforward

反向传播 Backpropagation

部分联通网络 Locally Connected Networks

连接区域 Contiguous Groups

视觉皮层 Visual Cortex

卷积 Convolution

固有特征 Stationary

池化 Pool