数据结构与算法系列(二)-- 算法
本节目录
排序
- 一、冒泡排序
- 二、选择排序
- 三、插入排序
- 四、快速排序
- 五、堆排序
- 六、归并排序
- 七、NB三人组总结
- 八、希尔排序
- 九、计数排序
- 十、桶排序
- 十一、基数排序
查找
- 一、顺序查找
- 二、二分查找
递归
- 汉诺塔问题
贪心算法
- 定义
- 找零问题
- 背包问题
- 拼接最大数字问题
- 活动选择问题
- 贪婪算法的弊端
- 什么问题适用贪婪算法
动态规划
- 斐波那契数列
- 钢条切割问题
- 最长公共子序列
欧几里得算法
RSA加密算法
什么是算法?
"""
时间复杂度:衡量算法执行效率的快慢
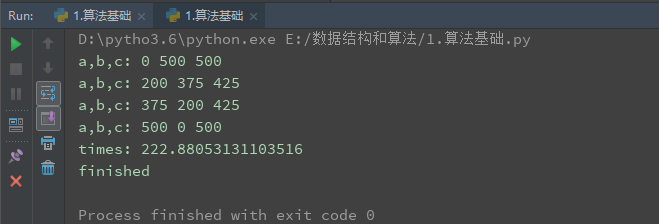
a+b+c=1000,且a^2+b^2=c^2(a,b,c为自然数),如何求出所有a,b,c的自然数组合?
a,b,c
总时间=基本运算数量*执行次数
每台机器执行的总时间不同
但是执行基本运算数量大体相同
"""
import time
start_time = time.time()
# for a in range(1001):
# for b in range(1001):
# for c in range(1001):
# if a+b+c==1000 and a**2+b**2==c**2:
# print('a,b,c:',a,b,c) #222秒
"""
T = 1000 * 1000 * 1000 * 2
T = 2000 * 2000 * 2000 * 2
T = N * N * N *2
T(n) = n^3 * 2
T(n) = n^3 * 10
T(n) = n^3 * k
从数学上,T(n) = k*g(n),在现实中,省去细枝末叶,只剩下最显著特征
T(n) = g(n)
g(n) = n^3
"""
#顺序
#条件
#循环
for a in range(1001):
for b in range(1001):
c = 1000-a-b
if a**2+b**2==c**2:
print('a,b,c:',a,b,c) #1秒
end_time = time.time()
print('times:',end_time-start_time)
print('finished')
"""
T(n) = n * n *(1+max(1,0))
= n^2*2
= 〇(n^2)
"""

示例2:列表效率对比

from timeit import Timer """ li1 = [1,2] li2 = [23,5] li = li1 + li2 li = [i for i in range(10000)] li = list(range(10000)) """ def t1(): li = [] for i in range(10000): li.append(i) def t2(): li = [] for i in range(10000): # li = li + [i] #218秒 li += [i] #1.04 def t3(): li = [i for i in range(10000)] def t4(): li = list(range(10000)) def t5(): li = [] for i in range(10000): li.extend([i]) timer1 = Timer("t1()","from __main__ import t1") print('append:',timer1.timeit(1000)) timer2 = Timer("t2()","from __main__ import t2") print('+:',timer2.timeit(1000)) timer3 = Timer("t3()","from __main__ import t3") print('[i for i in range]:',timer3.timeit(1000)) timer4 = Timer("t4()","from __main__ import t4") print('list(range())',timer4.timeit(1000)) timer5 = Timer("t5()","from __main__ import t5") print('extend:',timer5.timeit(1000)) def t6(): li = [] for i in range(10000): li.append(i) def t7(): li = [] for i in range(10000): li.insert(0,i) # timer6 = Timer("t6()","from __main__ import t6") # print('append:',timer6.timeit(1000)) timer7 = Timer("t7()","from __main__ import t7") print('insert:',timer7.timeit(1000)) #16,33s/test/t #查找和替换 """ 数据结构是指数据对象中数据元素之间的关系 程序设计语言基本数据类型:int,float,string,char Python内置数据结构:list,dict,tuple. Python扩展数据结构:栈,队列 """ """ name age hometown [ ('zhangsan',24,'beijing'), ('zhangsan',24,'beijing'), ('zhangsan',24,'beijing'), ] class Stus(object): def adds(self):pass def pop(self):pass def sort(self):pass def modify(self):pass for stu in stus: if stu[0] == 'zhangsan': [ {'name':'zhangsan'}, {'age':23}, {'hometown':'beijjing'}, ] { 'zhangsan':{ 'age':24, 'hometown':'beijing', } } stu['zhangsan'] """

import sys from timeit import Timer reps = 1000 size = 10000 def forStatement(): res = [] for x in range(size): res.append(abs(x)) # 列表解析 def listComprehension(): res = [abs(x) for x in range(size)] # map def mapFunction(): res = list(map(abs, range(size))) # 生成器表达式 def generatorExpression(): res = list(abs(x) for x in range(size)) if __name__ == '__main__': print(sys.version) timer1 = Timer("forStatement()", "from __main__ import forStatement") print('for循环append', timer1.timeit(reps)) timer2 = Timer("listComprehension()", "from __main__ import listComprehension") print('列表推导式', timer2.timeit(reps)) timer3 = Timer("mapFunction()", "from __main__ import mapFunction") print('map:', timer3.timeit(reps)) timer4 = Timer("generatorExpression()", "from __main__ import generatorExpression") print('生成器表达式', timer4.timeit(reps)) # 3.6.5 (v3.6.5:f59c0932b4, Mar 28 2018, 17:00:18) [MSC v.1900 64 bit (AMD64)] # for循环append 1.786315169601012 # 列表推导式 1.031664329539618 # map: 0.5723600621124123 # 生成器表达式 1.4653949103231731



时间复杂度
-
用来评估算法运行效率的一个式子(单位)
-
运行时间跟电脑性能等因素有关,不好精确的衡量。
-
有些对比运行时间过长不好操作,需要通用的公式进行直观的衡量。
-
一般来说,时间复杂度高的算法比复杂度低的算法慢
-
常见的时间复杂度(按效率排序)
O(1)< O(logn) < O(nlogn) < O(n2) < O(n2logn) < O(n3)
-


-
复杂问题的时间复杂度
O(n!)O(2n) O(nn)
-
快速判断算法复杂度
-
确定问题规模N
-
循环减半过程 - > logn
-
k层关于n的循环 -> nk
-
-
复杂情况:根据算法执行过程判断
空间复杂度
-
用来评估算法内存占用大小的式子
-
空间复杂度的表示方式与实践复杂度完全一样
-
算法使用了几个变量:O(1)
-
算法使用了长度为n的一维列表:O(n)
-
算法使用了m行n列的二维列表:O(mn)
-
-
空间换时间
排序
-
-
列表排序:将无序列表变为有序列表
-
输入:列表
-
输出:有序列表
-
-
升序与降序
-
内置排序函数:sort()
-
常见的排序算法
排序LowB三人组 排序NB三人组 其他排序 冒泡排序 快速排序 希尔排序 选择排序 堆排序 计数排序 插入排序 归并排序 基数排序
一、 冒泡排序(Bubble Sort)
-
算法思想
每⼀轮,从杂乱⽆章的数组头部开始,每两个元素⽐较⼤⼩并进⾏交换;
直到这⼀轮当中最⼤或最⼩的元素被放置在数组的尾部; 然后,不断地重复这个过程,直到所有元素都排好位置
列表每两个相邻的数,如果前面比后面的大,则交换这两个数据
一趟排序完成后,则无序区减少一个数,有序区增加一个数 -
代码关键点:趟、无序区范围
-
代码实现
def bubble_sort2(alist): """冒泡排序,每一次循环找出最大值""" n = len(alist) for i in range(n - 1, 0, -1): for j in range(i): if alist[j] > alist[j + 1]: alist[j], alist[j + 1] = alist[j + 1], alist[j] def bubble_sort(alist): """冒泡排序,每一次循环找出最大值 改进版""" n = len(alist) for i in range(n - 1): # n - 1 趟 exchange = False for j in range(n - i - 1): # 无序区中最大的数移到有序区 if alist[j] > alist[j + 1]: alist[j], alist[j + 1] = alist[j + 1], alist[j] exchange = True if exchange: return -
空间复杂度:O(1)
假设数组的元素个数是n,整个排序的过程中,直接在给定的数组⾥进⾏元素的两两交换
-
时间复杂度:O(n2)
情景⼀:给定的数组按照顺序已经排好 只需要进⾏n - 1次的⽐较,两两交换次数为0,时间复杂度是O(n),这是最好的情况。
情景⼆:给定的数组按照逆序排列 需要进⾏n(n - 1) / 2次⽐较,时间复杂度是O(n^2),这是最坏的情况。
情景三:给定的数组杂乱⽆章 在这种情况下,平均时间复杂度是O(n^2
二、 选择排序
- 算法流程
-
一趟排序记录最小的数,放到第一个位置
-
再一趟排序记录记录列表无序区最小的数,放到第二个位置
-
-
-
算法关键点:有序区和无序区、无序区最小数的位置
-
代码
def select_sort(alist): li_new = [] for i in range(len(alist)): min_val = min(alist) li_new.append(min_val) alist.remove(min_val) return li_new def select_sort1(alist): """ 选择排序:每次选择最小或者最大 """ for i in range(len(alist)): min_v = min(alist[i:len(alist)]) j = alist.index(min_v) alist[i], alist[j] = alist[j], alist[i] def select_sort2(alist): """ 选择排序:每次选择最小或者最大 """ n = len(alist) for j in range(n - 1): # 第几趟 min_index = j for i in range(j + 1, n): if alist[min_index] > alist[i]: min_index = i alist[j], alist[min_index] = alist[min_index], alist[j] -
时间复杂度:O(n2)
三、 插入排序(Insertion Sort)
-
与冒泡排序对⽐
在冒泡排序中,经过每⼀轮的排序处理后,数组后端的数是排好序的; 在插⼊排序中,经过每⼀轮的排序处理后,数组前端的数都是排好序的。
-
算法思想
初始时手里(有序区)只有一张牌
每次(从无序区)摸一张牌,插入到手里已经有牌的正确位置
不断地将尚未排好序的数插⼊到已经排好序的部分。
-
代码实现
import random from timeit import Timer # alist = [54, 226, 93, 17, 77, 31, 44, 55, 20] # alist1 = [54, 226, 93, 17, 77, 31, 44, 55, 20] def insert_sort(alist): """插入排序""" #从第二个位置,即下标为1的元素开始向前插入 for i in range(1,len(alist)): # i表示摸到的牌的下标 for j in range(i,0,-1): #从第i个元素开始向前比较,如果小于前一个,则交换,否则终止循环 if alist[j]<alist[j-1]: alist[j-1],alist[j] = alist[j],alist[j-1] else: break def insert_sort1(alist1): """插入排序""" #从右边的无序序列中 for j in range(1,len(alist1)): #i代表内层循环起始值 i = j #执行从右边的无序序列中取出第一个元素,即i位置的元素,然后将其插入到前面的正确的位置中 while i > 0: if alist1[i]<alist1[i-1]: alist1[i],alist1[i-1] = alist1[i-1],alist1[i] i -= 1 else: break def insert_sort2(alist): for i in range(1, len(alist)): # i 表示摸到的牌的下标 tmp = alist[i] j = i - 1 # j指的是手里的牌的下标 while j >= 0 and alist[j] > tmp: alist[j + 1] = alist[j] j -= 1 alist[j + 1] = tmp -
空间复杂度:O(1)
假设数组的元素个数是n,整个排序的过程中,直接在给定的数组⾥进⾏元素的两两交换。 -
时间复杂度:O(n2)
情景⼀:给定的数组按照顺序已经排好
只需要进⾏n - 1次的⽐较,两两交换次数为0,时间复杂度是O(n),这是最好的情况。
情景⼆:给定的数组按照逆序排列
需要进⾏n(n - 1) / 2次⽐较,时间复杂度是O(n^2),这是最坏的情况。
情景三:给定的数组杂乱⽆章
在这种情况下,平均时间复杂度是O(n^2)。
四、 快速排序(Quick Sort)
-
算法思想

快速排序也采⽤了分治的思想;
把原始的数组筛选成较⼩和较⼤的两个⼦数组,然后递归地排序两个⼦数组;
在分成较⼩和较⼤的两个⼦数组过程中,如何选定⼀个基准值尤为关键。
-
代码实现
def partition(li, left, right): tmp = li[left] while left < right: while left < right and li[right] >= tmp: right -= 1 li[left] = li[right] while left < right and li[left] <= tmp: left += 1 li[right] = li[left] li[left] = tmp return left def quick_sort(li, left, right): if left < right: mid = partition(li, left, right) quick_sort(li, left, mid - 1) quick_sort(li, mid + 1, right) -
时间复杂度:O(nlogn)
最优:T(n) = 2*T(n/2) + O(n)
把规模⼤⼩为n的问题分解成n/2的两个⼦问题;
和基准值进⾏n-1次⽐较,n-1次⽐较的复杂度就是O(n);
快速排序的复杂度也是O(nlogn)。 -
空间复杂度:O(logn)
和归并排序不同,快速排序在每次递归的过程中;
⽽递归次数为logn,所以它的整体空间复杂度完全取决于压堆栈的次数。
只需要开辟O(1)的存储空间来完成交换操作实现直接对数组的修改;
五、 堆排序(Heap Sort)
-
一些概念
-
根节点、叶子节点
-
树的函数呢度(高度)
-
树的度
-
孩子节点/父节点
-
子树
-
二叉树:度不超过2的树
-
每个节点最多有两个孩子节点
-
两个孩子节点被区分为左孩子节点和右孩子节点
-
满二叉树:一个二叉树,如果每一个层的节点数都达到最大值,则这个二叉树就是满二叉树
-
完全二叉树:叶节点只能出现在最下层和此下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树。
-
-
二叉树的存储方式(表示方式)
-
链式存储方式
-
顺序存储方式

-
-
堆:一种特殊的完全二叉树结构
-
大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大。
-
小根堆:一棵完全二叉树,满足任一节点都比起孩子节点小。
-
-
堆的向下调整性质
假设:节点的左右子树都是堆,但自身不是堆
当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆。
-
堆排序过程
-
建立堆
-
得到堆顶元素为最大元素
-
去掉堆顶,将堆的最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。
-
堆顶元素为第二大元素。
-
重复步骤3,直到堆变空。
-
-
构造堆:从最后一个非叶子节点所在堆,开始依次调整堆
-
代码
def sift(li, low, high): """ 调整堆 :param li: :param low: :param high: :return: """ i = low # 开始i指向根节点 j = 2 * i + 1 # j指向i的左孩子 tmp = li[i] # 把堆顶存起来 while j <= high: # 保证j指向的节点有孩子,非叶子节点 if j + 1 <= high and li[j + 1] > li[j]: # 如何右孩子比左孩子大 j = j + 1 # j指向右孩子 if li[j] > tmp: # 如何j指向的节点大于tmp,则将j指向的节点向上调整,i和j向下移,i到j的位置 li[i] = li[j] i = j j = 2 * i + 1 else: # tmp更大 把tmp放到i的位置上 li[i] = tmp # 把tmp放到某一级领导位置上 break else: li[i] = tmp # 把tmp放到叶子节点上 def heap_sort(li): n = len(li) for i in range((n - 2) // 2, -1, -1): # i表示舰队的时候调整的部分的额根的下标 sift(li, i, n-1) # 建堆完成了 for i in range(n-1, -1, -1): li[0], li[i] = li[i], li[0] sift(li, 0, i-1) -
时间复杂度:O(nlogn)
-
堆排序的内置模块--heapq
-
常用函数
-
heapify(x)
-
heappush(heap, item)
-
heappop(heap)
-
-
-
堆排序应用--topK问题(热搜榜等)
现在有n个数,设计算法得到前k个大的数。(k<n)
解决思路:
-
排序后切片 O(nlogn)
-
排序LowB三人组 O(kn)
-
堆排序(nlogk)
-
取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数。
-
依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行一次调整;
-
遍历列表所有元素后,倒序弹出堆顶。
def topk(li, k): heap = li[0:k] for i in range((k - 2) // 2, -1, -1): sift(heap, i, k - 1) # 1. 建堆 for i in range(k, len(li) - 1): if li[i] > heap[0]: heap[0] = li[i] sift(heap, 0, k-1) # 2. 遍历 倒序弹出堆顶 for i in range(k-1, -1, -1): heap[0], heap[i] = heap[i], heap[0] sift(heap, 0, i - 1) # 每次循环找出最小的一个元素,将剩下的重新构建最小堆 # 3. 出数 return heap -
-
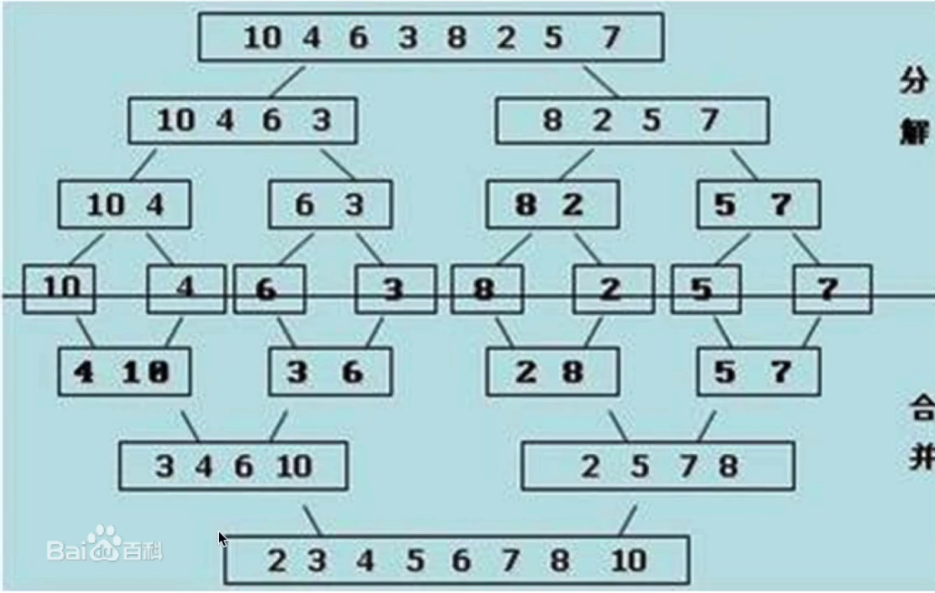
六、 归并排序(Merge Sort)

-
分治的思想
归并排序的核⼼思想是分治,把⼀个复杂问题拆分成若⼲个⼦问题来求解
-
算法思想
-
分解:将列表越分越小,直至分成一个元素。
-
终止条件:一个元素是有序的。
-
合并:将两个有序列表归并,列表越来越大。
把数组从中间划分成两个⼦数组;
⼀直递归地把⼦数组划分成更⼩的⼦数组,直到⼦数组⾥⾯只有⼀个元素;
依次按照递归的返回顺序,不断地合并排好序的⼦数组,直到最后把整个数组的顺序排好。
-
-
代码实现
-
一次归并
def merge(li, left, mid, right): i = left j = mid + 1 tmp = [] while i <= mid and j <= right: # 只要左右两边都有参数 if li[i] < li[j]: tmp.append(li[i]) i += 1 else: tmp.append(li[j]) j += 1 # while执行完 肯定有一部分没数了 while i <= mid: tmp.append(li[i]) i += 1 while j <= right: tmp.append(li[j]) j += 1 li[left: right + 1] = tmp -
归并排序
def merge(li, left, mid, right): i = left j = mid + 1 tmp = [] while i <= mid and j <= right: # 只要左右两边都有参数 if li[i] < li[j]: tmp.append(li[i]) i += 1 else: tmp.append(li[j]) j += 1 # while执行完 肯定有一部分没数了 while i <= mid: tmp.append(li[i]) i += 1 while j <= right: tmp.append(li[j]) j += 1 li[left: right + 1] = tmp def _merge_sort(li, low, high): if low < high: mid = (low + high) // 2 _merge_sort(li, low, mid) _merge_sort(li, mid + 1, high) merge(li, low, mid, high) def merge_sort(li): _merge_sort(li, 0, len(li) - 1)
-
-
时间复杂度:O(nlogn)
归并算法是⼀个不断递归的过程,假设数组的元素个数是n。
时间复杂度:T(n) 时间复杂度是T(n)的函数:T(n) = 2*T(n/2) + O(n)
对于规模为n的问题,⼀共要进⾏log(n)层的⼤⼩切分; 每⼀层的合并复杂度都是O(n); 所以整体的复杂度就是O(nlogn)。
-
空间复杂度:O(n)
由于合并n个元素需要分配⼀个⼤⼩为n的额外数组,合并完成之后,这个数组的空间就会被释放
七、 NB三人组小结
-
三种排序算法的时间复杂度都是O(nlogn)
-
一般情况下,就运行时间而言:
快速排序 > 归并排序 > 堆排序
-
三种排序算法的缺点:
快速排序:极端情况下排序效率低
归并排序:需要额外的内存开销
堆排序:在快的排序算法中相对较慢
排序方法 时间复杂度 空间复杂度 稳定性 最坏情况 平均情况 最好情况 冒泡排序 O(n2) O(n2) O(n) O(1) 稳定 直接选择排序 O(n2) O(n2) O(n2) O(1) 不稳定 直接插入排序 O(n2) O(n2) O(n2) O(1) 稳定 快速排序 O(n2) O(nlogn) O(nlogn) 平均情况O(nlogn) 最坏情况O(n) 不稳定 堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) 不稳定 归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 稳定
八、希尔排序
-
希尔排序是一种分组插入排序算法
-
算法思想
-
首先取一个整数d1=n/2,将元素分为d1个组,每组相邻元素之间距离为d1,在各组内进行直接插入排序;
-
取第二个整数d2=d1/2,重复上述分组排序过程,直到di=1,即所有元素子啊同一组内进行直接插入排序。
-
希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。
-
-
代码
def shell_sort(li): """ 希尔排序 :param li: :return: """ gap = len(li) // 2 while gap >= 1: for i in range(gap, len(li)): tmp = li[i] j = i - gap while j >= 0 and li[j] > tmp: li[j+gap] = li[j] j -= gap li[j + gap] = tmp gap //= 2 -
希尔排序的时间复杂度比较复杂,与gap有关,在这不做讨论。
九、计数排序
-
对列表进行排序,列表中的数范围都在0到100之间。设计时间复杂度为O(n)的算法。
-
代码
def count_sort(li: list, max_count: int = 100): count_list = [0 for _ in range(max_count + 1)] for val in li: count_list[val] += 1 li.clear() for index, val in enumerate(count_list): li += [index for _ in range(val)]
十、桶排序
-
在计数排序中,如果元素的范围比较大(比如在1到1亿之间),如何改造算法?
-
桶排序(Bucket Sort):首先将元素分在不同的桶中,在对每个桶中的元素排序。
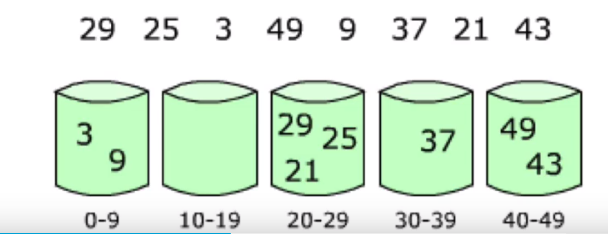
-
代码
def bucket_sort(li: list, n: int = 100, max_num: int = 10000): buckets = [[] for _ in range(n)] for var in li: i = min(var // (max_num // n), n - 1) # i表示var在第几个桶内 buckets[i].append(li[i]) for j in range(len(buckets[i]) - 1, 0, -1): if buckets[i][j] > buckets[i][j-1]: buckets[i][j], buckets[i][j-1] = buckets[i][j-1], buckets[i][j] else: break li.clear() for bucket in buckets: li.extend(bucket) -
桶排序的表现取决于数据的分布。也就是需要对不同数据排序时采取不同的分桶策略。
-
平均情况时间复杂度:O(n+k)
-
最坏情况时间复杂度:O(n2k)
-
空间复杂度:O(nk)
十一、基数排序
-
多关键字排序:加入现在有一个员工表,要求按照薪资排序,薪资相同的员工按照年龄排序。
-
先按照年龄进行排序,再按照薪资进行稳定的排序。
-
-
对32,12,94,52,17,54,93排序,是否可以看做多关键字排序?
-
代码
def radix_sort(li: list): """ 基数排序 :param li: :return: """ it, max_num = 0, max(li) while 10 ** it <= max_num: buckets = [[] for _ in range(10)] for var in li: # it=0 098 // 1 % 10-> 7 it=1 987 987 //10->98 98%10->8 it=2 987 // 100 -> 9 9%10-> 9 digit = (var // 10 ** it) % 10 buckets[digit].append(var) # 分桶完成 li.clear() # 把数重新写回li for bucket in buckets: li.extend(bucket) it += 1 -
时间复杂度:O(kn)
-
空间复杂度:O(k+n)
-
k表示数字位数
查找
一、顺序查找
-
-
代码
def linear_search(li, val): for i, v in enumerate(li): if v == val: return i return None -
二、二分查找
-
看似简单,写对很难
-
变形很多
-
在⾯试中常⽤来考察code能⼒
-
定义
⼆分搜索也称折半搜索,是⼀种在有序数组中查找某⼀特定元素的搜索算法
-
运用前提
数组必须是排好序的
-
输⼊并不⼀定是数组,也可能是给定⼀个区间的起始和终⽌的位置
-
优点
⼆分搜索也称对数搜索,其时间复杂度为 O(logn),是⼀种⾮常⾼效的搜索
-
缺点
要求待查找的数组或区间是排好序的
若要求对数组进⾏动态地删除和插⼊操作并完成查找,平均复杂度会变为 O(n)
采取⾃平衡的⼆叉查找树
可在 O(nlogn) 的时间内⽤给定的数据构建出⼀棵⼆叉查找树
可在 O(logn) 的时间内对数据进⾏搜索
可在 O(logn) 的时间内完成删除和插⼊的操作
当:输⼊的数组或区间是有序的,且不会常变动,要求从中找出⼀个满⾜条件的元素 采⽤⼆分搜索
-
代码实现
def binary_search(alist,item):
"""二分查找"""
n = len(alist)
if n > 0:
mid = n//2
if alist[mid] == item:
return True
elif item < alist[mid]:
return binary_search(alist[:mid],item)
else:
return binary_search(alist[mid+1:],item)
return False
def binary_search_2(alist,item):
"""二分查找非递归查版本"""
n = len(alist)
first = 0
last = n-1
while first <= last:
mid = (first + last) // 2
if alist[mid] == item:
return True
elif item < alist[mid]:
last = mid - 1
else:
first = mid + 1
return False
def binary_search2(li, val):
left, right = 0, len(li) - 1
while left <= right: # 候选区有值
mid = (left + right) // 2
if li[mid] == val:
return mid
elif li[mid] > val: # 待查找的值在mid的左侧
right = mid -1
else: # li[mid] < val 待查找的值在mid右侧
left = mid + 1
return None
if __name__ == '__main__':
li = [17, 20, 31, 44, 54, 55, 77, 93, 226]
# print(binary_search(li,31))
# print(binary_search_2(li,31))
print(binary_search2(li=li, val=44))
三、查找排序相关算法题
1. 给两个字符串s和t,判断t是否为s的重新排列后组成的单词
-
s = 'anagram',t = 'nagaram',return true
-
s = 'rat', t = 'car', return false.
-
代码
 字符串判断
字符串判断class Solution: def isAnagram(self, s: str, t: str) -> bool: dict1, dict2 = {}, {} for i in s: dict1[i] = dict1.get(i, 0) + 1 for j in t: dict2[j] = dict2.get(j, 0) + 1 return dict1 == dict2 # return sorted(list(s)) == sorted(list(t))
2. 给定一个m*n的二维列表,查找一个数是否存在。列表有下列特性:
-
每一行的列表从左到右已经排序好。
-
每一行第一个数比上一行最后一个数大。
[
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
] -
代码
-
线性查找
 线性查找
线性查找class Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: for line in matrix: if target in line: return True return False
-
二分查找
 二分查找
二分查找class Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: h = len(matrix) if h == 0: return False w = len(matrix[0]) if w == 0: return False left, right = 0, w * h -1 while left <= right: mid = (left + right) // 2 i, j = mid // w, mid % w if matrix[i][j] == target: return True elif matrix[i][j] > target: right = mid - 1 else: left = mid + 1 else: return False
-
3. 给定一个列表和一个整数,设计算法找到两个数的下标,使得两个数之和为给定的整数。保证肯定仅有一个结果。
-
例如,列表[1,2,5,4]与目标整数3,1+2=3,结果为(0, 1).
-
思路1:先对列表排序,然后循环列表元素,采用二分查找法查找target-当前位置元素的值是否在列表中,并返回其下标
-
代码
 两数之和
两数之和class Solution: def binary_search(self, li, left, right, val) -> int: while left <= right: mid = (left + right) // 2 if li[mid][0] == val: return mid elif li[mid][0] > val: right = mid - 1 else: left = mid + 1 return def twoSum(self, nums: list, target: int) -> list: new_nums = [[num, i] for i, num in enumerate(nums)] new_nums.sort(key=lambda x: x[0]) for i in range(len(new_nums)): a = new_nums[i][0] b = target - a j = self.binary_search(new_nums, i + 1, len(new_nums) - 1, b) if j: break return sorted([new_nums[i][1], new_nums[j][1]])
4. leetcode-167两数之和-有序数组
- 代码

class Solution: def binary_search(self, li, left, right, val): while left <= right: mid = (left + right) // 2 if li[mid] == val: return mid elif li[mid] < val: left = mid + 1 else: right = mid - 1 return def twoSum(self, numbers: List[int], target: int) -> List[int]: for i in range(len(numbers)): a = numbers[i] b = target - a if b >= a: j = self.binary_search(numbers, i + 1, len(numbers)-1, b) else: j = self.binary_search(numbers, 0, i - 1, b) if j: break return sorted([i + 1, j + 1])
递归
-
把⼤规模的问题不断地变⼩,再进⾏推导的过程
-
递归算法是⼀种调⽤⾃身函数的算法
-
特点:可以使⼀个看似复杂的问题变得简洁和易于理解
-
经典案例:汉诺塔(⼜称河内塔)
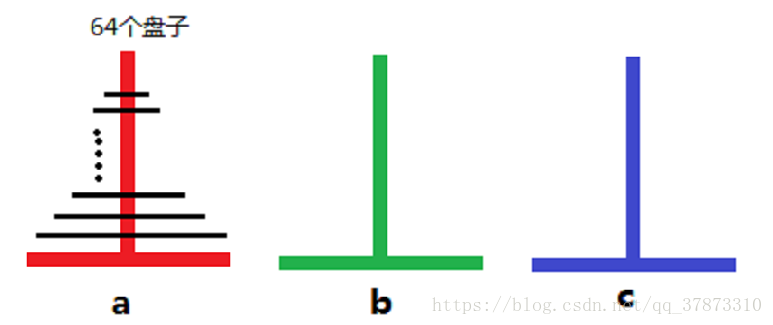
汉诺塔问题是一个经典的问题。汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
-
解决思路
n个盘子时
1 .把n-1个盘子从A经过C移动到B
2. 把第n个圆盘从A移动到C
3. 把N-1个小圆盘从B经过A移动到C -
代码
def hanoi(n, a, b, c): if n > 0: hanoi(n-1, a, c, b) print(f"moving from {a} to {c}") hanoi(n-1, b, a, c) -
汉诺塔移动次数的递推式:h(x) = 2h(x-1) + 1
-
h(64) = 18446744073709551615
-
假设婆罗门每秒钟搬一个盘子,则总共需要5800亿年。
-
-
算法思想
-
要懂得如何将⼀个问题的规模变⼩
-
再利⽤从⼩规模问题中得出的结果
-
结合当前的值或者情况,得出最终的结果
-
-
通俗理解 ⾃顶向下(Top-Down)
-
把要实现的递归函数,看成已经实现好的
-
直接利⽤解决⼀些⼦问题
-
思考:如何根据⼦问题的解以及当前⾯对的情况得出答案
-
-
递归写法结构总结
function fn(n) { // 第⼀步:判断输⼊或者状态是否⾮法? if (input/state is invalid) { return; } // 第⼆步:判读递归是否应当结束? if (match condition) { return some value; } // 第三步:缩⼩问题规模 result1 = fn(n1) result2 = fn(n2) ... // 第四步: 整合结果 return combine(result1, result2) }判断当前情况是否⾮法,如果⾮法就⽴即返回,
也称为完整性检查(Sanity Check)
‣ 判断是否满⾜结束递归的条件
‣ 将问题的规模缩⼩,递归调⽤
‣ 利⽤在⼩规模问题中的答案,结合当前的数据
进⾏整合,得出最终的答案
贪心算法
1. 定义
-
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
-
贪婪是⼀种在每⼀步选中都采取在当前状态下最好或最优的选择,从⽽希望导致结果是最好或最优的算法。
-
贪心算法并不保证会得到最优解,但是在某些问题上贪心算法的解就是最优解。要会判断一个问题能否用贪心算法来计算。
2. 找零问题
-
假设商店老板需要找零n元钱,钱币的面额有:100元、50元、20元、5元、1元,如何找零使得所需钱币的数量最少?
from collections.abc import Iterable def change(t: Iterable, n: int) -> (list, int): """ 找零问题 :param t: 纸币面额 :param n: 钱数 :return: m: list, n: int 找钱方案, 余数 """ m = [(0, 0) for _ in t] for i, money in enumerate(t): m[i] = (n // money, money) n = n % money return m, n if __name__ == '__main__': t = [100, 50, 20, 5, 1] print(change(t, 376))
3. 背包问题


def fractional_backpack(goods: list, w: int) -> (int, list):
"""
分数背包
:param goods: 商品
:param w: 重量
:return: [] 方案
"""
goods.sort(key=lambda x: x[0] / x[1], reverse=True)
m = [0 for _ in goods]
total_v = 0
for i, (prize, weight) in enumerate(goods):
if w >= weight:
m[i] = (weight, 1)
total_v += prize
w -= weight
else:
m[i] = (weight, w / weight)
total_v += m[i][1] * prize
break
return total_v, m
if __name__ == '__main__':
goods = [(60, 10), (100, 20), (120, 30)] # 每个商品元组表示(价格、重量)
print(fractional_backpack(goods=goods, w=50))
4. 拼接最大数字问题

from functools import cmp_to_key
def xy_cmp(x, y):
if x + y < y + x:
return 1
elif x + y > y + x:
return -1
else:
return 0
def number_join(li: list):
li = list(map(str, li))
li.sort(key=cmp_to_key(xy_cmp))
return "".join(li)
if __name__ == '__main__':
li = [32, 94, 128, 1286, 6, 71]
print(number_join(li=li))
5. 活动选择问题


def activity_selection(a):
res = [a[0]]
for i in range(1, len(a)):
if a[i][0] >= res[-1][1]: # 当前活动的开始时间小于等于最后一个入选活动的结束时间
res.append(a[i])
return res
if __name__ == '__main__':
activities = [(1, 4), (3, 6), (0, 6), (5, 7),(3, 9), (5, 9),(6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]
activities.sort(key=lambda x: x[1])
print(activity_selection(activities))
6. 特点
-
优点
对于⼀些问题,贪婪算法⾮常的直观有效
-
缺点
往往,它得到的结果并不是正确的 ‣ 贪婪算法容易过早地做出决定,从⽽没有办法达到最优解
7. 贪婪算法的反例



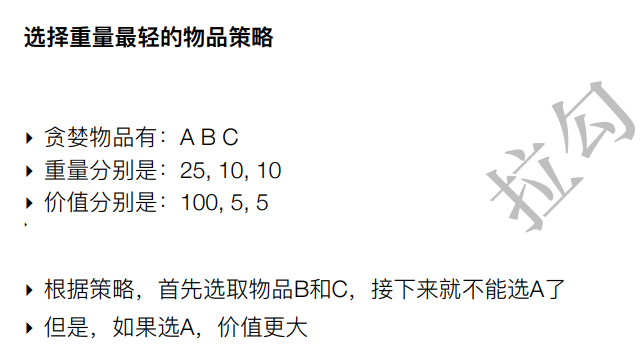
8. 贪婪的弊端
-
总是做出在当前看来是最好的选择
-
不从整体的⻆度去考虑,仅对局部的最优解感兴趣
9. 什么问题适⽤贪婪算法
-
只有当那些局部最优策略能产⽣全局最优策略的时候
动态规划
1. 从斐波那契数列看动态规划
-
斐波那契数列:Fn = Fn-1 + Fn-2
-
练习:使用递归和非递归的方法来求解斐波那契数列的第n项
-
具体实现
# 子问题的重复计算 def fabnacci_rec(n): if n == 1 or n == 2: return 1 return fabnacci_rec(n - 1) + fabnacci_rec(n - 2) # 动态规划 DP 的思想 = 最优子结构递推式 重复子问题 def fabnacci_no_rec(n): f = [0, 1, 1] if n > 2: for i in range(n - 2): num = f[-1] + f[-2] f.append(num) return f[n] if __name__ == '__main__': print(fabnacci_rec(20)) print(fabnacci_no_rec(100))
2. 基本属性
-
最优⼦结构 Optimal Substructure
-
状态转移⽅程 f(n)
-
-
重叠⼦问题 Overlapping Sub-problems
3. 钢条切割问题







-
自顶向下实现
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40] def cut_rod_recursion(p: list, n: int): """ 切割钢条 递归 :param p: :param n: :return: """ if n == 0: return 0 else: res = p[n] for i in range(1, n): res = max(res, cut_rod_recursion(p, i) + cut_rod_recursion(p, n - i)) return res def cut_rod_recursion2(p: list, n: int): if n == 0: return 0 else: res = 0 for i in range(1, n + 1): res = max(res, p[i] + cut_rod_recursion2(p, n - i)) return res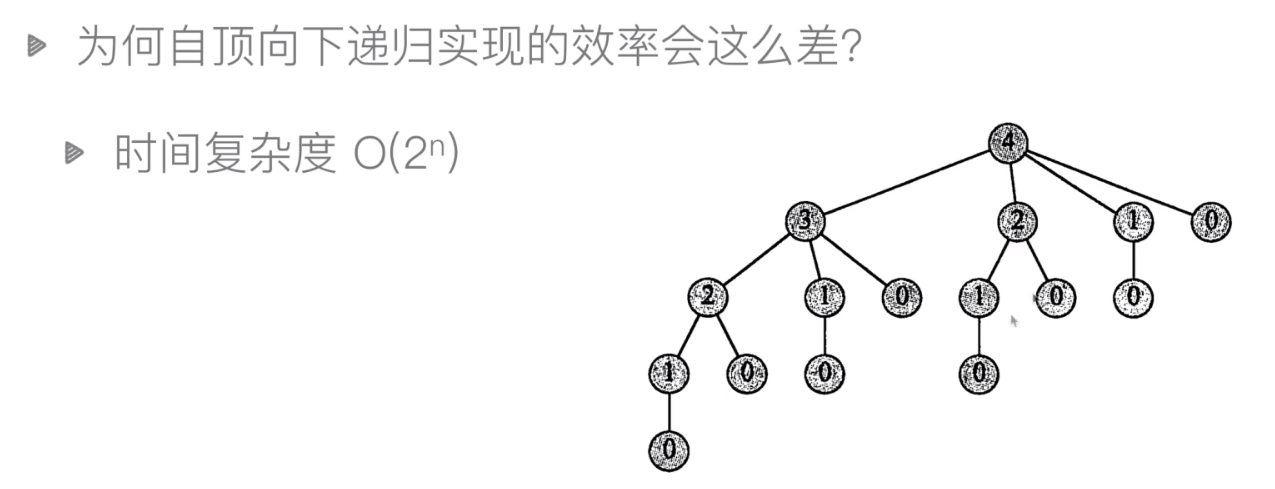
-
动态规划解法=自底向上解法


def cut_rod_dp(p: list, n: int): """ 动态规划 :param p: :param n: :return: """ r = [0] for i in range(1, n + 1): res = 0 for j in range(1, i + 1): res = max(res, p[j] + r[i - j]) r.append(res) return r[n] -
重构解

def cut_rod_extend(p, n): r, s = [0], [0] for i in range(1, n + 1): res_r = 0 # 价格的最大值 res_s = 0 # 价格最大值对应方案的左边不切割部分的长度 for j in range(1, i + 1): if p[j] + r[i -j] > res_r: res_r = p[j] + r[i -j] res_s = j r.append(res_r) s.append(res_s) return r[n], s def cut_rod_solution(p, n): r, s = cut_rod_extend(p, n) ans = [] while n > 0: ans.append(s[n]) n -= s[n] return r, ans
4. 动态规划问题关键特征
-
什么问题可以使用动态规划方法?
-
最优子结构
-
原问题的最优解中涉及多少个子问题
-
在确定最优解使用哪些子问题时,需要考虑多少种选择
-
-
重叠子问题
-
5. 最长公共子序列

-
思考:暴力穷举法的时间复杂度是多少?
-
思考:最长公共子序列是否具有最优子结构性质?


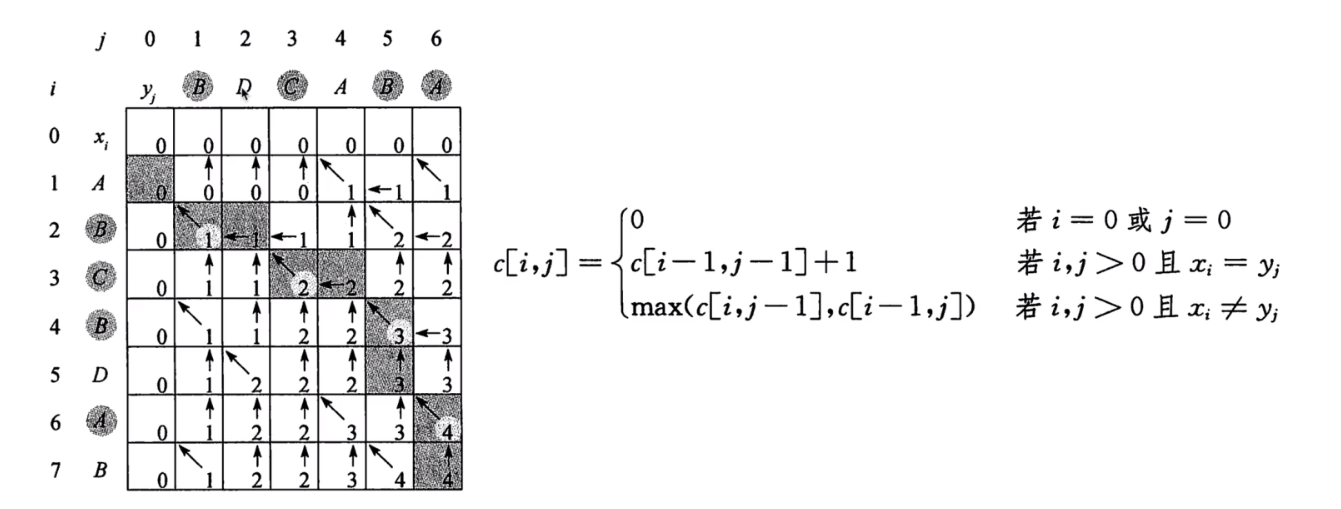
-
代码
 最长公共子序列
最长公共子序列def lcs_length(x: str, y: str): """ 最长公共子序列长度 """ m, n = len(x), len(y) c = [[0 for _ in range(n + 1)] for _ in range(m + 1)] for i in range(1, m + 1): for j in range(1, n + 1): if x[i - 1] == y[j - 1]: c[i][j] = c[i - 1][j - 1] + 1 else: c[i][j] = max(c[i][j - 1], c[i - 1][j]) for _ in c: print(_) return c[m][n] def lcs_source(x: str, y: str): """ 最长公共子序列来源 """ m, n = len(x), len(y) c = [[0 for _ in range(n + 1)] for _ in range(m + 1)] b = [[0 for _ in range(n + 1)] for _ in range(m + 1)] # b = [['↖' for _ in range(n + 1)] for _ in range(m + 1)] for i in range(1, m + 1): for j in range(1, n + 1): if x[i - 1] == y[j - 1]: c[i][j] = c[i - 1][j - 1] + 1 b[i][j] = 1 # b[i][j] = '↖' elif c[i - 1][j] >= c[i][j - 1]: c[i][j] = max(c[i][j - 1], c[i - 1][j]) b[i][j] = 2 # b[i][j] = '←' else: c[i][j] = max(c[i][j - 1], c[i - 1][j]) b[i][j] = 3 # b[i][j] = '↑' return c[m][n], b def lcs_traceback(x: str, y: str): """ 最长公共子序列回溯 """ length, b = lcs_source(x, y) i, j = len(x), len(y) res = [] while i > 0 and j > 0: if b[i][j] == 1: print(i, j) res.append(x[i - 1]) i -= 1 j -= 1 elif b[i][j] == 2: i -= 1 else: j -= 1 return ''.join(reversed(res))
欧几里得算法
1. 最大公约数
-
约数:如果整数a能被整数b整除,那么a叫做b的倍数,b叫做a的约数。
-
给定两个整数a,b,两个数的所有公共约数中的最大值即为最大公约数(Greatest Common Divisor,GCD)。
-
例:12与16的最大公约数是3
-
如何计算两个数的最大公约数:
-
欧几里得:辗转相除法(欧几里得算法)
-
《九章算术》:更相减损术

 最大公约数
最大公约数def gcd(a: int, b: int): """ 最大公约数 :param a: :param b: :return: """ if b == 0: return a return gcd(b, a % b) def gcd2(a, b): """ 最大公约数 :param a: :param b: :return: """ while b > 0: r = a % b a = b b = r print(a, b) return a
-
2. 实现分数计算
-
利用欧几里得算法实现一个分数类,支持分数的四则运算。
 分数四则运算
分数四则运算class Fraction: def __init__(self, a, b): self.a = a self.b = b x = self.gcd(a, b) self.a /= x self.b /= x def gcd(self, a, b): """ 最大公约数 :param a: :param b: :return: """ while b > 0: r = a % b a = b b = r return a def __str__(self): return "%d/%d"%(self.a, self.b) def zgs(self, a, b): """ 最大公倍数 :param a: :param b: :return: """ x = self.gcd(a, b) return a * b / x def __add__(self, other): """ 加法 :param other: :return: """ a = self.a b = self.b c = other.a d = other.b deno = self.zgs(b, d) elem = a * deno / b + c * deno / d return Fraction(elem, deno) def __sub__(self, other): """ 减法 """ a = self.a b = self.b c = other.a d = other.b deno = self.zgs(b, d) elem = a * deno / b - c * deno / d return Fraction(elem, deno) def __mul__(self, other): """ 乘法 """ return Fraction(self.a * other.a, self.b * other.b) def __truediv__(self, other): """ 除法 """ return Fraction(self.a * other.b, self.b * other.a) if __name__ == '__main__': print(Fraction(12, 16)) a = Fraction(1, 3) b = Fraction(1, 2) print(a, b) print(a + b) print(a - b) print(a * b) print(a / b)
RSA加密算法
-
密码与加密
-
传统密码:加密算法是秘密的
-
现代密码系统:加密算法是公开的,密钥是秘密的
-
对称加密
-
非对称加密
-
-
RSA非对称加密系统:
-
公钥:用来加密,是公开的
-
私钥:用来解密,是私有的
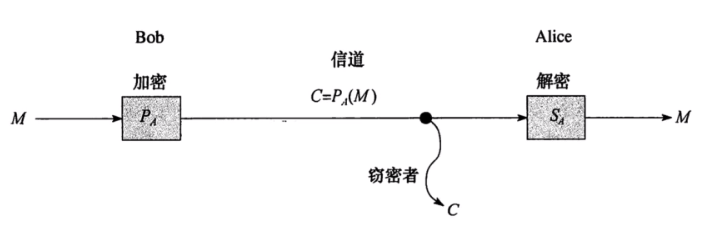
-
-
RSA加密算法过程


-
代码
In [1]: p = 53 In [2]: q = 59 In [3]: n = p * q In [4]: fai = (p - 1) * (q - 1) In [5]: e = 3 In [6]: d = 2011 In [7]: (e * d) % fai Out[7]: 1 In [8]: m = 87 In [9]: c = (m ** e) % n In [10]: (c ** d) % n Out[10]: 87 In [11]: m = 56 In [12]: c = (m ** e) % n In [13]: (c ** d) % n Out[13]: 56
-
-