数据结构与算法系列(一)-- 数据结构
本节目录
基础数据结构
-
- 1、列表/数组
- 2、链表
- 3、哈希表
- 4、跳表
- 5、栈
- 6、队列
- 7、树
高级数据结构
- 1、优先队列
- 2、图
- 3、前缀树
- 4、线段树
- 5、树状数组
什么是数据结构?
-
-
简单来说,数据结构就是设计数据以何种方式组织并存储在计算机中。
-
比如:列表、集合与字典等都是一种数据结构。
-
N.Wirth:程序=数据结构+算法
-
数据结构分为逻辑结构和物理结构
-
数据结构按照其逻辑结构可分为线性结构、树结构、图结构
-
线性结构:数据结构中的元素存在一对一的相互关系
-
树结构:数据结构中的元素存在一对多的相互关系
-
-
基础数据结构
一、 列表/数组





-
-
列表与数据有两点不同:
-
数组元素类型要相同
-
数组长度固定
-
-
关于列表的问题:
-
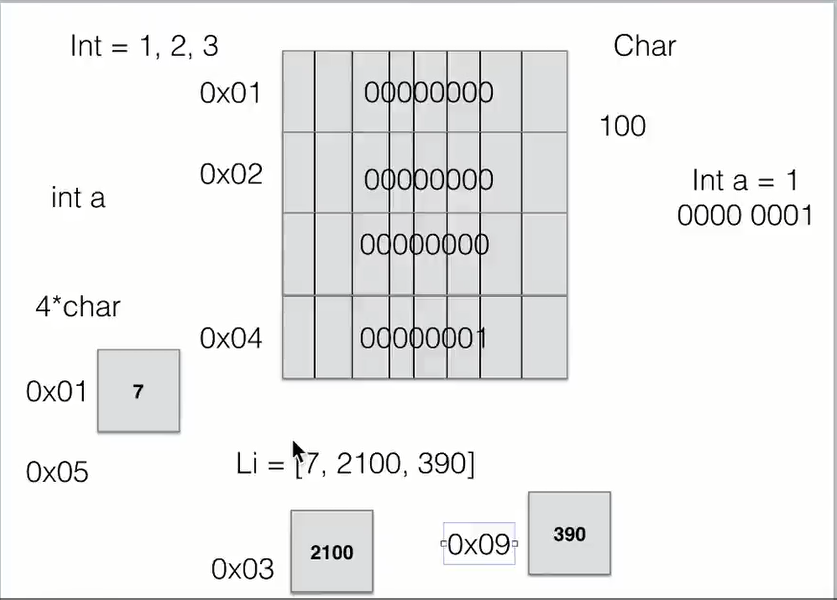
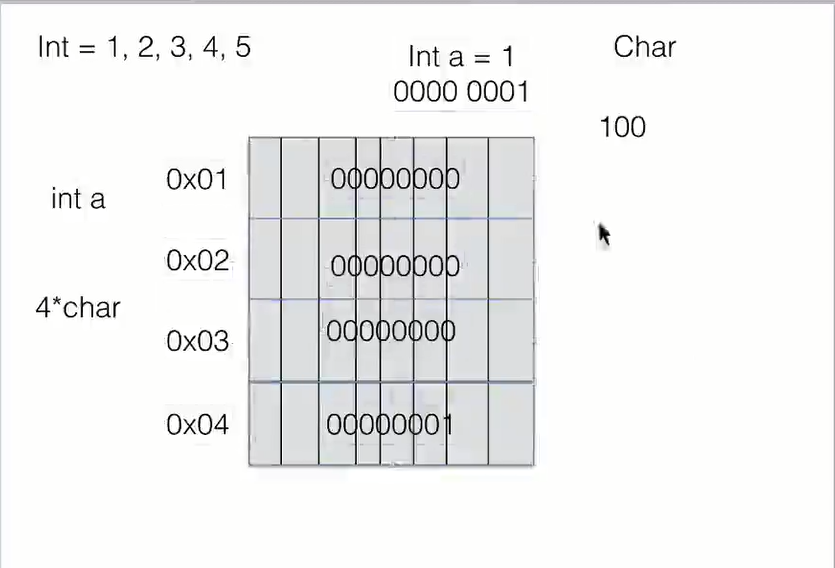
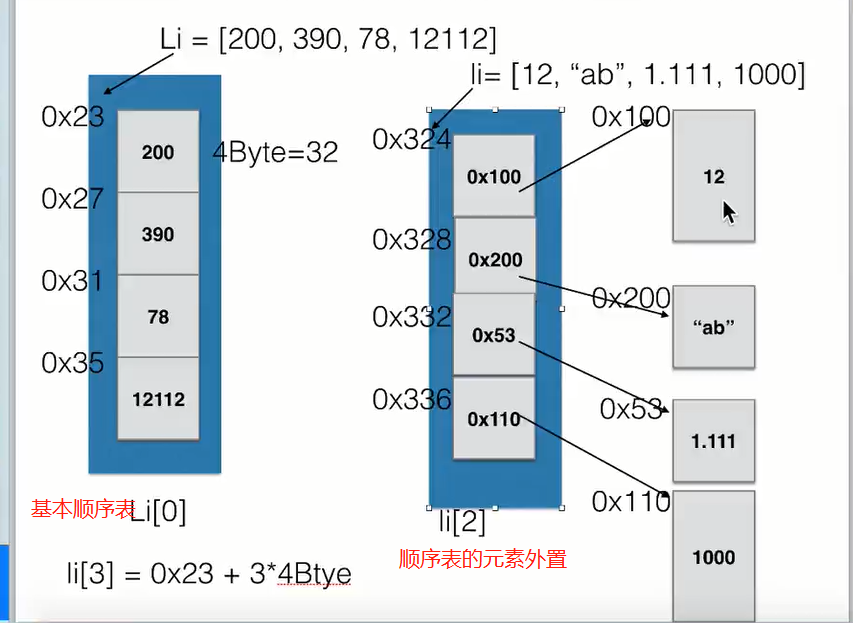
列表中的元素是如何存储的?存储元素的地址以实现存储不同类型的数据元素,每次添加会动态开辟一块新的内存以实现数组长度固定的问题。
-
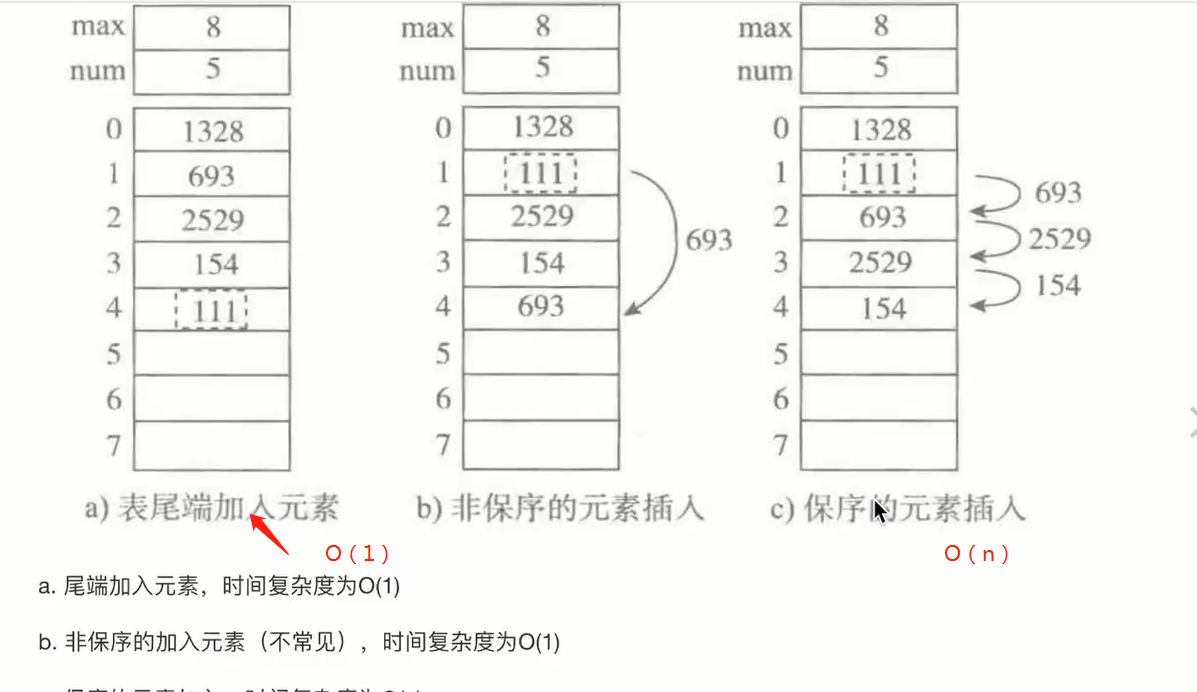
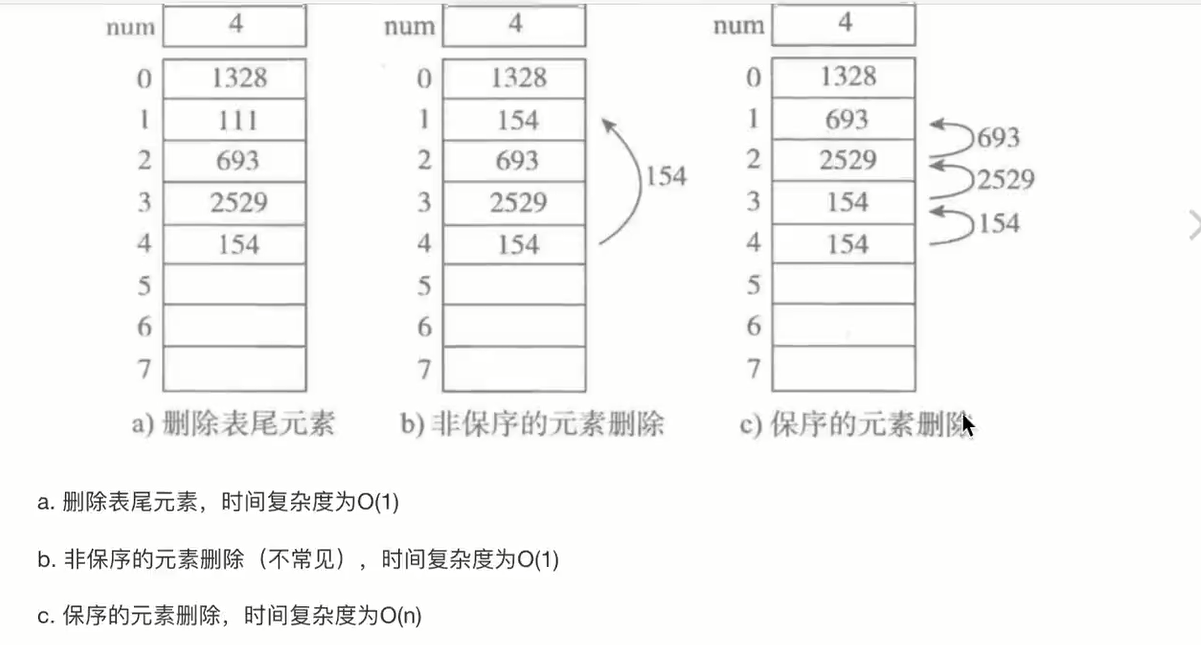
列表的基本操作:按下标查找、插入元素、删除元素.....
-
这些操作的时间复杂度是多少?按下标查找和append为O(1),前插、中间插入和删除为O(n)
-
-
扩展:Python的列表是如何实现的?
-
Array
-
java,C++: int a[100]
-
Python: a = [1,2,3]
-
javascript: let a = [1,2,3]
-
Go: a []int{1,2,3}
-
| 操作 | 数组 | 链表 |
|---|---|---|
| prepend | O(n)/O(1) | O(1) |
| append | O(1) | O(1) |
| lookup | O(1) | O(n) |
| insert | O(n) | O(1) |
| delete | O(n) | O(1) |
-
优点
构建⼀个数组⾮常简单
能让我们在 O(1) 的时间⾥根据数组的下标(index)查询某个元素
-
缺点
构建时必须分配⼀段连续的空间
查询某个元素是否存在时需要遍历整个数组,耗费 O(n) 的时间(其中,n 是元素的个数)
删除和添加某个元素时,同样需要耗费 O(n) 的时间
链表(Linked List)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。

由于不必须按顺序存储,链表在插入的时候可以达到 O(1)的复杂度,比另一种线性表 —— 顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要 O(n)的时间,而顺序表相应的时间复杂度分别是 O(log\ n)和 O(1)。使用链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。在计算机科学中,链表作为一种基础的数据结构可以用来生成其它类型的数据结构。链表通常由一连串节点组成,每个节点包含任意的实例数据(data fields)和一或两个用来指向上一个/或下一个节点的位置的链接(links)。链表最明显的好处就是,常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序,数据的访问往往要在不同的排列顺序中转换。而链表是一种自我指示数据类型,因为它包含指向另一个相同类型的数据的指针(链接)。
链表允许插入和移除表上任意位置上的节点,但是不允许随机存取。链表有很多种不同的类型:单向链表,双向链表以及循环链表。链表通常可以衍生出循环链表,静态链表,双链表等。对于链表使用,需要注意头结点的使用。
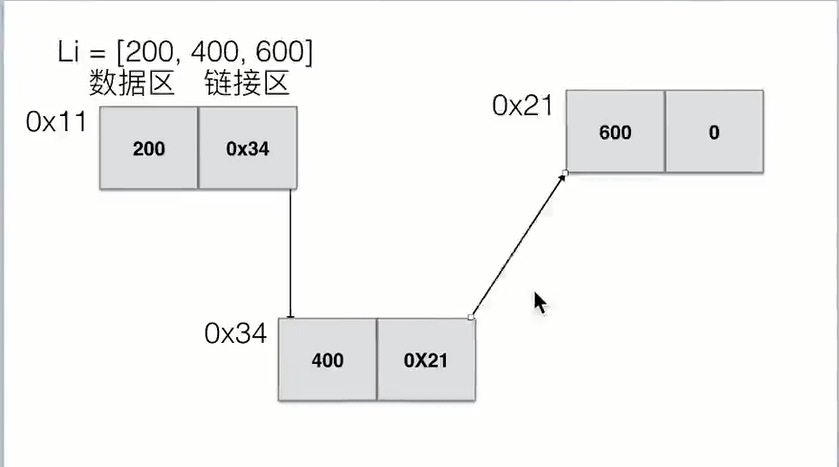
- 链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是不像顺序表一样连续存储数据,而是在每一个节点(数据存储单元)里存放下一个节点的位置信息(即地址)。
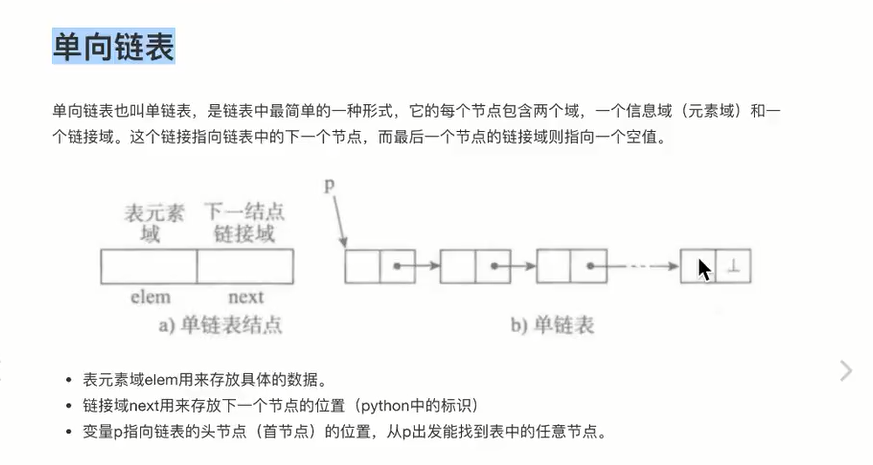
- 单向链表:也叫单链表,是链表中最简单的一种形式。链表中的每个元素实际上是⼀个单独的对象,⽽所有对象都通过每个元素中的引⽤字段链接在⼀起。它的每个节点包含两个域,一个信息域(元素域),一个链接域。这个链接指向链表中的下一个结点,而最后一个节点的链接则指向一个空值。表元素域elem用来存放具体的数据,链接域next用来存放下一个节点的位置(python中的标识),变量p指向链表的头结点(首节点)的位置,从p出发能找到表中的任意节点。
- 双向链表:与单链表不同的是,双链表的每个结点中都含有 两个引⽤字段,一个指向前一个节点(前驱),一个指向后一个节点(后继)。当此节点为第一个节点时,前驱为空,当此节点为尾节点时,后继为空。
链表的存储方式
2.1 单链表
- 单链表的操作

-
链表是由一系列节点组成的元素集合。每个节点包含两部分,数据域item和指向下一个节点的指针next。通过节点之间的相互连接,最终串联成一个链表。
class Node(object): def __init__(self, item): self.item = item self.next = None
- 头插法
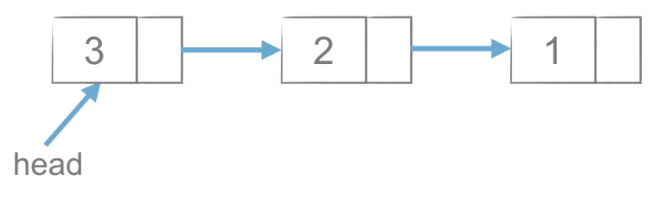
- 代码
def create_linklist_head(li: list):
"""
头插法创建链表
:param li:
:return:
"""
head = Node(li[0])
for elem in li[1:]:
node = Node(elem)
node.next = head
head = node
return head
def add(self,item):
"""链表头部添加元素,头插法"""
node = Node(item)
node.next = self.__head
self.__head = node
-
尾插法
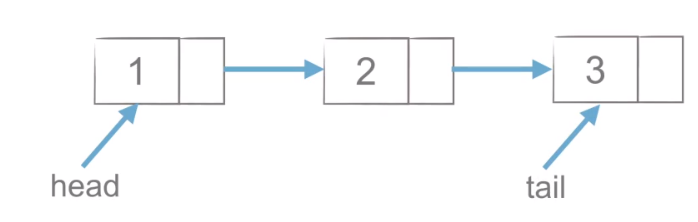
-
代码
def create_linklist_tail(li: list): """ 创建链表:尾插法 :param li: :return: """ head = Node(li[0]) tail = head for elem in li[1:]: node = Node(elem=elem) tail.next = node tail = tail.next return head def append(self,item): """链表尾部添加元素,尾插法""" node = Node(item) if self.is_empty():#链表判空 self.__head = node else: cur = self.__head while cur.next: cur = cur.next cur.next = node
-
-
链表节点之间插入
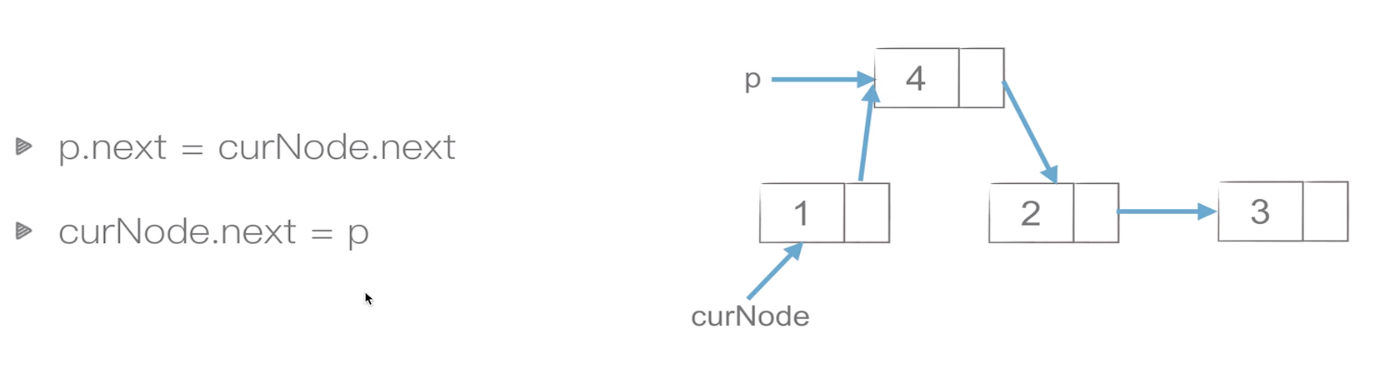
-
代码
def insert(self,pos,item): #insert(2,100) """指定位置添加元素 :param pos 从0开始 """ if pos<=0: self.add(item) elif pos>(self.length()-1): self.append(item) else: node = Node(item) pre = self.__head count = 0 while count < pos-1: pre = pre.next count += 1 #当循环退出后,pre指向pos-1位置 node.next = pre.next pre.next = node -
-
链表节点的删除

-
代码
def remove(self, item): """删除节点""" cur = self.__head prev = None while cur: if cur.elem == item: # 先判断此节点是否是头结点 if cur == self.__head: self.__head = cur.next else: prev.next = cur.next break else: prev = cur cur = cur.next
-
-
链表的遍历
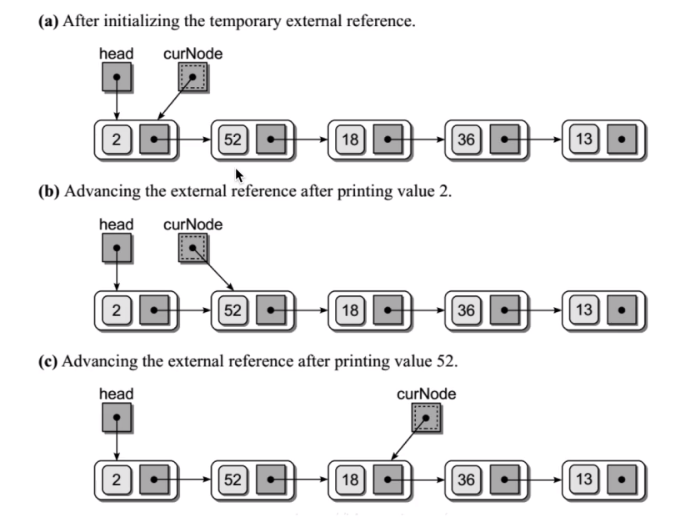
-
代码
def print_linklist(head: Node): """ 遍历列表 :param head: :return: """ while head: if head.next: print(head.elem, end='->') else: print(head.elem) head = head.next def travel(self): """遍历整个链表""" cur = self.__head while cur: if cur.next: print(cur.elem,end="->") else: print(cur.elem) cur = cur.next
-
-
单链表代码示例
 单链表示例
单链表示例class Node(object): """节点""" def __init__(self, elem): self.elem = elem self.next = None class SingleLinkList(object): """单链表""" def __init__(self, node=None): self.__head = node def __str__(self): if not self.__head: return 'None' else: cur = self.__head list_str = '' while cur: cur_str = '{}->'.format(cur.elem) if cur.next else str(cur.elem) list_str += cur_str cur = cur.next return list_str def is_empty(self): """链表是否为空""" return self.__head is None def length(self): """链表长度""" # cur游标,用来移动遍历节点 cur = self.__head # count记录数量 count = 0 while cur: # cur.next == None cur = cur.next count += 1 return count def travel(self): """遍历整个链表""" cur = self.__head while cur: if cur.next: print(cur.elem, end="->") else: print(cur.elem) cur = cur.next def add(self, item): """链表头部添加元素,头插法""" node = Node(item) node.next = self.__head self.__head = node def append(self, item): """链表尾部添加元素,尾插法""" node = Node(item) if self.is_empty(): # 链表判空 self.__head = node else: cur = self.__head while cur.next: cur = cur.next cur.next = node def insert(self, pos, item): # insert(2,100) """指定位置添加元素 :param pos 从0开始 """ if pos <= 0: self.add(item) elif pos > (self.length() - 1): self.append(item) else: node = Node(item) pre = self.__head count = 0 while count < pos - 1: pre = pre.next count += 1 # 当循环退出后,pre指向pos-1位置 node.next = pre.next pre.next = node def remove(self, item): """删除节点""" cur = self.__head prev = None while cur: if cur.elem == item: # 先判断此节点是否是头结点 if cur == self.__head: self.__head = cur.next else: prev.next = cur.next break else: prev = cur cur = cur.next def search(self, item): """查询节点是否存在""" cur = self.__head while cur: if cur.elem == item: return True cur = cur.next return False def index(self, item): """查询节点是否存在""" cur = self.__head count = 0 while cur: if cur.elem == item: return count cur = cur.next count += 1 return '{} is not in linklist'.format(item) def value(self, index): """查找指定位置的值""" if self.is_empty(): return None elif index > self.length() - 1: return 'linklist index out of range' cur = self.__head count = 0 while count < index: count += 1 cur = cur.next return cur.elem
2.2 双链表
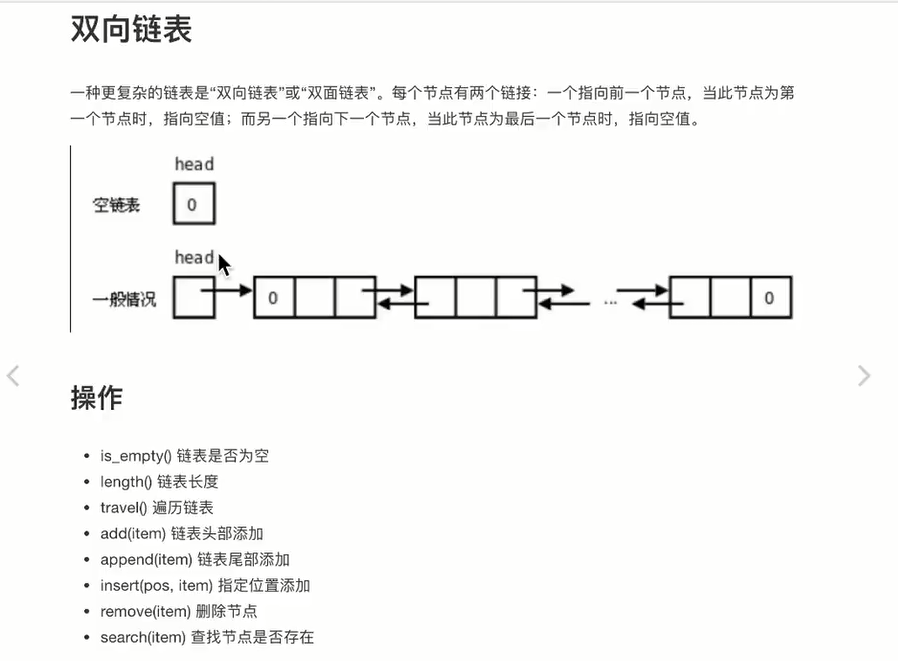
-
双链表的每个节点有两个指针:一个指向后一个节点,另一个指向前一个节点。
class Node(object): def __init__(self,item): self.item = item self.prior = None self.next = None -
如何建立双链表?
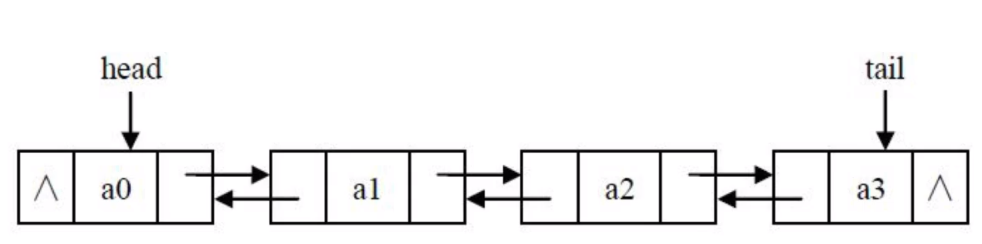
-
双链表节点的插入
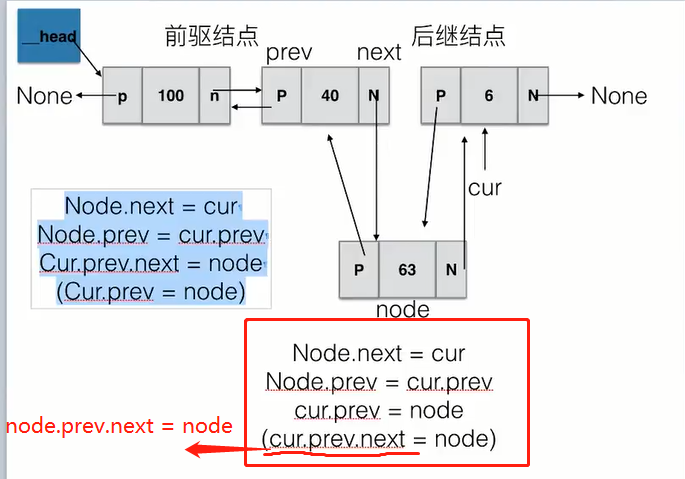

-
双链表节点的删除
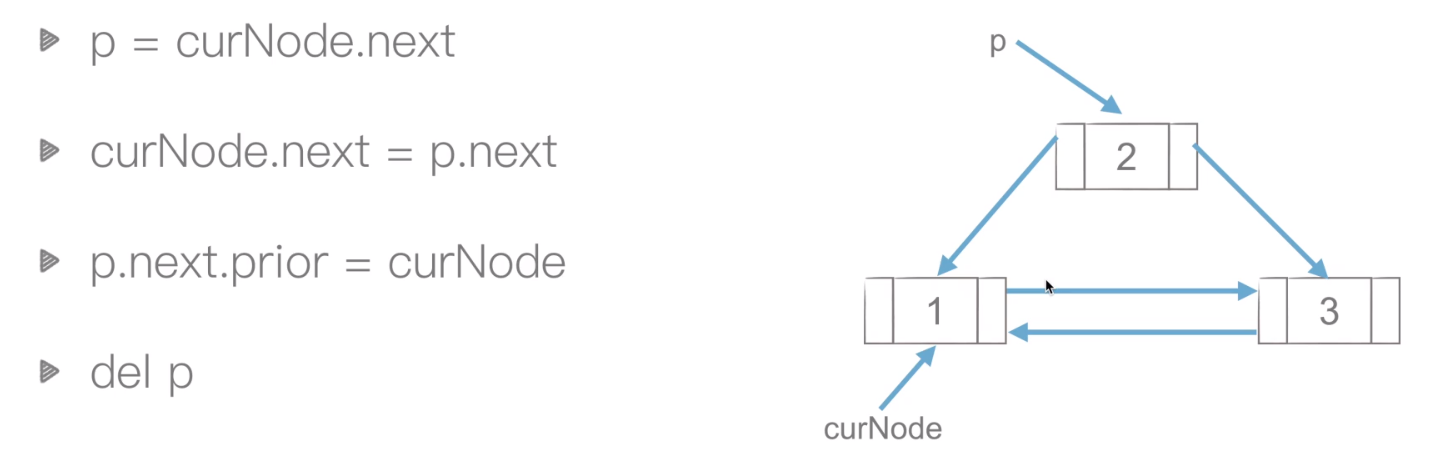
-
代码示例
 双链表示例
双链表示例class Node(object): """结点""" def __init__(self,item): self.elem = item self.prev = None self.next = None class DoubleLinkList(object): """双链表""" def __init__(self,node=None):#默认为None第一次创建空链表 self.__head = node def __str__(self): self.travel() return def is_empty(self): """链表是否为空""" return self.__head is None def length(self): """链表长度""" #cur游标,用来移动遍历节点 cur = self.__head #count记录数量 count = 0 while cur: #cur.next == None cur = cur.next count += 1 return count def travel(self): """遍历整个链表""" cur = self.__head while cur: print(cur.elem,end=" ") cur = cur.next print('') def add(self,item): """链表头部添加元素,头插法""" node = Node(item) node.next = self.__head self.__head = node node.prev = None def append(self,item): """链表尾部添加元素,尾插法""" node = Node(item) if self.is_empty():#链表判空 self.__head = node else: cur = self.__head while cur.next: cur = cur.next cur.next = node node.prev = cur def insert(self,pos,item): #insert(2,100) """指定位置添加元素 :param pos 从0开始 """ if pos<=0: self.add(item) elif pos>(self.length()-1): self.append(item) else: cur = self.__head count = 0 while count < pos: cur = cur.next count += 1 #当循环退出后,pre指向pos-1位置 node = Node(item) node.next = cur node.prev = cur.prev cur.prev.next = node cur.prev = node def remove(self,item): """删除节点""" if self.is_empty(): return cur = self.__head while cur: if cur.elem == item: #先判断此节点是否是头结点 if cur == self.__head: self.__head = cur.next if cur.next: #判断链表是否只有一个节点 cur.next.prev = None else: cur.prev.next = cur.next if cur.next: #判断链表是否是尾节点 cur.next.prev = cur.prev break else: cur = cur.next def search(self,item): """查询节点是否存在""" cur = self.__head while cur: if cur.elem == item: return True cur = cur.next return False def index(self,item): """查询节点是否存在""" cur = self.__head count = 0 while cur: if cur.elem == item: return count cur = cur.next count += 1 return '{} is not in linklist'.format(item) def value(self,index): """查找指定位置的值""" if self.is_empty(): return None elif index>self.length()-1: return 'linklist index out of range' cur = self.__head count = 0 while count<index: count += 1 cur = cur.next return cur.elem
2.3 循环列表
-
单向循环列表
-
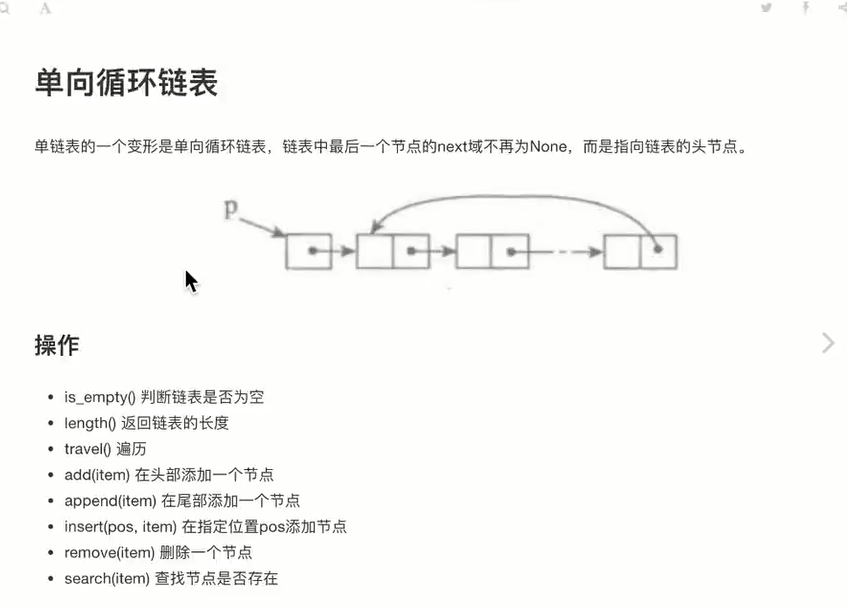
 单向循环链表
单向循环链表class Node(object): """节点""" def __init__(self, elem): self.elem = elem self.next = None class SingleCycleLinkList(object): """单向循环链表""" def __init__(self, node=None): self.__head = node if node: node.next = node def __str__(self): if not self.__head: return 'None' else: cur = self.__head list_str = '' while cur: cur_str = '{}->'.format(cur.elem) if cur.next else str(cur.elem) list_str += cur_str cur = cur.next return list_str def is_empty(self): """链表是否为空""" return self.__head is None def length(self): """链表长度""" #cur游标,用来移动遍历节点 if self.is_empty(): return 0 cur = self.__head #count记录数量 count = 1 while cur.next != self.__head: #cur.next == None cur = cur.next count += 1 return count def travel(self): """遍历整个链表""" if self.is_empty(): return cur = self.__head while cur.next != self.__head: print(cur.elem,end=" ") cur = cur.next #退出循环,cur指向尾节点,但尾节点的元素未打印 print(cur.elem) def add(self,item): """链表头部添加元素,头插法""" node = Node(item) if self.is_empty(): self.__head = node node.next = node else: cur = self.__head while cur.next != self.__head: cur = cur.next node.next = self.__head self.__head = node # cur.next = node cur.next = self.__head def append(self,item): """链表尾部添加元素,尾插法""" node = Node(item) if self.is_empty():#链表判空 self.__head = node node.next = node else: cur = self.__head while cur.next != self.__head: cur = cur.next node.next = cur.next cur.next = node def insert(self,pos,item): #insert(2,100) """指定位置添加元素 :param pos 从0开始 """ if pos<=0: self.add(item) elif pos>(self.length()-1): self.append(item) else: node = Node(item) pre = self.__head count = 0 while count < pos-1: pre = pre.next count += 1 #当循环退出后,pre指向pos-1位置 node.next = pre.next pre.next = node def remove(self,item): """删除节点""" if self.is_empty(): return cur = self.__head prev = None while cur.next != self.__head: if cur.elem== item: #先判断此节点是否是头结点 if cur == self.__head: #头结点的情况 #找尾节点 rear = self.__head while rear.next != self.__head: rear = rear.next self.__head = cur.next rear.next = self.__head else: #中间节点 prev.next = cur.next return else: prev = cur cur = cur.next #退出循环,cur指向尾节点 if cur.elem == item: if cur == self.__head: #链表中只有一个节点 self.__head = None else: # prev.next = cur.next prev.next = self.__head def search(self,item): """查询节点是否存在""" if self.is_empty(): return False cur = self.__head while cur.next != self.__head: if cur.elem == item: return True cur = cur.next #退出循环,cur指向尾节点 if cur.elem == item: return True return False def index(self,item): """查询节点是否存在""" if self.is_empty(): return None cur = self.__head count = 0 while cur.next != self.__head: if cur.elem == item: return count cur = cur.next count += 1 if cur.elem == item: return count raise ValueError('{} is not in linkCyclelist'.format(item)) def value(self,index): """查找指定位置的值""" if self.is_empty(): raise AttributeError('LinkCycleList is None') elif index>self.length()-1: raise IndexError('linklist index out of range') cur = self.__head count = 0 while count<index: count += 1 cur = cur.next return cur.elem if __name__ == '__main__': ll = SingleCycleLinkList() print(ll.is_empty()) print(ll.length()) # print(ll) ll.append(1) print(ll.is_empty()) print(ll.length()) ll.append(2) ll.add(8) ll.append(3) ll.append(4) ll.append(5) ll.append(6) # print(ll) ll.insert(-1,9) #9,8,123456 ll.travel() ll.insert(3,100) #9,8,1,100,23456 ll.travel() ll.insert(10,200) #9,8,1,100,23456,200 ll.travel() ll.remove(9) ll.travel() ll.remove(100) ll.travel() ll.remove(200) ll.travel() print(ll.value(0)) print(ll.index(8)) # help(SingleCycleLinkList)
-
双向循环列表
-
 双向循环链表
双向循环链表class Node(object): """结点""" def __init__(self,item): self.elem = item self.prev = None self.next = None class DoubleCycleLinkList(object): """双向循环链表""" def __init__(self,node=None):#默认为None第一次创建空链表 self.__head = Node('HEAD') self.__head.next = node self.__head.prev = node if node is not None: node.next = self.__head node.prev = self.__head def __str__(self): self.travel() return def is_empty(self): """链表是否为空""" return self.__head.next is None def length(self): """链表长度""" #cur游标,用来移动遍历节点 if self.is_empty(): return 0 cur = self.__head.next #count记录数量 count = 0 while cur != self.__head: #cur.next == None cur = cur.next count += 1 return count def travel(self): """遍历整个链表""" cur = self.__head.next while cur != self.__head: print(cur.elem,end=" ") cur = cur.next print('') def add(self,item): """链表头部添加元素,头插法""" node = Node(item) if self.is_empty(): #空链表 node.next = self.__head node.prev = self.__head self.__head.next = node self.__head.prev = node else: #非空链表 node.next = self.__head.next self.__head.next = node node.prev = self.__head node.next.prev = node def append(self,item): """链表尾部添加元素,尾插法""" node = Node(item) if self.is_empty():#链表判空 node.next = self.__head node.prev = self.__head self.__head.next = node self.__head.prev = node else: cur = self.__head while cur.next != self.__head: cur = cur.next node.next = cur.next node.prev = cur cur.next = node self.__head.prev = node def insert(self,pos,item): #insert(2,100) """指定位置添加元素 :param pos 从0开始 """ if pos<=0: self.add(item) elif pos>(self.length()-1): self.append(item) else: cur = self.__head.next count = 0 while count < pos: cur = cur.next count += 1 #当循环退出后,pre指向pos-1位置 node = Node(item) node.next = cur node.prev = cur.prev cur.prev.next = node cur.prev = node def remove(self,item): """删除节点""" if self.is_empty(): return cur = self.__head.next while cur: if cur.elem == item: #先判断此节点是否是头结点 if cur == self.__head.next: self.__head.next = cur.next if cur.next == self.__head: #判断链表是否只有一个节点 self.__head.next = None self.__head.prev = None else: cur.next.prev = self.__head else: cur.prev.next = cur.next if cur.next != self.__head: #判断链表是否是尾节点 cur.next.prev = cur.prev else: self.__head.prev = cur.prev break else: cur = cur.next def search(self,item): """查询节点是否存在""" if self.is_empty(): return False cur = self.__head.next while cur: if cur.elem == item: return True cur = cur.next return False def index(self,item): """查询指定元素的索引""" cur = self.__head.next count = 0 while cur: if cur.elem == item: return count cur = cur.next count += 1 return '{} is not in linklist'.format(item) def value(self,index): """查找指定位置的值""" if self.is_empty(): return None elif index>self.length()-1: return 'linklist index out of range' cur = self.__head.next count = 0 while count<index: count += 1 cur = cur.next return cur.elem if __name__ == '__main__': dcl = DoubleCycleLinkList() print(dcl.is_empty()) print(dcl.length()) # print(dcl) dcl.append(1) print(dcl.is_empty()) print(dcl.length()) dcl.append(2) dcl.add(8) dcl.append(3) dcl.append(4) dcl.append(5) dcl.append(6) # print(dcl) dcl.insert(-1, 9) # 9,8,123456 dcl.travel() dcl.insert(3, 100) # 9,8,1,100,23456 dcl.travel() dcl.insert(10, 200) # 9,8,1,100,23456,200 dcl.travel() dcl.remove(9) dcl.travel() dcl.remove(100) dcl.travel() dcl.remove(200) dcl.travel() print(dcl.value(0)) print(dcl.index(5)) print(dcl.search(4))
2.4 复杂度分析
-
顺序表(列表/数组)与链表
-
按元素值查找,两者都是O(n)
-
按下标查找,顺序表O(1),链表O(n)
-
在某元素后插入,顺序表O(n),链表O(1)
-
删除某元素,顺序表O(n),链表O(1)
-
-
链表在插入和删除的操作上明显快于顺序表
-
链表的内存可以更灵活的分配
-
试利用链表重新实现栈和队列
-
-
链表这种链式存储的数据结构对树和图的结构有很大的启发性
2.5 顺序表和链表的对比
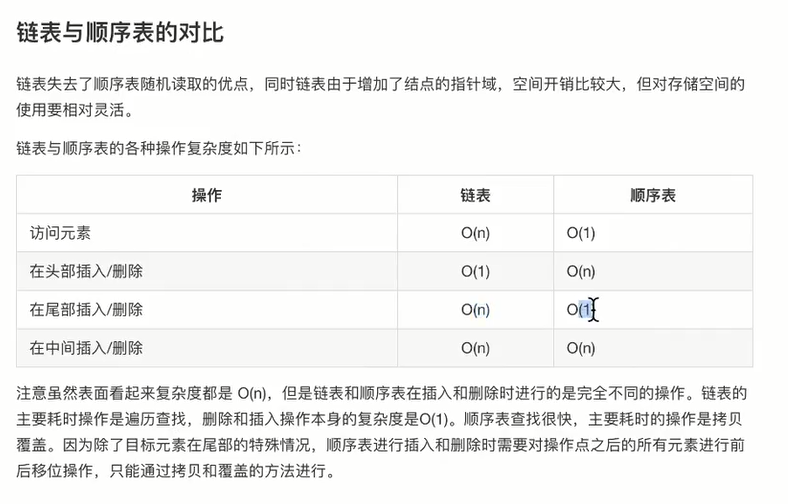
- 1. 顺序表
优点:(1) 方法简单,各种高级语言中都有数组,容易实现。
(2) 不用为表示结点间的逻辑关系而增加额外的存储开销。
(3) 顺序表具有按元素序号随机访问的特点。
缺点:(1) 在顺序表中做插入删除操作时,需要对所有元素进行前后移位操作,只能通过拷贝和覆盖的方式,平均移动大约表中一半的元素,因此对n较大的顺序表效率低。
(2) 需要预先分配足够大的存储空间,估计过大,可能会导致顺序表后部大量闲置;预先分配过小,又会造成溢出。
- 2. 链表
优点:(1) 在链表中做插入删除操作时,不会影响前面和后面的节点,因此对n较大的链表效率高(能在 O(1) 时间内删除或者添加元素)。
(2) 不需要预先分配足够大的存储空间,避免造成空间闲置或溢出的情况。(灵活地分配内存空间)
缺点:(1) 需要为表示结点间的逻辑关系(指针变量)而增加额外的存储开销。
(2) 只能通过遍历找到某个节点,不能使用下标直接定位节点(查询元素需要 O(n) 时间)。
2.6 选择合适的存储结构
- 基于存储的考虑
顺序表的存储空间是静态分配的,在程序执行之前必须明确规定它的存储规模,也就是说事先对"MAXSIZE"要有合适的设定,过大造成浪费,过小造成溢出。可见对线性表的长度或存储规模难以估计时,不宜采用顺序表;链表不用事先估计存储规模,但链表的存储密度较低。(存储密度是指一个结点中数据元素所占的存储单元和整个结点所占的存储单元之比,显然链式存储结构的存储密度是小于1的)。
- 基于运算的考虑
在顺序表中按序号访问 ai的时间性能时O(1),而链表中按序号访问的时间性能O(n),所以如果经常做的运算是按序号访问数据元素,显然顺序表优于链表;而在顺序表中做插入、删除时平均移动表中一半的元素,当数据元素的信息量较大且表较长时,这一点是不应忽视的;在链表中作插入、删除,虽然也要找插入位置,但操作主要是比较操作,从这个角度考虑显然后者优于前者。
- 基于环境的考虑
顺序表容易实现,任何高级语言中都有数组类型,链表的操作是基于指针的,相对来讲前者简单些,也是用户考虑的一个因素。
- 注:顺序表和链表抓主要用于存储,栈和队列主要用于对数据的操作。
三、哈希表
-
-
insert(key, value): 插入键值对(key, value)
-
get(key): 如果存在键为key的键值对则返回其value,否则返回空值
-
delete(key): 删除键为key的键值对
-
3.1 直接寻址表
-
直接寻址表:key为k的元素放到k位置上
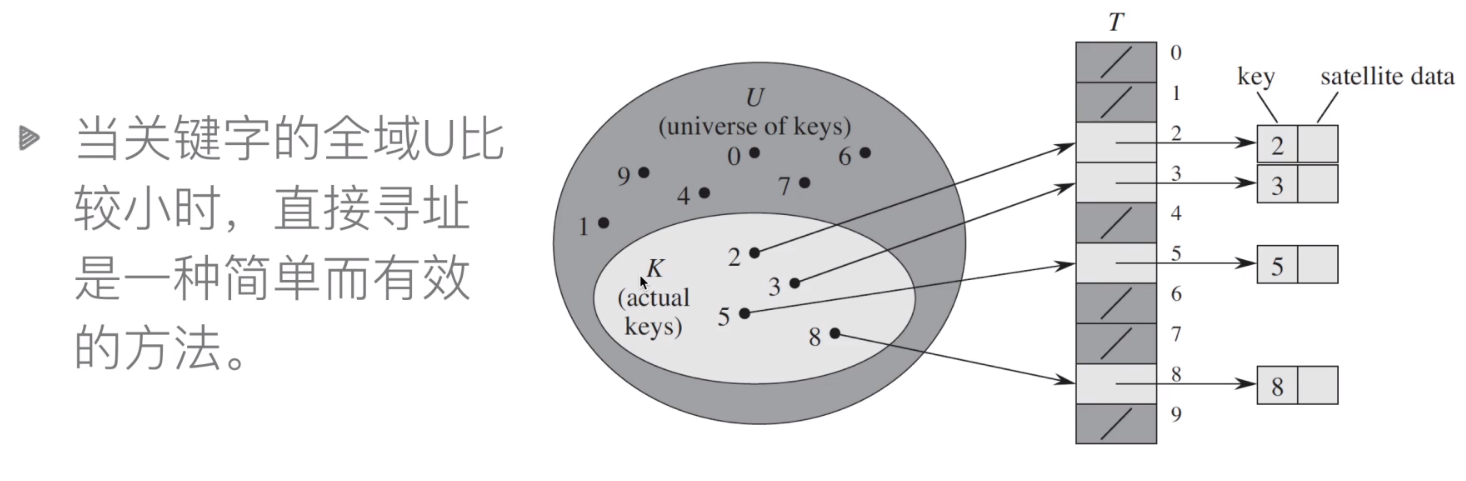
-
直接寻址技术缺点:
-
当域U很大时,需要消耗大量内存,很不实际
-
如果域U很大而实际出现的key很少,则大量空间被浪费
-
无法处理关键字不是数字的情况
-
-
改进直接寻址表:哈希(Hashing)
-
构建大小为m的寻址表T
-
key为k的元素放到h(k)位置上
-
h(k)是一个函数,其将域U映射到表T[0,1,...,m-1]
-
3.2 哈希表
-
哈希表(Hash Table,又称为散列表),是一种线性表的存储结构。哈希表由一个直接寻址表和一个哈希函数组成。哈希函数h(k)将元素关键字k作为自变量,返回元素的存储下标。
-
假设有一个长度为7的哈希表,哈希函数h(k) = k % 7。元素集合{14,22,3,5}的存储方式如下图。

-
哈希冲突
-
由于哈希表的大小是有限的,而要存储的值的总数量是无限的,因此对于任何哈希函数,都会出现两个不同元素映射到同一位置上的情况,这种情况叫做哈希冲突。
-
比如h(k)=k%7,h(0)=h(7)=h(14)=...

-
-
解决哈希冲突--开放寻址法
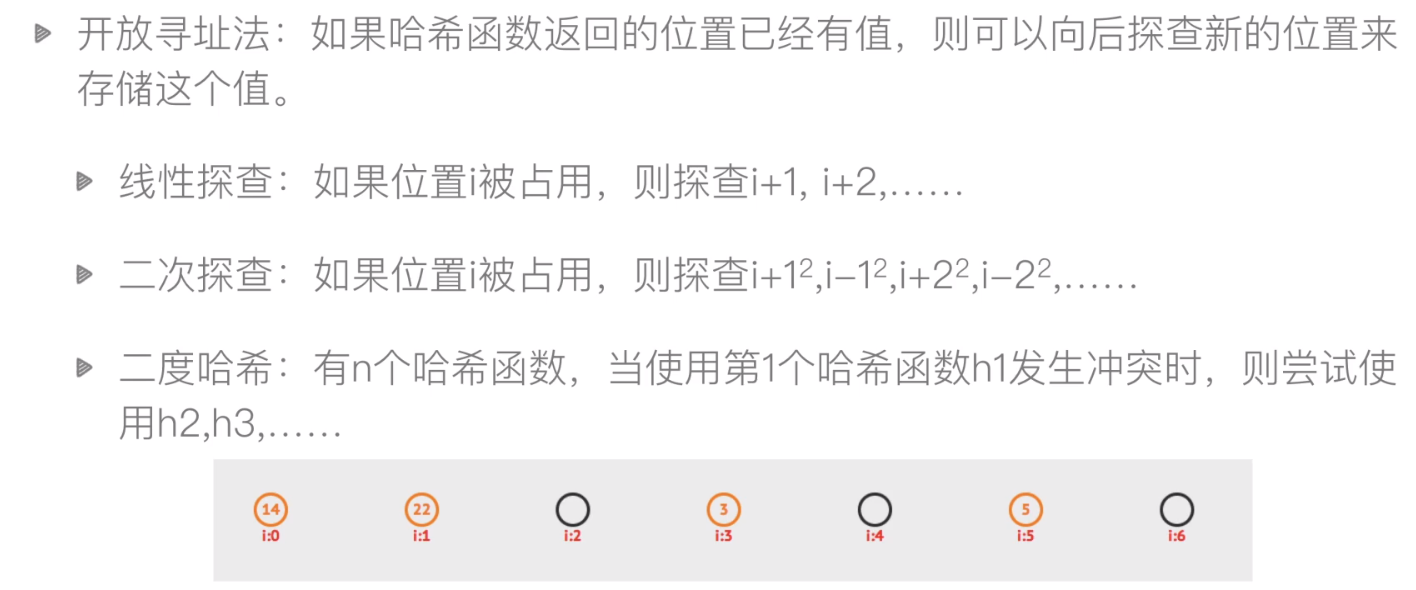
-
解决哈希冲突--拉链法

-
常见的哈希函数

-
代码示例
 哈希表示例
哈希表示例class Node: def __init__(self, item): self.item = item self.next = None class LinkListIterator: def __init__(self, node: Node): self.node = node def __next__(self): if self.node: cur_node = self.node self.node = cur_node.next return cur_node.item else: raise StopIteration def __iter__(self): return self class LinkList: def __init__(self, node: Node = None, iterable: list = None): self.head = node if node else None self.tail = None if iterable: self.extend(iterable) def extend(self, iterable: list): for elem in iterable: self.append(elem) def append(self, elem): node = Node(elem) if not self.head: self.head = node self.tail = node else: self.tail.next = node self.tail = node def find(self, elem): for item in self: if item == elem: return True else: return False def __iter__(self): return LinkListIterator(self.head) def __str__(self): return '<<' + ', '.join(map(str, self)) + '>>' class HashTable: def __init__(self, size: int = 101): self.size = size self.T = [LinkList() for _ in range(size)] def h(self, k): return k % self.size def insert(self, k): i = self.h(k) if self.find(k): print('Duplicated Insert.') else: self.T[i].append(k) def find(self, k): i = self.h(k) return self.T[i].find(k) if __name__ == '__main__': """ # li = LinkList(iterable=[1,2,3,4,5]) li = LinkList() li.append(1) li.append(2) li.append(3) li.append(4) li.append(5) for elem in li: print(elem) print(li) """ hash = HashTable() hash.insert(0) hash.insert(1) hash.insert(2) hash.insert(100) hash.insert(101) hash.insert(102) hash.insert(508) print(','.join(map(str, hash.T))) print(hash.find(103)) print(hash.find(102))
3.3 哈希表的应用
-
集合与字典

-
MD5算法


-
SHA2算法

四、跳表
链表,相信大家都不陌生,维护一个有序的链表是一件非常简单的事情,我们都知道,在一个有序的链表里面,查询跟插入的算法复杂度都是O(n)。
我们能不能进行优化呢,比如我们一次比较两个呢?那样不就可以把时间缩小一半?

同理,如果我们4个4个比,那不就更快了?

跳表时间复杂度:O(logn)
跳表空间复杂度:O(n)
思想: 升维思想 + 空间换时间
五、栈

-
-
特点:先进后出/后进先出(FILO/LIFO)
-
栈的概念:栈顶、栈底
-
栈的基本操作:
-
进栈(压栈):push
-
出栈:pop
-
取栈顶:gettop
-

-
图表示

-
算法基本思想:
可以⽤⼀个单链表来实现
只关⼼上⼀次的操作
处理完上⼀次的操作后,能在 O(1) 时间内查找到更前⼀次的操作
-
代码实现
 栈实现示例
栈实现示例class Stack(object): """栈""" def __init__(self): self.__list = [] #私有变量,不允许外部调用者对其进行操作 def push(self,item): """添加一个新的元素item到栈顶""" self.__list.append(item) #顺序表尾部插入时间复杂度O(1),头部插入O(n),故尾部方便 #self.__list.insert(0,item) #链表表尾部插入时间复杂度O(n),头部插入O(1),故链表用头插方便 def pop(self): """弹出栈顶元素""" return self.__list.pop() def peek(self): """返回栈顶元素""" if self.__list: return self.__list[-1] return None def is_empty(self): """判断栈是否为空""" return self.__list == [] # return not self.__list #0,{},[],(),'',None在python中都是False, def size(self): """返回栈的元素个数""" return self.__list.__len__() if __name__ == '__main__': s = Stack() s.push(1) s.push(2) s.push(3) s.push(4) print(s.pop()) print(s.pop()) print(s.pop()) print(s.pop())
-
栈的应用-括号匹配问题
-
括号匹配问题:给出一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。
-
例如:
()()[]{} 匹配 ([{()}]) 匹配 []( 不匹配 [(]) 不匹配 -
代码
 括号匹配
括号匹配def brace_match(s: str) -> bool: """ 栈的应用-括号匹配 括号匹配: 给出一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。 ()()[]{} 匹配 ([{()}]) 匹配 []( 不匹配 [(]) 不匹配 :return: """ match_dict = {'}': '{', ']': '[', ')': '('} stack = Stack() for ch in s: if ch in {'(', '{', '['}: stack.push(ch) elif ch in {'}', ')', ']'}: if stack.is_empty(): return False stack_top_ch = stack.pop() if stack_top_ch != match_dict[ch]: return False if stack.is_empty(): return True return False if __name__ == '__main__': # stack_test() s_list = ['[(])', '([{()}])', '[{[[[]]'] for s in s_list: print(s, brace_match(s=s))
-
六、队列
-
-
进行插入的一端称为队尾(rear),插入动作称为进队或入队
-
进行删除的一端成为队头(front),删除动作称为出队
-
特点:先进先出(First=in,First-out)
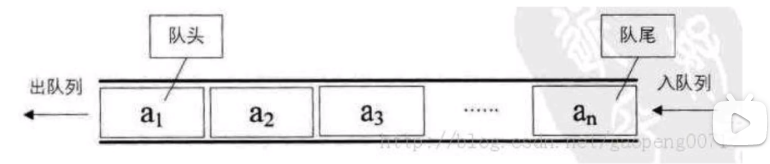
-
队列能否用列表简单实现?为什么?
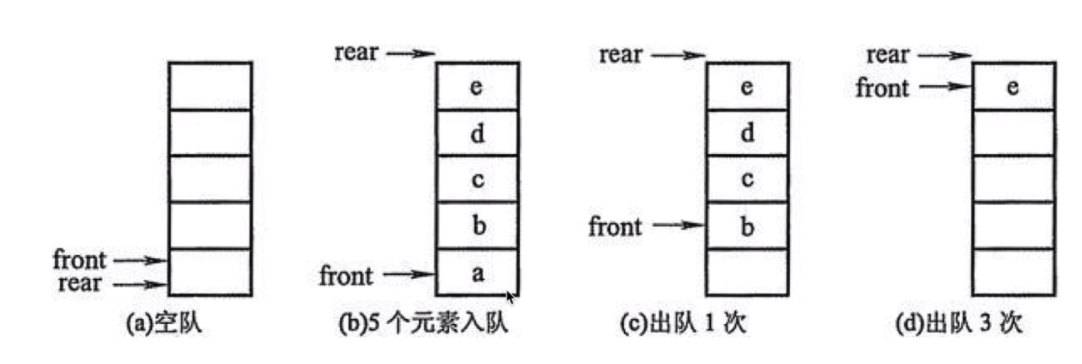
-
队列的实现方式--环形方式
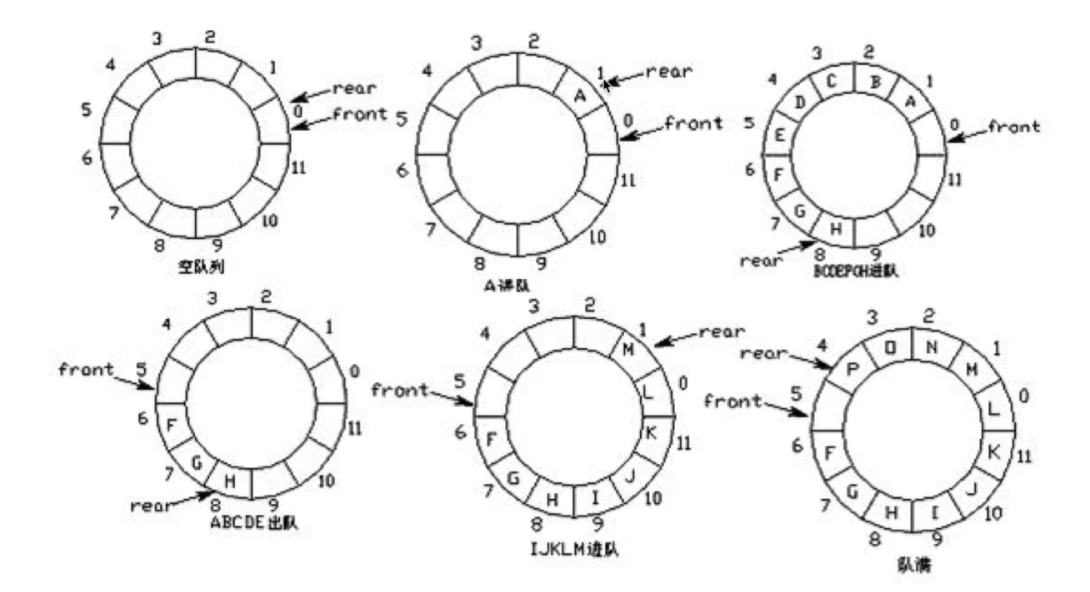
-
环形队列:当队尾指针front == Maxsize + 1时,再前进一个位置就自动到0.
-
队首指针前进1:front = (front + 1) % MaxSize
-
队尾指针前进1:rear = (rear + 1) % MaxSize
-
队空条件:rear = front
-
队满条件:(rear + 1)% MaxSize == front
- 队列实现

-
代码实现
 队列实现示例
队列实现示例class Queue: def __init__(self, size): self.__queue = [0 for _ in range(size)] self.size = size self.rear = 0 self.front = 0 def push(self, element): if not self.is_filled(): self.rear = (self.rear + 1) % self.size self.__queue[self.rear] = element else: raise IndexError('Queue is filled.') def pop(self): if not self.is_empty(): self.front = (self.front + 1) % self.size return self.__queue[self.front] raise IndexError('Queue is empty.') def is_empty(self): """ 判断队空 :return: """ return self.rear == self.front def is_filled(self): """ 判断队满 :return: """ return (self.rear + 1) % self.size == self.front if __name__ == '__main__': q = Queue(5) for i in range(4): q.push(i) while not q.is_empty(): print(q.pop())
-
-
常用场景:广度优先搜索
-
双端队列
-
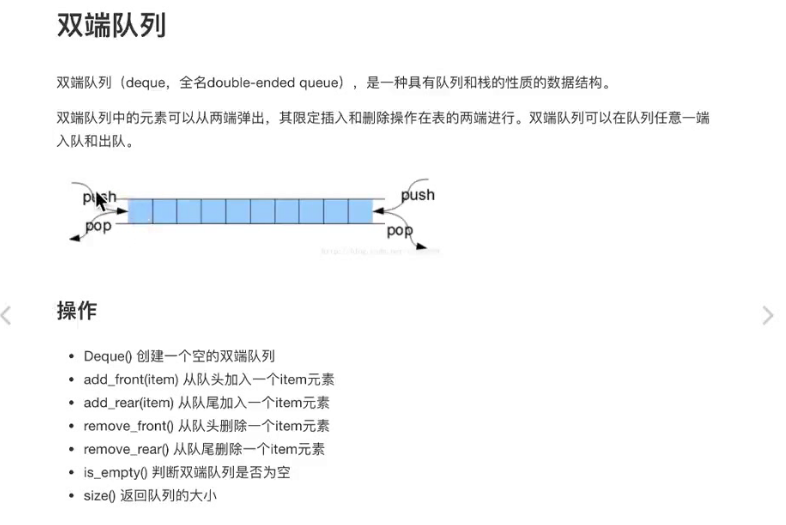

-
双向队列的两端都支持进队和出队操作
-
-
双向队列的基本操作:
-
队首进队
-
队首出队
-
-
队尾进队
-
队尾出队
-
-
-
Python队列内置模块
-
使用方法:from collections import deque
-
创建队列:queue = dequeue()
-
进队:append()
-
出队:popleft()
-
双向队列队首进队:appendleft()
-
栈和队列的应用--迷宫问题
-
-
栈--深度优先搜索

-
代码
 栈解决迷宫问题示例代码
栈解决迷宫问题示例代码maze=[ [1,1,1,1,1,1,1,1,1,1,1,1,1,1], [1,0,0,0,1,1,0,0,0,1,0,0,0,1], [1,0,1,0,0,0,0,1,0,1,0,1,0,1], [1,0,1,0,1,1,1,1,0,1,0,1,0,1], [1,0,1,0,0,0,0,0,0,1,1,1,0,1], [1,0,1,1,1,1,1,1,1,1,0,0,0,1], [1,0,1,0,0,0,0,0,0,0,0,1,0,1], [1,0,0,0,1,1,1,0,1,0,1,1,0,1], [1,0,1,0,1,0,1,0,1,0,1,0,0,1], [1,0,1,0,1,0,1,0,1,1,1,1,0,1], [1,0,1,0,0,0,1,0,0,1,0,0,0,1], [1,1,1,1,1,1,1,1,1,1,1,1,1,1] ] directions = [ lambda x, y: (x + 1, y), # 右 lambda x, y: (x - 1, y), # 左 lambda x, y: (x, y - 1), # 下 lambda x, y: (x, y + 1), # 上 ] def maze_path(x1, y1, x2, y2) -> (bool, list): stack = [] stack.append((x1, y1)) while len(stack) > 0: cur_node = stack[-1] # x, y四个方向 x-1, y;x+1, y;x, y-1;x, y+1; if cur_node[0] == x2 and cur_node[1] == y2: return True, stack for direction in directions: next_node = direction(cur_node[0], cur_node[1]) if maze[next_node[0]][next_node[1]] == 0: stack.append(next_node) maze[next_node[0]][next_node[1]] = 2 break else: maze[next_node[0]][next_node[1]] = 2 stack.pop() else: return False, [] if __name__ == '__main__': exist, path = maze_path(1,1, 10, 12) if exist: print('存在路径') for x, y in path: print(x, y) else: print('不存在路径')
-
-
队列--广度优先搜索

-
代码
 队列解决迷宫问题示例代码
队列解决迷宫问题示例代码from collections import deque maze=[ [1,1,1,1,1,1,1,1,1,1,1,1,1,1], [1,0,0,0,1,1,0,0,0,1,0,0,0,1], [1,0,1,0,0,0,0,1,0,1,0,1,0,1], [1,0,1,0,1,1,1,1,0,1,0,1,0,1], [1,0,1,0,0,0,0,0,0,1,1,1,0,1], [1,0,1,1,1,1,1,1,1,1,0,0,0,1], [1,0,1,0,0,0,0,0,0,0,0,1,0,1], [1,0,0,0,1,1,1,0,1,0,1,1,0,1], [1,0,1,0,1,0,1,0,1,0,1,0,0,1], [1,0,1,0,1,0,1,0,1,1,1,1,0,1], [1,0,1,0,0,0,1,0,0,1,0,0,0,1], [1,1,1,1,1,1,1,1,1,1,1,1,1,1] ] directions = [ lambda x, y: (x + 1, y), # 右 lambda x, y: (x - 1, y), # 左 lambda x, y: (x, y - 1), # 下 lambda x, y: (x, y + 1), # 上 ] def get_path(path) -> list: """ 遍历最优路径 :param path: :return: """ cur_node = path[-1] realpath = [] while cur_node[2] != -1: realpath.append(cur_node[0:2]) cur_node = path[cur_node[2]] realpath.append(cur_node[0:2]) realpath.reverse() return realpath def maze_path(x1, y1, x2, y2) -> (bool, list): """ 队列实现迷宫问题 :param x1: :param y1: :param x2: :param y2: :return: """ queue = deque() queue.append((x1, y1, -1)) path = [] while len(queue) > 0: cur_node = queue.pop() path.append(cur_node) if cur_node[0] == x2 and cur_node[1] == y2: best_path = get_path(path) return True, best_path for direction in directions: next_node = direction(cur_node[0], cur_node[1]) if maze[next_node[0]][next_node[1]] == 0: queue.append((next_node[0], next_node[1], len(path) - 1)) maze[next_node[0]][next_node[1]] = 2 else: print("不存在路径") return False, [] if __name__ == '__main__': exist, path = maze_path(1,1, 10, 12) if exist: print('存在路径') for node in path: print(node) else: print('不存在路径')
-
七、树

7.1 基础概念
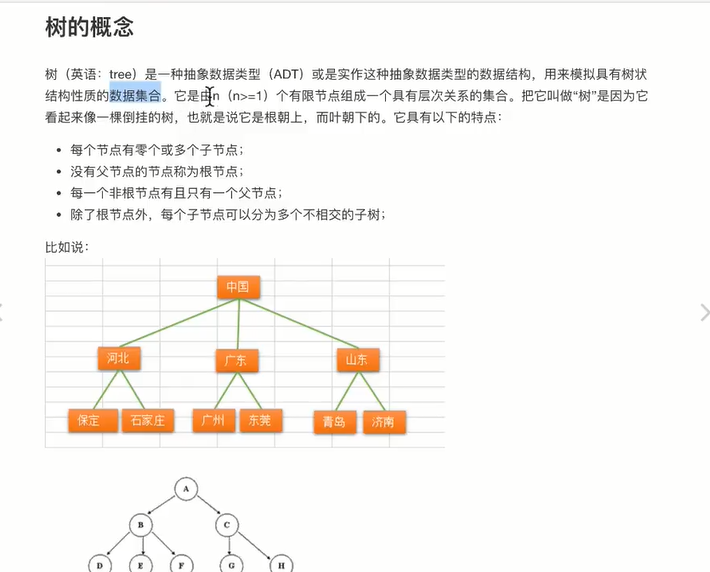
-
树是一种数据结构,比如:目录结构
-
树是一种可以递归定义的数据结构
-
树是由n个节点组成的集合
-
如果n=0,那这是一棵空树
-
如果n>0,那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个结合本身又是一棵树。
-
-
基本术语

- 树的种类

- 树的应用场景
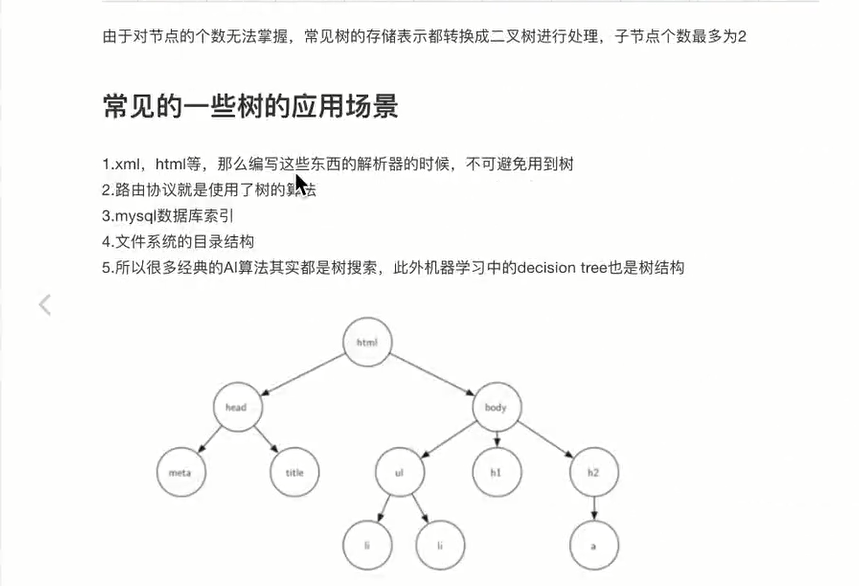
-
示例:文件系统
 树实现文件系统
树实现文件系统class Node(object): """ 链式存储 """ def __init__(self, name, type='folder'): self.name = name self.type = type self.children = [] self.parent = None def __repr__(self): return self.name class FileSystemTree: """ 文件系统:采用树结构 """ def __init__(self): self.root = Node('/') self.now = self.root def mkdir(self, name): if name[-1] != '/': name += "/" node = Node(name=name) self.now.children.append(node) node.parent = self.now def ls(self): return self.now.children def cd(self, name): if name[-1] != '/': name += '/' if name == '../': self.now = self.now.parent return for child in self.now.children: if child.name == name: self.now = child return raise ValueError('invalid dir') if __name__ == '__main__': tree = FileSystemTree() tree.mkdir('val/') tree.mkdir('bin/') tree.mkdir('usr/') tree.cd('bin/') tree.mkdir('python/') tree.cd('../') print(tree.ls()) # [val/, bin/, usr/]
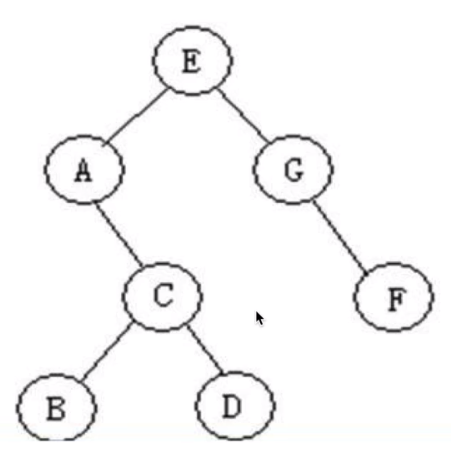
7.2 二叉树
-
二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接。
-
节点定义:
class Node: def __init__(self, data): self.data = data self.lchild = Node self.rchild = Node - 二叉树的性质
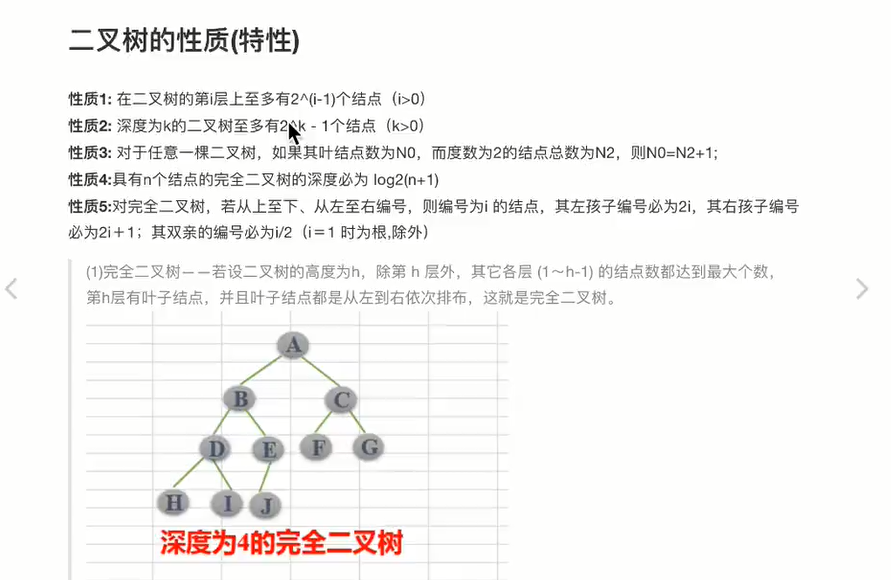
-
二叉树的遍历
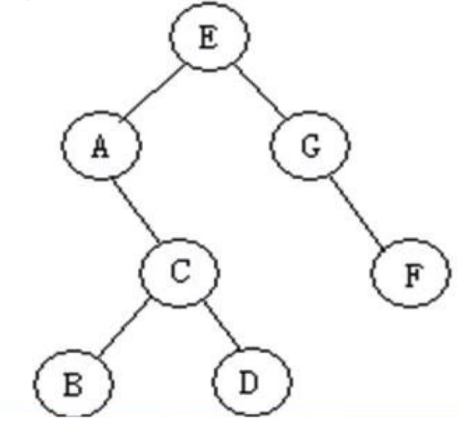
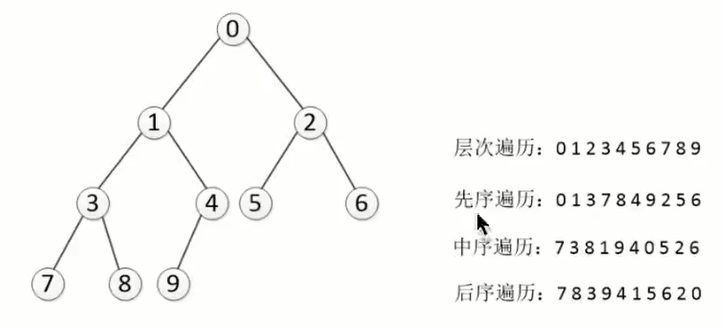
-
前序遍历:EACBDGF
-
中序遍历:ABCDEGF
-
后序遍历:BDCAFGE
-
层次遍历:EAGCFBD
-
代码
def bitree_test(): a = Node('A') b = Node('B') c = Node('C') d = Node('D') e = Node('E') f = Node('F') g = Node('G') e.lchild = a e.rchild = g a.rchild = c c.lchild = b c.rchild = d g.rchild = f level_travel(e) pre_order(e) print() in_order(e) print() post_order(e) print() """ 输出: E A G C F B D E A C B D G F A B C D E G F B D C A F G E """
-
-
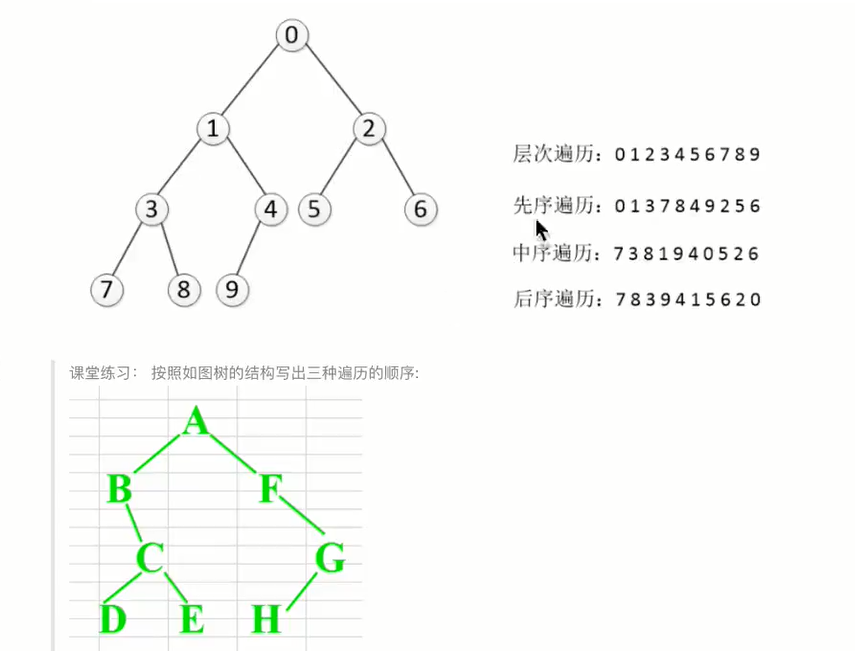
根据遍历序列确定一棵树
7.3 二叉搜索树

-
插入操作
def insert_no_rec(self, val): p = self.root if not p: self.root = Node(val) return while True: if val < p.data: if p.lchild: p = p.lchild else: p.lchild = Node(val) p.lchild.parent = p return elif val > p.data: if p.rchild: p = p.rchild else: p.rchild = Node(val) p.rchild.parent = p return else: return -
查询操作
def search(self, node: Node, val: int): if not node: return None if val < node.lchild: return self.search(node.lchild, val) elif val > node.rchild: return self.search(node.rchild, val) else: return node def search_no_rec(self, val) -> Node: p = self.root while p: if p.data < val: p = p.rchild elif p.data > val: p = p.lchild else: return p return None -
删除操作
-
如果要删除的佳钓尼是叶子节点,直接删除
-
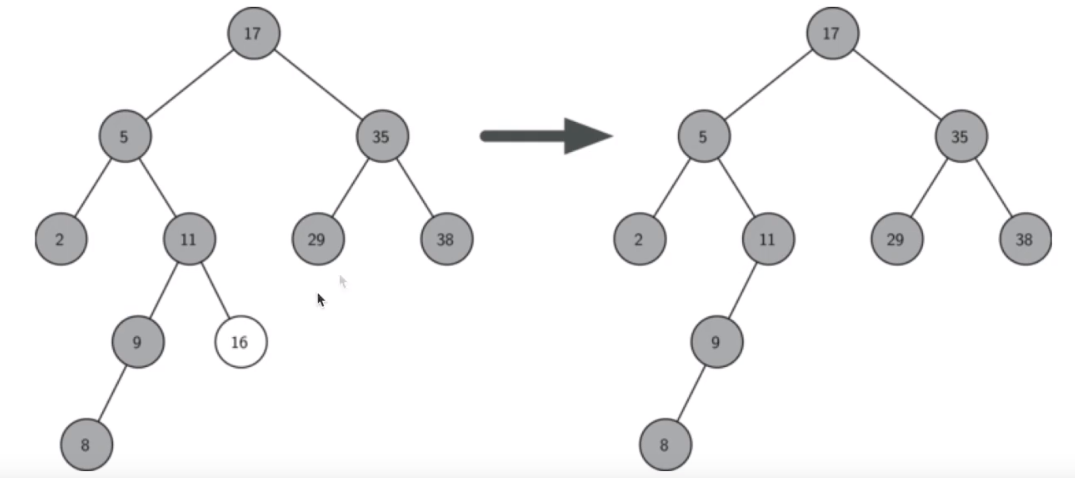
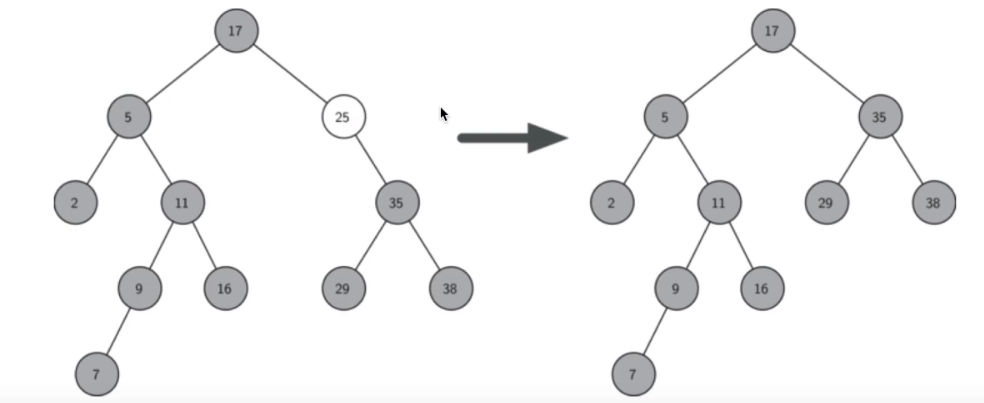
如果要删除的节点只有一个孩子:将此节点的父亲与孩子连接,然后删除该节点
-
如果要删除的节点有两个孩子:将其右子树的最小节点(该节点最优有一个右孩子)删除,并替换当前节点。
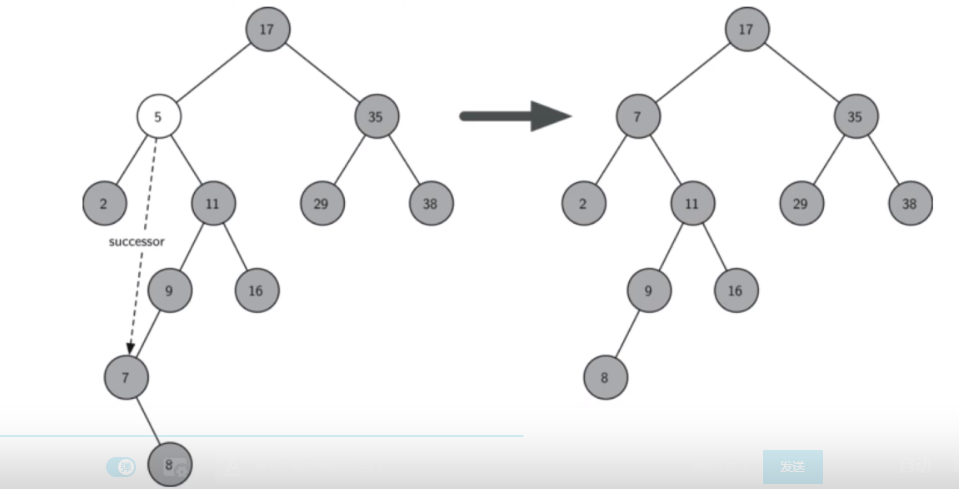
-
代码实现
class BST: ... def _remove_node_1(self, node: Node): if not node.parent: self.root = None if node == node.parent.lchild: node.parent.lchild = None else: node.parent.rchild = None def _remove_node_21(self, node: Node): if not node.parent: self.root = node.lchild node.lchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.lchild node.lchild.parent = node.parent else: node.parent.rchild = node.lchild node.lchild.parent = node.parent def _remove_node_22(self, node: Node): if not node.parent: self.root = node.rchild node.rchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.rchild node.rchild.parent = node.parent else: node.parent.rchild = node.rchild node.rchild.parent = node.parent def delete(self, val): if self.root: node = self.search_no_rec(val) if not node: return False if not node.lchild and not node.rchild: self._remove_node_1(node) elif not node.rchild: # 只有一个左孩子 self._remove_node_21(node) # 只有一个左孩子 elif not node.lchild: self._remove_node_22(node) # 只有一个右孩子 else: # 两个孩子都有 min_node = node.rchild while min_node.lchild: min_node = min_node.lchild node.elem = min_node.elem # 删除min_node if min_node.rchild: self._remove_node_22(min_node) else: self._remove_node_1(min_node) -
二叉搜索树的效率
-
平均情况下,二叉搜索树进行搜索的时间复杂度为O(logn)。
-
最坏情况下,二叉搜索树可能非常偏斜。
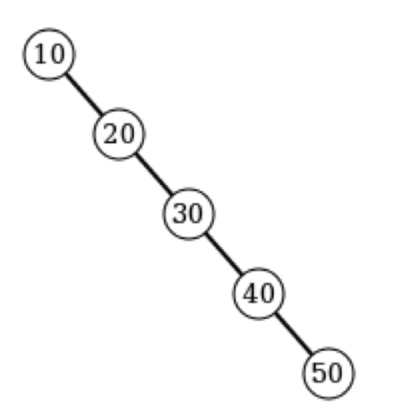
-
解决方案:
-
随机化插入
-
AVL树
-
-
-
7.4 AVL树
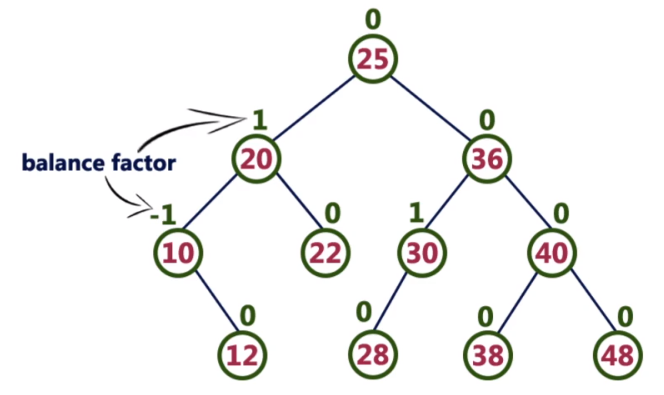
-
AVL树:AVL树是一棵自平衡的二叉搜索树。
-
AVL树具有以下性质:
-
根的左右子树的高度之差绝对值不能超过1
-
根的左右子树都是平衡二叉树
-
-
插入

-
不平衡是由于对K的右孩子的右子树插入导致的:左旋
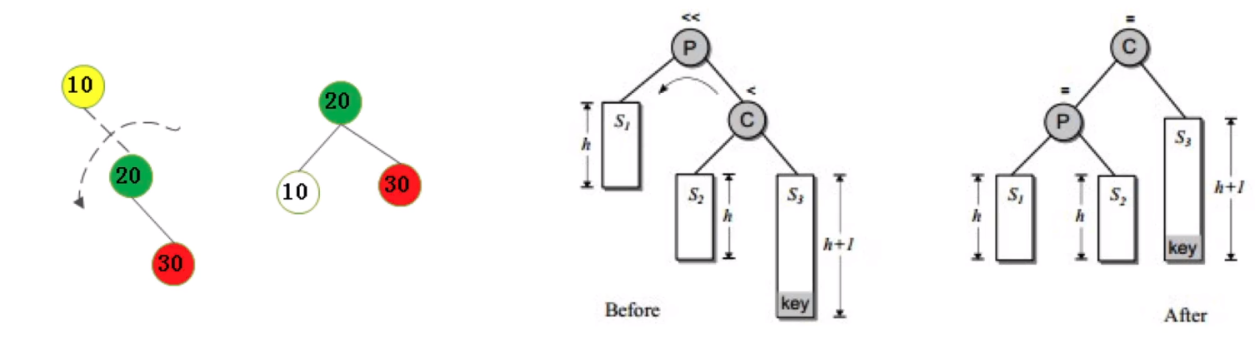
-
不平衡是由于对K的左孩子的左子树插入导致的:右旋
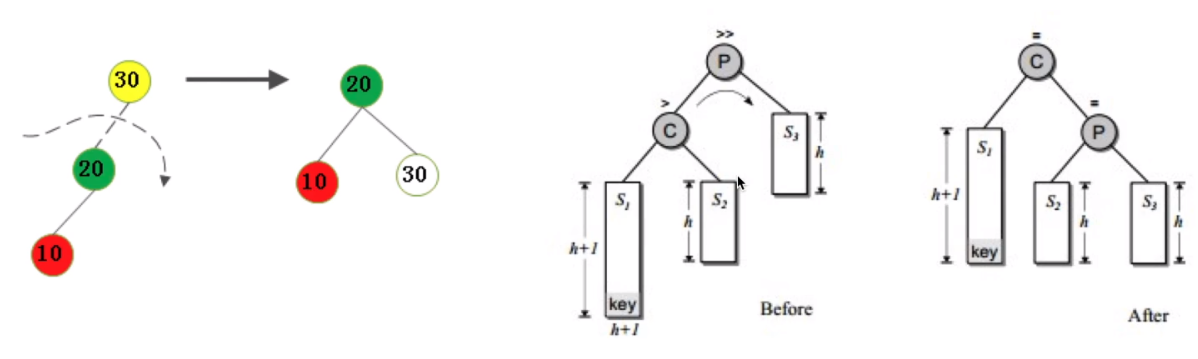
-
不平衡由于对K的右孩子的左子树插入导致的:右旋-左旋
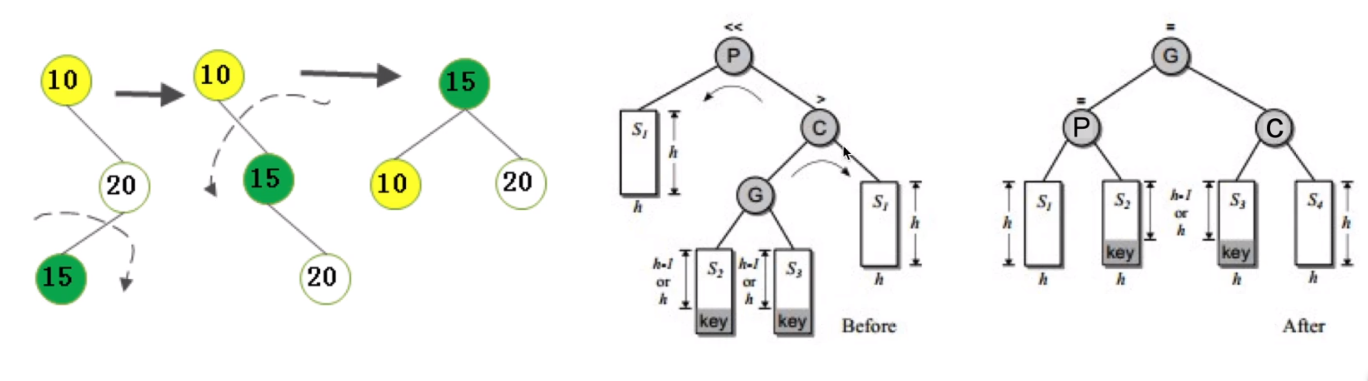
-
不平衡是由于对K的左孩子的右子树插入导致的:左旋-右旋
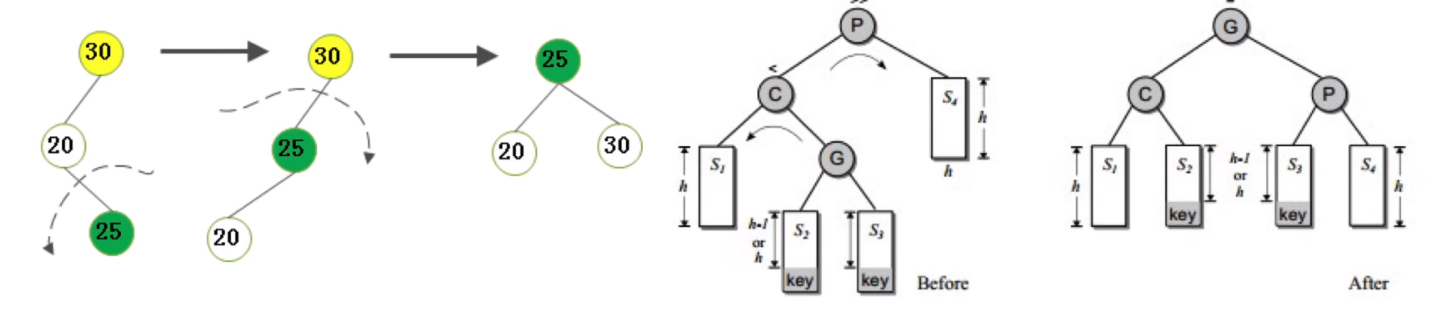
-
-
代码实现
binary_search_tree.py
 二分搜索树
二分搜索树class Node: def __init__(self, data): self.data = data self.lchild = None self.rchild = None self.parent = None class BST: def __init__(self, node_list: list = None): self.root = None if node_list: for node in node_list: self.insert_no_rec(node) def insert(self, node: Node, val: int): """ 二叉搜索树: 插入 :param node: :param val: :return: """ if not node: node = Node(val) elif val < node.data: node.lchild = self.insert(node.lchild, val) node.lchild.parent = node elif val > node.data: node.rchild = self.insert(node.rchild, val) node.rchild.parent = node return node def insert_no_rec(self, val): p = self.root if not p: self.root = Node(val) return while True: if val < p.data: if p.lchild: p = p.lchild else: p.lchild = Node(val) p.lchild.parent = p return elif val > p.data: if p.rchild: p = p.rchild else: p.rchild = Node(val) p.rchild.parent = p return else: return def search(self, node: Node, val: int): if not node: return None if val < node.lchild: return self.search(node.lchild, val) elif val > node.rchild: return self.search(node.rchild, val) else: return node def search_no_rec(self, val) -> Node: p = self.root while p: if p.data < val: p = p.rchild elif p.data > val: p = p.lchild else: return p return None def preorder(self, node): """先序遍历""" if not node: return print(node.data, end=' ') self.preorder(node.lchild) self.preorder(node.rchild) def inorder(self, node): """中序遍历""" if not node: return self.inorder(node.lchild) print(node.data, end=' ') self.inorder(node.rchild) def postorder(self, node): """后序遍历""" if not node: return self.postorder(node.lchild) self.postorder(node.rchild) print(node.data, end=' ') def _remove_node_1(self, node: Node): if not node.parent: self.root = None if node == node.parent.lchild: node.parent.lchild = None else: node.parent.rchild = None def _remove_node_21(self, node: Node): if not node.parent: self.root = node.lchild node.lchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.lchild node.lchild.parent = node.parent else: node.parent.rchild = node.lchild node.lchild.parent = node.parent def _remove_node_22(self, node: Node): if not node.parent: self.root = node.rchild node.rchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.rchild node.rchild.parent = node.parent else: node.parent.rchild = node.rchild node.rchild.parent = node.parent def delete(self, val): if self.root: node = self.search_no_rec(val) if not node: return False if not node.lchild and not node.rchild: self._remove_node_1(node) elif not node.rchild: # 只有一个左孩子 self._remove_node_21(node) # 只有一个左孩子 elif not node.lchild: self._remove_node_22(node) # 只有一个右孩子 else: # 两个孩子都有 min_node = node.rchild while min_node.lchild: min_node = min_node.lchild node.data = min_node.data # 删除min_node if min_node.rchild: self._remove_node_22(min_node) else: self._remove_node_1(min_node)
avl_tree.py
 平衡二叉树
平衡二叉树from binary_search_tree import Node, BST class AVLNode(Node): def __init__(self, data): Node.__init__(self, data) self.bf = 0 class AVLTree(BST): def __init__(self, data_list: list = None): BST.__init__(self, data_list) def rotate_left(self, p: AVLNode, c: AVLNode): s2 = c.lchild p.rchild = s2 if s2: s2.parent = p c.lchild = p p.parent = c p.bf = 0 c.bf = 0 return c def rotate_right(self, p: AVLNode, c: AVLNode): s2 = c.rchild p.lchild = s2 if s2: s2.parent = p c.rchild = p p.parent = c p.bf = 0 c.bf = 0 return c def rotate_right_left(self, p: AVLNode, c: AVLNode): g = c.lchild # right rotate s3 = g.rchild c.lchild = s3 if s3: s3.parent = c g.rchild = c c.parent = g # left rotate s2 = g.lchild p.rchild = s2 if s2: s2.parent = p g.lchild = p p.parent = g # 更新bf if g.bf > 0: p.bf = -1 c.bf = 0 else: p.bf = 0 c.bf = 1 g.bf = 0 return g def rotate_left_right(self, p: AVLNode, c: AVLNode): g = c.rchild # right rotate s2 = g.lchild c.rchild = s2 if s2: s2.parent = c g.lchild = c c.parent = g # left rotate s3 = g.rchild p.lchild = s3 if s3: s3.parent = p g.rchild = p p.parent = g # 更新bf if g.bf > 0: p.bf = 0 c.bf = -1 else: p.bf = 1 c.bf = 0 g.bf = 0 return g def insert_no_rec(self, val): # 1. 插入节点 p = self.root if not p: self.root = AVLNode(val) return while True: if val < p.data: if p.lchild: p = p.lchild else: p.lchild = AVLNode(val) p.lchild.parent = p node = p.lchild break elif val > p.data: if p.rchild: p = p.rchild else: p.rchild = AVLNode(val) p.rchild.parent = p node = p.rchild break else: return # 2. 更新balance factor while node.parent: if node.parent.lchild == node: # 传递是从左子树来的,左子树更沉了 # 更新node.parent的bf -= 1 if node.parent.bf < 0: # 原来node.parent.bf == -1, 更新后变成-2 # 做旋转 # 看node哪边沉 g = node.parent.parent # 为了连接旋转之后的子树 x = node.parent # 选赚钱子树的根 if node.bf > 0: n = self.rotate_left_right(node.parent, node) else: n = self.rotate_right(node.parent, node) # 记得:把n和g连起来 elif node.parent.bf > 0: # 原来node.parent.bf = 1. 更新之后变成0 node.parent.bf = 0 break else: # 原来node.parent.bf = 0,更新之后变成-1 node.parent.bf = -1 node = node.parent continue else: # 传递是从右子树来的,右子树更沉了 # 更新node.parent.bf += 1 if node.parent.bf > 0: # 原来node.parent.bf == 1, 更新后变成2 # 做旋转 # 看node哪边沉 g = node.parent.parent # 为了连接旋转之后的子树 x = node.parent # 选赚钱子树的根 if node.bf < 0: # node.bf = 1 n = self.rotate_right_left(node.parent, node) else: # node.bf = -1 n = self.rotate_left(node.parent, node) # 记得连起来 elif node.parent.bf < 0: node.parent.bf = 0 break else: node.parent.bf = 1 node = node.parent continue # 连接旋转后的子树 n.parent = g if g: # G不是空 if x == g.lchild: g.lchild = n else: g.rchild = n break else: self.root = n break if __name__ == '__main__': tree = AVLTree([9,8,7,6,5,4,3,2,1]) tree.preorder(tree.root) print() tree.inorder(tree.root)
7.5 二叉搜索树的扩展应用--B树
-
B树(B-Tree):B树是一棵自平衡的多路搜索树。常用于数据库的索引。
-

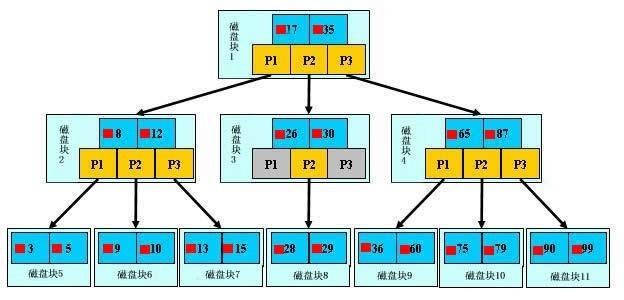
-
树的共性
结构直观
通过树问题来考察 递归算法 掌握的熟练程度
-
⾯试中常考的树的形状有
普通⼆叉树
平衡⼆叉树
完全⼆叉树
⼆叉搜索树
四叉树
多叉树
特殊的树:红⿊树、⾃平衡⼆叉搜索树
-
遍历
前序遍历(Preorder Traversal)
中序遍历(Inorder Traversal)
后序遍历(Postorder Traversal)
高级数据结构
一. 优先队列 / Priority Queue
-
与普通队列的区别
优先级别克自定义
-
最常用的场景
从杂乱无章的数据中按照一定的顺序(或者优先级)筛选数据
-
本质
二叉堆的结构,堆在英文里叫Binary Heap
利用一个数组结构来实现完全二叉树

-
特性
数组里的第一个元素拥有最高的优先级
对于一个下标i,那么对于元素aray[i]而言
-
父节点 对应的元素下标是(i-1)/2
-
左侧子节点 对应的元素下标是 2*i + 1
-
右侧子节点 对应的元素下标是 2*i + 2
数组中每个元素的优先级都必须高于它两侧子节点
-
-
其基本操作有一下两个
向上筛选(sift up / bubble up)
向下筛选(sift down / bubble down)
-
优先队列的初始化时间复杂度是O(n)
二、 图/ Graph
-
最基本的知识点
阶、度
树、森铃、环
有向图、无向图、完全有向图、完全无向图
连通图、连通分量
图的存储和表达方式:邻接矩阵、链表链表
-
图的算法
图的遍历:深度优先、广度优先
环的检测:有向图、无向图
拓扑排序
最短路径算法:Dijkstra 、Bellman-Ford 、Floyd Warshal
连通性相关算法:Kosaraju 、Tarjan̵、求解孤岛的数量、判断是否为树
图的着色、旅行商问题等
-
必须掌握的知识点
图的存储和表达方式:邻接矩阵、链表链表
图的遍历:深度优先、广度优先
二部图的检测、树的检测、环的检测、有向图、无向图
拓扑排序
联合查找算法
最短路径:Dijkstra 、Bellman-Ford
三、前缀树 / Trie
-
也称字典树
这种数据结构被广泛地运用在字典查找当中
-
什么是字典查找?
例如:给定一系列构成字典的字符串、要求在字典当中找出所有以“ABC”开头的字符串
-
方法一:暴力搜索法
时间复杂度:O(M*N)
-
方法二:前缀树
时间复杂度:O(M)
-
-
经典应用
搜索框输入搜索文字,会罗列以搜索词开头的相关搜索
汉语拼音输入法
-
重要性质
每个节点至少包含两个基本属性
-
children:数组或者集合,罗列出每个分支当中包含的所有字符
-
isEnd:布尔值,表示该节点是否为某字符串的结尾
根节点是空的
除了根节点,其他节点都可能是单词的结尾,叶子节点一定都是单词的结尾
-
-
最基本的操作
创建
方法
-
遍历一遍输入的字符串、对每个字符串的字符进行遍历
-
从前缀树的根节点开始,将每个字符加入到节点的children字符集当中
-
如果字符集已经包含这个字符,跳过
-
如果当前字符是字符串的最后一个,把当前节点的isEnd标记为真
搜索
方法
-
从前缀树的根节点触发,逐个匹配输入的前缀字符
-
如果遇到了,继续往下一层搜索
-
如果没遇到,立即返回
-
四、 线段树/Segment Tree
-
什么是线段树?
一种按照二叉树的形式存储数据的结构,每个节点保存的都是数组里某一段的总和
例如数组是[1,3,5,7,9]
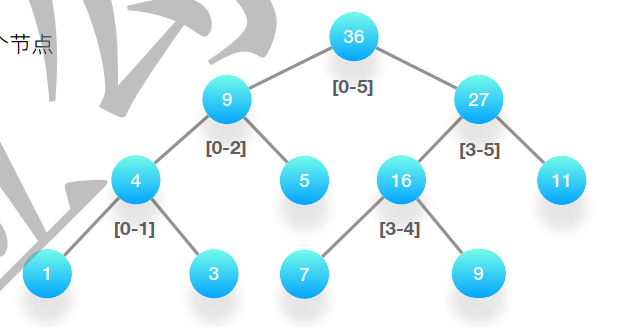
五、树状数组 / Fenwick Tree / Binary Indexed Tre
-
重要的基本特征
利用数组来表述多叉树的结构,和优先队列有些相似
优先队列使用数组来表示完全二叉树,而树状数组是多叉树
树状数组的第一个元素是空节点
如果节点tree[y]是tree[x]的父节点,那么需要满足y = x - (x & (-x))
-
例题
假设我们有一个数组,里面有n个元素,现在我们要经常的对这个数组做两件事
-
更新数组的数值
-
求数组前k个元素的总和(或者平均值)
方法一:线段树
时间复杂度: O(logn)
方法二:树状数组
时间复杂度: O(logn)
-








