Numpy系列（一）- array

初始Numpy

一、什么是Numpy?

简单来说，Numpy 是 Python 的一个科学计算包，包含了多维数组以及多维数组的操作。

Numpy 的核心是 ndarray 对象，这个对象封装了同质数据类型的n维数组。起名 ndarray 的原因就是因为是 n-dimension-array 的简写。

二、ndarray 与 python 原生 array 有什么区别

NumPy 数组在创建时有固定的大小，不同于Python列表（可以动态增长）。更改ndarray的大小将创建一个新的数组并删除原始数据。

NumPy 数组中的元素都需要具有相同的数据类型，因此在存储器中将具有相同的大小。数组的元素如果也是数组（可以是 Python 的原生 array，也可以是 ndarray）的情况下，则构成了多维数组。

NumPy 数组便于对大量数据进行高级数学和其他类型的操作。通常，这样的操作比使用Python的内置序列可能更有效和更少的代码执行。越来越多的科学和数学的基于Python的包使用NumPy数组，所以需要学会 Numpy 的使用。

三、Numpy 的矢量化（向量化）功能

如果想要将一个2-D数组 a 的每个元素与长度相同的另外一个数组 b 中相应位置的元素相乘，使用 Python 原生的数组实现如下：

for (i = 0; i < rows; i++): {
  for (j = 0; j < columns; j++): {
    c[i][j] = a[i][j]*b[i][j];
  }}

使用 Numpy 实现的话，则可以直接使用矢量化功能：

c = a * b

矢量化代码有很多优点，其中包括：

矢量化代码更简洁易读
更少的代码行通常意味着更少的错误
该代码更接近地类似于标准数学符号（使得更容易，通常，以正确地编码数学构造）
矢量化导致更多的“Pythonic”代码。如果没有向量化，我们的代码将会效率很低，难以读取for循环。

N维数组 ndarray

Numpy 中最重要的一个对象就是 ndarray。
ndarray 结构图

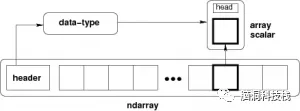
ndarray中的每个元素在内存中使用相同大小的块。 ndarray中的每个元素是数据类型对象的对象(称为 dtype)。
从ndarray对象提取的任何元素(通过切片)由一个数组标量类型的 Python 对象表示。下图显示了ndarray，数据类型对象(dtype)和数组标量类型之间的关系。

一、构建ndarray

import numpy as np
#一维数组
a = np.array([0,1,2,3])
a
Out[39]: array([0, 1, 2, 3])
#二维数组
b = np.array([[0,1,2],[4,5,6]])
b
Out[40]: 
array([[0, 1, 2],
       [4, 5, 6]])
#创建一个0-9的数组
a = np.arange(10)
a
Out[41]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
#创建一个1-6，步长为2的数组
b = np.arange(1,6,2)
b
Out[42]: array([1, 3, 5])

二、常用的数组

# 全一矩阵
np.ones((3,3))
Out[43]: 
array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])
# 零矩阵
np.zeros((2,2))
Out[44]: 
array([[0., 0.],
       [0., 0.]])
# 单位矩阵
np.eye(3)
Out[45]: 
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
# 对角矩阵
np.diag(np.array([1,2,3,4]))
Out[46]: 
array([[1, 0, 0, 0],
       [0, 2, 0, 0],
       [0, 0, 3, 0],
       [0, 0, 0, 4]])

三、生成等差数列

linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None):

endpoint: 结束点如果现在为True，那么输入的第二个参数将会成为数列的最后一个元素，反之则不一定。
restep: 而retstep会改变计算的输出，输出一个元组，而元组的两个元素分别是需要生成的数列和数列的步进差值。

# 默认生成50个元素的等差序列，需设定起始值和终止值
np.linspace(1,10)
Out[47]: 
array([ 1.        ,  1.18367347,  1.36734694,  1.55102041,  1.73469388,
        1.91836735,  2.10204082,  2.28571429,  2.46938776,  2.65306122,
        2.83673469,  3.02040816,  3.20408163,  3.3877551 ,  3.57142857,
        3.75510204,  3.93877551,  4.12244898,  4.30612245,  4.48979592,
        4.67346939,  4.85714286,  5.04081633,  5.2244898 ,  5.40816327,
        5.59183673,  5.7755102 ,  5.95918367,  6.14285714,  6.32653061,
        6.51020408,  6.69387755,  6.87755102,  7.06122449,  7.24489796,
        7.42857143,  7.6122449 ,  7.79591837,  7.97959184,  8.16326531,
        8.34693878,  8.53061224,  8.71428571,  8.89795918,  9.08163265,
        9.26530612,  9.44897959,  9.63265306,  9.81632653, 10.        ])
# 生成指定个数的等差序列
np.linspace(1,10,10)
Out[48]: array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

四、生成等比数列

logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)

base:等比基数默认为10

# 创建10个1-1的等比数列， 因为默认基数是10  
np.logspace(0, 0, 10)
Out[55]: array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
# 创建10个1-2的10次方之间的等比数列， 改变等比基数
np.logspace(0, 9, 10, base=2)
Out[59]: array([  1.,   2.,   4.,   8.,  16.,  32.,  64., 128., 256., 512.])
# 创建10个1-2的10次方之间的等比数列， 改变等比基数
np.logspace(0, 9, 10, base=2, dtype=int)
Out[60]: array([  1,   2,   4,   8,  16,  32,  64, 128, 256, 512])

五、生成meshgrid网格矩阵

meshgrid函数通常在数据的矢量化上使用，但是使用的方法我暂时还不是很明确。而meshgrid的作用适用于生成网格型数据，可以接受两个一维数组生成两个二维矩阵，对应两个数组中所有的(x,y)对。接下来通过简单的shell交互来演示一下这个功能的使用，并做一下小结。

meshgrid(*xi, **kwargs)

功能：从一个坐标向量中返回一个坐标矩阵

参数：

x1,x2...,xn：数组,一维的数组代表网格的坐标。

indexing：{'xy','ij'}，笛卡尔坐标'xy'或矩阵'ij'下标作为输出，默认的是笛卡尔坐标。

sparse：bool类型，如果为True，返回一个稀疏矩阵保存在内存中，默认是False。

copy：bool类型，如果是False，返回一个原始数组的视图保存在内存中，默认是True。如果，sparse和copy都为False，将有可能返回一个不连续的数组。而且，如果广播数组的元素超过一个，可以使用一个独立的内存。如果想要对这个数组进行写操作，请先拷贝这个数组。

返回值：x1,x2,....,xn：ndarray(numpy数组)

参数

例子

x = np.linspace(1, 3, 3)
x
Out[69]: array([1., 2., 3.])
y = np.linspace(4, 7, 4)
y
Out[71]: array([4., 5., 6., 7.])
xv, yv = np.meshgrid(x, y)
xv
Out[73]: 
array([[1., 2., 3.],
       [1., 2., 3.],
       [1., 2., 3.],
       [1., 2., 3.]])
yv
Out[74]: 
array([[4., 4., 4.],
       [5., 5., 5.],
       [6., 6., 6.],
       [7., 7., 7.]])

通过上面的例子，其实可以发现meshgrid函数将两个输入的数组x和y进行扩展，前一个的扩展与后一个有关，后一个的扩展与前一个有关，前一个是竖向扩展，后一个是横向扩展。因为，y的大小为4，所以x竖向扩展为原来的四倍，而x的大小为3，所以y横向扩展为原来的3倍。通过meshgrid函数之后，输入由原来的数组变成了一个矩阵。通过使用meshgrid函数，可以产生一个表格矩阵，下面用一个例子来展示产生一个2*2网格的坐标，每个网格的大小为1。

# 生成一个2*2的网格的坐标
#从0开始到1结束，返回一个numpy数组,nx代表数组中元素的个数
x = np.linspace(0,2,3)
x
Out[77]: array([0., 1., 2.])
y = np.linspace(0,2,3)
y
Out[79]: array([0., 1., 2.])
xv,yv = np.meshgrid(x,y)
print(xv.ravel())
print(yv.ravel())
[0. 1. 2. 0. 1. 2. 0. 1. 2.]
[0. 0. 0. 1. 1. 1. 2. 2. 2.]

　ravel函数是将矩阵变为一个一维的数组，其中xv.ravel()就表示x轴的坐标，yv.ravel()就表示了y轴的坐标，我们将x轴的坐标和y轴的坐标进行一一对应，就产生了一个2*2大小为1的网格中的9个点的坐标。

如果，将sparse参数设置为True，就不会向上面一样进行扩展了，也就是说它产生的网格坐标不是所有的网格坐标，而是网格对角线上的坐标点。

nx,ny = (3,3)
#从0开始到1结束，返回一个numpy数组,nx代表数组中元素的个数
x = np.linspace(0,2,nx)
# [0. 1. 2.]
y = np.linspace(0,2,ny)
# [0. 1. 2.]
xv,yv = np.meshgrid(x,y,sparse=True)
print(xv)
[[0. 1. 2.]]

六、创建行列向量

np.r_[0:50:5]
Out[84]: array([ 0,  5, 10, 15, 20, 25, 30, 35, 40, 45])
np.c_[0:50:5]
Out[85]: 
array([[ 0],
       [ 5],
       [10],
       [15],
       [20],
       [25],
       [30],
       [35],
       [40],
       [45]])

　七、生成随机数组

np.random.seed(1234) #设置随机种子为1234
np.random.rand(2,3) #2行3列均匀分布
np.random.randn(2,3) #Gaussian
np.random.randn(3,3) #三行三列正态分布随机数据
np.random.randint(1,3,5) #min max size 产生min-max中size个整数
np.random.randint(1,100,[5,5]) #(1,100）以内的5行5列随机整数
np.random.random(10) #(0,1）以内10个随机浮点数
np.random.sample(10) #产生0，1内10个随机数
np.random.choice(10) #[0,10)内随机选择一个数

np.random.rand(2,3) #2行3列均匀分布
Out[86]: 
array([[0.10437154, 0.25867737, 0.60777109],
       [0.21729078, 0.38925987, 0.69986437]])
np.random.randn(2,3) #Gaussian
Out[87]: 
array([[ 0.18813823,  0.21829928,  1.30977936],
       [-0.80801174, -0.2710817 ,  0.30614839]])
np.random.randn(3,3) #三行三列正态分布随机数据
Out[88]: 
array([[ 0.31102522,  0.24991538, -0.74242789],
       [-0.92471694,  0.09958997, -0.03147058],
       [-0.31209779,  0.94883746, -0.71359588]])
np.random.randint(1,3,5) #min max size 产生min-max中size个整数 
Out[89]: array([1, 2, 2, 1, 1])
np.random.randint(1,100,[5,5]) #(1,100）以内的5行5列随机整数
Out[90]: 
array([[71, 80, 19, 13, 56],
       [40, 51, 42, 10, 65],
       [14, 87, 91, 36, 29],
       [27, 43, 24, 19, 31],
       [89, 79, 97, 21, 24]])
np.random.random(10) #(0,1）以内10个随机浮点数
Out[91]: 
array([0.31589784, 0.04031992, 0.57425601, 0.57655811, 0.36513947,
       0.19312436, 0.22195245, 0.94515895, 0.85251243, 0.06609203])
np.random.sample(10) #产生0，1内10个随机数
Out[92]: 
array([0.47695889, 0.75269019, 0.31765674, 0.53586716, 0.94818987,
       0.50960077, 0.32388153, 0.43584506, 0.00900502, 0.03402676])
np.random.choice(10) #[0,10)内随机选择一个数
Out[93]: 2

八、ndaaray常用属性

`ndarray.flags`	有关数组的内存布局的信息。
`ndarray.shape`	数组维数组。
`ndarray.strides`	遍历数组时，在每个维度中步进的字节数组。
`ndarray.ndim`	数组维数，在Python世界中，维度的数量被称为rank。
`ndarray.data`	Python缓冲区对象指向数组的数据的开始。
`ndarray.size`	数组中的元素总个数。
`ndarray.itemsize`	一个数组元素的长度（以字节为单位）。
`ndarray.nbytes`	数组的元素消耗的总字节数。
`ndarray.base`	如果内存是来自某个其他对象的基本对象。
`ndarray.dtype`	数组元素的数据类型。
`ndarray.T`	数组的转置。

a = np.array([(1,2,3),(4,5,6)])
a
Out[95]: 
array([[1, 2, 3],
       [4, 5, 6]])
a.flags
Out[96]: 
  C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False
a.shape
Out[97]: (2, 3)
a.ndim
Out[98]: 2
a.strides
Out[99]: (12, 4)
a.data
Out[100]: <memory at 0x0000004E715C8B40>
a.size
Out[101]: 6
a.itemsize
Out[102]: 4
a.nbytes
Out[103]: 24
a.base
a.dtype
Out[105]: dtype('int32')
a.T
Out[106]: 
array([[1, 4],
       [2, 5],
       [3, 6]])

posted @ 2019-03-20 19:03 DreamBoy_张亚飞阅读(934) 评论(0) 编辑收藏举报

刷新页面返回顶部

超级英雄拯救世界之前成长的日子