注意:
- 关系代数有关符号,大家可能又不熟悉了,点击跳转:(数据库系统概论|王珊)第二章关系数据库-第四节:关系代数
@
目录
在(数据库系统概论|王珊)第九章关系查询处理和关系优化-第一节:查询处理中讲到过:SQL语句经过查询分析,查询检查后变换为查询树,它是关系代数表达式的内部表示。本节介绍查询优化之代数优化,它是基于关系代数等价变换规则的优化方法
- 两个关系表达式\(R_{1}\)和\(R_{2}\)是等价的,可以记为\(R_{1} \equiv R_{2}\)
一:关系代数表达式等价变换规则
- 为了能方便阅读,就没用截图。手都麻了🤮(动动手点个赞吧🥳)
![在这里插入图片描述]()
(1)连接、笛卡尔积、并、交的交换律
笛卡尔积
\[R×S \equiv S×R
\]
并
\[R \cup S \equiv S \cup R
\]
交
\[R \cap S \equiv S \cap R
\]
连接
\[R \underset{F}{\bowtie} S \equiv S \underset{F}{\bowtie} R 、
R\bowtie S \equiv S\bowtie R\]
(2)连接、笛卡尔积、并、交的结合律
笛卡尔积
\[(R×S) ×T\equiv R×(S×T)
\]
并
\[(R \cup S)\cup T \equiv R \cup (S\cup T)
\]
交
\[(R \cap S)\cap T \equiv R \cap (S\cap T)
\]
连接
\[(R \underset{F}{\bowtie} S) \underset{F}{\bowtie} T \equiv R \underset{F}{\bowtie} (S \underset{F}{\bowtie} T)
\]
\[(R\bowtie S) \bowtie T \equiv R\bowtie (S \bowtie T)
\]
(3)投影的串接定律
关系的两次投影操作可以合并为一次完成(反过来就是分解)
\[\Pi_{A_{1},A_{2},...,A_{n}}(\Pi_{B_{1},B_{2},...,B_{m}}(E)) \equiv \Pi_{A_{1},A_{2},...,A_{n}}(E)
\]
- \(E\)是关系代数表达式
- \(A_{i}(i=1,2,..,n),B_{j}(j=1,2,..,m)\)是属性名。并且\(\{ {A_{1},A_{2},...,A_{n}} \}\)构成\(\{ {B_{1},B_{2},...,B_{m}} \}\)的子集
(4)选择的串接定律
选择的两次投影操作可以合并为一次完成(反过来就是分解)
\[\sigma_{F1}(\sigma_{F2}(E)) \equiv \sigma_{F1\land F2}(E)
\]
(5)选择与投影的交换律
\[\sigma_{F}(\Pi_{A_{1},A_{2},...,A_{n}}(E)) \equiv \Pi_{A_{1},A_{2},...,A_{n}}(\sigma_{F}(E))
\]
- 假设:选择条件\(F\)只涉及属性\({A_{1},A_{2},...,A_{n}}\)
\[\Pi_{A_{1},A_{2},...,A_{n}}(\sigma_{F}(E)) \equiv \Pi_{A_{1},A_{2},...,A_{n}}(\sigma_{F}( \Pi_{A_{1},A_{2},...,A_{n},B_{1},B_{2},...,B_{m}}(E)))
\]
- 假设:\(F\)中有不属于\({A_{1},A_{2},...,A_{n}}\)的属性\({B_{1},B_{2},...,B_{m}}\)
(6)选择与笛卡尔积的交换律
对于\(\sigma_{F}(E_{1}×E_{2})\),有如下等价
①
\[\sigma_{F}(E_{1}×E_{2}) \equiv \sigma_{F}(E_{1})×E_{2}
\]
- 假设:选择条件只与其中的一个关系有关,应该对那个关系先做选择,然后再做笛卡尔积。例如上面\(F\)中涉及的属性都是\(E_{1}\)中的属性
②
\[\sigma_{F}(E_{1}×E_{2}) \equiv \sigma_{F_{1}}(E_{1})×\sigma_{F_{2}}(E_{2})
\]
- 假设:选择条件与两个关系都有关,应该先分别做选择,然后再做笛卡尔积。例如上面\(F=F_{1} \land F_{2}\),并且\(F_{1}\)中只涉及\(E_{1}\)中的属性,\(F_{2}\)中只涉及\(E_{2}\)中的属性
③
\[\sigma_{F}(E_{1}×E_{2}) \equiv \sigma_{F_{2}}(\sigma_{F_{1}}(E_{1})×E_{2})
\]
- 假设:如果选择条件与某一部分关系有关,那么也应该先对那个关系做部分选择,然后做笛卡尔积,最后做选择。例如上面\(F=F_{1} \land F_{2}\),并且\(F_{1}\)中只涉及\(E_{1}\)中的属性,\(F_{2}\)中涉及\(E_{1}\)和\(E_{2}\)中的属性
(7)选择与并的分配律
\[\sigma(E_{1} \cup E_{2}) \equiv \sigma_{F}(E_{1}) \cup \sigma_{F}(E_{2})
\]
- 假设:\(E=E_{1} \cup E_{2}\),\(E_{1}\)和\(E_{2}\)有相同的属性名
(8)选择与差运算的分配律
\[\sigma(E_{1} - E_{2}) \equiv \sigma_{F}(E_{1}) - \sigma_{F}(E_{2})
\]
(9)选择对自然连接的分配律
\[\sigma_{F}(E_{1} \bowtie E_{2}) \equiv \sigma_{F}(E_{1}) \bowtie \sigma_{F}(E_{2})
\]
- \(F\)只涉及\(E_{1}\)和\(E_{2}\)的公共属性
(10)投影与笛卡尔积的分配律
\[\Pi_{A_{1},A_{2},...,A_{n},B_{1},B_{2},...,B_{m}}(E_{1}×E_{2}) \equiv \Pi_{A_{1},A_{2},...,A_{n}}(E_{1}) × \Pi_{B_{1},B_{2},...,B_{m}}(E_{2})
\]
- \(A_{1},A_{2},...,A_{n}\)是\(E_{1}\)的属性
- \(B_{1},B_{2},...,B_{m}\)是\(E_{2}\)的属性
(11)投影与并的分配律
\[\Pi_{A_{1},A_{2},...,A_{n}}(E_{1} \cup E_{2}) \equiv \Pi_{A_{1},A_{2},...,A_{n}}(E_{1}) \cup \Pi_{A_{1},A_{2},...,A_{n}}(E_{2})
\]
二:查询树的启发式优化
- 这是对关系代数表示的查询树进行优化的方法
(1)典型的启发式规则
典型的启发式规则
- 【规则1】选择运算应尽可能先做:这是为了减少中间结果的规模
- 【规则2】投影和选择运算同时进行:这是为了避免重复扫描
- 【规则3】将投影运算与其前后的双目运算结合起来:这是为了避免重复扫描
- 【规则4】把某些选择运算和其前面的笛卡尔积结合起来成为一个连接运算:这是为了减少中间结果的规模
- 【规则5】提取公共子表达式(公因子):这是为了保存计算结果,避免重复计算
(2)实现算法
- 该算在遵循启发式规则,并应用关系代数表达式等价变换规则来优化关系表达式
- 该算法的输入和输出都是查询树(分别对应待优化和优化的关系表达式)
算法步骤
- 【步骤1】分解选择运算:这是为了便于不同的选择运算沿树的不同分枝向树叶移动,一直移动到与这个选择条件相关的关系处,使选择尽可能先做。\(\sigma_{F_{1} \land F_{2} \land ... \land F_{n}} (E)\Rightarrow \sigma_{F_{1}}(\sigma_{F_{2}}(...(\sigma_{F_{n}}(E))...))\)
- 【步骤2】通过交换选择运算,将每个选择运算尽可能移动到叶端:利用规则4~9尽可能把选择移动到树的叶端
- 【步骤3】通过交换投影运算,将每个投影运算尽可能移动到叶端:利用规则3、11、10、5尽可能把投影移动到树的叶端
- 【步骤4】合并选择和投影的串接:利用规则3~5把选择和投影的串接合并成单个选择、单个投影或一个选择后面跟一个投影。这是为了使多个选择或投影能同时进行,或在一次扫描中全部完成
- 【步骤5】对内结点分组:每一双目运算(\(×\)、\(\bowtie\)、\(\cup\)、\(-\))和它所有的直接祖先的一元运算结点(\(\sigma\)或\(\Pi\))分为一组(如果其后代直到叶子全是单目运算,则也将他们并入该组);注意当双目运算是笛卡尔积(\(×\)),而且其后的选择不能与它结合为等值连接时,则不能将选择与这个\(×\)并为一组
(3)实例演示
- 注意这是一个很重要的考点
【例】如下给出了一个SQL语句
SELECT Student.Sname FROM Student,SC
WHERE Student.Sno=SC.Sno AND SC.Sno='2';
将SQL语句转为关系代数表达式
- 先对
Student和SC做笛卡尔积 - 再对中间结果做选择(条件为
Student.Sno=SC.Sno) - 再对中间结果做选择(条件为
SC.Sno='2') - 最后投影
结果为
\[\Pi_{Sname}(\sigma_{Student.Sno=sc.Cno \land sc.cno=2}(student × sc))
\]
将关系代数表达式转为查询树
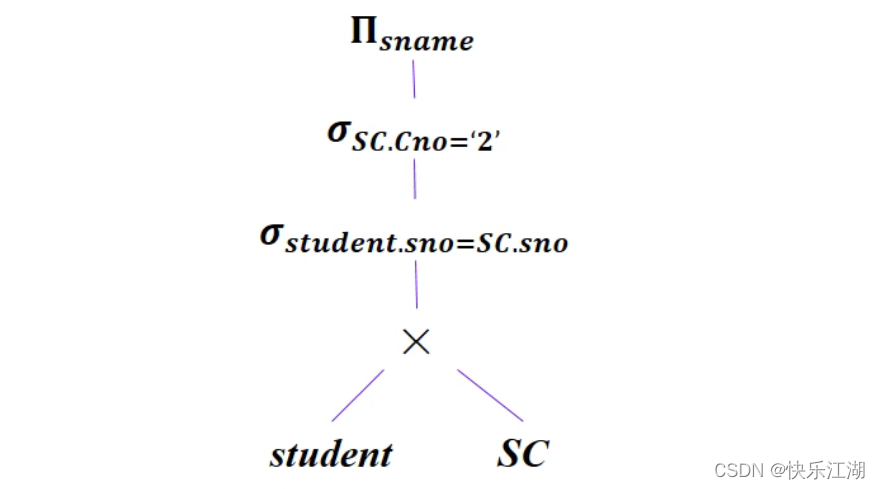
查询树优化
①首先选择条件尽可能下移:
SC.Sno='2'只和SC有关,所以它会沿着分支恰当的分支下移到SC的上方Student.Sno=SC.Sno同时涉及Student和SC,所以只能待在那里
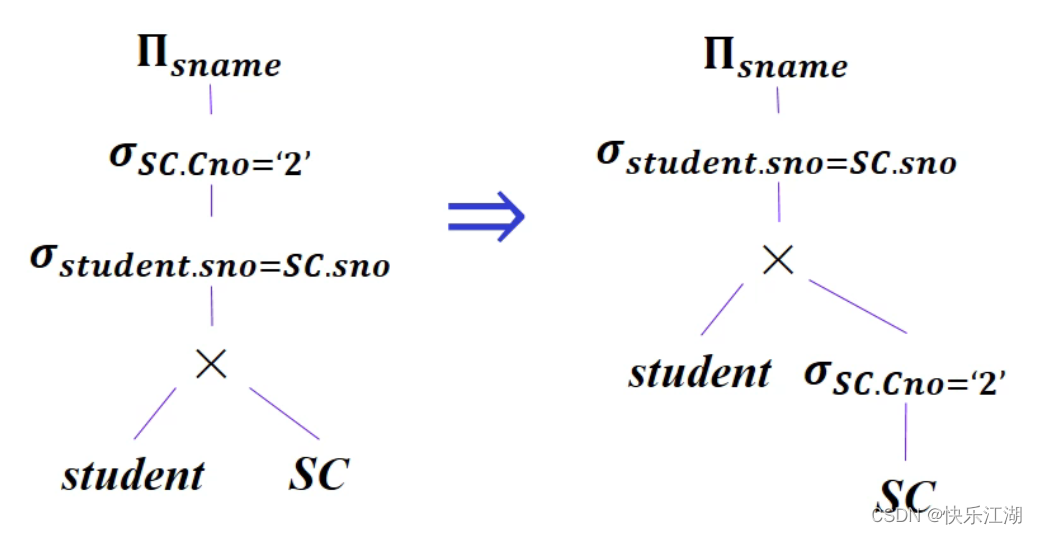
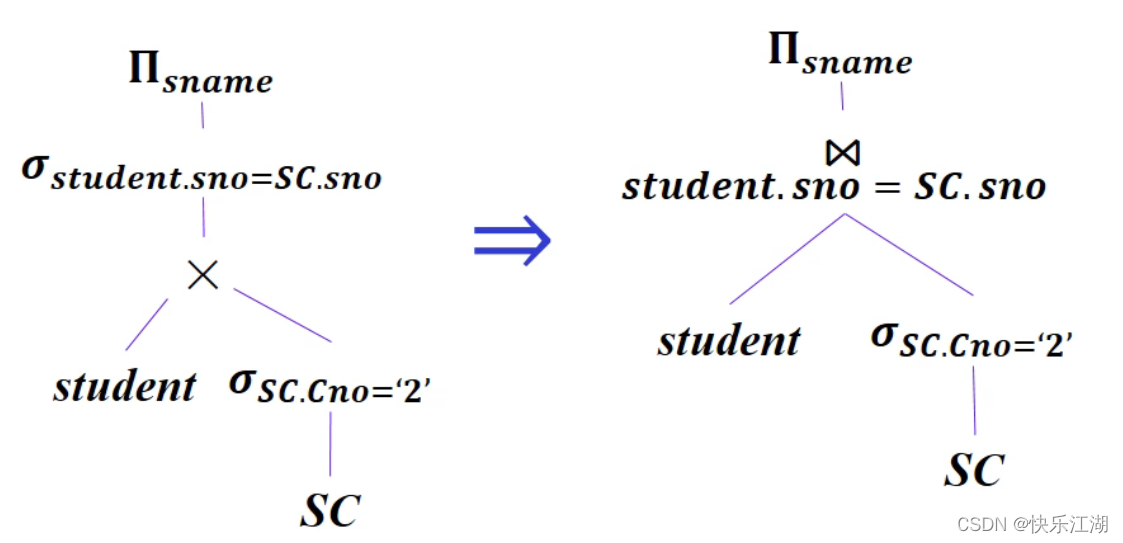
②:把选择和其之前的笛卡尔积合并为等值连接,或者干脆变为自然连接
【例】查询选修了数据库课程的女生学号与姓名,如下是SQL语句
SELECT Student.Sno,Sname FROM Student,SC,Course
WHERE Cname='datebase' AND Ssex='女';
将SQL语句转为关系代数表达式
\[\Pi_{Sno,Sname}(\sigma_{Cname='数据库' \land Ssex='女'}(SC \bowtie Course \bowtie Student))
\]
将关系代数表达式转为查询树
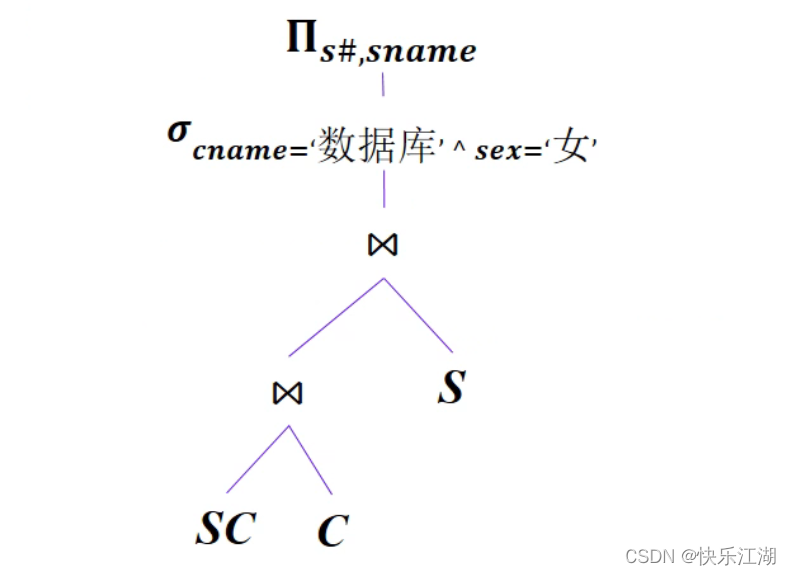
查询树优化
①:选择条件复杂,先分解选择条件
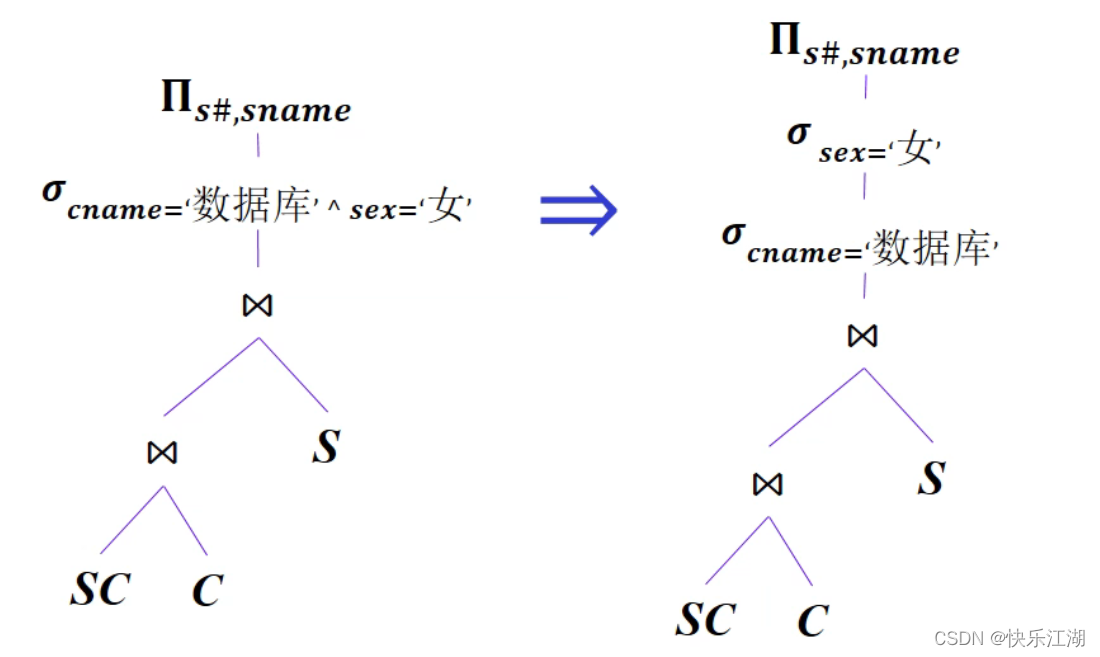
②:将选择运算尽可能移动到树的叶端
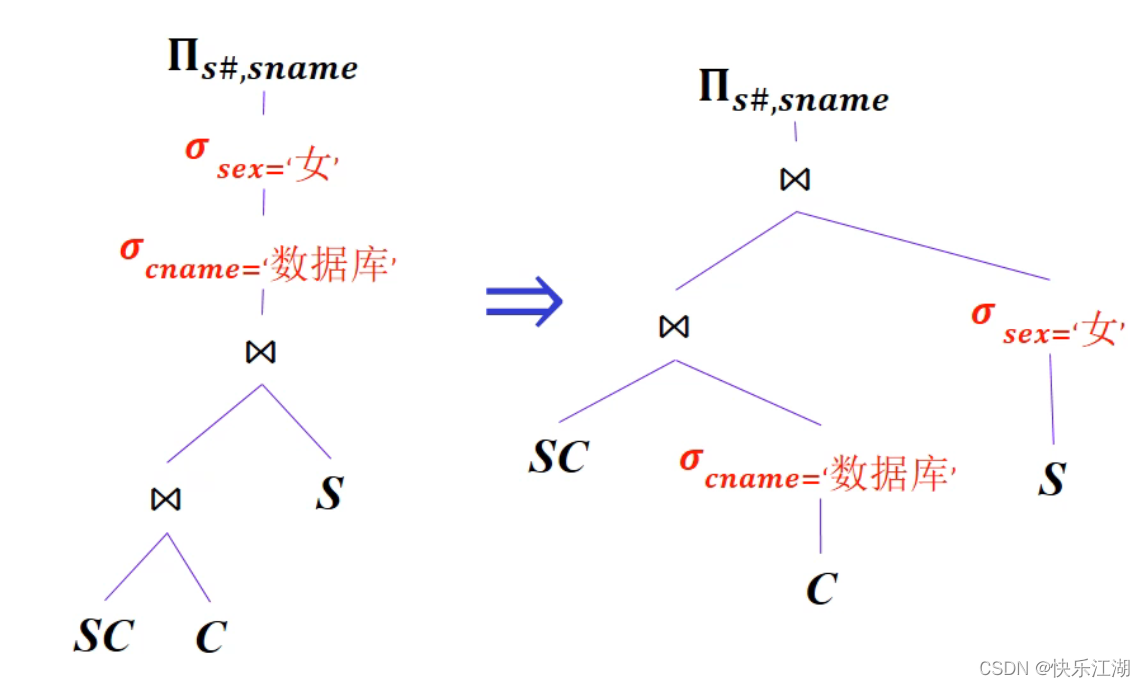
③:涉及了投影运算,所以也把它尽可能移动到树的叶端
- 投影运算下移时要保留连接属性
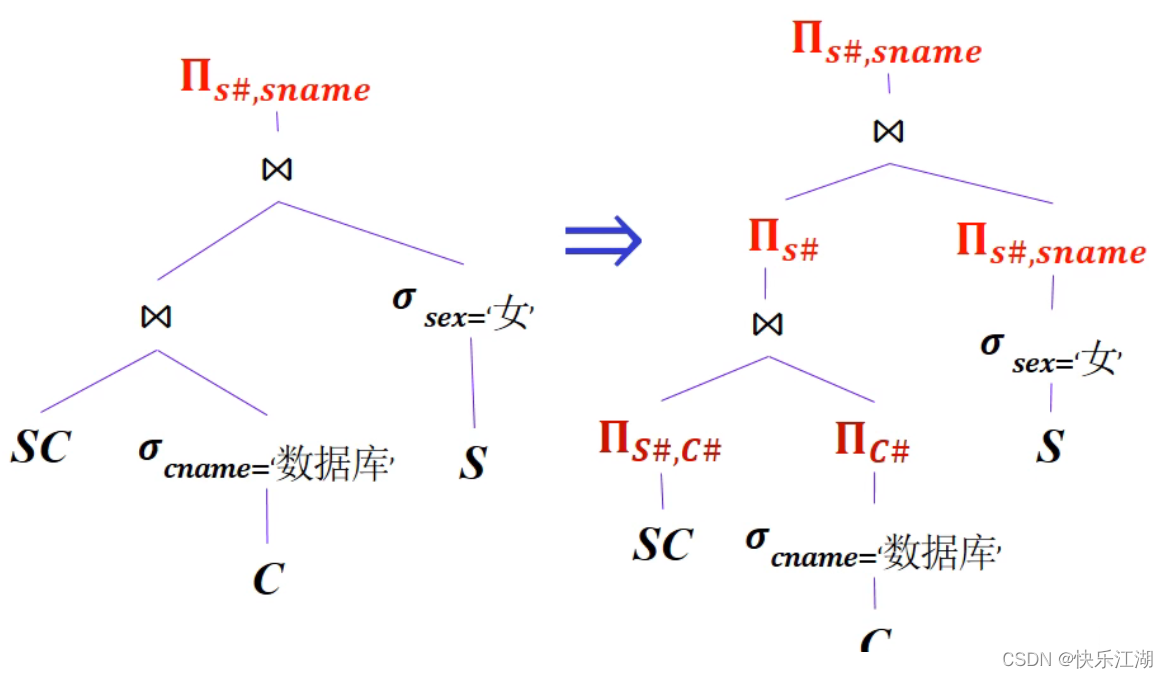
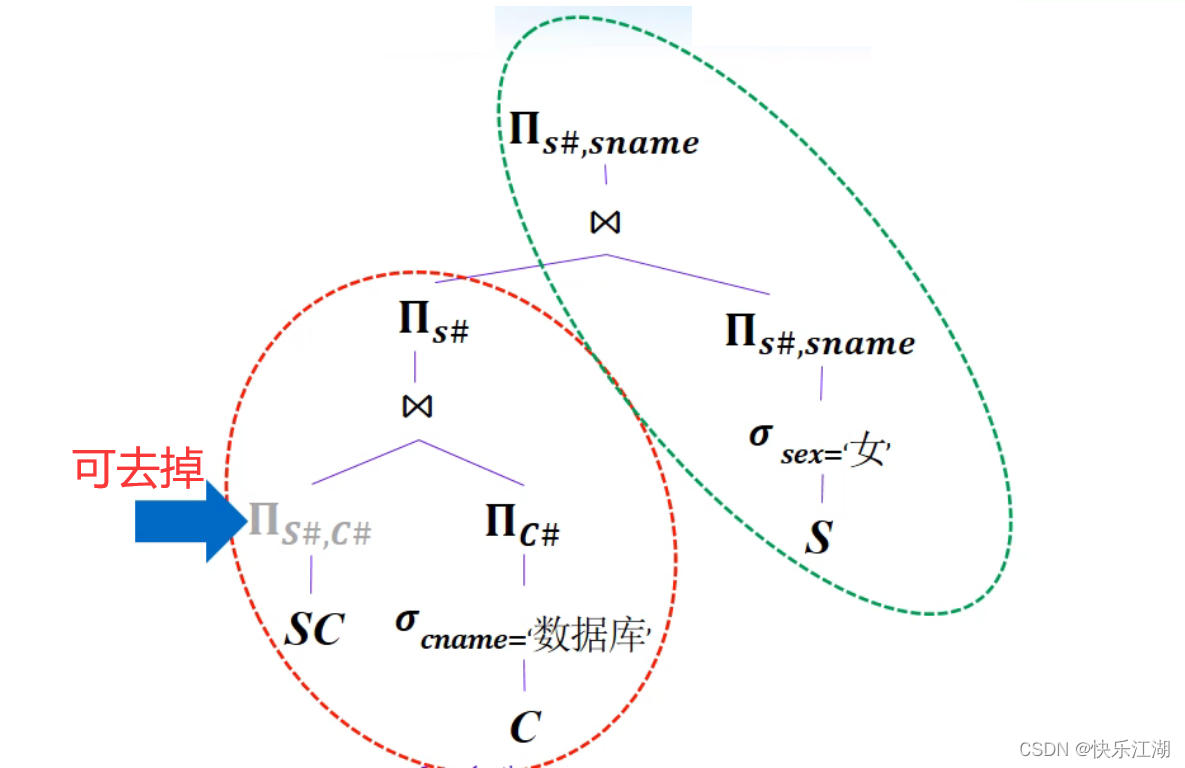
④:对内结点进行分组




 浙公网安备 33010602011771号
浙公网安备 33010602011771号