
一:查询优化概述
(1)查询优化的地位和重要性
关系系统的查询优化既是关系数据库管理系统实现的关键技术,又是关系系统的优点所在。用户只要提出“干什么”,而不必指出“怎么干”。
在非关系系统中,用户必须了解存取路径,系统提供用户选择存取路径的手段,查询的效率由用户的存取策略决定,且系统是无法加以优化的。这就要求用户需要具有较高的数据库技术和程序设计水平
查询优化的优点不仅在于用户不必考虑如何最好地表达查询以获得较高的效率,而且在于系统可以比用户程序的“优化”做得更好。这是因为:
- 优化器可以从数据字典中获得很多统计信息,但是用户程序难以获得
- 即便数据库物理统计信息改变,系统也可以进行优化从而选择相应的执行计划,但是对于非关系系统则必须要重写程序
- 优化器可以考虑数百种不同的执行计划,但程序员一般仅能考虑有限的几种可能性
- 优化器包含了很多复杂的优化技术,这样就等同于所用的使用者间接拥有了这些技术
(2)执行代价
目前关系数据库管理系统通过某种代价模型计算出各种查询执行策略的执行代价,然后选取代价最小的执行方案。一般来说:总代价=I/O代价+CPU代价+内存代价+通信代价
- 计算查询代价时一般用查询处理读写的块数作为衡量单位
二:一个例子
可以通过“求选修了2号课程的学生姓名”这样一个例子来说明为什么要进行查询优化
以下是一些系统假设
-
假定学生-课程数据库中有1 000个学生记录,10 000个选课记录(平均每一个学生了选了10门课),其中选修2号课程的选课记录为50个
-
有7个内存块(其中分配5块用于装入
Student表,1块用于装入SC表,1块用于装入中间结果) -
其中一块可以装入10个
student元组(或10个student与SC笛卡尔积元组);一块也可以 装入50个SC元组(因为SC的列数较少) -
连接方法为:基于数据块的嵌套循环法。
-
之所以这样分配的原因:因为嵌套循环算法需要选用占用内存少的表作为外表,student表有1000行,每块装10行,所以需要100块;SC表有10000行,每块装50行,所以需要200块。
-
由于student表需要100个内存块,而分配给它的只有5个,所以不可能一次全部装入内存,每次只能装入一部分,比较完了再装入另外一部分。每换一批数据,内标就需要全部重新装入以便,所以为了减少内表循环装入的次数,就必须尽可能的分配内存给外表
-
连接后的元组装满一块后就写到中间文件上
SELECT Student.name
FROM Student,SC
WHERE Student.Sno=SC.Sno AND SC.Cno='2';
系统可以用多种等价的关系代数表达式来完成这一查询,这里只举三种情况
(1)情况1

Student与Sc作笛卡尔积,而后作行选择运算(选择条件为Student.Sno=SC.Sno AND SC.Cno='2'),最后进行投影操作
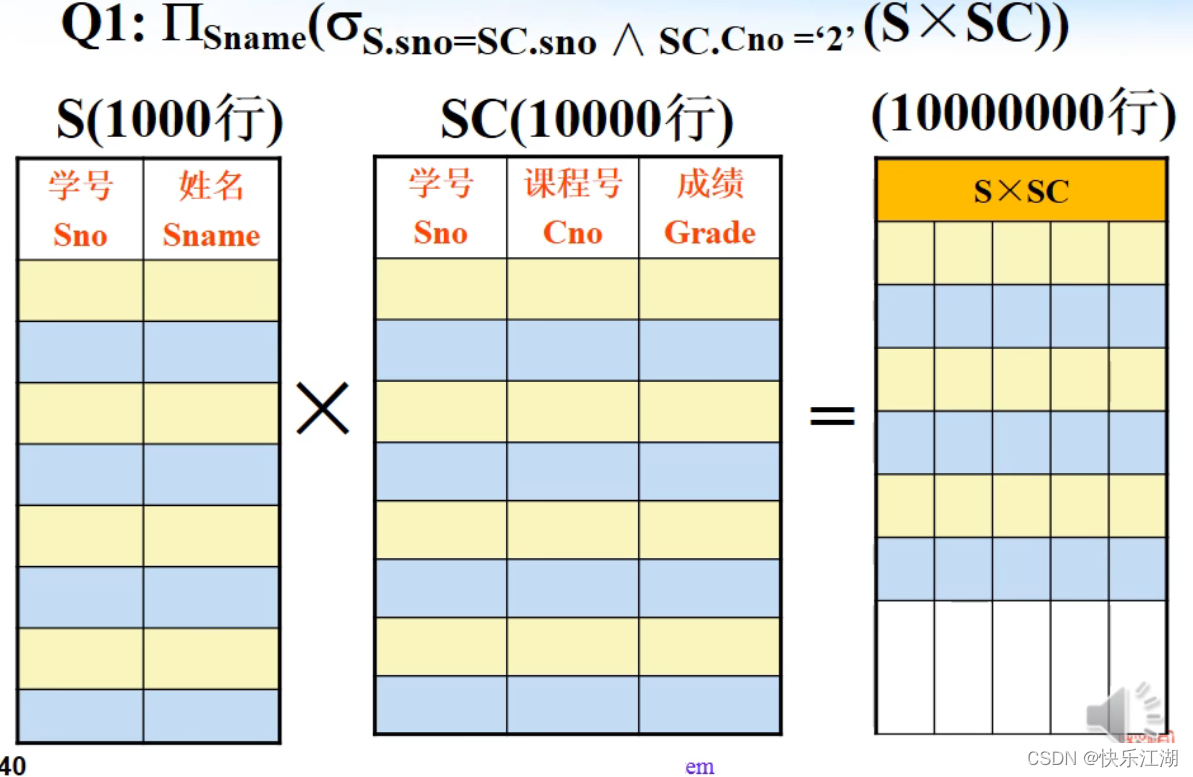
①:计算广义笛卡尔积
操作:
- 在内存中尽可能多地装入某个表(如
Student表)的若干块,留出一块存放另一个表(如SC表)的元组; - 然后把
SC中的每个元组和Student中每个元组连接,连接后的元组装满一块后就写到中间文件上,再从SC中读入一块和内存中的Student元组连接,直到SC表处理完; - 这时再一次读入若干块
Student元组,读入一块SC元组,重复上述处理过程,直到把Student表处理完
块数:
- 读一遍
Student表所需块数为=\(\frac{1000}{10}=100\)块 - 读一遍
SC表所需要块数为=\(\frac{10000}{50}=200\)块 - 由于
Student表可用块数为5块,所以分\(\frac{100}{5}=20\)次读入 - 同时,
Student表的每一部分读入内存时,SC表都需要重新读一遍,以此完成与Student表的连接。所以需要读入200×20=4000块 - 所以笛卡尔积读取总块数为100+4000=4100块
Student表和SC表作笛卡尔积共有\(10^{7}\)行,每块装10行,所以中间结果块数为\(10^{6}\)块(写入)
②:作选择操作
块数:
- 所读块数为\(10^{6}\)块
- 选择后的结果只有50个(无需读写)
③:作投影操作
- 无需读写
情况1读取总块数:
4100(读)+\(10^{6}\)(写)+\(10^{6}\)(读)。约为200万块
(2)情况2
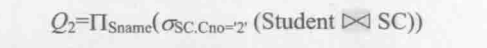
Student与Sc作自然连接,而后作行选择运算(选择条件为Student.Sno=SC.Sno AND SC.Cno='2'),最后进行投影操作
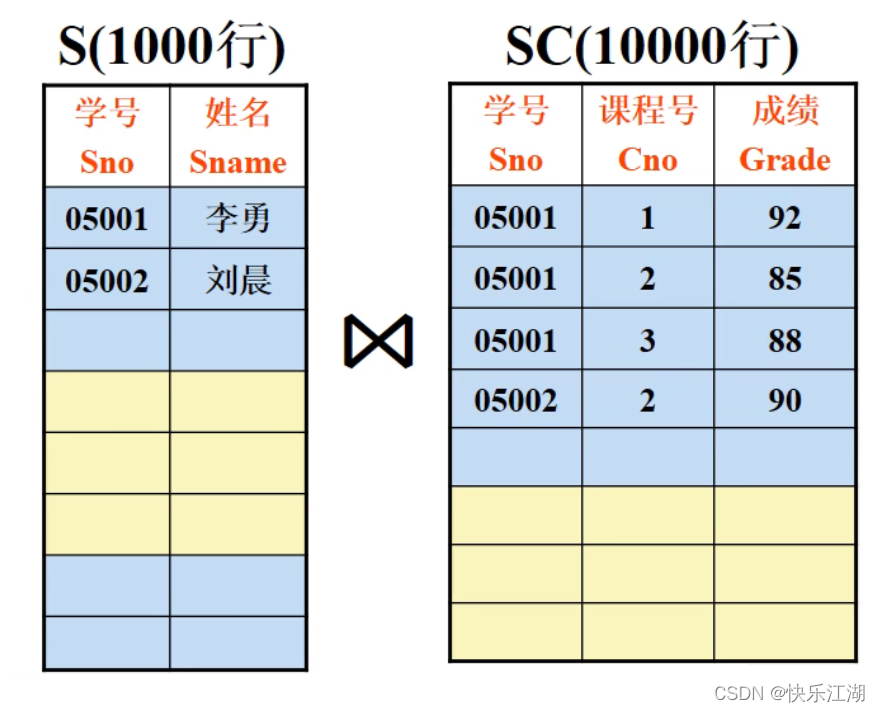
①:计算自然连接
块数:
- 首先读
Student和SC,与情况1一致。因此总块数=4100块 Student和SC自然连接后右10000行,所以中间结果块数\(\frac{10000}{10}\)=1000块
②:作选择操作
块数:
- 读入中间结果,块数=1000块
③:作投影操作
- 50个结果可以不用写入
情况2读取总块数:
4100(读)+\(1000\)(写)+\(1000\)(读)。共计6100块
- 代价约为情况1的\(\frac{1}{488}\)
(3)情况3

首先Sc作行选择(选择条件为SC.Cno='2'),而后作自然连接运算,最后进行投影操作
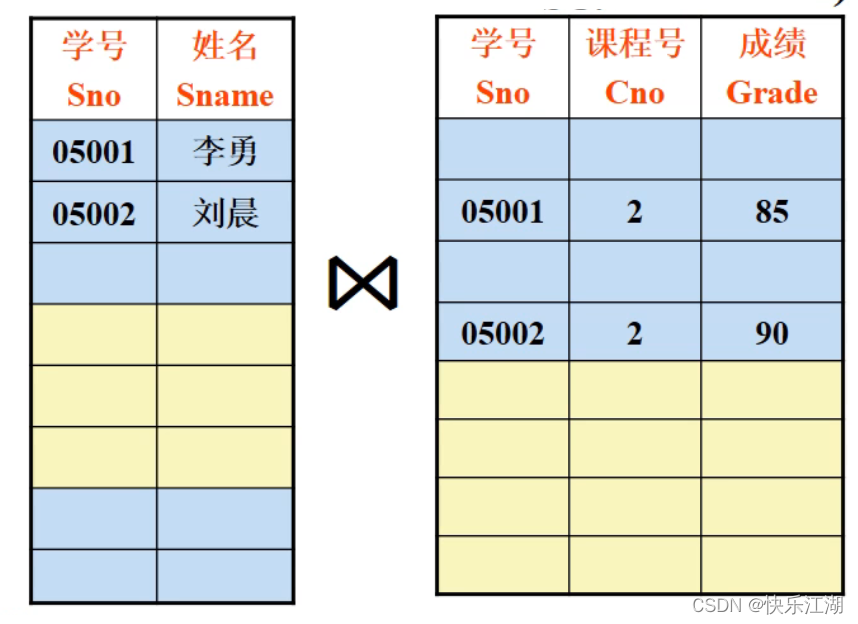
块数:
- 先对
SC表作选择操作,只需读一遍SC表,存取块数为100块,因为满足条件的元组仅50个,不必使用中间文件 - 读取
Student表,把读入的Student元组和内存中的SC元组作连接。也只需读一遍Student表,共100块,把连接结果投影输出
情况3读取总块数:
100(读)+200(读)。共计300块
- 代价约为情况1的的万分之一
- 代价约为情况2的\(\frac{1}{20}\)
三:代数优化和物理优化
通过上面的那个例子可以看到:经过优化,磁盘I/O涉及块数从200万下降至300,效率提升显著,这说明查询优化是非常有必要的。上述三种情况其有些操作是可以优化的,例如
- 情况一:明知在笛卡尔积后要做行选择,那为什么不在连接时就把选择做了,这样只会留下50个元组,也即省去了100万个块的读写操作
- 情况二:也是如此,在作自然连接时如果也把选择做了,就会省去1000个块的读写操作
- 情况三:它是先作选择再作连接,所以大大减少了块数
因此,由情况1到情况2再到情况3这样的优化称之为代数优化;而如果对底层路径或算法进行优化则称之为物理优化。例如对于情况三,可以添加索引,继续减小代价



