一:关系代数的基本概念
关系代数:是一种抽象的查询语言,用于对关系运算来表达查询
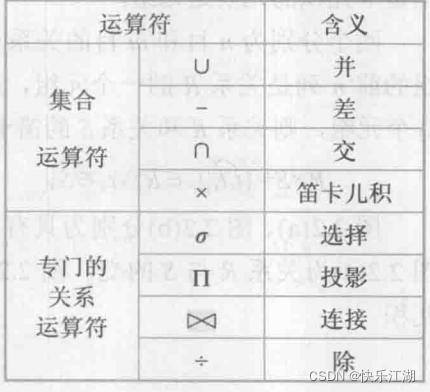
关系代数的运算对象和运算结果都是关系,所用到运算符可分为如下两种
- 传统的集合运算:运算从行的角度进行
- 专门的关系运算:运算同时涉及行和列
二:传统的集合运算
严格的定义这里不再给出,可借助课本。我的目的就是能帮助快速理解即可
(1)并(union)
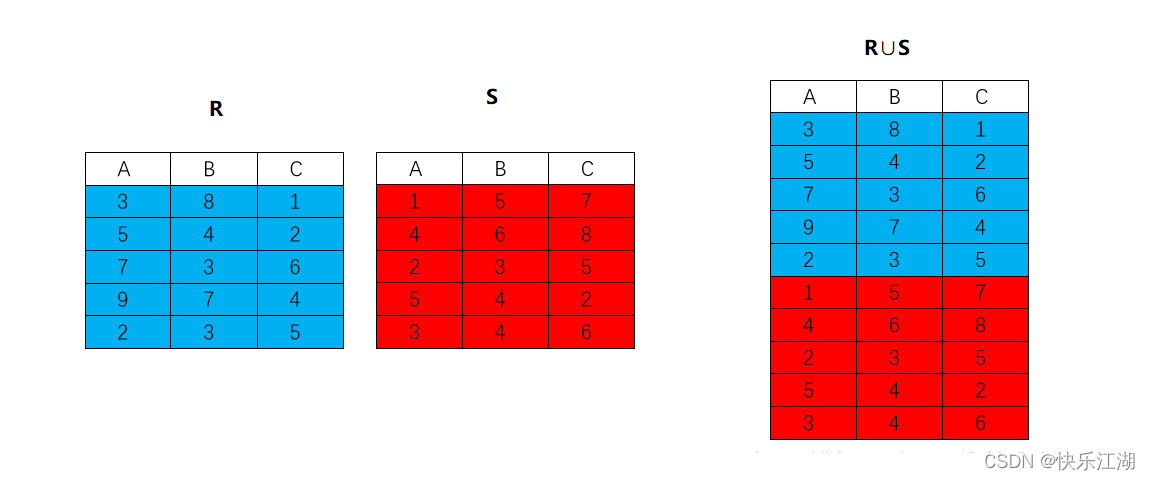
并:对于关系\(R\)和\(S\),并操作就是将两个关系上下拼在一起形成一个新的关系,记为\(R\)∪\(S\)
- 所以两个关系具有相同数目的属性
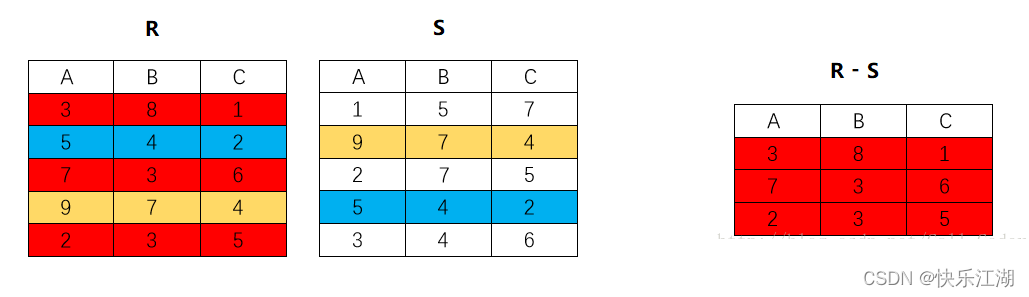
(2)差(except)
差:对于关系\(R\)和\(S\),求他们的差,就是在\(R\)中去掉两个关系中所有相同的行,形成一个新的关系,记为\(R\)-\(S\)
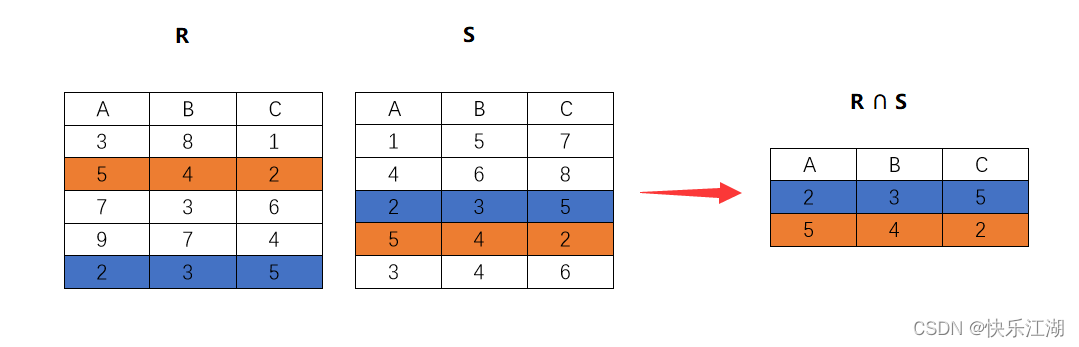
(3)交(intersection)
交:对于关系\(R\)和\(S\),求他们的交,就是选出两个关系中所有相同的行,形成一个新的关系,记为\(R\)∩\(S\)
- 所以\(R\)∩\(S\)=\(R\)-\((R-S)\)
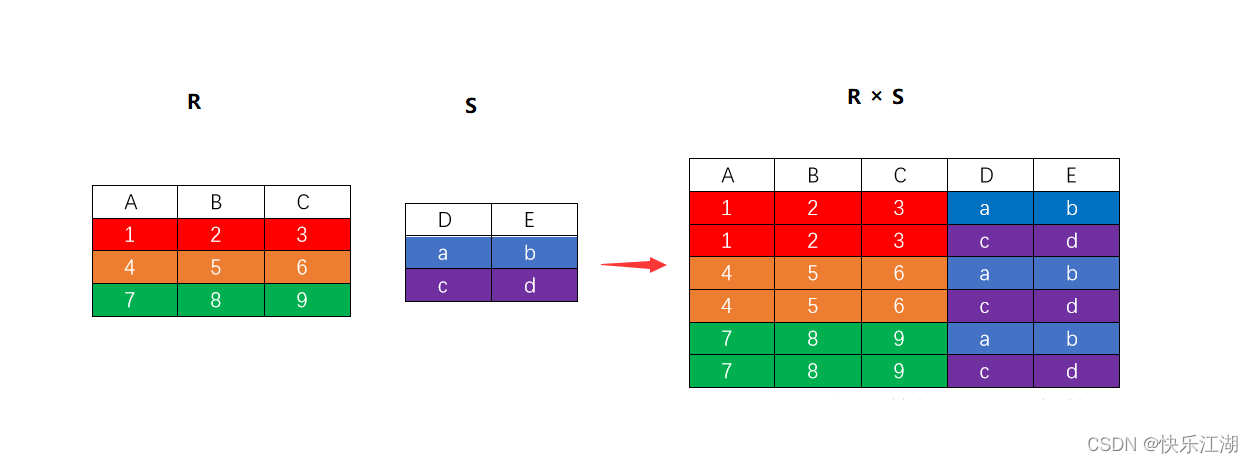
(4)笛卡尔积(cartersian product)
笛卡尔积:对于关系\(R\)和\(S\),求他们的笛卡尔积,就是两个关系所有元组的不同排列组合,形成一个新的关系,记为\(R\)×\(S\)
三:专门的关系运算
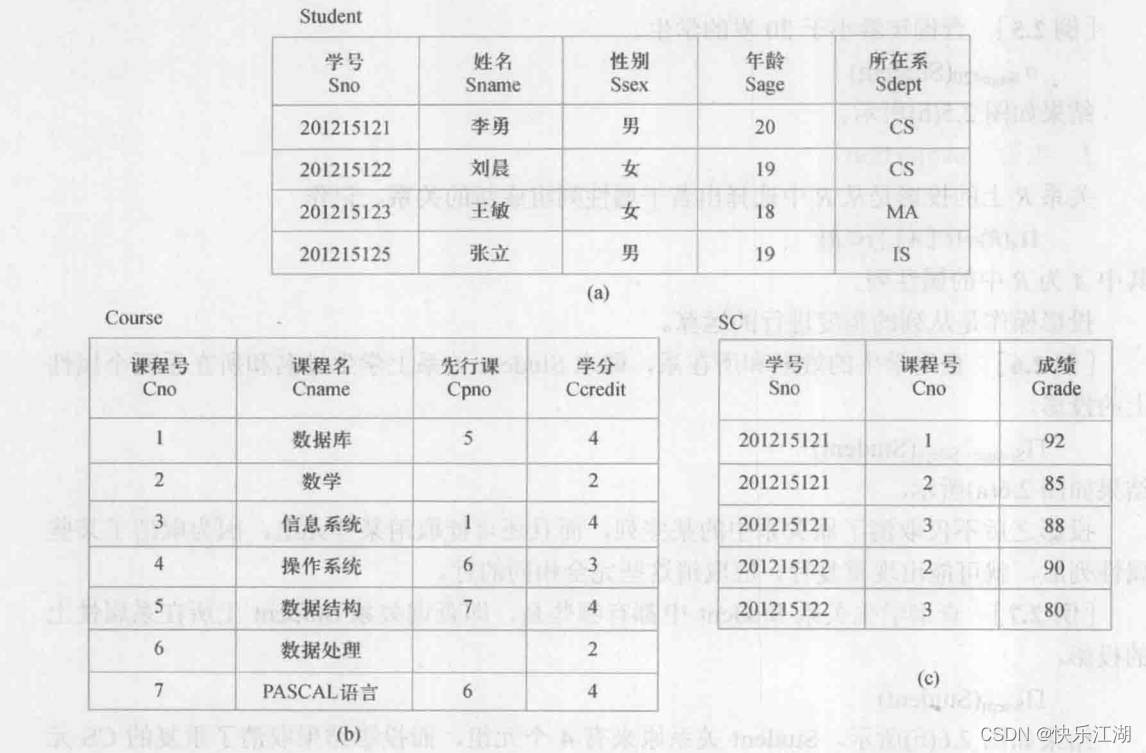
注意:在下面的叙述中有时会用到如下三种关系
- 学生关系Student
- 课程关系Course
- 选修关系SC
(1)选择(selection)
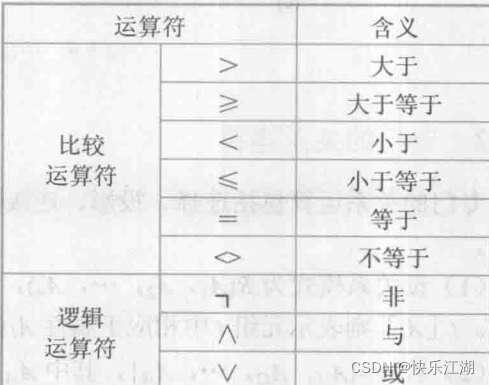
选择:从行的角度出发,在关系\(R\)中选择满足条件的元组然后组成新的关系。“满足条件”意味着有条件表达式,其运算符如下
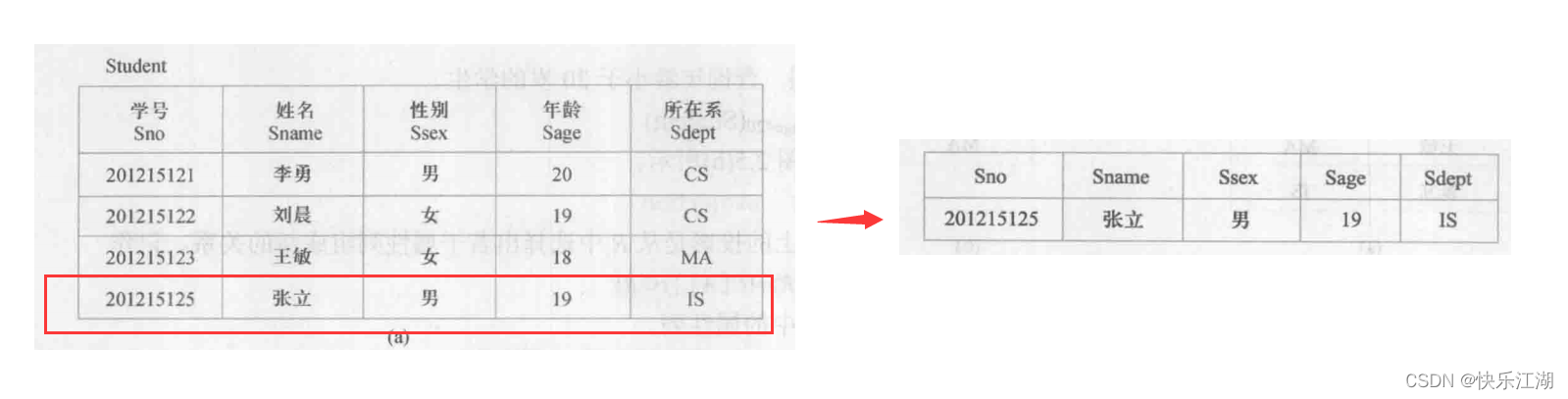
例如可在关系Student中查询所有IS系的学生,查询结果形成一个关系,记为\(σ_{Sdept=_{'IS'}}(Student)\)
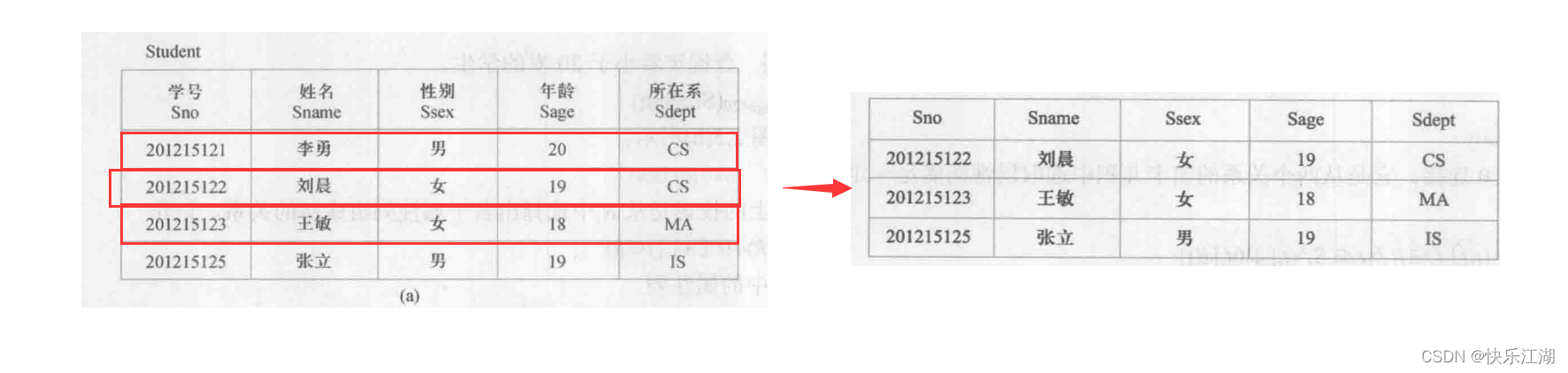
再比如可在关系Student中查询所有年龄小于20的学生,查询结果形成一个关系,记为\(σ_{Sage<20}(Student)\)
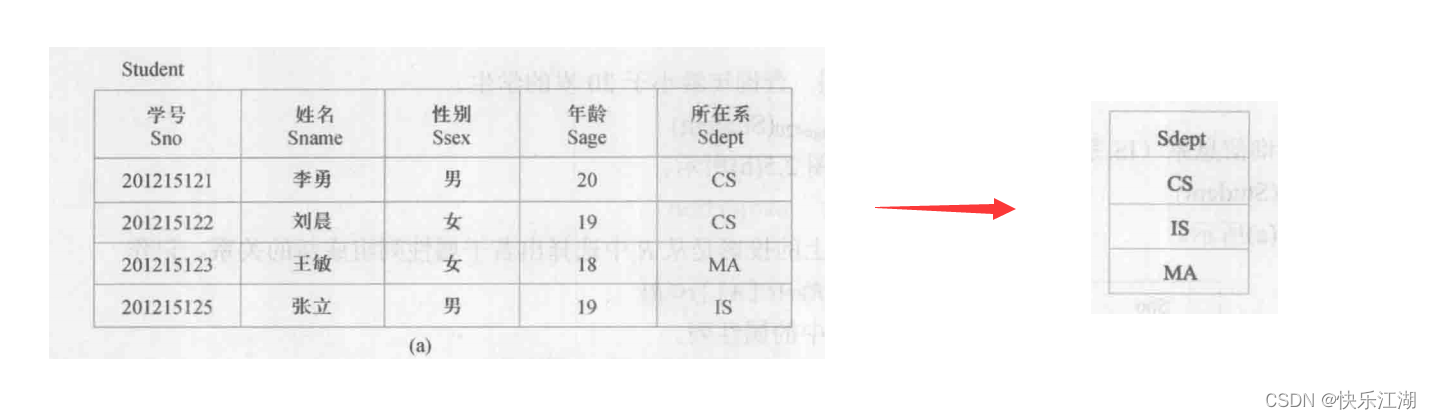
(2)投影(projection)
选择:从列的角度出发,选择满足条件的若干属性列组成新的关系
- 投影之后取消了原关系中的某些列,当然也有可能会取消某些元祖(因为一旦取消了某些属性列后就极有可能出现重复行),所以一定注意消除完全相同的行
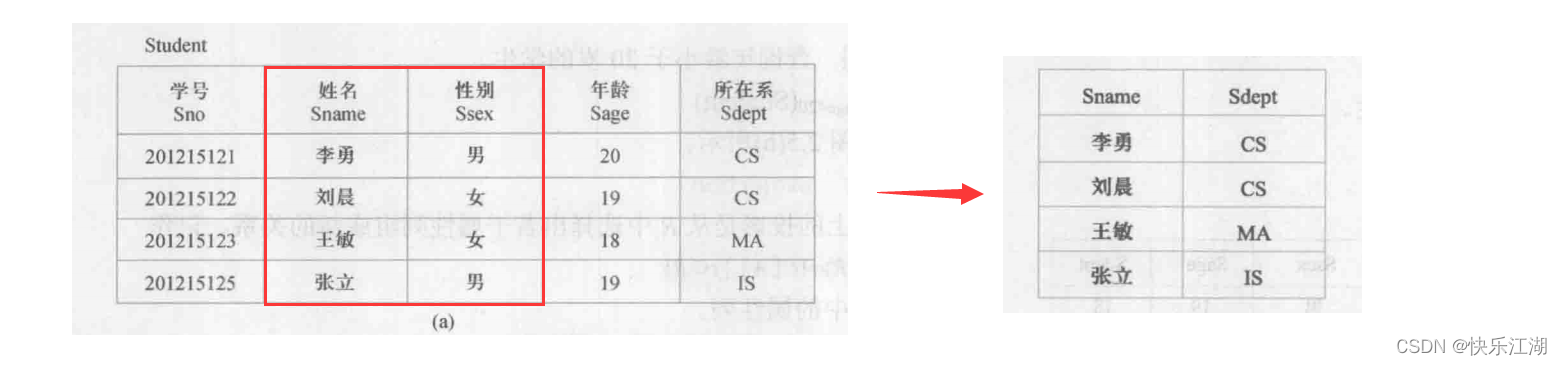
例如在关系Student中查询姓名和所在系的投影,记为\(∏_{Sname,Sdept}(Student)\)
再比如在关系Student中查询都有哪些系,记为\(∏_{Sdept}(Student)\)
- 注意投影要取消重复的CS元组
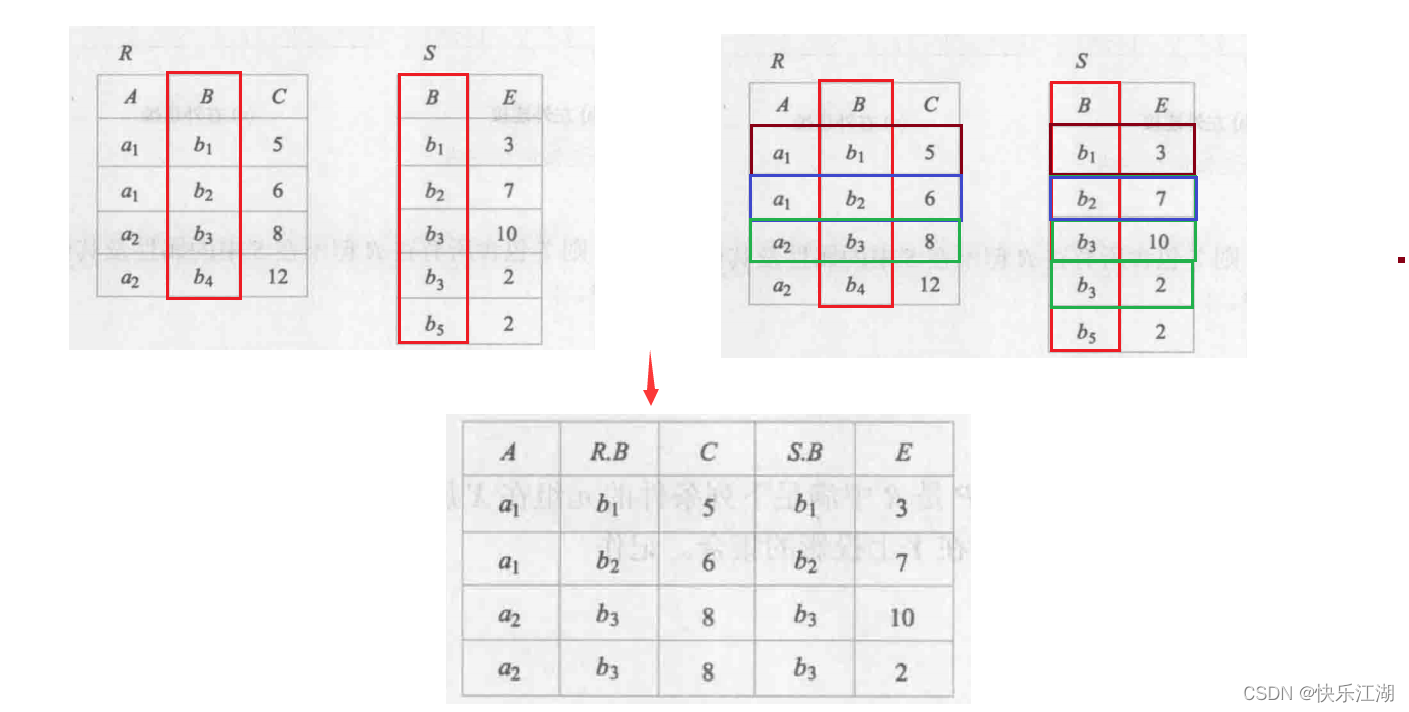
(3)连接(join)
A:等值连接和自然连接
等值连接:可以按照如下步骤考虑,最终形成新的关系,记为
- 首先找到关系\(R\)和\(S\)中属性相同的列
- 然后找到两列中相同的元素
- 将相同元素所在的行组成新的一行,需要用【关系.属性】的格式区两个关系中相同的属性
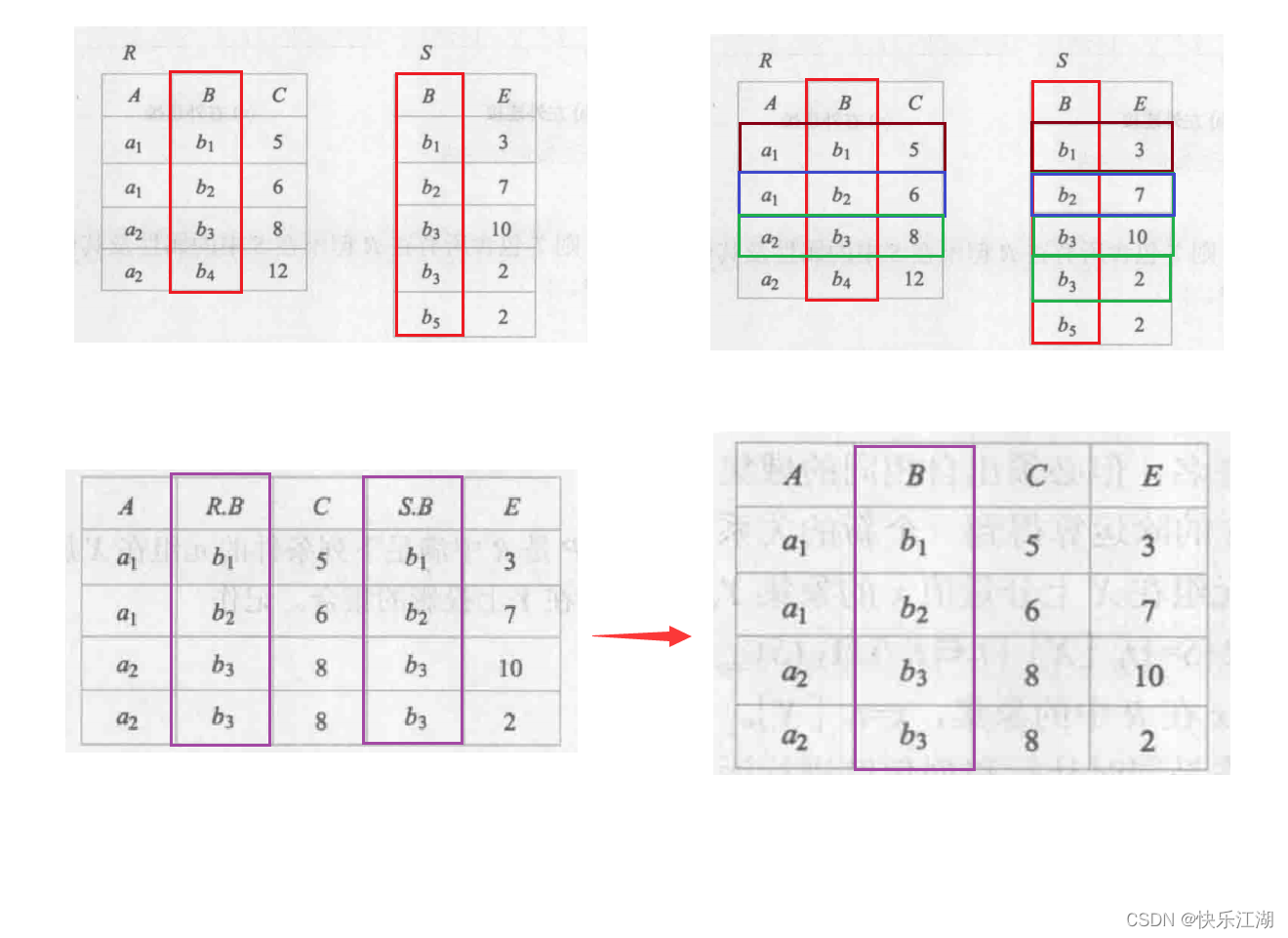
自然连接:它是一种特殊的等值连接,在等值连接的结果中去掉重复列即可
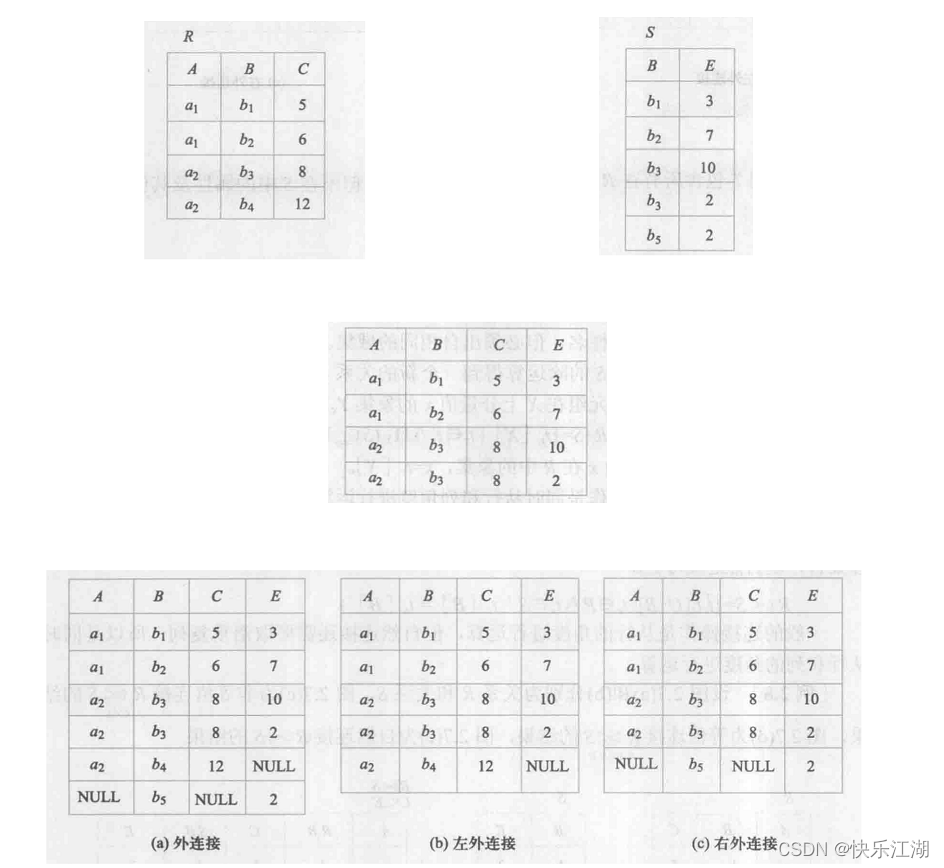
B:外连接
悬浮元组的概念:\(R\)和\(S\)在做自然连接时,\(R\)中某些元组有可能在\(S\)中不存在公共属性上值相等的元组,就会造成\(R\)中这些元组在操作时被舍弃(反过来\(S\)也是这样)。例如上图自然连接中就舍弃了\(R\)的第4个元组和\(S\)的第5个元组
外连接:若将悬浮元组保留在自然连接的结果中,而在其他属性上填NULL,那么这种连接就叫做外连接,同时
- 左外连接:只保留左边关系\(R\)中的悬浮元组
- 右外连接:只保留右边关系\(R\)中的悬浮元组
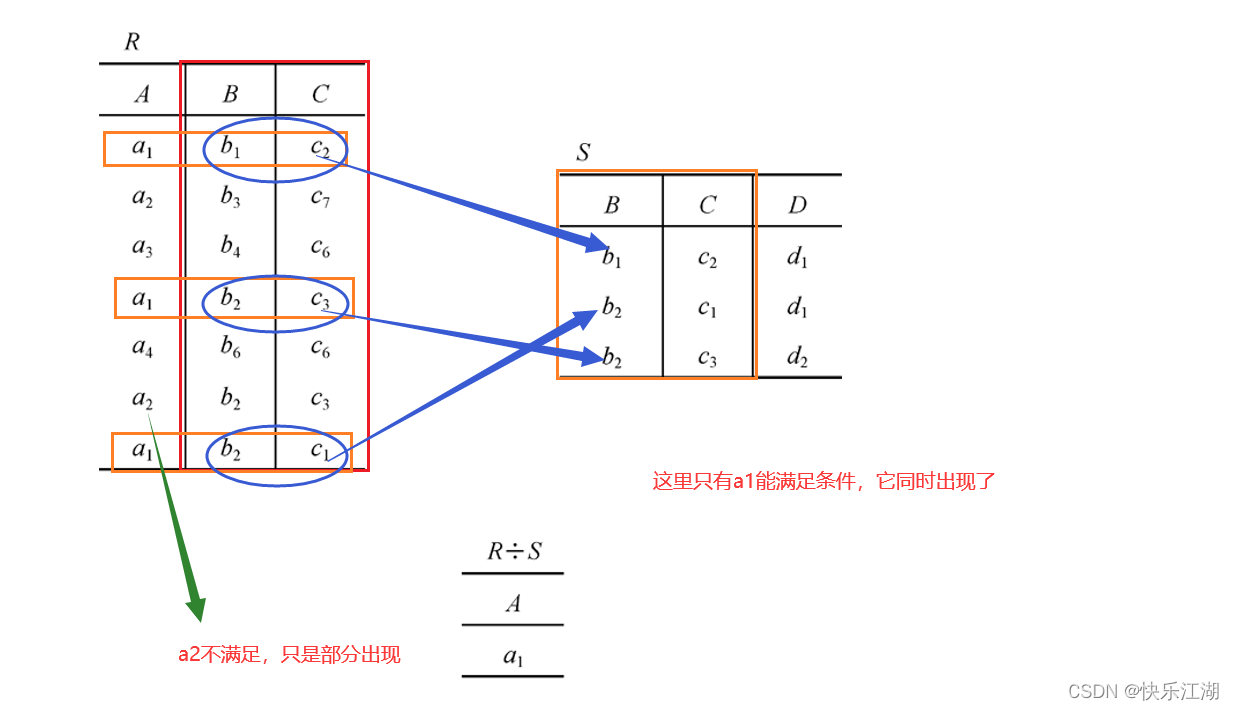
(4)除(division)
除:是笛卡尔积的逆运算,对于关系\(R\)和\(S\),求\(R\)÷\(S\)可按如下步骤考虑
- 研究对象是\(R\)和\(S\)中相同的属性列
- 在\(R\)中挑选元祖,所挑选的元组一定满足它的属性均出现在\(S\)对应相同属性列的所有属性集合内