DiffSeq

目录

• 概
• 符号说明
• 流程
• 代码

 

Gong S., Li M., Feng J., Wu Z. and Kong L. DiffuSeq: Sequence to sequence text generation with diffusion models. In International Conference on Learning Representations (ICLR), 2023

概

本文提出了一种用于 Seq2Seq 的不需要 classifier 引导的扩散模型, 且是在连续空间上讨论的.
虽然方法看起来很简单, 但是感觉很容易 work 和推广.

符号说明

• ${\mathrm{z0\sim q(z)z0\sim q(z),\; a\; real-world\; data\; distribution;}}^{}$
• ${\mathrm{zT\sim N(0,I)zT\sim N(0,I),\; Gaussian\; noise;}}^{}$
• $\mathrm{q(zt|zt-1)=N(zt;\surd 1-\beta tzt-1,\beta tI),t\in [1,2,\dots ,T]q(zt|zt-1)=N(zt;1-\beta tzt-1,\beta tI),t\in [1,2,\dots ,T];}$
• ${\mathrm{f\theta f\theta ,\; a\; diffusion\; model;}}^{}$
• ${\mathrm{wx=[wx1,\dots ,wxm]wx=[w1x,\dots ,wmx],\; m-length\; soure\; sequence\; (离散的);}}^{}$
• ${\mathrm{wy=[wy1,\dots ,wyn]wy=[w1y,\dots ,wny],\; n-length\; soure\; sequence\; (离散的).}}^{}$

流程

• 首先利用获取词的 embeddings:

   

  $${\mathrm{z0=Emb(w)=[Emb(w1),Emb(w2),\dots ],z0=Emb(w)=[Emb(w1),Emb(w2),\dots ],}}^{}$$

   

  这一步实际上是相当于构建从离散空间到连续空间的一个映射:

   

  $${\mathrm{q\varphi (z0|w)=\delta Emb(w)(z0).q\varphi (z0|w)=\delta Emb(w)(z0).}}^{}$$

   

• 因为整个流程设计两个部分: source $\mathrm{xx,\; target yy,\; 不妨令}$

   

  $${\mathrm{x0=Emb(wx)=[Emb(wx1),Emb(wx2),\dots ],y0=Emb(wy)=[Emb(wy1),Emb(wy2),\dots ].x0=Emb(wx)=[Emb(w1x),Emb(w2x),\dots ],y0=Emb(wy)=[Emb(w1y),Emb(w2y),\dots ].}}^{}$$

   

  于是

   

  $${\mathrm{z0=x0\oplus y0.z0=x0\oplus y0.}}^{}$$

   

  类似的之后的 ${\mathrm{ztzt 均可以分为\; source\; 和\; target\; 两部分,\; 即}}^{}$

   

  $${\mathrm{zt=xt\oplus yt.zt=xt\oplus yt.}}^{}$$

   

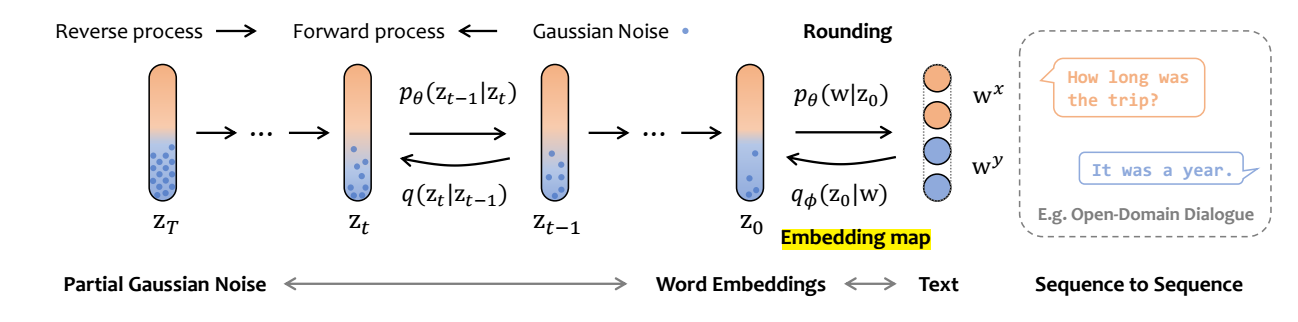
• 前向过程: 如上图所示:

  1. 根据 ${\mathrm{q\varphi (z0|w)q\varphi (z0|w) 得到 z0z0 (这一步实际上是确定的);}}^{}$
  2. 此时我们依旧在连续空间中了, 故我们可以使用一般的高斯分布来加噪, 即:

      

     $${\mathrm{z\prime t\sim q(zt|zt-1)=N(zt;\surd 1-\beta tzt-1,\beta tI).zt\prime \sim q(zt|zt-1)=N(zt;1-\beta tzt-1,\beta tI).}}^{}$$

      

     但是特别地, 我们只对 target 部分加噪:

      

     $${\mathrm{zt=x0\oplus y\prime t.zt=x0\oplus yt\prime .}}^{}$$

      

• 反向过程: 同样如上图所示:

  1. 从标准的高斯分布中采样 ${\mathrm{z\prime TzT\prime ,\; 并令}}^{}$

      

     $${\mathrm{zT=x0\oplus y\prime T.zT=x0\oplus yT\prime .}}^{}$$

      

  2. 根据如下分布进行反向传递:

      

     $${\mathrm{z\prime t-1\sim N(zt-1;\mu \theta (z,t),\sigma \theta (zt,t)),zt-1=x0\oplus y\prime t-1,t\ge 2.zt-1\prime \sim N(zt-1;\mu \theta (z,t),\sigma \theta (zt,t)),zt-1=x0\oplus yt-1\prime ,t\ge 2.}}^{}$$

      

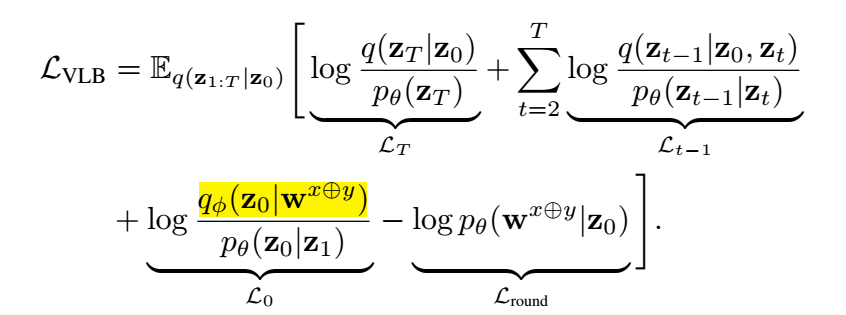
• 最后的损失为如下:

• 需要注意的是, 其中 ${\mathrm{q\varphi (z0|wx\oplus y)q\varphi (z0|wx\oplus y) 本身是一个确定的过程,\; 所以是不提供导数的,\; 可以省略.\; 整体的推导其实普通的\; VLB\; 没什么差别, LroundLround 也只是原来的损失一部分,\; 只是被作者单拎了出来.\; 不过也有道理,\; 因为但看它,\; 其实就是希望训练一个分类网络,\; 将 z0z0 映射回词.}}^{}$

• 不过作者最后用的也不是上面的损失, 而是一个简化的版本 (即把原先的系数给去掉后的结果):

   

  $${\mathrm{LVLB=[T\sum t=2\parallel z0-f\theta (z,t)\parallel 2+\parallel Emb(wx\oplus y)-f\theta (z1,1)\parallel 2-logp\theta (wx\oplus y|z0)]\Rightarrow [T\sum t=2\parallel y0-~f\theta (z,t)\parallel 2+\parallel Emb(wy)-~f\theta (z1,1)\parallel 2-logp\theta (wx\oplus y|z0)].LVLB=[\sum t=2T\Vert z0-f\theta (z,t)\Vert 2+\Vert Emb(wx\oplus y)-f\theta (z1,1)\Vert 2-logp\theta (wx\oplus y|z0)]\Rightarrow [\sum t=2T\Vert y0-f~\theta (z,t)\Vert 2+\Vert Emb(wy)-f~\theta (z1,1)\Vert 2-logp\theta (wx\oplus y|z0)].}}^{}$$

   

• $\mathrm{f,~ff,f~ 就是对 zt,ytzt,yt 的直接拟合,\; 是另一种损失的写法.\; 具体看 here}$

代码

official