Diffusion|DDIM 理解、数学、代码

DIFFUSION 系列笔记|DDIM 数学、思考与 ppdiffuser 代码探索

论文：DENOISING DIFFUSION IMPLICIT MODELS

参考博客open in new window; 参考 aistudio notebook 链接，其中包含详细的公式与代码探索： linkopen in new window

该文章主要对 DDIM 论文中的公式进行小白推导，同时笔者将使用 ppdiffuser 中的 DDIM 与 DDPM 探索两者之间的联系。读者能够对论文中的大部分公式如何得来，用在了什么地方有初步的了解。

本文将包括以下部分：

总结 DDIM。
Non-Markovian Forward Processes：从 DDPM 出发，记录论文中公式推导
探索与思考：
- 验证当 $\eta=1$ DDIMScheduler 的结果与 DDPMScheduler 基本相同。
- DDIM 的加速采样过程
- DDIM 采样的确定性
- INTERPOLATION IN DETERMINISTIC GENERATIVE PROCESSES

DDIM 总览

不同于 DDPM 基于马尔可夫的 Forward Process，DDIM 提出了 NON-MARKOVIAN FForward Processes。（见 Forward Process）
基于这一假设，DDIM 推导出了相比于 DDPM 更快的采样过程。（见探索与思考）
相比于 DDPM，DDIM 的采样是确定的，即给定了同样的初始噪声 $x_t$ ，DDIM 能够生成相同的结果 $x_0$ 。（见探索与思考）
DDIM 和 DDPM 的训练方法相同 ，因此在 DDPM 基础上加上 DDIM 采样方案即可。（见探索与思考）

Forward process

DDIM 论文中公式的符号与 DDPM 不相同，如 DDIM 论文中的 $\alpha$ 相当于 DDPM 中的 $\bar\alpha$ ，而 DDPM 中的 $\alpha_t$ 则在 DDIM 中记成 $\frac {\alpha_t}{\alpha_{t-1}}$ ，但是运算思路一致，如 DDIM 论文中的公式 $(1)-(5)$ 都在 DDPM 中能找到对应公式。
以下我们统一采用 DDPM 中的符号进行标记。即 $\bar\alpha_t = \alpha_1\alpha_2...\alpha_t$

在 DDPM 笔记扩散模型探索：DDPM 笔记与思考open in new window 中，我们总结了 DDPM 的采样公式推导过程为：

x_t\xrightarrow{model} \epsilon_\theta(x_t,t) \xrightarrow {P(x_t|x_0)\rightarrow P(x_0|x_t,\epsilon_\theta)}\hat x_0(x_t, \epsilon_\theta) \\ \xrightarrow {\text{ 推导 }}\mu(x_t, \hat x_0),\beta_t\xrightarrow{P(x_{t-1}|x_t, x_0)}\hat x_{t-1}

而后我们用 $\hat x_{t-1}$ 来近似 $x_{t-1}$ ，从而一步步实现采样的过程。不难发现 DDPM 采样和优化损失函数过程中，并没有使用到 $p(x_{t-1}|x_t)$ 的信息。因此 DDIM 从一个更大的角度，大胆地将 Forward Process 方式更换了以下式子（对应 DDIM 论文公式 $(7)$ ）：

q_\sigma\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \sqrt{\bar\alpha_{t-1}} \mathbf{x}_0+\sqrt{1-\bar\alpha_{t-1}-\sigma_t^2} \frac{\mathbf{x}_t-\sqrt{\bar\alpha_t} \mathbf{x}_0}{\sqrt{1-\bar\alpha_t}}, \sigma_t^2 \mathbf{I}\right)\tag1

论文作者提到了 $(1)$ 式这样的 non-Markovian Forward Process 满足 :

q(x_t|x_0) =N (x_t; \sqrt {\bar \alpha_t} x_0, (1-\bar\alpha_t)I),\bar \alpha_t=\prod_T\alpha_t\tag 2

公式 $(1)$ 能够通过贝叶斯公式：

q(x_t|x_{t-1},x_0) = \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}\tag 3

推导得来。至于如何推导，生成扩散模型漫谈（四）：DDIM = 高观点 DDPMopen in new window 中通过待定系数法给出了详细的解释，由于解释计算过程较长，此处就不展开介绍了。

根据 $(1)$ ，将 DDPM 中得到的公式（同 DDIM 论文中的公式 $(9)$ ）：

x_0 = \frac{\boldsymbol{x}_t-\sqrt{1-\bar\alpha_t} \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}{\sqrt{\bar\alpha_t}}\tag 4

带入，我们能写出采样公式（即论文中的核心公式 $(12)$ ）：

\boldsymbol{x}_{t-1}=\sqrt{\bar\alpha_{t-1}} \underbrace{\left(\frac{\boldsymbol{x}_t-\sqrt{1-\bar\alpha_t} \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}{\sqrt{\bar\alpha_t}}\right)}_{\text {" predicted } \boldsymbol{x}_0 \text { " }}+\underbrace{\sqrt{1-\bar\alpha_{t-1}-\sigma_t^2} \cdot \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}_{\text {"direction pointing to } \boldsymbol{x}_t \text { " }}+\underbrace{\sigma_t \epsilon_t}_{\text {random noise }}\tag 5

其中， $\sigma$ 可以参考 DDIM 论文的公式 $(16)$ ：

\sigma_t =\eta \sqrt {(1-\bar\alpha_{t-1})/(1-\bar\alpha_t)} \sqrt{1-\bar\alpha_t/\bar\alpha_{t-1}}\tag 6

如果 $\eta = 0$ ，那么生成过程就是确定的，这种情况下为 DDIM。

论文中指出， 当 $\eta=1$ ，该 forward process 变成了马尔科夫链，该生成过程等价于 DDPM 的生成过程 。也就是说当 $\eta=1$ 时，公式 $(5)$ 等于 DDPM 的采样公式，即公式 $(7)$ ：

\begin{aligned} \hat x_{t-1}&=\frac 1{\sqrt { \alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon_\theta(x_t,t)) + \sigma_t z\\ &\text{where }z=N(0,I) \end{aligned}\tag 7

将 $(6)$ 式带入到 $(1)$ 式中得到 DDPM 分布公式（本文章标记依照 DDPM 论文，因此有 $\bar \alpha_t=\prod_T\alpha_t$ ）：

\sqrt{1-\bar\alpha_{t-1}-\sigma_t^2} =\frac{1-\bar\alpha_{t-1}}{\sqrt{1-\bar\alpha_t}}\sqrt{\alpha_t} \tag 8

上式的推导过程

\begin{aligned} \frac {\sqrt{1-\bar\alpha_t}}{\sqrt{1-\bar\alpha_t}} \sqrt{1-\bar\alpha_{t-1}-\sigma_t^2} &= \frac{\sqrt{[(1-\bar\alpha_{t-1}-(\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t})(1-\alpha_t)](1-\bar\alpha_t)}}{\sqrt{1-\bar\alpha_t}}\\ &=\frac{\sqrt{(1-\bar\alpha_{t-1})(1-(\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t})(1-\alpha_t))(1-\bar\alpha_{t-1})}}{\sqrt{1-\bar\alpha_t}} \\ &= \frac{\sqrt{(1-\bar\alpha_{t-1})(1-\bar\alpha_t-1+\frac{\bar\alpha_t}{\bar\alpha_{t-1}})}}{\sqrt{1-\bar\alpha_t}}\\ &= \frac{\sqrt{(1-\bar\alpha_{t-1})(1-\bar\alpha_{t-1})\frac{\bar\alpha_t}{\bar\alpha_{t-1}}}}{\sqrt{1-\bar\alpha_t}} \\&=\frac{1-\bar\alpha_{t-1}}{\sqrt{1-\bar\alpha_t}}\sqrt{\alpha_t} \end{aligned}

因此

\begin{aligned} \boldsymbol{x}_{t-1}&=\sqrt{\bar\alpha_{t-1}} \underbrace{\left(\frac{\boldsymbol{x}_t-\sqrt{1-\bar\alpha_t} \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}{\sqrt{\bar\alpha_t}}\right)}_{\text {" predicted } \boldsymbol{x}_0 \text { " }}+\underbrace{\sqrt{1-\bar\alpha_{t-1}-\sigma_t^2} \cdot \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}_{\text {"direction pointing to } \boldsymbol{x}_t \text { " }}+\underbrace{\sigma_t \epsilon_t}_{\text {random noise }} \\&= \sqrt \frac{\bar\alpha_{t-1}}{\bar\alpha_t} x_t-\sqrt \frac{\bar\alpha_{t-1}}{\bar\alpha_t} \sqrt {1-\bar\alpha_t} \epsilon_\theta^{(t)} + \frac{1-\bar\alpha_{t-1}}{\sqrt{1-\bar\alpha_t}}\sqrt{\alpha_t} \epsilon_\theta^{(t)} + \sigma_t \epsilon_t \\&=\frac 1{\sqrt\alpha_t}x_t - \frac 1{\sqrt\alpha_t \sqrt{1-\bar\alpha_t}}\left(1-\bar\alpha_t+(1-\bar\alpha_{t-1})\alpha_t \right)\epsilon_\theta^{(t)} + \sigma_t \epsilon_t\\ &=\frac 1{\sqrt\alpha_t}\left(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}} \epsilon_\theta^{(t)} \right)+ \sigma_t \epsilon_t\\ &=\frac 1{\sqrt\alpha_t}\left(x_t - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}} \epsilon_\theta^{(t)} \right)+ \sigma_t \epsilon_t \end{aligned} \tag 9

因此，根据推导， $\eta=1$ 时候的 Forward Processes 等价于 DDPM，我们将在 notebook 后半部分，通过代码的方式验证当 $\eta=1$ DDIM 的结果与 DDPM 基本相同。

探索与思考

接下来将根据飞桨开源的 PaddleNLP/ppdiffusers，探索以下四个内容：

验证当 $\eta=1$ DDIM 的结果与 DDPM 基本相同。
DDIM 的加速采样过程
DDIM 采样的确定性
INTERPOLATION IN DETERMINISTIC GENERATIVE PROCESSES

读者可以在 Aistudio 上使用免费 GPU 体验以下的代码内容。链接：扩散模型探索：DDIM 笔记与思考open in new window

DDIM 与 DDPM 探索

验证当 $\eta=1$ DDIM 的结果与 DDPM 基本相同。

我们使用 DDPM 模型训练出来的 google/ddpm-celebahq-256 人像模型权重进行测试，根据上文的推导，当 $\eta=1$ 时，我们期望 DDIM 论文中的 Forward Process 能够得出与 DDPM 相同的采样结果。由于 DDIM 与 DDPM 训练过程相同，因此我们将使用 DDPMPipeline 加载模型权重 google/ddpm-celebahq-256 ，而后采用 DDIMScheduler() 进行图片采样，并将采样结果与 DDPMPipeline 原始输出对比。如下：

# DDPM 生成图片
pipe = DDPMPipeline.from_pretrained("google/ddpm-celebahq-256")

paddle.seed(33)
ddpm_output = pipe()  # 原始 ddpm 输出

# 我们采用 DDPM 的训练结果，通过 DDIM Scheduler 来进行采样。
pipe.scheduler = DDIMScheduler()

# 设置与 DDPM 相同的采样结果，令 DDIM 采样过程中的 eta = 1.
paddle.seed(33)
ddim_output = pipe(num_inference_steps=1000, eta=1)

imgs = [ddpm_output.images[0], ddim_output.images[0]]
titles = ["ddpm", "ddim"]
compare_imgs(imgs, titles)  # 该函数在 notebook_utils.py 声明

输出结果：

通过运行以上代码，我们可以看出 $\eta=1$ 时，默认配置下 DDPM 与 DDIM 采样结果有着明显的区别。但这并不意味着论文中的推导结论是错误的，差异可能源于以下两点：

计算机浮点数精度问题
Scheduler 采样过程中存在的 clip 操作导致偏差。

尝试去除 Clip 操作

Scheduler 采样过程中存在的 clip 操作导致偏差。Clip 操作对采样过程中生成的 x_0 预测结果进行了截断，尽管 DDPM, DDIM 均在预测完 $x_0$ 后进行了截断，但根据上文的推导公式，两者采样过程中 $x_0$ 权重的不同，可能导致了使用 clip 时，两者的采样结果有着明显区别。

将 clip 配置设置成 False 后， DDPM 与 DDIM( $\eta=1$ ) 的采样结果基本上相同了。如以下代码，我们尝试测试去除 clip 配置后的采样结果：

pipe = DDPMPipeline.from_pretrained("google/ddpm-celebahq-256")
pipe.progress_bar = lambda x:x  # uncomment to see progress bar

# 我们采用 DDPM 的训练结果，通过 DDIM Scheduler 来进行采样。
# print("Default setting for DDPM:\t",pipe.scheduler.config.clip_sample)  # True
pipe.scheduler.config.clip_sample = False
paddle.seed(33)
ddpm_output = pipe()

pipe.scheduler = DDIMScheduler()
# print("Default setting for DDIM:\t",pipe.scheduler.config.clip_sample)  # True
pipe.scheduler.config.clip_sample = False
paddle.seed(33)
ddim_output = pipe(num_inference_steps=1000, eta=1)

imgs = [ddpm_output.images[0], ddim_output.images[0]]
titles = ["DDPM no clip", "DDIM no clip"]
compare_imgs(imgs, titles)

可以验证得到 DDPM 与 DDIM 论文中提出的 $\eta=1$ 情况下的采样结果基本一致。

DDIM 加速采样

论文附录 C 有对这一部分进行详细阐述。DDIM 优化时与 DDPM 一样，对噪声进行拟合，但 DDIM 提出了通过一个更短的 Forward Processes 过程，通过减少采样的步数，来加快采样速度：

从原先的采样序列 $\{1,...,T\}$ 中选择一个子序列来生成图像。如原序列为 1 到 1000，抽取子序列可以是 1, 100, 200, ... 1000 （类似 arange(1, 1000, 100)）。抽取方式不固定。在生成时同样采用公式 $(1)$ ，其中的 timestep $t$ ，替换为子序列中的 timestep。其中的 $\bar\alpha_t$ 对应到训练时候的数值，比如采样 1, 100, 200, ... 1000 中的第二个样本，则使用训练时候采用的 $\bar\alpha_{100}$ （此处只能替换 alphas_cumprod $\bar\alpha$ ，不能直接替换 alpha 参数 $\alpha_t$ ）。

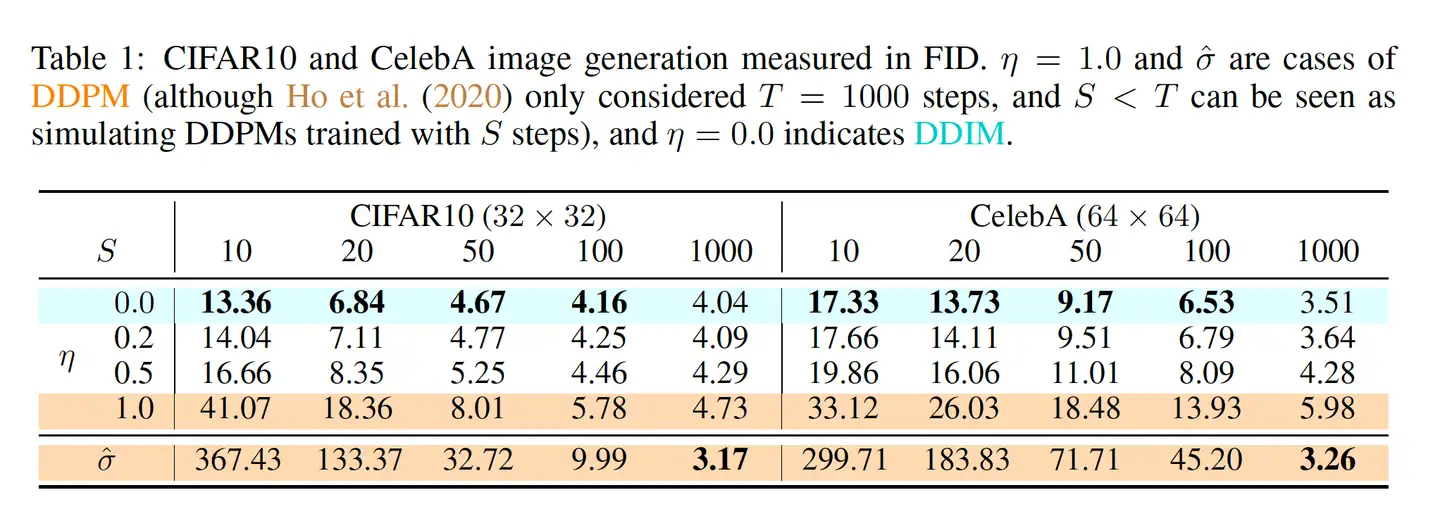
参考论文中的 Figure 3，在加速生成的情况下， $\eta$ 越小，生成的图片效果越好，同时 $\eta$ 的减小能够很大程度上弥补采样步数减少带来的生成质量下降问题。

我们尝试对论文中提到的上述方法进行复现：

pipe.progress_bar = lambda x:x  # cancel process bar
etas = [0, 0.4, 0.8]
steps = [10, 50, 100, 1000]
fig = plt.figure(figsize=(7, 7))
for i in range(len(etas)):
    for j in range(len(steps)):
        plt.subplot(len(etas), len(steps), j+i*len(steps) + 1)
        paddle.seed(77)
        sample1 = pipe(num_inference_steps=steps[j], eta=etas[i])
        plt.imshow(sample1.images[0])
        plt.axis("off")
        plt.title(f"eta {etas[i]}|step {steps[j]}")
plt.show()

通过论文中的示例说明，以及上述实现结果可以发现几点：

$\eta$ 越小，采样步数产生的 图片质量和风格差异 就越小。
$\eta$ 的减小能够很大程度上弥补采样步数减少带来的生成质量下降问题。

DDIM 采样的确定性

由于 DDIM 在生成过程中 $\eta=0$ ，因此采样过程中不涉及任何随机因素，最终生成图片将由一开始输入的图片噪声 $x_t$ 决定。我们采用不同的 random seed 进行采样：

paddle.seed(77)
x_t = paddle.randn((1, 3, 256, 256))
paddle.seed(8)
sample1 = pipe(num_inference_steps=50,eta=0,x_t=x_t)
paddle.seed(9)
sample2 = pipe(num_inference_steps=50,eta=0,x_t=x_t)
compare_imgs([sample1.images[0], sample2.images[0]], ["sample(seed 8)", "sample(seed 9)"])

图像重建

在 DDIM 论文中，其作者提出了可以将一张原始图片 $x_0$ 经过足够长的步数 $T$ 加噪为 $x_T$ ，而后通过 ODE 推导出来的采样方式，尽可能的还原原始图片。根据公式 $(5)$ （即论文中的公式 12），我们能够推理得到论文中的公式 $(13)$ :

\frac{\boldsymbol{x}_{t-\Delta t}}{\sqrt{\alpha_{t-\Delta t}}}=\frac{\boldsymbol{x}_t}{\sqrt{\alpha_t}}+\left(\sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}}-\sqrt{\frac{1-\alpha_t}{\alpha_t}}\right) \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right) \tag {10}

大致推导过程

\begin{aligned} \boldsymbol{x}_{t-1}&=\sqrt{\bar\alpha_{t-1}} \underbrace{\left(\frac{\boldsymbol{x}_t-\sqrt{1-\bar\alpha_t} \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}{\sqrt{\bar\alpha_t}}\right)}_{\text {" predicted } \boldsymbol{x}_0 \text { " }}+\underbrace{\sqrt{1-\bar\alpha_{t-1}-\sigma_t^2} \cdot \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}_{\text {"direction pointing to } \boldsymbol{x}_t \text { " }}+\underbrace{\sigma_t \epsilon_t}_{\text {random noise }} \\\frac{x_{t-1}}{\sqrt {\bar\alpha_{t-1}}}&= \frac {x_t}{\sqrt {\bar\alpha_t}} - \frac{\sqrt{1-\bar\alpha_t}}{\sqrt {\bar\alpha_t}}\epsilon_\theta^{(t)} + \frac{\sqrt {1-\bar\alpha_{t-1}}}{\sqrt {\bar\alpha_{t-1}}}\epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)\\ &\text {当 t 足够大时可以看做}\\\frac{\boldsymbol{x}_{t-\Delta t}}{\sqrt{\bar\alpha_{t-\Delta t}}} &=\frac {x_t}{\sqrt {\bar\alpha_t}} + \left(\sqrt{\frac{1-\bar\alpha_{t-\Delta t}}{\bar\alpha_{t-\Delta t}}}-\sqrt{\frac{1-\bar\alpha_t}{\bar\alpha_t}}\right) \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right) \end{aligned}

而后进行换元，令 $\sigma=(\sqrt{1-\bar\alpha}/\sqrt{\bar\alpha}), \bar x = x/\sqrt{\bar\alpha}$ ，带入得到：

\mathrm{d} \overline{\boldsymbol{x}}(t)=\epsilon_\theta^{(t)}\left(\frac{\overline{\boldsymbol{x}}(t)}{\sqrt{\sigma^2+1}}\right) \mathrm{d} \sigma(t)\tag{11}

于是，基于这个 ODE 结果，能通过 $\bar x({t}) + d\bar x(t)$ 计算得到 $\bar x(t+1)$ 与 $x_{t+1}$

根据 github - openai/improved-diffusionopen in new window，其实现根据 ODE 反向采样的方式为：直接根据公式 $(5)$ 进行变换，把 $t-1$ 换成 $t+1$ ：

\boldsymbol{x}_{t+1}=\sqrt{\bar\alpha_{t+1}} \underbrace{\left(\frac{\boldsymbol{x}_t-\sqrt{1-\bar\alpha_t} \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}{\sqrt{\bar\alpha_t}}\right)}_{\text {" predicted } \boldsymbol{x}_0 \text { " }}+\underbrace{\sqrt{1-\bar\alpha_{t+1}} \cdot \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}_{\text {"direction pointing to } \boldsymbol{x}_t \text { " }}+\underbrace{\sigma_t \epsilon_t}_{\text {random noise }}\tag{12}

而参考公式 $(11)$ 的推导过程， $(12)$ 可以看成下面这种形式：

\frac{\boldsymbol{x}_{t+\Delta t}}{\sqrt{\bar\alpha_{t+\Delta t}}} =\frac {x_t}{\sqrt {\bar\alpha_t}} + \left(\sqrt{\frac{1-\bar\alpha_{t+\Delta t}}{\bar\alpha_{t+\Delta t}}}-\sqrt{\frac{1-\bar\alpha_t}{\bar\alpha_t}}\right) \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)\tag {13}

以下我们尝试对自定义的输入图片进行反向采样（reverse sampling）和原图恢复，我们导入本地图片：

根据公式 12 编写反向采样过程。ppdiffusers 中不存在 reverse_sample 方案，因此我们根据本文中的公式 $(12)$ 来实现一下 reverse_sample 过程，具体为：

def reverse_sample(self, model_output, x, t, prev_timestep):
        """
        Sample x_{t+1} from the model and x_t using DDIM reverse ODE.
        """

        alpha_bar_t_next = self.alphas_cumprod[t]
        alpha_bar_t = self.alphas_cumprod[prev_timestep] if prev_timestep >= 0 else self.final_alpha_cumprod

        inter = (
                        ((1-alpha_bar_t_next)/alpha_bar_t_next)** (0.5)- \
                        ((1-alpha_bar_t)/alpha_bar_t)** (0.5)
                    )
        x_t_next = alpha_bar_t_next** (0.5) * (x/ (alpha_bar_t ** (0.5)) + \
                    (
                    model_output * inter
                    )
                )

        return x_t_next

而后进行不断的迭代采样与图片重建（具体的方式可以查看扩散模型探索：DDIM 笔记与思考open in new window）。以下右图为根据原图进行反向 ODE 加噪后的结果，可以看出加噪后和电视没信号画面相当。以下左图为根据噪声图片采样得来的结果，基本上采样的结果还原了 90%以上原图的细节，不过还有如右上角部分的一些颜色没有被还原。

潜在的风格融合方式

通过两个能够生成不同图片的噪声 $z_1, z_2$ ，进行 spherical linear interpolation 球面线性插值。而后作为 $x_T$ 生成具有两张画面共同特点的图片。有点类似风格融合的效果。参考 linkopen in new window。首先我们选取两个不同的图片进行融合：

paddle.seed(77)
pipe.scheduler.config.clip_sample = False

z_0 = paddle.randn((1, 3, 256, 256))
sample1 = pipe(num_inference_steps=50,eta=0,x_t=z_0)
paddle.seed(2707)
z_1 = paddle.randn((1, 3, 256, 256))
sample2 = pipe(num_inference_steps=50,eta=0,x_t=z_1)
compare_imgs([sample1.images[0], sample2.images[0]], ["sample from z_0", "sample from z_1"])

输出结果：

以上选择 seed 为 77 和 2707 的噪声进行采样，他们的采样结果分别展示在上方。

以下参考 ermongroup/ddim/blob/main/runners/diffusion.pyopen in new window ，对噪声进行插值，方式大致为：

x_t = \frac {\sin\left((1-\alpha)\theta\right)}{\sin(\theta)}z_0 + \frac{sin(\alpha\theta)}{\sin(\theta)}z_1,\\where\ \theta=\arccos\left(\frac{\sum z_1z_0}{||z_1|·||z_0||}\right)

def slerp(z1, z2, alpha):
    theta = torch.acos(torch.sum(z1 * z2) / (torch.norm(z1) * torch.norm(z2)))
    return (
        torch.sin((1 - alpha) * theta) / torch.sin(theta) * z1
        + torch.sin(alpha * theta) / torch.sin(theta) * z2
    )