VDM学习笔记

摘要

• 在基本理解着证据下界和VAE后，学习VDM，主要是想自己理解顺畅整个模型的思路和推导过程（done）。
• 内容组织：
• 首先从宏观感受VDM的模型架构，并与HVAE进行比较，基本理解；
• 然后讲解自己理解的整个模型建模过程和原因(《事后诸葛》，为了自己理解)；
• 指出VDM的三个重要等价解释，着重Score-Based Model进行比较（等价解释3），利于理解模型的可控建模（Diffusion-LM）
• 最后为可控性的加入和VDM的问题
• 训练和推理的算法

（1）宏观感受

1.带限制条件的HVAE

1. latent space和data space的维度是一样的
1. 数学表示不再使用 、𝑥、𝑧 ，统一使用 𝑥0:𝑇 表示，非0部分为latent space
2. 编码的过程是非学习的，是预定义的线性高斯模型（不断➕高斯噪声）
1. 𝑞(𝑥𝑡|𝑥𝑡−1)=𝑁(𝑥𝑡;𝛼𝑡𝑥𝑡−1,(1−𝛼𝑡)𝐼)
2. 其中 𝛼𝑡 是一个变化系数，一般随t变小（可以固定方法或者学习的方式），使得 𝑝(𝑥𝑇) 为标准高斯分布
3. 编码过程汇总的高斯参数变化使得最终的laten space（ ）𝑥𝑇） 是标准高斯分布

• 联合分布为：

联合分布（连续的马尔可夫性可得）

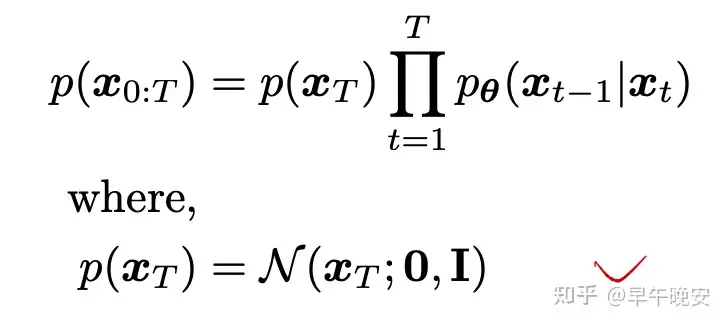
2.宏观角度

下方为扩散，上方为生成过程

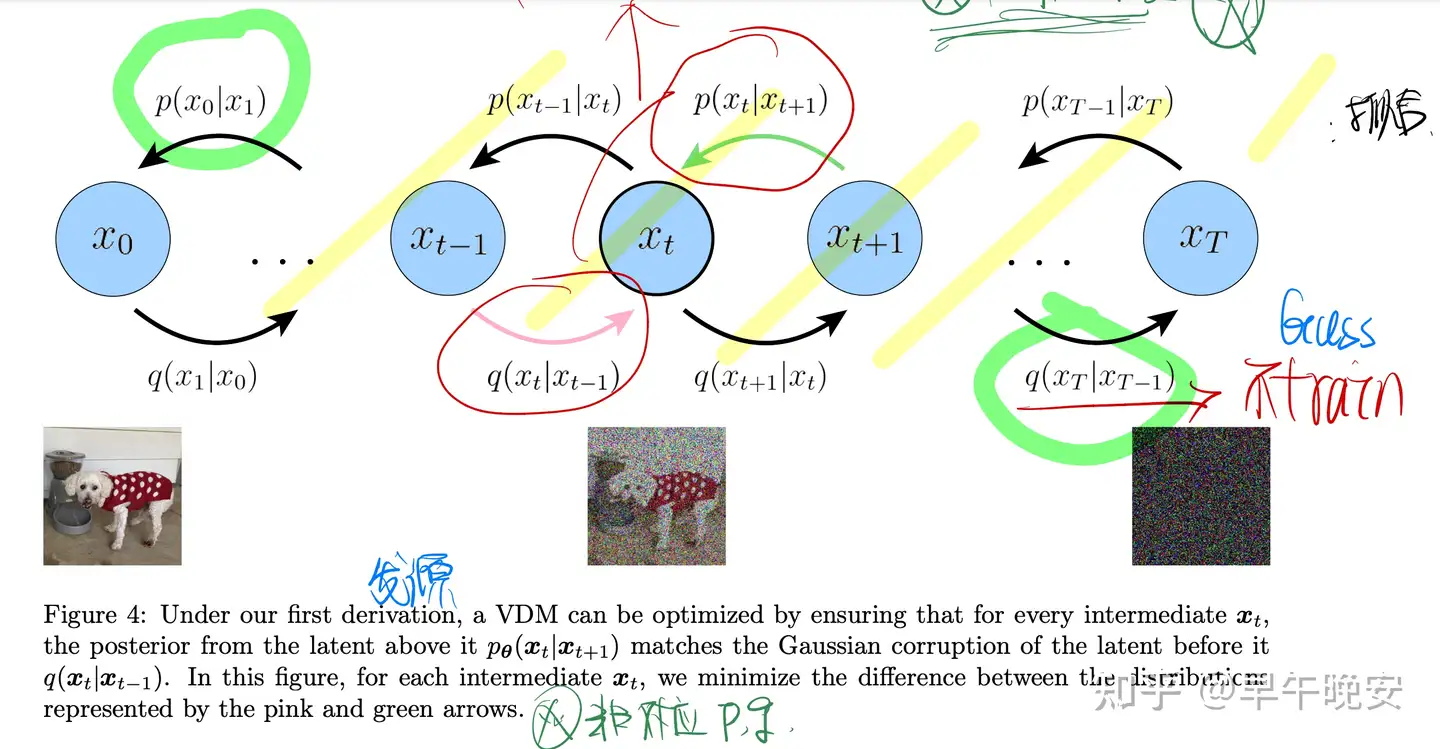
• 扩散过程：不断往原图中加高斯噪声，直到最终完全成为高斯噪声
• 此过程是预先确定的（系数 𝛼𝑡 也是以一种固定的方式或者学习的方式得到）不用学习和训练
• 是确定的均值方差的高斯模型，和VAE需要变分推断不同
• 生成过程（逆扩散）：
• 扩散过程是确定的，因此生成过程 𝑝𝜃(𝑥𝑡−1|𝑥𝑡) 是需要研究的点
• 和VAE一样，生成过程需要最大化证据 log⁡𝑝(𝑥) 也就是需要最大化证据下界 𝐸𝐿𝐵𝑂

（2）建模过程

1.最大化证据下界ELBO

KL散度的“提”出来的过程

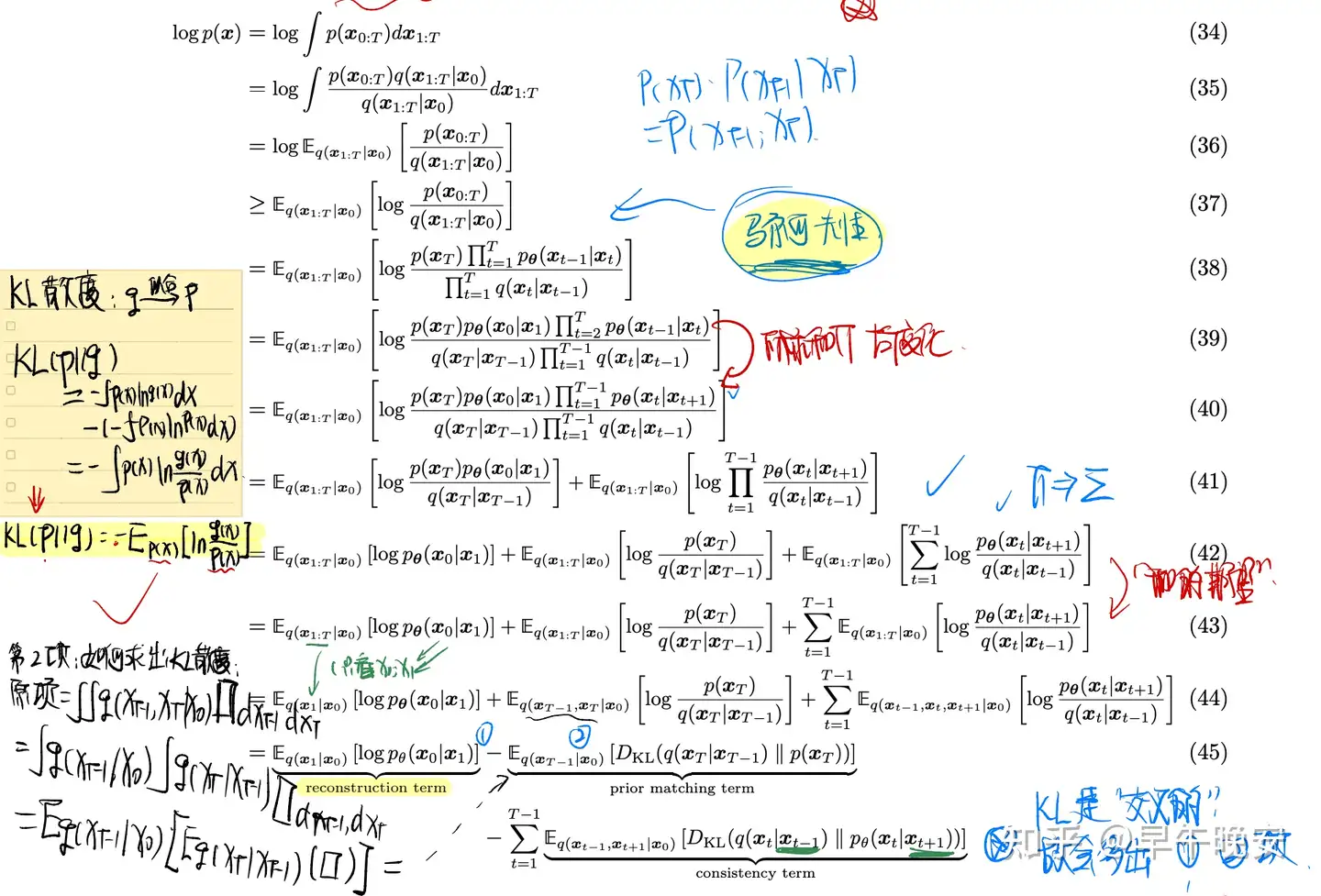
1. 用到的点：

• 杰森不等式：过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方
• 是凸函数Φ(𝐸(𝑥))≤𝐸(Φ(𝑥))Φ是凸函数
• 马尔科夫性
• KL散度(相对熵) ：
• 用分布拟合分布则到的散度为用分布𝑄拟合分布𝑃,则𝑃到𝑄的𝐾𝐿散度为𝐷𝐾𝐿(𝑃||𝑄)=−∫𝑝(𝑥)ln⁡𝑝(𝑥)𝑞(𝑥)𝑑𝑥=−𝐸𝑝(𝑥)ln⁡𝑝(𝑥)𝑞(𝑥)
• (43)到(44)的推导-下标是咋改变的（第一项为例）

• (44)到(45)的推导：

(44)到(45)的推导

2.三个项的解释：

• reconstruction term：和VAE一样的重构部分，训练和VAE一样，通过蒙特卡洛估计（图绿色圈）
• prior matching term：最小化最后一层和高斯分布的差距，不用学习，因为特点3
• consistency term：重点：目的：使得在 𝑥𝑡 在扩散和生成过程连贯一致

3. 其他：

• （⚠️注意图中扩散部分和生成过程的对应关系）
• 故最大化证据下界ELBO,最主要就是处理consistency term部分，也是优化主要代价所在——需要在每一步进行最小化，reconstruction term也会一起优化了
• 同时：以上用到了很多期望，实际上使用蒙特卡洛算法进行估计

2.最小化consistency term

• 观察consistency term：

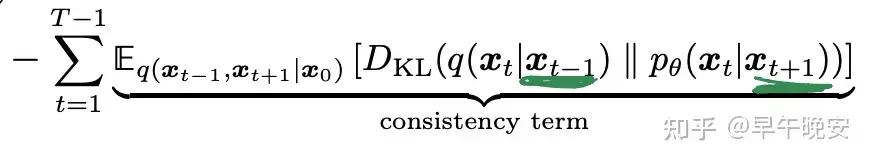
• 优化问题：
• 由于是求两个随机变量 、𝑥𝑡、𝑥𝑡−1 的期望，因此求出来的结果肯定是不佳的，方差会很大
• 其次，整个过程需要在不同的时间步进行优化，代价比较大
• 目标：
• 使得依赖于同一个随机变量，
• 并且可以在一开始就求出 𝑞(𝑥𝑡|𝑥𝑡−1) ，如 𝑓(𝑥0)
• 方法推导：

1. 马尔科夫引入x_0+贝叶斯公式修改:
1. 𝑞(𝑥𝑡|𝑥𝑡−1)=𝑞(𝑥𝑡|𝑥𝑡−1,𝑥0)=𝑞(𝑥𝑡−1|𝑥𝑡,𝑥0)𝑞(𝑥𝑡|𝑥0)𝑞(𝑥𝑡−1|𝑥0)
2. 重新带入最大化 𝐸𝐿𝐵𝑂 ：

下面接着

接着上面

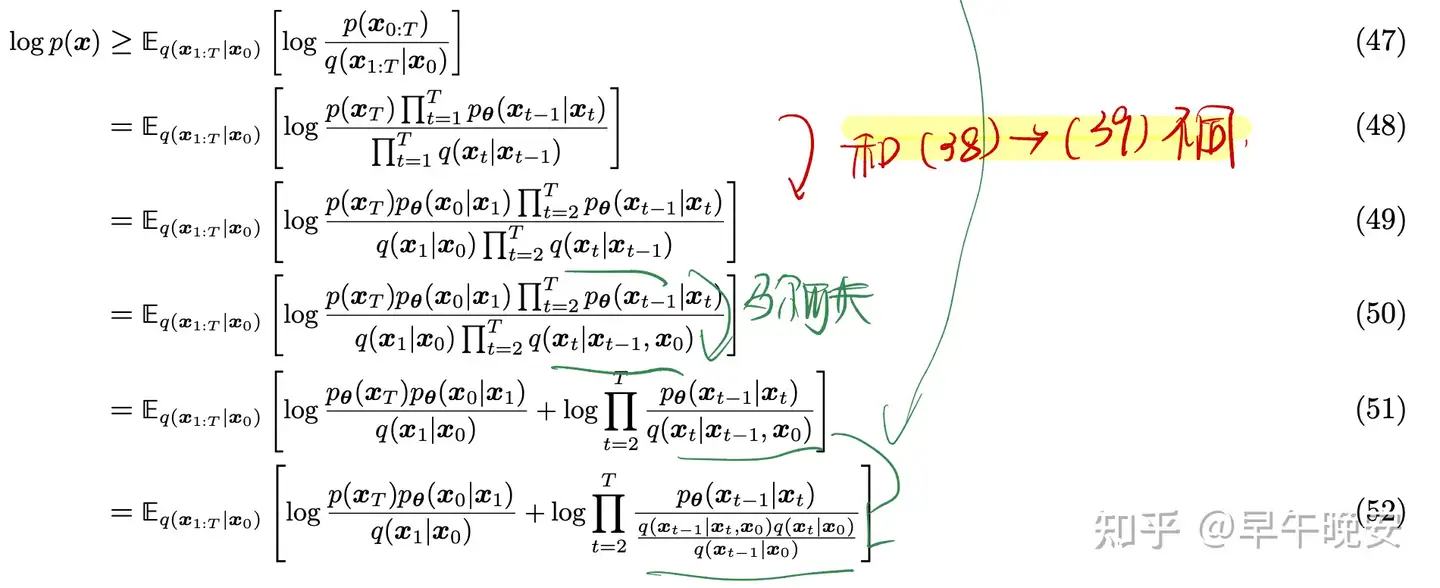
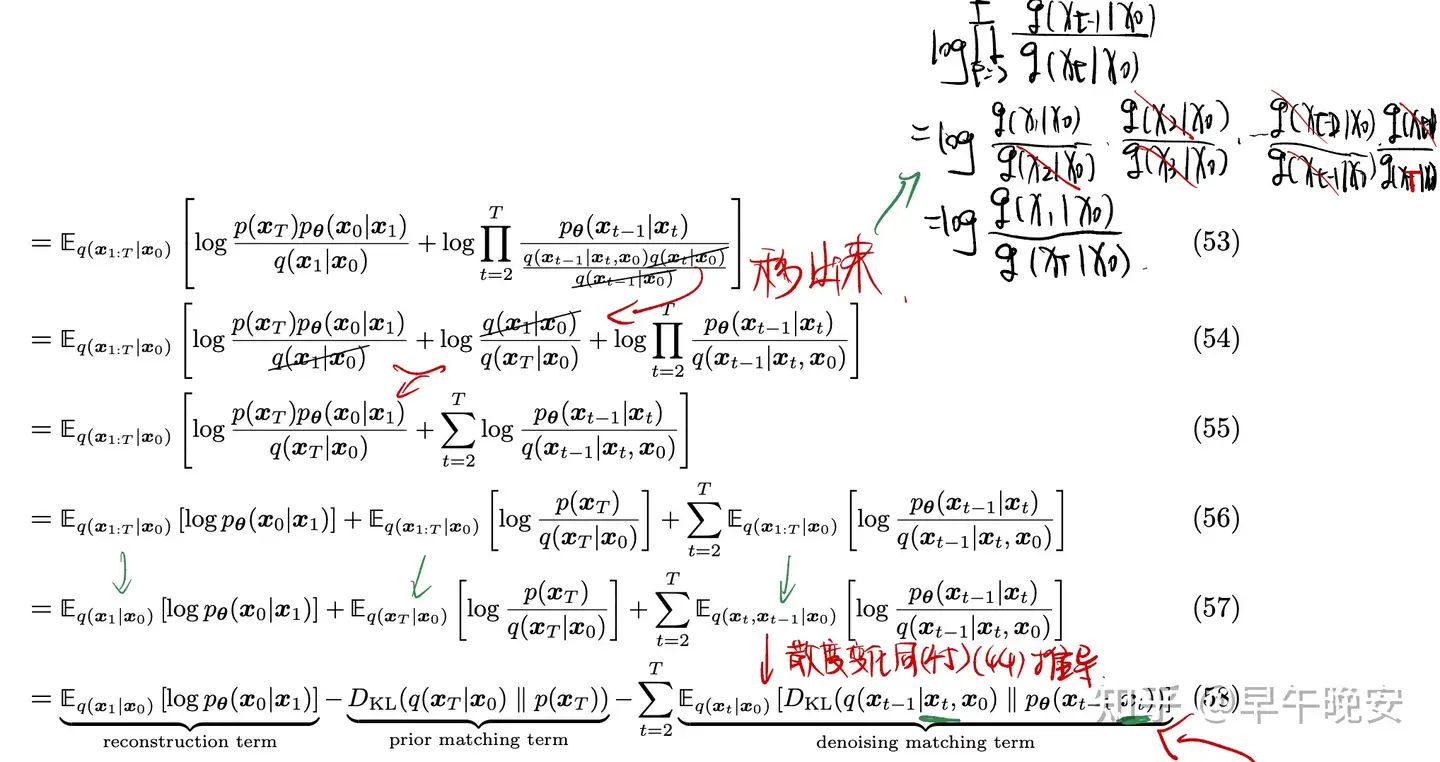
• 推导解释：
• (53)-(54)如图：先通过log✖️转➕，对移除项进行展开处理得到
• (57)-(58)同之前的KL推导
• 实际上当T=1时，和之前VAE的目标是一样的

拟合过程(粉色、绿色、黑色)

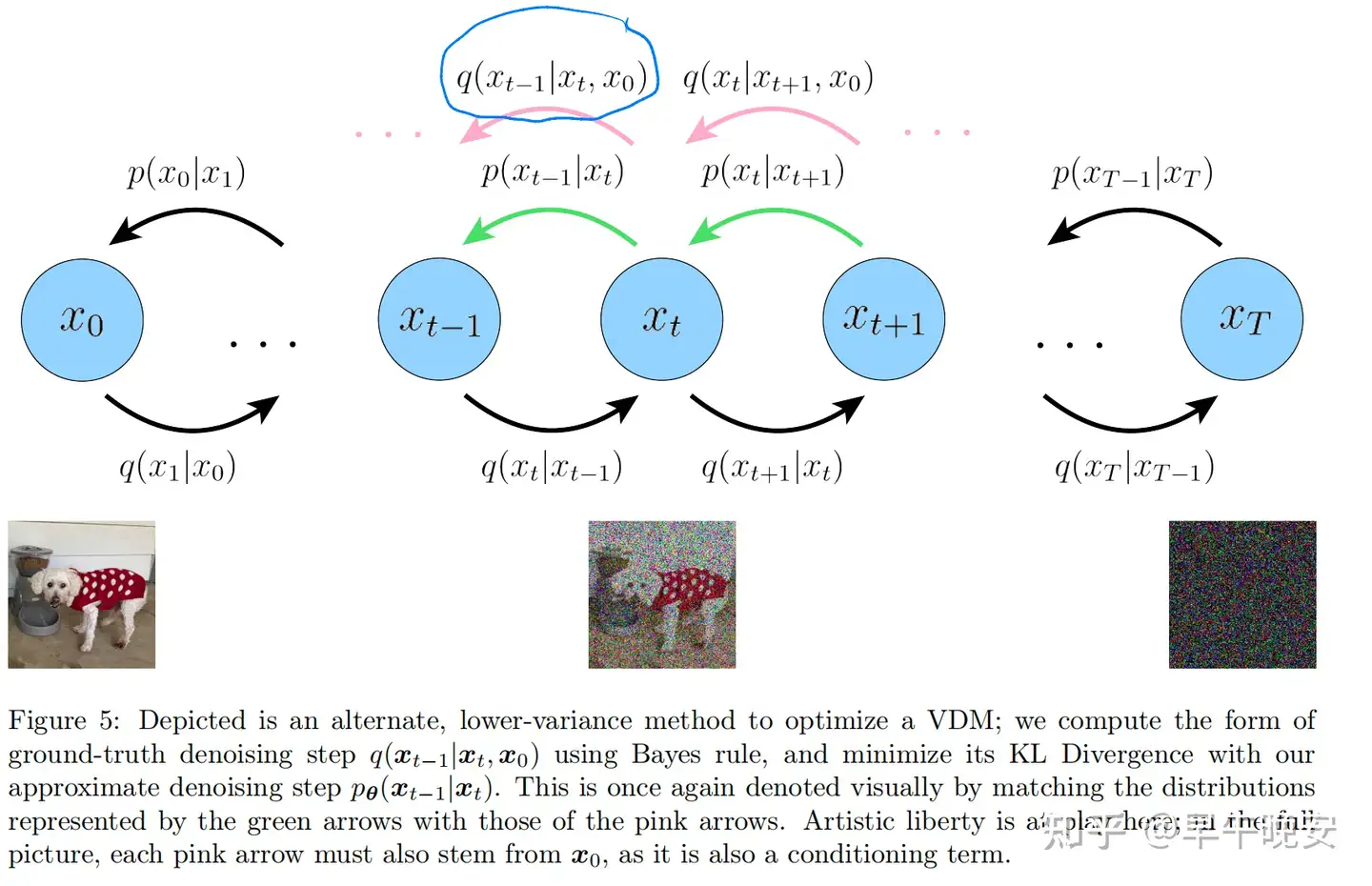
• 重要的三部分：
• denoising matching term：关键
• 求的期望由一个随机变量确定，解决了第一个问题
• 最小化KL就是用 𝑝𝜃(𝑥𝑡−1|𝑥𝑡) 拟合一个去燥，ground truth是 𝑞(𝑥𝑡−1|𝑥𝑡,𝑥0)
  后者可理解为：给定原图目标 𝑥0 ，咋从t步走到t-1。

3.拟合去噪过程（生成过程）

• 关键就是:（如上图）

1. 求 𝑞(𝑥𝑡−1|𝑥𝑡,𝑥0)
2. 拟合之

 

1. 在VAE中，优化生成过程是需要同时考虑推断过程的，但是在VDM中，我们知道了扩散（推断）是线性高斯分布模型，故，我们可以利用这个性质来进行求解
2. 要利用 𝑞(𝑥𝑡|𝑥𝑡−1) 高斯分布的性质，故需要对 𝑞(𝑥𝑡−1|𝑥0,𝑥𝑡) 进行构造：

• 贝叶斯+马尔可夫+再参数化+高斯分布的性质
• 再参数化：函数的参数1为参数2的函数，故函数为参数2函数的函数
• 如下公式，需要处理分子两项，前者通过马尔科夫进行，后者通过再参数化求解

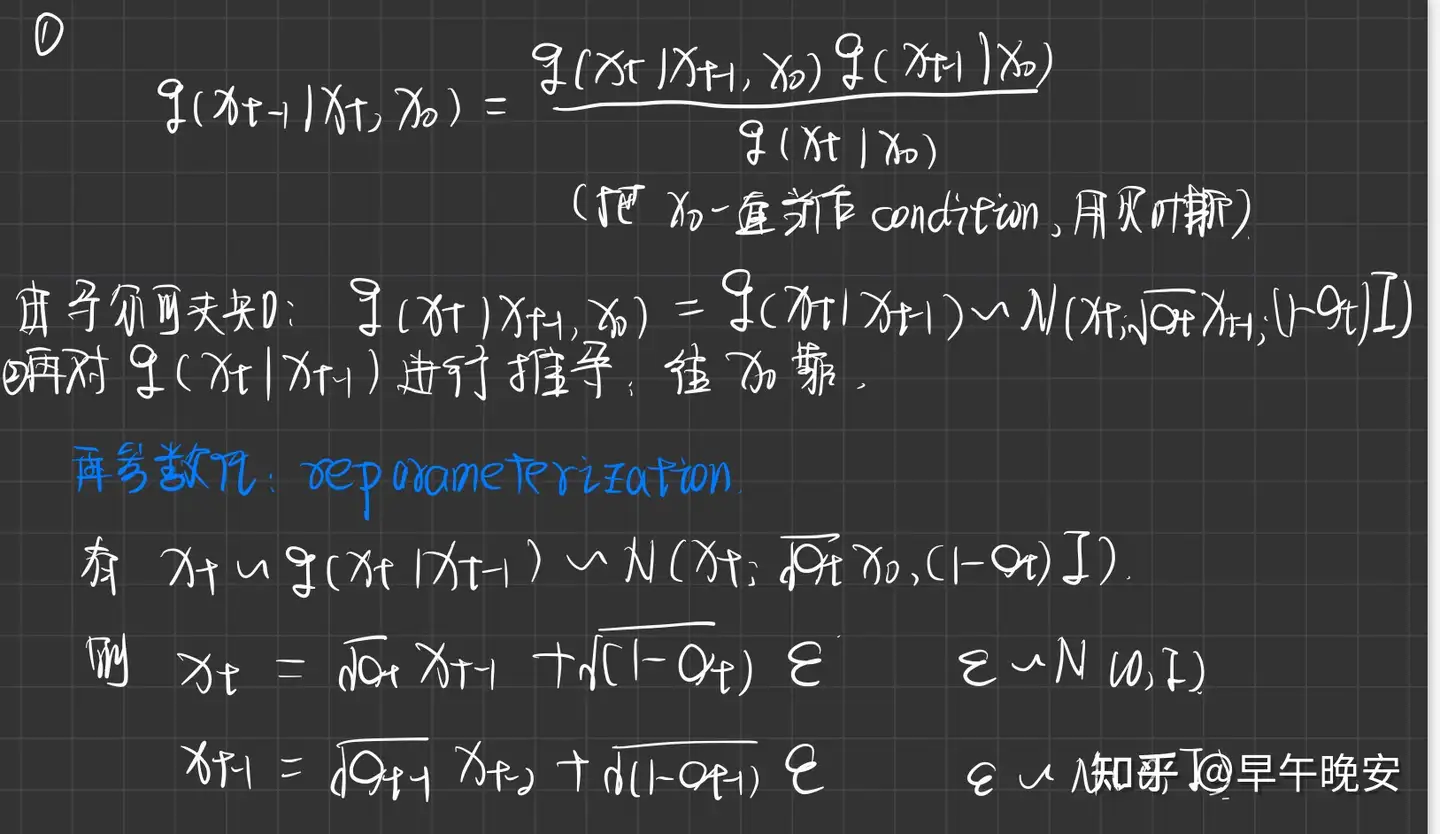
• 1.故迭代带入得到 𝑥𝑡 服从 𝑞(𝑥𝑡|𝑥0) (相当于一连串的再参数化)

• 𝜖 的处理：
  两个高斯分布加和的性质：均值相加，方差相加
• 这样，扩散时的 𝑥𝑡 系数可以在之前就求出来，基于 𝑥0 也可以求的了
• 2.带入原式继续让其向 𝑥0 靠:

(74)(75)推导拆开后，相对于 𝑥𝑡−1 ,有一个与之无关的常量 𝑐(𝑥𝑡,𝑥0) ，后次常量在(84)时用于构造方差，构造高斯分布的形式。

• 第一步结果出来了：
• 结论： 𝑞(𝑥𝑡−1|𝑥𝑡,𝑥0) ，求出来了，和 𝑥𝑇,𝑥0 相关的高斯分布
• 其中均值：方差：均值：𝜇𝑞=(𝑥𝑡,𝑥0)方差：∑𝑞(𝑡)=𝑓(𝛼)
• 𝛼 是固定的计算方式，或者是学习得到的

4.用 𝑝𝜃(𝑥𝑡−1|𝑥𝑡) 拟合

• 我们知道了ground truth是高斯分布的，那么为了拟合更好，我们可假设 𝑝𝜃(𝑥𝑡−1|𝑥𝑡) 也是高斯分布，且 𝛼 是每一步都明确的，因此p和q，去燥和扩散的两个过程的方差都是一样的均为 ∑𝑞(𝑡) ，故需要建模均值 𝜇𝜃

1. 建模均值 𝜇𝜃 :

• 均值 𝜇𝜃 肯定是 𝑥𝑡 的函数，其和 𝑥0 无关
• 有：两个高斯分布的KL散度计算为：
• 故，我们拟合去燥和扩散（也就是最小化KL散度）得到：

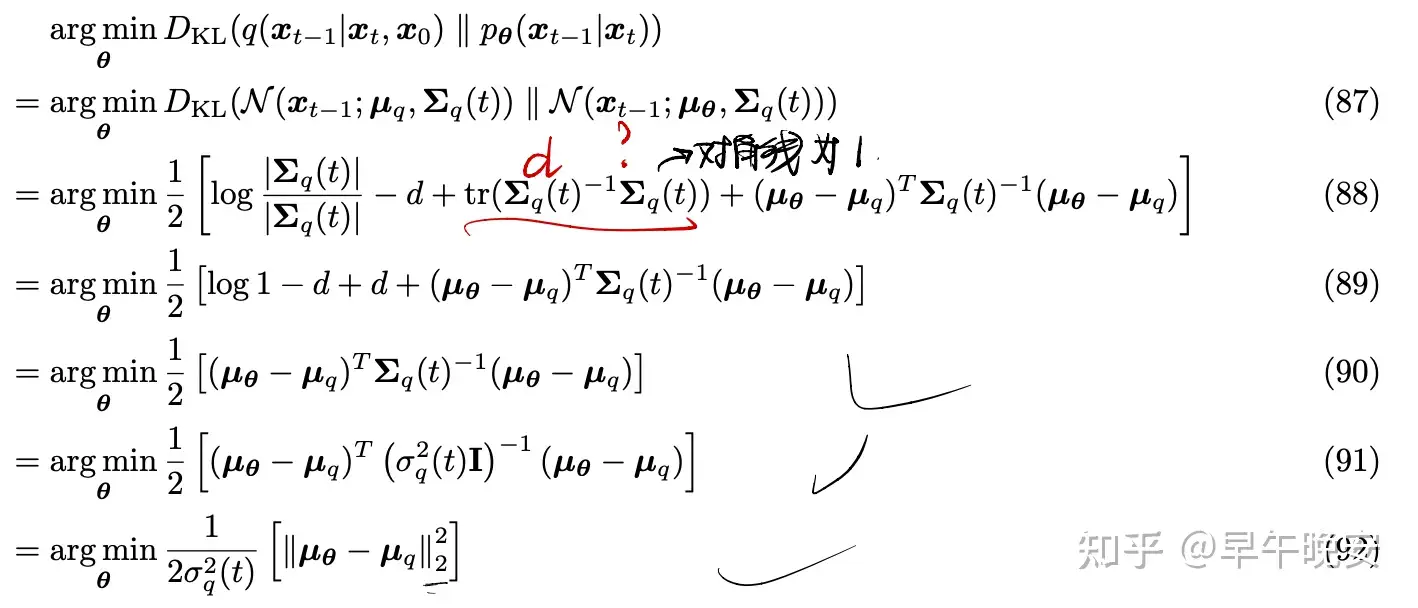
• 最小化KL散度就是让去燥和扩散的均值尽量拟合，我们知道：

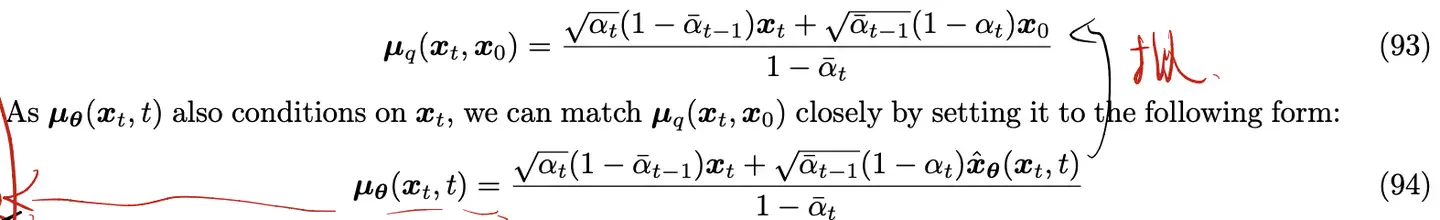
• 其中： 𝑥^𝜃(𝑥𝑡,𝑡) 是一个神经网络，用于拟合 𝑥0 ——（U-Net、Transformer）
• 再代入公式(92)得到：

相当于：在t步，预测原始数据x_0s

两个高斯分布的KL散度计算

1. 结论：
1. 优化扩散模型其实就是学习一个神经网络（预测函数），在每一步t，利用𝑥𝑡，t对原图𝑥0进行预测

5.总体目标：

最终的整体学习目标

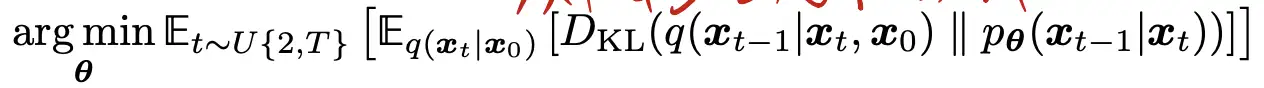
（3）重要等价解释

• VDM学习目标的三个等价解释：学习一个网络（U-net 或 Transformer）：

1. 用任意一个加噪后的样本预测原始样本
1. arg⁡min𝜃||𝑥^𝜃(𝑥𝑡,𝑡)−𝑥0||22
2. 用任意一个加噪后的样本预测所加的噪声
1. arg⁡min𝜃||𝜖0−𝜖^𝜃(𝑥𝑡,𝑡)||22
1. 解释：
1. 我们知道了 𝑞(𝑥𝑡|𝑥0) 的分布是如何的，因此可以写出:
1. 𝑥0=𝑥𝑡−1−𝛼¯𝑡𝜖0𝛼¯𝑡
2. 代入 𝜇𝑞(𝑥𝑡,𝑥0) 化简，同理设计 𝜇𝜃(𝑥𝑡,𝑡)

上方为\mu_q化简

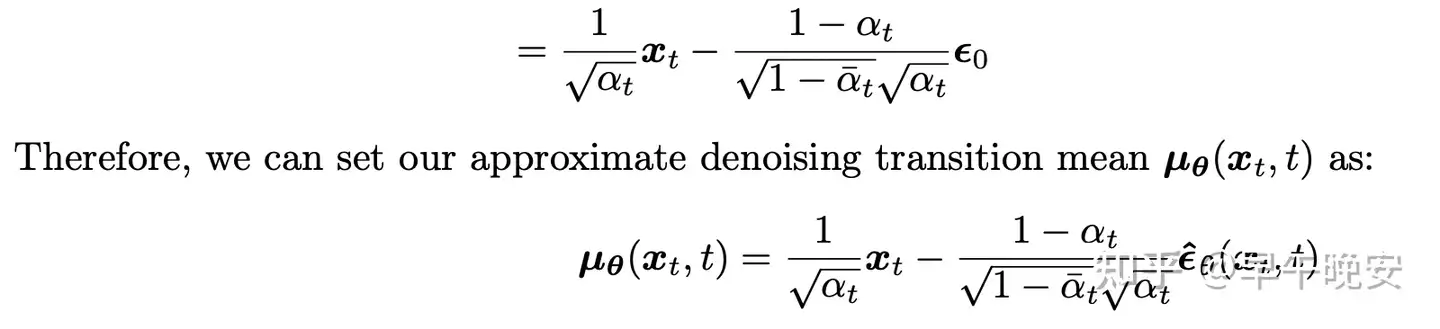
3.对任意一个噪声层次上对一个加噪图像进行打分（设计Score-Based Model的理解）

arg⁡min𝜃||𝑠𝜃(𝑥𝑡,𝑡)−∇𝑥𝑡log⁡𝑝(𝑥𝑡)||22

• 解释：
• Tweedie’s Formula:

Tweedie’s Formula

• 同样，将 𝑥0 代入化简，得到:

接着

• 问题：
• 打分函数有什么意义？

4.Score-besed Model

1. 能量模型(energybased models)

• 任意一个概率分布，可以写为：
• 𝑝𝜃(𝑥)=1𝑍𝜃exp⁡(−𝑓𝜃(𝑥))
• 𝑓𝜃(𝑥) 是一个能量函数，用神经网络建模
• 优化目标还是最大化证据 log⁡𝑝𝜃(𝑥) ，对其求梯度，用梯度进行优化（自己理解的），梯度就是一个打分函数
• 并且直接求是不容易的，因此会使用ANN学习一个 𝑠𝜃(𝑥𝑡,𝑥) 对梯度进行估计：

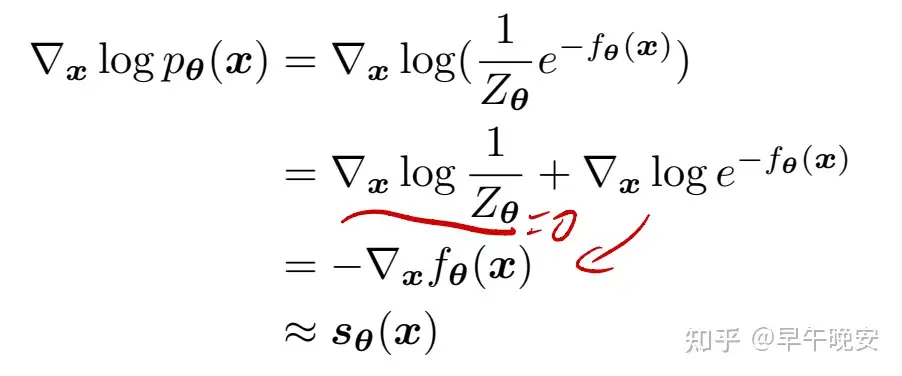
• 优化目标就是：

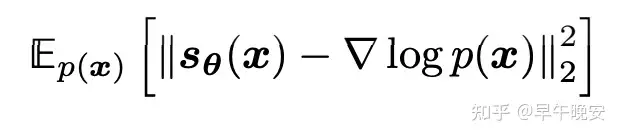
2. score function 的意义!

• 梯度的意义 ∇𝑥𝑡log⁡𝑝(𝑥𝑡) :
• 指明最大化证据（似然估计）的方向
• 因此，score function就是学习这样一个函数，能够去描述整个数据集，在进行数据生成的时候，在数据空间中的任意一点，我们可以用这个函数去指导生成过程，迭代地朝着我们想要的目标靠近（右图）

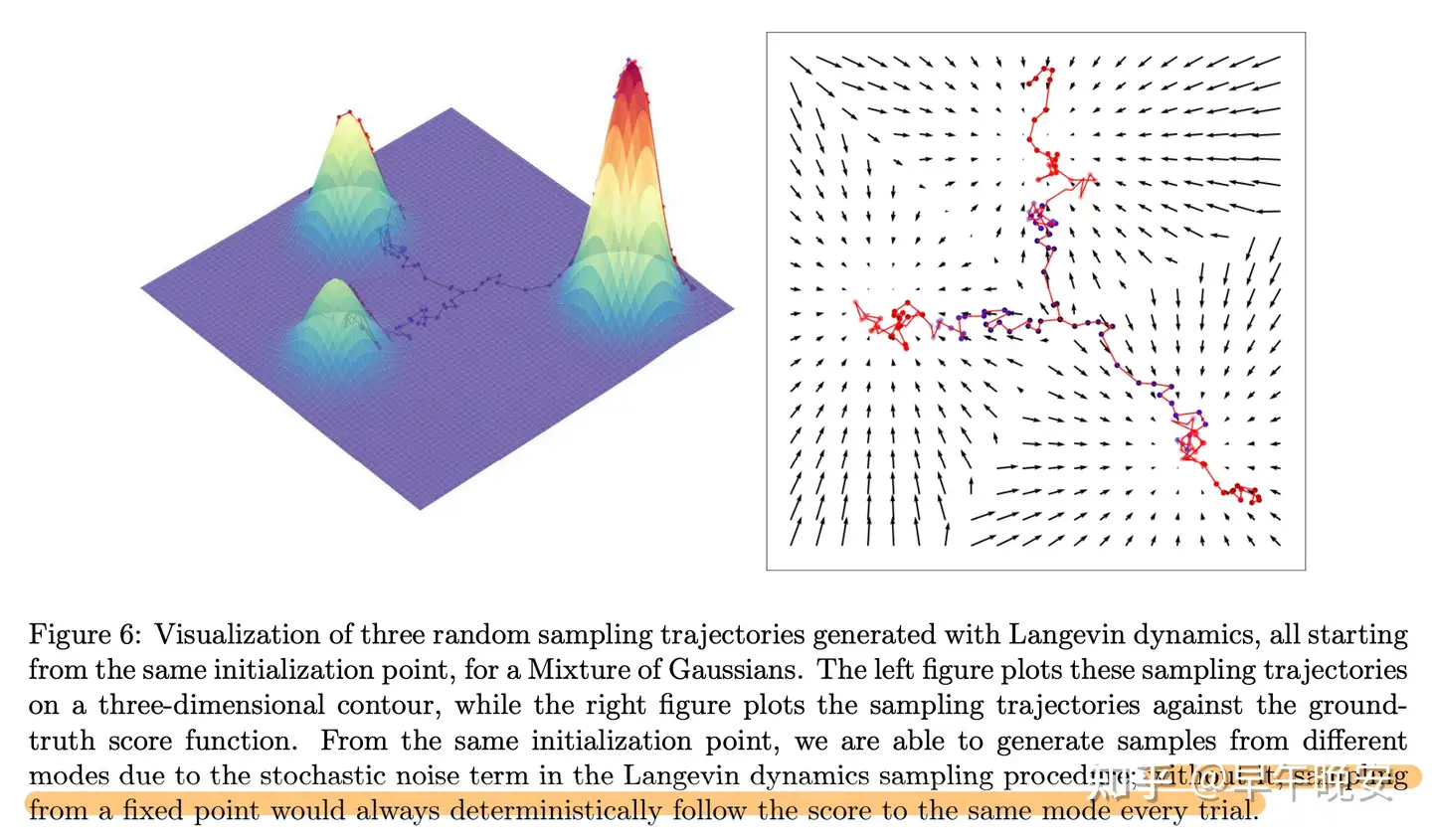
3.Langevin dynamics（朗之万方程）（迭代过程）

• 朗之万方程，用于描述自由度的子集的时间演化的随机微分方程，
• 描述布朗运动（或者就热力学里状态逐渐稳定的过程（好像是））

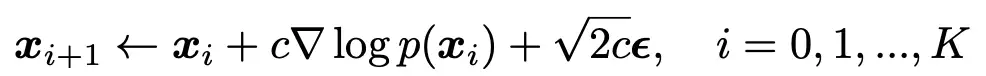
• 解释：
• 𝑥0 是一个先验分布的采样，
• 𝜖 是一个标准高斯分布噪声：
• 可以让生成的数据不会直接坍塌到目标mode，而是在周围产生浮动保证多样性
• 同时，由于打分函数是固定的，那么指导方向路径就是一定的，加入噪声有利于避免这样一个确定的轨迹进行（如图，即使从同一个点出发，由于有了高斯噪声，也可以到达三个不同的极值处）

4.优化方法：

• 优化目标：

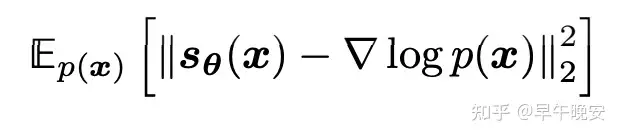
• 优化方法：score matching
• 可以不用知道ground truth同时利用SGD进行求解
• 问题之一：
• 如： 𝑝(𝑥)=𝑐1𝑝1(𝑥)+𝑐2𝑝2(𝑥)
• 由于取对数，这样的混合分布就没办法求的参数（取对数，求倒后为0，分布的权重就一样了）
• 问题就是：如Figure 6(上图)，学习的打分函数对每个部分的权重都是一样的，这样即使右下方更高，权重大，但是生成过程也是等概率走向各个极值（mode，不同的数据目标）
• 解决方法：
• 添加方差逐渐变大的高斯噪声
• 总体优化目标：

• 解释：
• 𝜆(𝑡) 是一个权重函数
• 朗之万方程迭代生成过程中，随机从先验分布中采样然后迭代，其所添加的高斯分布方差逐渐变大，(160)添加的噪声就会逐渐变小，最后就趋近于真实的分布 𝑝(𝑥) （这点和VDM的生成类似）
• 总结：啥是score-based model：
  Collectively, learning to represent a distribution as a score function and using it to generate samples through Markov Chain Monte Carlo techniques, such as Langevin dynamics, is known as Score-based Generative Modeling

5.和VDM 联系：

• 总体优化目标就和VDM的很像
• 生成过程也类似

6. 总结：

• 主要是知道打分函数的作用
  ：用来描述数据分布，指导采样后的数据在生成过程中，往哪个方向生成（最大化证据 log⁡𝑝(𝑥) ）

（4）VDM的训练和推理

DDP训练与推理

（5）条件概率建模——可控性的添加

• 可控生成，宏观来看就是建模条件概率，生成给定条件概率下，生成模型（和可解释性有点点不同）

1. 条件概率建模： 𝑝(𝑥|𝑦)

• 联合概率分布为：

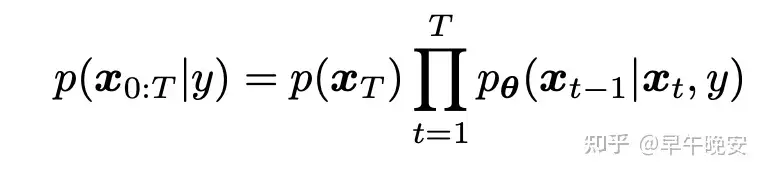
• 因此，之前VDM的关键：ANN拟合的三个对象就变为：
• arg⁡min𝜃||𝑥^𝜃(𝑥𝑡,𝑡,𝑦)−𝑥0||22arg⁡min𝜃||𝜖0−𝜖^𝜃(𝑥𝑡,𝑡,𝑦)||22arg⁡min𝜃||𝑠𝜃(𝑥𝑡,𝑡,𝑦)−∇𝑥𝑡log⁡𝑝(𝑥𝑡|𝑦)||22

2. 用打分函数建模

3. Classifier- Guidance

• 基于贝叶斯公式：

• 前者就是正常的非条件建模，后者为一个分类预测的梯度（使用Classifier）
• 【potential function】：评估当前数据 𝑥𝑡 和我们的条件 𝑦 的符合程度，用其他方式也可以
• 所学习的打分函数就是分类器梯度和非条件的打分函数和
• 打分函数

classifier-guidance score function

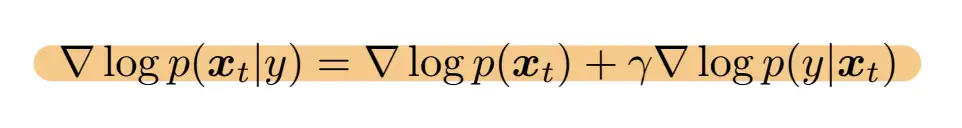
• 𝛾 是超参，指定关注条件的程度
• 训练方法：
• 分类器需要沿着整个 0:𝑇 进行训练
• 好处:
• 扩散模型可以是训练好的
• 即插即用

4. Classifier-Free Guidance

• 基本思想就是建模“两个”扩散模型，从头开始训：
• 分类器梯度进一步用贝叶斯修改

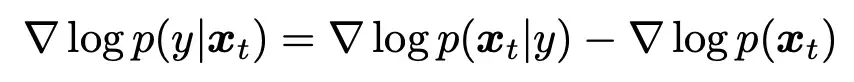
• 打分函数为：

• 𝛾 大于1时，可以减少模型忽略条件的概率

（6）VDM的问题

• 和人类的思维是不一样的（AI的角度）
• （AI是在机器上模拟人类的智能）
• （飞机并不是模拟小鸟，而是研究空气动力学）
• latent space的维度限制和数据维度相同，限制了学习有意义、压缩的隐空间
• 可解释性：VDM的编码是加噪声的过程，各个latent space只是加噪声的原图。VAE的encoder可以优化，有希望学习结构化、有意义的隐空间
• 文本和图像的噪声定义也应该不同
• 采样的代价比较大

---

笔记总结：

• 部分数学公式、score-based模型优化（score matching）没有深究，后续遇到问题或有空继续
• 基本目标达成，
• 后续任务：
• DDPM和improved的文章+代码阅读（代码进一步理解模型整个过程）
• 重点：NLP、Multimodal的相关文章阅读
• 感兴趣：可解释的Diffusion Models already have a Semantic Latent Space

参考文献