一篇deffusion的博客

[2021-09-19更新：强烈推荐Yang Song的这篇关于基于得分的生成建模的博文（几篇参考文献的主要作者）]。
[2022-08-27更新：添加了无分类器引导，GLIDE，unCLIP和Imagen。
[2022-08-31更新：添加了潜在扩散模型。
[2024-04-13更新：添加了渐进蒸馏，一致性模型，和模型架构部分。

到目前为止，我已经写了三种生成模型，GAN，VAE和基于流的模型。它们在生成高质量样本方面取得了巨大的成功，但每种模型都有其自身的局限性。由于对抗训练的性质，GAN模型的训练可能不稳定且生成的多样性较差。VAE依赖于代理损失函数。流模型必须使用专门的架构来构建可逆变换。

扩散模型受到非*衡热力学的启发。它们定义了一个马尔可夫链的扩散步骤，通过逐步向数据添加随机噪声，然后学习逆转扩散过程，从噪声中构造所需的数据样本。与VAE或流模型不同，扩散模型通过固定的程序进行学习，潜变量具有与原始数据相同的高维度。

图1. 各种生成模型的概述。

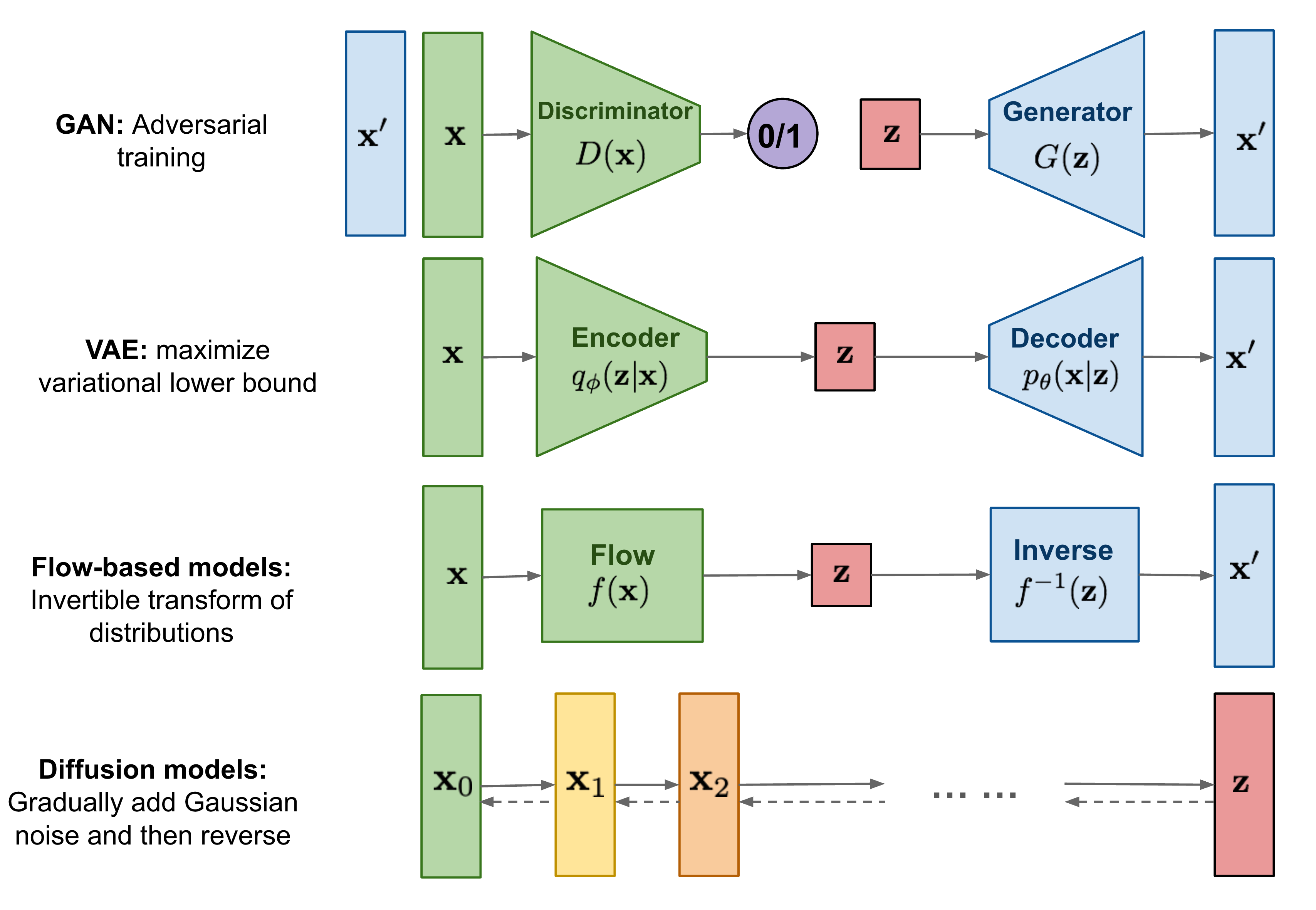
什么是扩散模型？

已经提出了几种基于扩散的生成模型，它们具有相似的基本思想，包括扩散概率模型(Sohl-Dickstein等，2015)、噪声条件得分网络(NCSN；Yang & Ermon，2019)和去噪扩散概率模型(DDPM；Ho等，2020)。

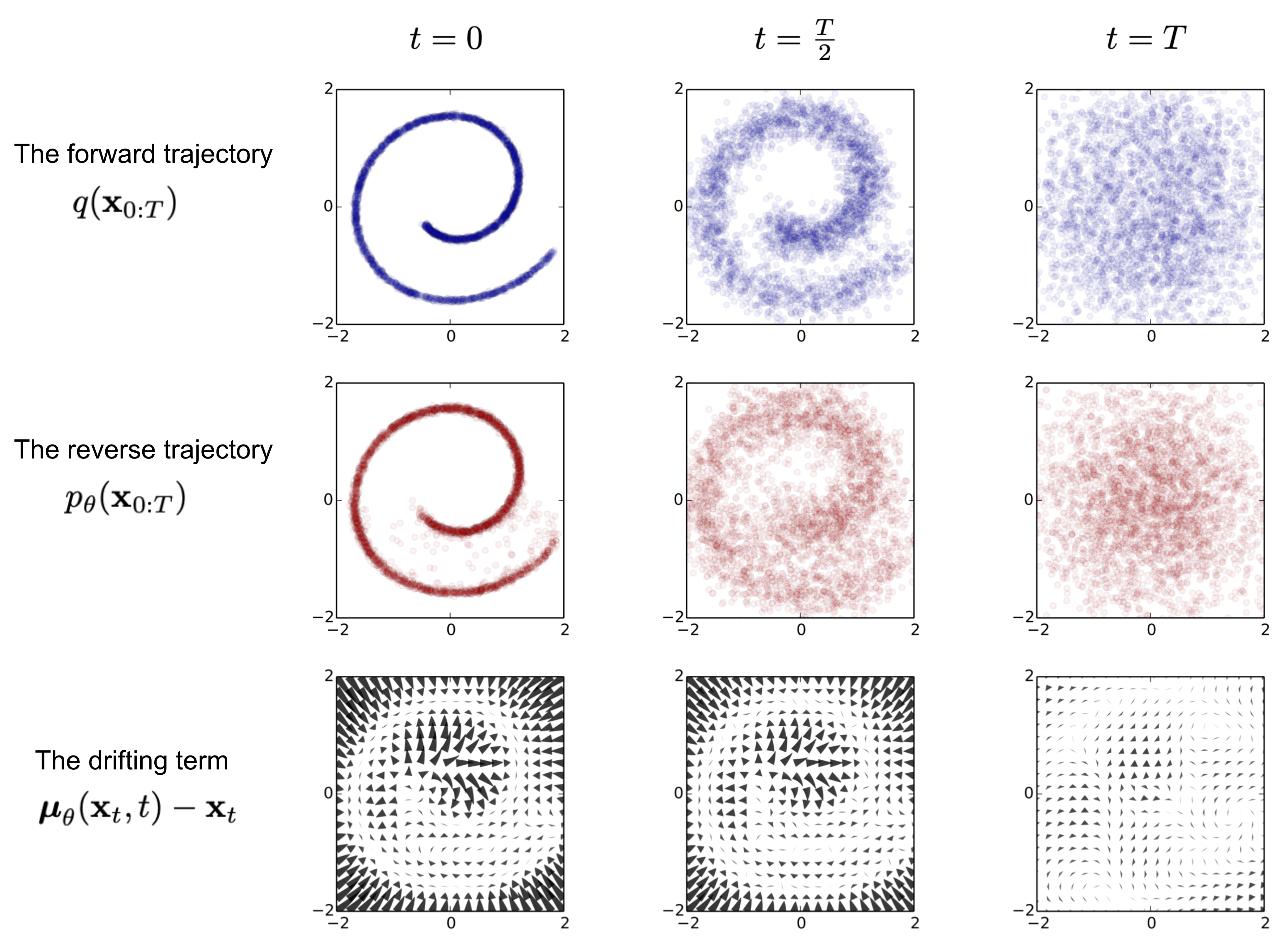
正向扩散过程

给定一个从真实数据分布中采样的数据点$\mathbf{x}_0 \sim q(\mathbf{x})$，我们定义一个正向扩散过程，其中我们在$T$步中向样本中添加少量高斯噪声，产生一系列噪声样本$\mathbf{x}_1, \dots, \mathbf{x}_T$。步长由方差调度$\{\beta_t \in (0, 1)\}_{t=1}^T$控制。

$$ q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \quad q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) $$

随着步骤$t$变大，数据样本$\mathbf{x}_0$逐渐失去其可辨识的特征。最终，当$T \to \infty$时，$\mathbf{x}_T$等同于各向同性高斯分布。

图2. 通过慢慢添加（移除）噪声生成样本的正向（逆向）扩散过程的马尔可夫链。（图片来源：Ho等，2020，附加了一些注释）

上述过程的一个好处是，我们可以使用重新参数化技巧在任何任意时间步$t$以闭合形式采样$\mathbf{x}_t$。设$\alpha_t = 1 - \beta_t$和$\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$：

$$ \begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned} $$

(*) 回想一下，当我们合并两个具有不同方差的高斯分布$\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I})$和$\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I})$时，新分布为$\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I})$。这里合并的标准差为$\sqrt{(1 - \alpha_t) + \alpha_t (1-\alpha_{t-1})} = \sqrt{1 - \alpha_t\alpha_{t-1}}$。

通常，当样本变得更嘈杂时，我们可以负担得起更大的更新步长，所以$\beta_1 < \beta_2 < \dots < \beta_T$因此$\bar{\alpha}_1 > \dots > \bar{\alpha}_T$。

与随机梯度朗之万动力学的联系

朗之万动力学是物理学中的一个概念，专为统计建模分子系统而开发。结合随机梯度下降，随机梯度朗之万动力学(Welling & Teh 2011)可以使用马尔可夫链中的更新中的梯度$\nabla_\mathbf{x} \log p(\mathbf{x})$来生成概率密度$p(\mathbf{x})$的样本：

$$ \mathbf{x}_t = \mathbf{x}_{t-1} + \frac{\delta}{2} \nabla_\mathbf{x} \log p(\mathbf{x}_{t-1}) + \sqrt{\delta} \boldsymbol{\epsilon}_t ,\quad\text{where } \boldsymbol{\epsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) $$

其中$\delta$是步长。当$T \to \infty, \epsilon \to 0$，$\mathbf{x}_T$等于真实的概率密度$p(\mathbf{x})$。

与标准SGD相比，随机梯度朗之万动力学将高斯噪声注入参数更新中，以避免陷入局部最小值。

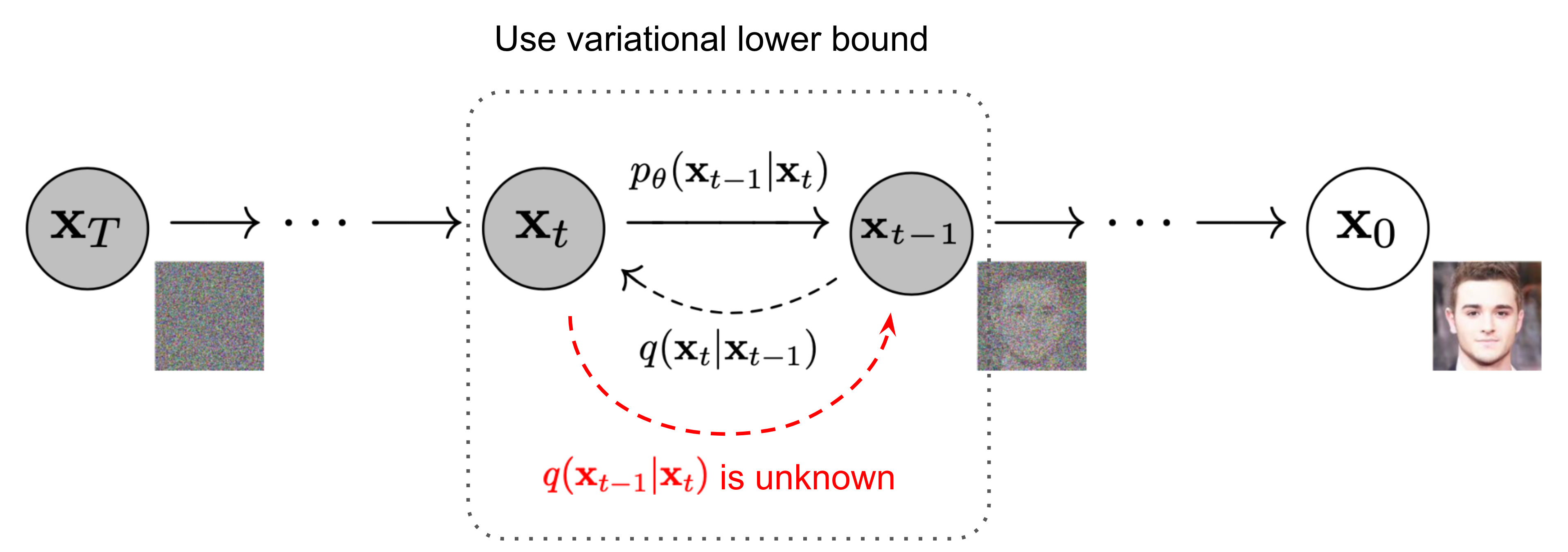
逆向扩散过程

如果我们能够逆转上述过程并从$q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)$中采样，我们将能够从高斯噪声输入$\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$重新创建真实样本。请注意，如果$\beta_t$足够小，$q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)$也将是高斯分布。不幸的是，我们无法轻松估计$q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)$，因为它需要使用整个数据集，因此我们需要学习一个模型$p_\theta$来*似这些条件概率，以便运行逆向扩散过程。

$$ p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) $$

图3. 训练扩散模型以模拟2D瑞士卷数据的示例。（图片来源：Sohl-Dickstein等，2015）

值得注意的是，当以$\mathbf{x}_0$为条件时，逆向条件概率是可处理的：

$$ q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), \color{red}{\tilde{\beta}_t} \mathbf{I}) $$

使用贝叶斯规则，我们有：

$$ \begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{aligned} $$

其中$C(\mathbf{x}_t, \mathbf{x}_0)$是某些不涉及$\mathbf{x}_{t-1}$的函数，细节被省略了。按照标准高斯密度函数，均值和方差可以参数化如下（回想一下$\alpha_t = 1 - \beta_t$和$\bar{\alpha}_t = \prod_{i=1}^T \alpha_i$）：

$$ \begin{aligned} \tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}) = \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\ &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned} $$

由于良好的性质，我们可以表示$\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t)$并将其代入上述方程得到：

$$ \begin{aligned} \tilde{\boldsymbol{\mu}}_t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\ &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \end{aligned} $$

如图2所示，这种设置与VAE非常相似，因此我们可以使用变分下界优化负对数似然。

$$ \begin{aligned} - \log p_\theta(\mathbf{x}_0) &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) \\ &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\ &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\ &= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ \text{Let }L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \end{aligned} $$

同样使用詹森不等式可以很容易得到相同的结果。假设我们希望将交叉熵最小化作为学习目标，

$$ \begin{aligned} L_\text{CE} &= - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \mathbb{E}_{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big) \\ &\leq - \mathbb{E}_{q(\mathbf{x}_{0:T})} \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \\ &= \mathbb{E}_{q(\mathbf{x}_{0:T})}\Big[\log \frac{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] = L_\text{VLB} \end{aligned} $$

为了将方程中的每一项转换为可解析的，我们可以将目标进一步重写为若干KL散度和熵项的组合（详见Sohl-Dickstein等，2015的附录B中的详细步骤）：

$$ \begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\ &= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \end{aligned} $$

让我们分别标记变分下界损失中的每个组件：

$$ \begin{aligned} L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\ \text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\ L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\ L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \end{aligned} $$

$L_\text{VLB}$中的每个KL项（除了$L_0$）比较两个高斯分布，因此它们可以在闭合形式中计算。$L_T$是常数，在训练过程中可以忽略，因为$q$没有可学习的参数，并且$\mathbf{x}_T$是高斯噪声。Ho等，2020使用从$\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))$派生的单独的离散解码器来建模$L_0$。

用于训练损失的$L_t$的参数化

回想一下，我们需要学习一个神经网络来*似逆向扩散过程中的条件概率分布，$p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_theta(\mathbf{x}_t, t))。我们希望训练$\boldsymbol{\mu}_theta$来预测$\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)$。因为$\mathbf{x}_t$在训练时可作为输入，所以我们可以重新参数化高斯噪声项，使其根据时间步$t$从输入$\mathbf{x}_t$预测$\boldsymbol{\epsilon}_t$：

$$ \begin{aligned} \boldsymbol{\mu}_theta(\mathbf{x}_t, t) &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t) \Big)} \\ \text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_theta(\mathbf{x}_t, t)) \end{aligned} $$

损失项$L_t$被参数化以最小化与$\tilde{\boldsymbol{\mu}}$的差异：

$$ \begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned} $$

简化

经验上，Ho等（2020）发现训练扩散模型在忽略加权项的简化目标下效果更好：

$$ \begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldboldsymbol{\epsilon}_theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldboldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned} $$

最终的简化目标是：

$$ L_\text{simple} = L_t^\text{simple} + C $$

其中$C$是一个不依赖于$\theta$的常数。

图4. DDPM中的训练和采样算法（图片来源：Ho等，2020）

与噪声条件得分网络（NCSN）的联系

Song & Ermon (2019) 提出了一种基于分数的生成建模方法，通过使用通过分数匹配估计的数据分布的梯度，通过Langevin动力学生成样本。每个样本$\mathbf{x}$的密度概率的分数定义为其梯度$\nabla_{\mathbf{x}} \log q(\mathbf{x})$。分数网络$\mathbf{s}_\theta: \mathbb{R}^D \to \mathbb{R}^D$被训练用来估计它，$\mathbf{s}_\theta(\mathbf{x}) \approx \nabla_{\mathbf{x}} \log q(\mathbf{x})$。

为了使其在深度学习环境下可扩展到高维数据，他们提出使用去噪分数匹配（Vincent, 2011）或切片分数匹配（使用随机投影；Song等，2019）。去噪分数匹配向数据添加预定的小噪声$q(\tilde{\mathbf{x}} \vert \mathbf{x})$并通过分数匹配估计$q(\tilde{\mathbf{x}})$。

回顾一下，Langevin动力学可以使用分数$\nabla_{\mathbf{x}} \log q(\mathbf{x})$在迭代过程中从概率密度分布中采样数据点。

然而，根据流形假设，大多数数据预计集中在低维流形中，尽管观察到的数据看起来可能是任意高维的。这对分数估计产生了负面影响，因为数据点无法覆盖整个空间。在数据密度较低的区域，分数估计不那么可靠。加入少量高斯噪声以使扰动数据分布覆盖整个空间$\mathbb{R}^D$后，分数估计网络的训练变得更加稳定。Song & Ermon (2019)通过以不同级别的噪声扰动数据并训练一个噪声条件分数网络来联合估计所有不同噪声级别的扰动数据的分数。

增加噪声级别的时间表类似于前向扩散过程。如果我们使用扩散过程的标注，分数*似为$\mathbf{s}_\theta(\mathbf{x}_t, t) \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t)$。假设一个高斯分布$\mathbf{x} \sim \mathcal{N}(\mathbf{\mu}, \sigma^2 \mathbf{I})$，我们可以将其密度函数对数的导数写为$\nabla_{\mathbf{x}}\log p(\mathbf{x}) = \nabla_{\mathbf{x}} \Big(-\frac{1}{2\sigma^2}(\mathbf{x} - \boldsymbol{\mu})^2 \Big) = - \frac{\mathbf{x} - \boldsymbol{\mu}}{\sigma^2} = - \frac{\boldsymbol{\epsilon}}{\sigma}$，其中$\boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{0}, \mathbf{I})$。回顾一下，$q(\mathbf{x}_t \vert \mathbf{x}_0) \sim \mathcal{N}(\sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I})$因此，

$$ \mathbf{s}_\theta(\mathbf{x}_t, t) \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \mathbb{E}_{q(\mathbf{x}_0)} [\nabla_{\mathbf{x}_t} q(\mathbf{x}_t \vert \mathbf{x}_0)] = \mathbb{E}_{q(\mathbf{x}_0)} \Big[ - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}} \Big] = - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}} $$

$\beta_t$的参数化

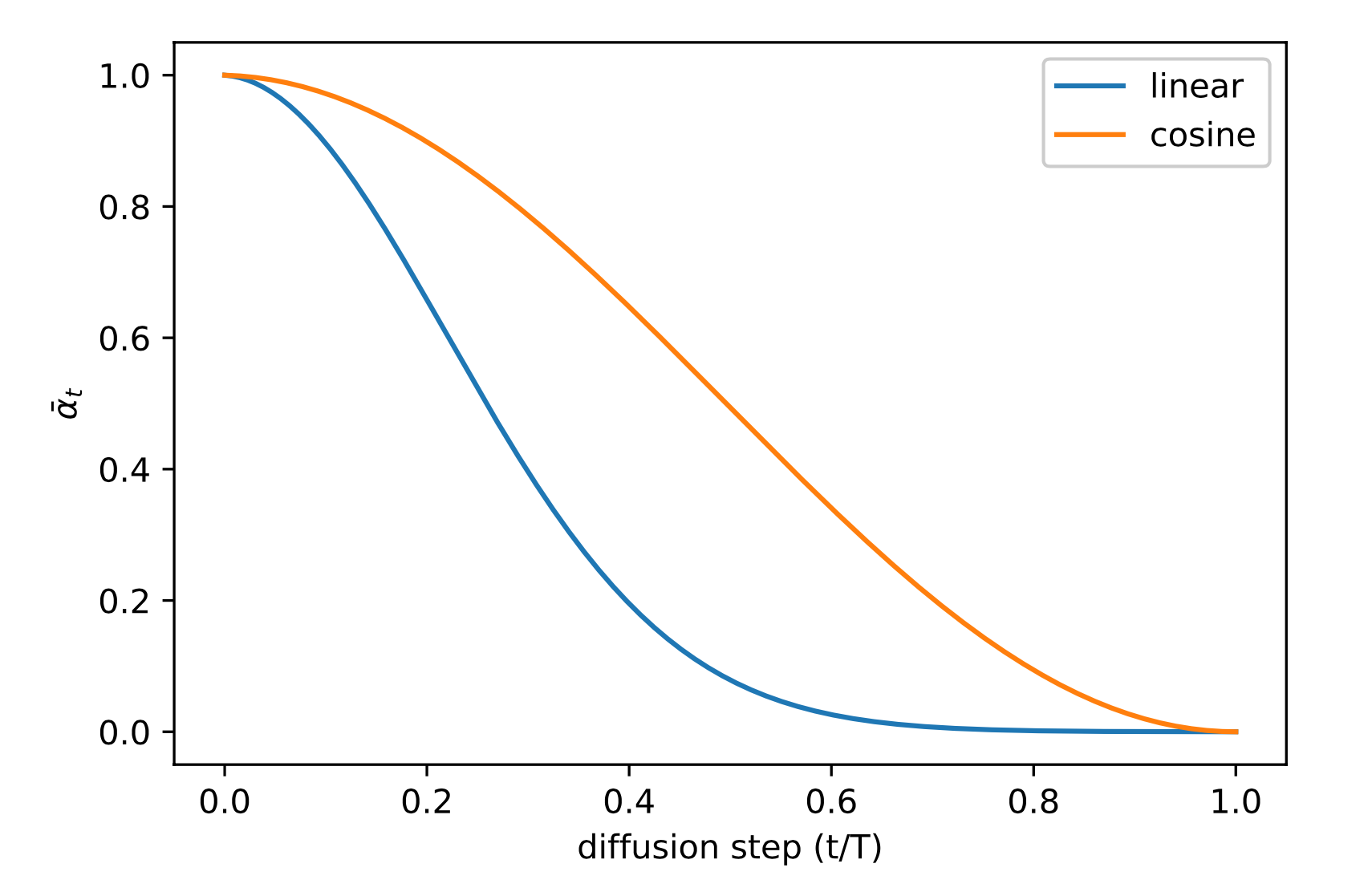
在Ho等人（2020）中，前向方差被设定为一系列线性增加的常数，从$\beta_1=10^{-4}$到$\beta_T=0.02$。与标准化的图像像素值在$[-1, 1]$之间相比，它们相对较小。尽管他们的实验中扩散模型显示了高质量的样本，但仍无法达到其他生成模型的竞争性模型对数似然。

Nichol & Dhariwal（2021）提出了一些改进技术，以帮助扩散模型获得更低的NLL。其中一项改进是使用基于余弦的方差时间表。时间表函数的选择可以是任意的，只要它在训练过程中间提供接**滑的下降，并在$t=0$和$t=T$附*的变化很小。

$$ \beta_t = \text{clip}(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999) \quad\bar{\alpha}_t = \frac{f(t)}{f(0)}\quad\text{where }f(t)=\cos\Big(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2}\Big)^2 $$

其中小偏移$s$是为了防止$\beta_t$在接*$t=0$时变得太小。

图5. 训练期间线性和基于余弦的$\beta_t$时间表比较。（图片来源：Nichol & Dhariwal，2021）

反向过程方差$\boldsymbol{\Sigma}_\theta$的参数化

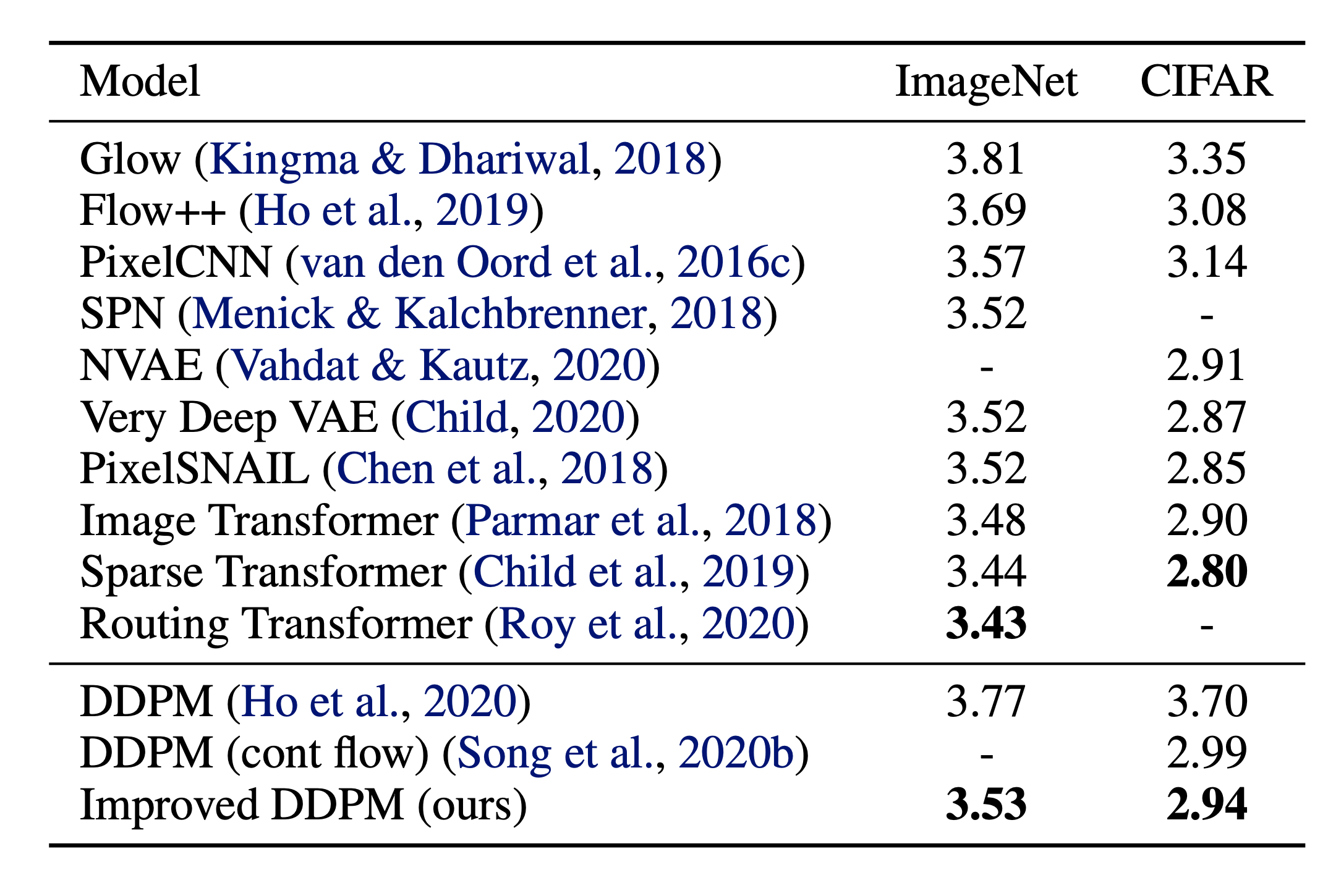
Ho等人（2020）选择将$\beta_t$固定为常数，而不是使它们可学习，并将$\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \sigma^2_t \mathbf{I}$设定为常数，其中$\sigma_t$不是可学习的，而是设定为$\beta_t$或$\tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t$。因为他们发现学习对角方差$\boldsymbol{\Sigma}_\theta$会导致训练不稳定和样本质量下降。

Nichol & Dhariwal（2021）提出学习$\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)$作为$\beta_t$和$\tilde{\beta}_t$之间的插值，通过模型预测一个混合向量$\mathbf{v}$ ：

$$ \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t) $$

然而，简单目标$L_\text{simple}$不依赖于$\boldsymbol{\Sigma}_\theta$。为了增加依赖性，他们构建了一个混合目标$L_\text{hybrid} = L_\text{simple} + \lambda L_\text{VLB}$，其中$\lambda=0.001$很小，并且在$L_\text{VLB}$项中停止了$\boldsymbol{\mu}_\theta$的梯度，因此$L_\text{VLB}$只引导$\boldsymbol{\Sigma}_\theta$的学习。经验表明，$L_\text{VLB}$很难优化，可能是由于梯度噪声，因此他们提出使用带有重要采样的时间*均*滑版本的$L_\text{VLB}$。

图6. 改进DDPM与其他基于似然生成模型的负对数似然比较。NLL以比特/维度为单位报告。（图片来源：Nichol & Dhariwal，2021）

条件生成

在带有条件信息（如ImageNet数据集）的图像上训练生成模型时，通常会生成条件在类别标签或一段描述性文本上的样本。

分类器引导的扩散

为了在扩散过程中显式地结合类别信息，Dhariwal & Nichol（2021）在带有噪声的图像$\mathbf{x}_t$上训练了一个分类器$f_\phi(y \vert \mathbf{x}_t, t)$，并使用梯度$\nabla_\mathbf{x} \log f_\phi(y \vert \mathbf{x}_t)$引导扩散采样过程朝向条件信息$y$（例如目标类别标签），通过改变噪声预测。回顾一下，$\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)$我们可以将联合分布$q(\mathbf{x}_t, y)$的分数函数写成如下形式：

$$ \begin{aligned} \bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t) \end{aligned} $$

为了控制分类器引导的强度，我们可以在delta部分添加一个权重$w$，

$$ \bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} \; w \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t) $$

得到的消融扩散模型（ADM）和带有附加分类器引导的模型（ADM-G）能够比现有最先进的生成模型（例如BigGAN）取得更好的结果。

图7. 这些算法使用分类器的引导在DDPM和DDIM中运行条件生成。（图片来源：Dhariwal & Nichol，2021）

此外，通过对U-Net架构的一些修改，Dhariwal & Nichol（2021）展示了在扩散模型上比GAN更好的表现。架构修改包括更大的模型深度/宽度，更多的注意头，多分辨率注意力，BigGAN残差块用于上/下采样，残差连接重新缩放为$1/\sqrt{2}$和自适应组归一化（AdaGN）。

无分类器引导

在没有独立分类器$f_\phi$的情况下，通过结合条件和无条件扩散模型的分数，仍然可以运行条件扩散步骤（Ho & Salimans，2021）。设无条件去噪扩散模型$p_\theta(\mathbf{x})$通过分数估计器$\boldsymbol{\epsilon}_theta(\mathbf{x}_t, t)$进行参数化，而条件模型$p_\theta(\mathbf{x} \vert y)$通过$\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y)$进行参数化。这两个模型可以通过一个神经网络来学习。具体来说，一个条件扩散模型$p_\theta(\mathbf{x} \vert y)$在成对数据$(\mathbf{x}, y)$上训练，其中条件信息$y$会在随机的时间段被丢弃，这样模型也知道如何无条件生成图像，即$\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y=\varnothing)$。

隐式分类器的梯度可以通过条件和无条件分数估计器表示。一旦插入分类器引导的修改分数，分数就不再依赖于单独的分类器。

$$ \begin{aligned} \nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t) &= \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \vert y) - \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) \\ &= - \frac{1}{\sqrt{1 - \bar{\alpha}_t}}\Big( \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t) \Big) \\ \bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t, y) &= \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t, y) - \sqrt{1 - \bar{\alpha}_t} \; w \nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t) \\ &= \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t, y) + w \big(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_theta(\mathbf{x}_t, t) \big) \\ &= (w+1) \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - w \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \end{aligned} $$

他们的实验表明，无分类器引导可以在FID（区分合成和生成图像）和IS（质量和多样性）之间实现良好的*衡。

引导扩散模型GLIDE（Nichol, Dhariwal & Ramesh, et al. 2022）探讨了两种引导策略，CLIP引导和无分类器引导，并发现后者更受欢迎。他们假设这是因为CLIP引导通过对CLIP模型的对抗性示例利用模型，而不是优化更匹配的图像生成。

加速扩散模型

通过遵循反向扩散过程的马尔可夫链从DDPM生成一个样本非常慢，因为$T$可以达到一千步甚至几千步。Song等人（2020）的一个数据点：“例如，从DDPM采样50k张32 × 32大小的图像大约需要20小时，而在Nvidia 2080 Ti GPU上用GAN不到一分钟。”

减少采样步骤与蒸馏

一种简单的方法是运行跨步采样计划（Nichol & Dhariwal, 2021），通过每隔$\lceil T/S \rceil$步进行采样更新，将过程从$T$步减少到$S$步。生成的新采样计划是$\{\tau_1, \dots, \tau_S\}$，其中$\tau_1 < \tau_2 < \dots < \tau_S \in [1, T]$且$S < T$。

另一种方法是将$q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)$根据nice property重新参数化为期望的标准偏差$\sigma_t$：

$$ \begin{aligned} \mathbf{x}_{t-1} &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1}}\boldsymbol{\epsilon}_{t-1} & \\ &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \boldsymbol{\epsilon}_t + \sigma_t\boldsymbol{\epsilon} & \\ &= \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t) + \sigma_t\boldsymbol{\epsilon} \\ q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \mathbf{I}) \end{aligned} $$

其中模型$\epsilon^{(t)}_\theta(.)$从$\mathbf{x}_t$预测$\epsilon_t$。

回顾一下$q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I})$，因此我们有：

$$ \tilde{\beta}_t = \sigma_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t $$

让$\sigma_t^2 = \eta \cdot \tilde{\beta}_t$，这样我们可以将$\eta \in \mathbb{R}^+$作为超参数来控制采样随机性。$\eta = 0$的特例使采样过程确定性。这种模型称为去噪扩散隐式模型（DDIM；Song等人，2020）。DDIM具有相同的边际噪声分布，但确定性地将噪声映射回原始数据样本。

在生成过程中，我们不必遵循整个链$t=1,\dots,T$，而是一个步骤的子集。让我们用$s < t$表示这个加速轨迹中的两个步骤。DDIM更新步骤为：

$$ q_{\sigma, s < t}(\mathbf{x}_s \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_s; \sqrt{\bar{\alpha}_s} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_s - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \mathbf{I}) $$

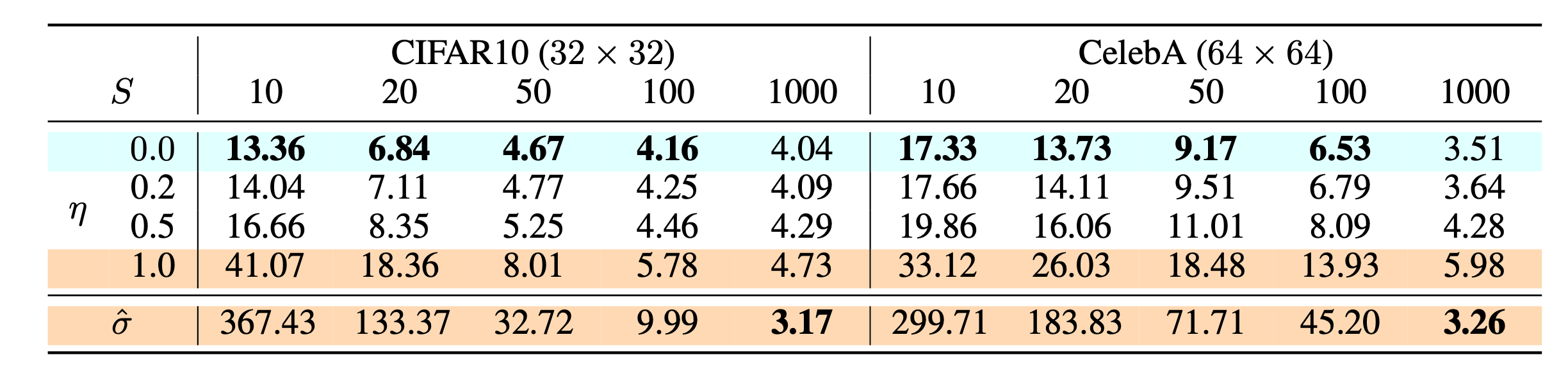
在实验中，所有模型都使用$T=1000$的扩散步骤进行训练，但他们观察到DDIM（$\eta=0$）在$S$较小时可以产生最佳质量样本，而DDPM（$\eta=1$）在$S$较小时表现更差。DDPM确实在我们能够运行完整的反向马尔可夫扩散步骤（$S=T=1000$）时表现更好。使用DDIM，可以将扩散模型训练到任意数量的前向步骤，但在生成过程中只从步骤的子集中采样。

图8. 在CIFAR10和CelebA数据集上不同设置的扩散模型的FID分数，包括$\color{cyan}{\text{DDIM}}$ ($\eta=0$)和$\color{orange}{\text{DDPM}}$ ($\hat{\sigma}$)。（图片来源：Song等人，2020）

与DDPM相比，DDIM能够：

使用更少的步骤生成更高质量的样本。
具有“一致性”属性，因为生成过程是确定性的，这意味着多个样本在相同的潜在变量条件下应具有相似的高级特征。
由于一致性，DDIM可以在潜在变量中进行语义上有意义的插值。

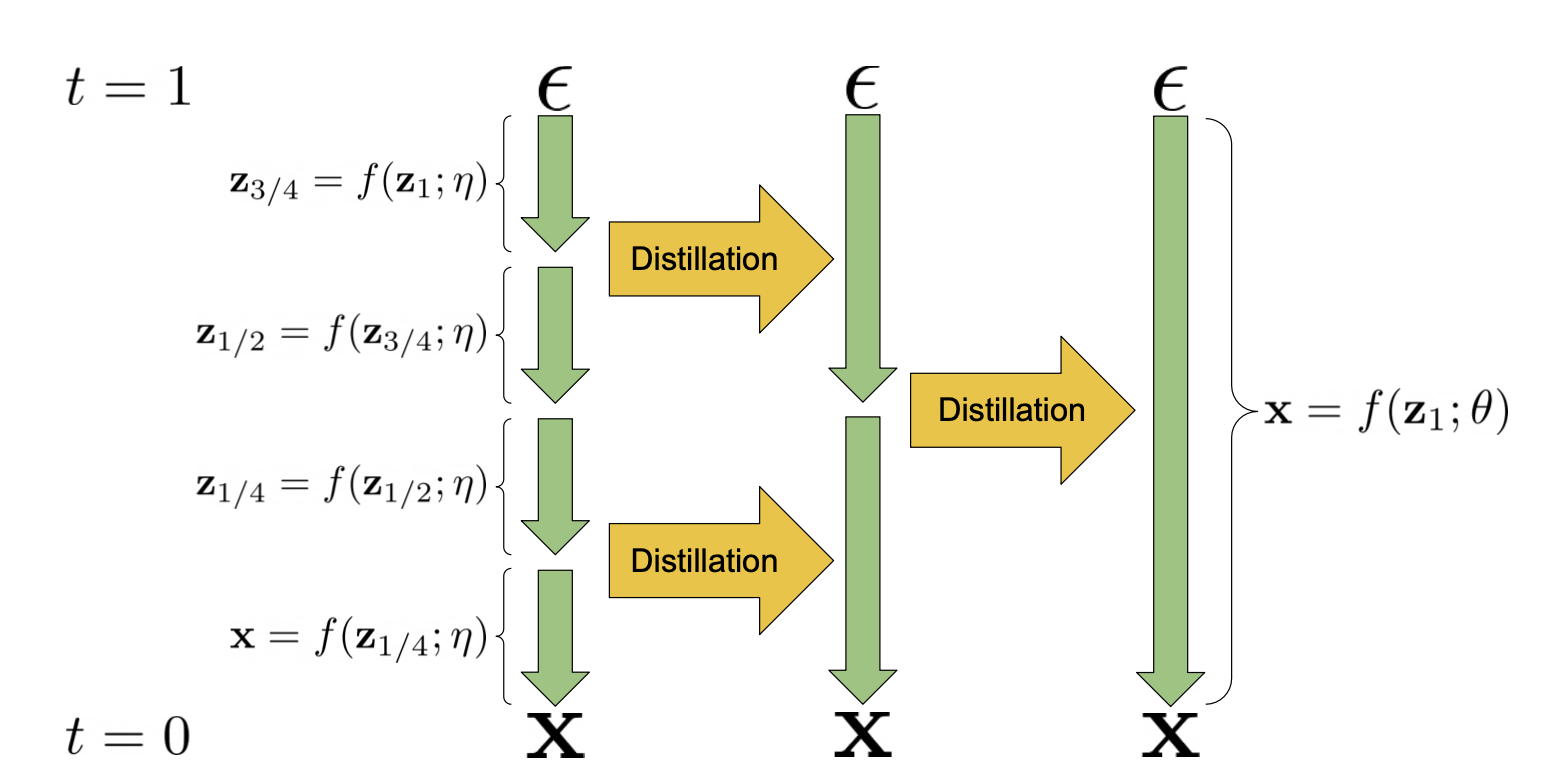
图9. 渐进蒸馏可以在每次迭代中将扩散采样步骤减少一半。（图片来源：Salimans & Ho, 2022）

渐进蒸馏（Salimans & Ho, 2022）是一种将训练好的确定性采样器蒸馏到新的减少一半采样步骤的模型中的方法。学生模型从教师模型初始化并向目标去噪，其中一个学生DDIM步骤匹配2个教师步骤，而不是使用原始样本$\mathbf{x}_0$作为去噪目标。在每次渐进蒸馏迭代中，我们可以将采样步骤减半。

图10. 并列比较算法1（扩散模型训练）和算法2（渐进蒸馏），渐进蒸馏中的相对变化以绿色突出显示。
（图片来源：Salimans & Ho, 2022）

一致性模型（Song等人，2023）学习将扩散采样轨迹上的任何中间噪声数据点$\mathbf{x}_t, t > 0$直接映射回其原点$\mathbf{x}_0$。它被称为一致性模型，因为其自一致性属性，即轨迹上的任何数据点都映射到相同的原点。

图11. 一致性模型学习将轨迹上的任何数据点映射回其原点。（图片来源：Song等人，2023）

给定轨迹$\{\mathbf{x}_t \vert t \in [\epsilon, T]\}$，一致性函数$f$定义为$f: (\mathbf{x}_t, t) \mapsto \mathbf{x}_\epsilon$，且方程$f(\mathbf{x}_t, t) = f(\mathbf{x}_{t’}, t’)=\mathbf{x}_\epsilon$在所有$t, t’ \in [\epsilon, T]$时成立。当$t=\epsilon$时，$f$是一个恒等函数。模型可以参数化如下，其中$c_\text{skip}(t)$和$c_\text{out}(t)$函数的设计方式是$c_\text{skip}(\epsilon) = 1, c_\text{out}(\epsilon) = 0$：

$$ f_\theta(\mathbf{x}, t) = c_\text{skip}(t)\mathbf{x} + c_\text{out}(t) F_\theta(\mathbf{x}, t) $$

一致性模型有可能在单步中生成样本，同时仍保持通过多步采样过程权衡计算与质量的灵活性。

论文介绍了两种训练一致性模型的方法：

一致性蒸馏（CD）：通过最小化从相同轨迹生成的模型输出之间的差异，将扩散模型蒸馏到一致性模型中。这使得评估采样更加便宜。一致性蒸馏损失为：

$$ \begin{aligned} \mathcal{L}^N_\text{CD} (\theta, \theta^-; \phi) &= \mathbb{E} [\lambda(t_n)d(f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1}), f_{\theta^-}(\hat{\mathbf{x}}^\phi_{t_n}, t_n)] \\ \hat{\mathbf{x}}^\phi_{t_n} &= \mathbf{x}_{t_{n+1}} - (t_n - t_{n+1}) \Phi(\mathbf{x}_{t_{n+1}}, t_{n+1}; \phi) \end{aligned} $$

其中
- $\Phi(.;\phi)$是一步ODE求解器的更新函数；
- $n \sim \mathcal{U}[1, N-1]$，在$1,\dots, N-1$上具有均匀分布；
- 网络参数$\theta^-$是$\theta$的EMA版本，这大大稳定了训练（就像在DQN或动量对比学习中一样）；
- $d(.,.)$是一个满足$\forall \mathbf{x}, \mathbf{y}: d(\mathbf{x}, \mathbf{y}) \leq 0$且$d(\mathbf{x}, \mathbf{y})=0$当且仅当$\mathbf{x}=\mathbf{y}$的正距离度量函数，如$\ell_2$，$\ell_1$或LPIPS（学习的感知图像补丁相似性）距离；
- $\lambda(.) \in \mathbb{R}^+$是一个正权函数，论文设置$\lambda(t_n)=1$。
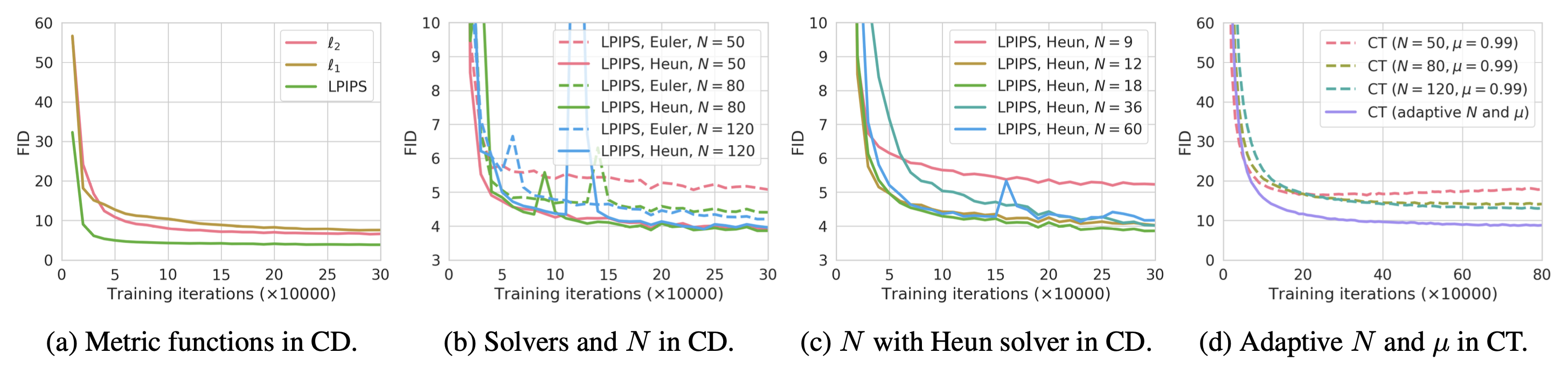
一致性训练（CT）：另一种选择是独立训练一致性模型。注意，在CD中，使用预训练的分数模型$s_\phi(\mathbf{x}, t)$来*似地面真值分数$\nabla\log p_t(\mathbf{x})$，但在CT中，我们需要一种方法来估计这个分数函数，事实证明，存在$\nabla\log p_t(\mathbf{x})$的无偏估计器，即$-\frac{\mathbf{x}_t - \mathbf{x}}{t^2}$。CT损失定义如下：

$$ \mathcal{L}^N_\text{CT} (\theta, \theta^-; \phi) = \mathbb{E} [\lambda(t_n)d(f_\theta(\mathbf{x} + t_{n+1} \mathbf{z},\;t_{n+1}), f_{\theta^-}(\mathbf{x} + t_n \mathbf{z},\;t_n)] \text{ where }\mathbf{z} \in \mathcal{N}(\mathbf{0}, \mathbf{I}) $$

根据论文中的实验，他们发现，

Heun ODE求解器比Euler的一阶求解器效果更好，因为高阶ODE求解器在相同$N$下的估计误差较小。
在不同选项的距离度量函数$d(.)$中，LPIPS度量比$\ell_1$和$\ell_2$距离效果更好。
较小的$N$导致更快的收敛，但样本更差，而较大的$N$导致收敛速度较慢，但收敛后的样本更好。

图12. 不同配置下一致性模型的性能比较。CD的最佳配置是LPIPS距离度量、Heun ODE求解器和$N=18$。（图片来源：Song等人，2023）

潜变量空间

潜扩散模型（LDM；Rombach & Blattmann等人，2022）在潜空间而不是像素空间中运行扩散过程，从而降低训练成本并加快推理速度。其动机是观察到图像的大多数位元贡献于感知细节，而经过激进压缩后，语义和概念组成仍然保留。LDM通过首先用自编码器去除像素级冗余，然后在学习的潜变量上使用扩散过程进行语义概念的操纵/生成，松散地将感知压缩和语义压缩与生成建模学习分解。

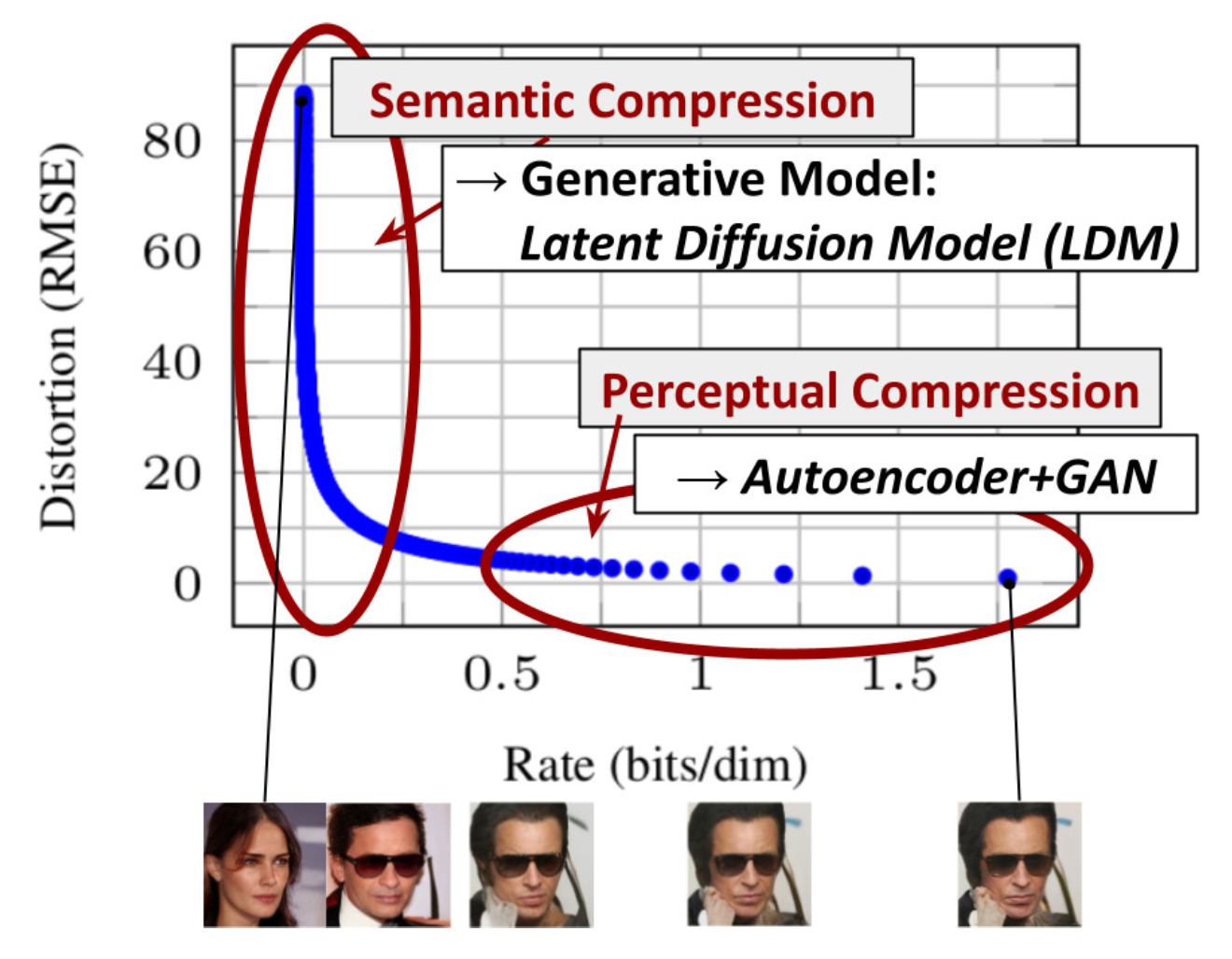
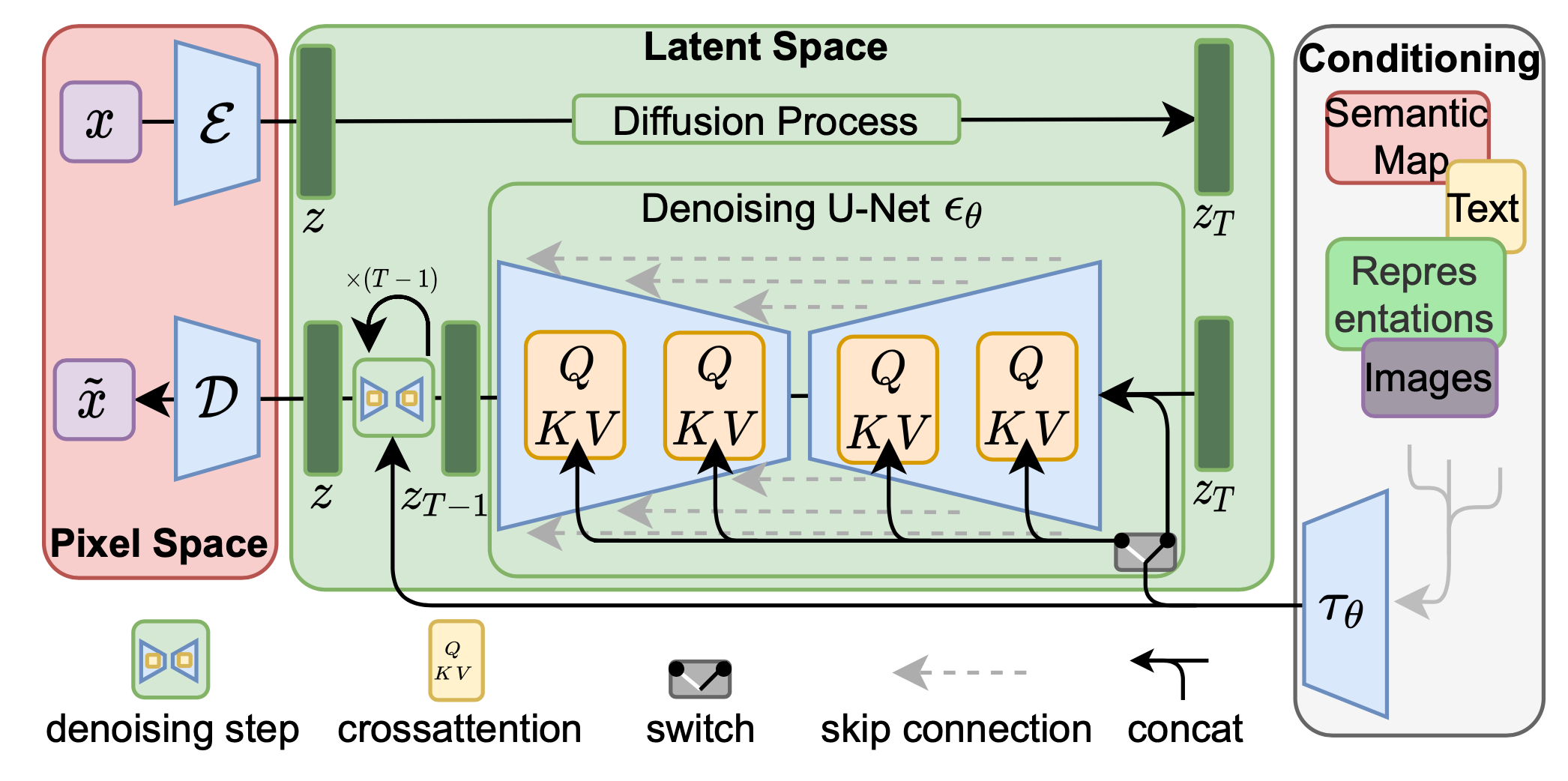
图13. 压缩率与失真之间权衡的图示，说明两阶段压缩——感知压缩和语义压缩。（图片来源：Rombach & Blattmann等人，2022）

感知压缩过程依赖于自编码器模型。一个编码器$\mathcal{E}$用于将输入图像$\mathbf{x} \in \mathbb{R}^{H \times W \times 3}$压缩到一个更小的二维潜向量$\mathbf{z} = \mathcal{E}(\mathbf{x}) \in \mathbb{R}^{h \times w \times c}$，其中下采样率$f=H/h=W/w=2^m, m \in \mathbb{N}$。然后一个解码器$\mathcal{D}$从潜向量重建图像，$\tilde{\mathbf{x}} = \mathcal{D}(\mathbf{z})$。论文探索了自编码器训练中的两种正则化方法以避免潜空间中的任意高方差。

KL-reg：对学习的潜变量施加一个小的KL惩罚，趋向标准正态分布，类似于VAE。
VQ-reg：在解码器内使用向量量化层，类似于VQVAE，但量化层被解码器吸收。

扩散和去噪过程发生在潜向量$\mathbf{z}$上。去噪模型是一个时间条件U-Net，增强了交叉注意力机制，以处理用于图像生成的灵活条件信息（例如类标签、语义图、图像的模糊变体）。这种设计等效于通过交叉注意力机制将不同模态的表示融合到模型中。每种类型的条件信息都配有一个特定领域的编码器$\tau_\theta$，将条件输入$y$投射到可以映射到交叉注意力组件的中间表示中，$\tau_\theta(y) \in \mathbb{R}^{M \times d_\tau}$：

$$ \begin{aligned} &\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\Big(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\Big) \cdot \mathbf{V} \\ &\text{where }\mathbf{Q} = \mathbf{W}^{(i)}_Q \cdot \varphi_i(\mathbf{z}_i),\; \mathbf{K} = \mathbf{W}^{(i)}_K \cdot \tau_\theta(y),\; \mathbf{V} = \mathbf{W}^{(i)}_V \cdot \tau_\theta(y) \\ &\text{and } \mathbf{W}^{(i)}_Q \in \mathbb{R}^{d \times d^i_\epsilon},\; \mathbf{W}^{(i)}_K, \mathbf{W}^{(i)}_V \in \mathbb{R}^{d \times d_\tau},\; \varphi_i(\mathbf{z}_i) \in \mathbb{R}^{N \times d^i_\epsilon},\; \tau_\theta(y) \in \mathbb{R}^{M \times d_\tau} \end{aligned} $$

图14. 潜扩散模型（LDM）的架构。（图片来源：Rombach & Blattmann等人，2022）

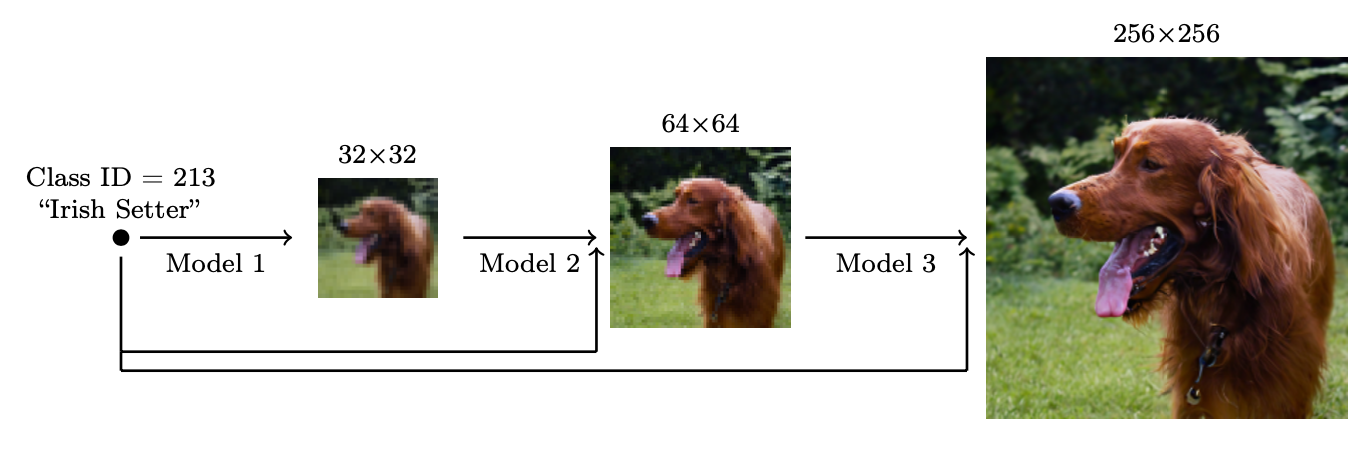
扩大生成分辨率和质量

为了生成高分辨率的高质量图像，Ho等人（2021）提出了使用多个扩散模型在增加的分辨率下的流水线。噪声条件增强是流水线模型之间最有效的，旨在对每个超分辨率模型$p_\theta(\mathbf{x} \vert \mathbf{z})$的条件输入$\mathbf{z}$应用强数据增强。条件噪声有助于减少流水线设置中的复合错误。U-net是扩散建模中用于高分辨率图像生成的常见选择。

图15. 在增加分辨率下的多个扩散模型的级联流水线。（图片来源：Ho等人，2021）

他们发现最有效的噪声是在低分辨率时应用高斯噪声，在高分辨率时应用高斯模糊。此外，他们还探索了两种需要对训练过程进行小修改的条件增强形式。注意，条件噪声仅在训练时应用，而不是在推理时。

截断条件增强在$t > 0$步骤早期停止扩散过程以实现低分辨率。
非截断条件增强运行全低分辨率反向过程直到步骤0，然后通过$\mathbf{z}_t \sim q(\mathbf{x}_t \vert \mathbf{x}_0)$来破坏它，然后将破坏的$\mathbf{z}_t$输入超分辨率模型。

两阶段扩散模型unCLIP（Ramesh等人，2022）大量利用CLIP文本编码器来生成高质量的文本引导图像。给定预训练的CLIP模型$\mathbf{c}$和扩散模型的成对训练数据$(\mathbf{x}, y)$，其中$x$是图像，$y$是相应的标题，我们可以计算CLIP文本和图像嵌入，$\mathbf{c}^t(y)$和$\mathbf{c}^i(\mathbf{x})$。unCLIP并行学习两个模型：

先验模型$P(\mathbf{c}^i \vert y)$：给定文本$y$输出CLIP图像嵌入$\mathbf{c}^i$。
解码器$P(\mathbf{x} \vert \mathbf{c}^i, [y])$：在给定CLIP图像嵌入$\mathbf{c}^i$和可选的原始文本$y$的条件下生成图像$\mathbf{x}$。

这些模型使条件生成成为可能，因为

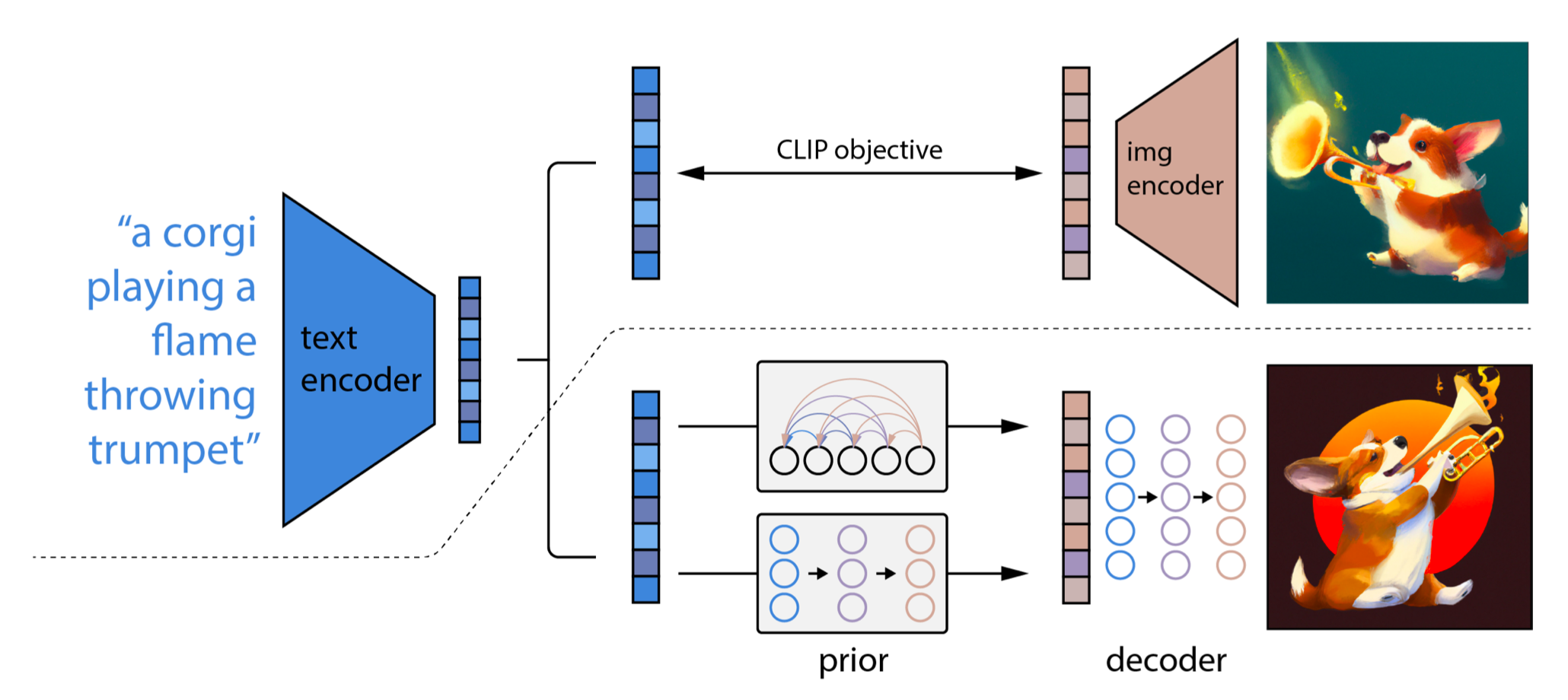
$$ \underbrace{P(\mathbf{x} \vert y) = P(\mathbf{x}, \mathbf{c}^i \vert y)}_{\mathbf{c}^i\text{ 是给定}\mathbf{x}\text{的确定性}} = P(\mathbf{x} \vert \mathbf{c}^i, y)P(\mathbf{c}^i \vert y) $$

图16. unCLIP的架构。（图片来源：Ramesh等人，2022）

unCLIP遵循两阶段图像生成过程：

给定文本$y$，首先使用CLIP模型生成文本嵌入$\mathbf{c}^t(y)$。使用CLIP潜在空间可以通过文本进行零样本图像操纵。
扩散或自回归先验$P(\mathbf{c}^i \vert y)$处理此CLIP文本嵌入以构建图像先验，然后扩散解码器$P(\mathbf{x} \vert \mathbf{c}^i, [y])$生成图像，条件在先验上。这个解码器还可以在图像输入的条件下生成图像变体，保留其风格和语义。

与CLIP模型不同，Imagen（Saharia等人，2022）使用预训练的大型LM（即冻结的T5-XXL文本编码器）来编码用于图像生成的文本。通常，模型尺寸越大，图像质量和文本-图像对齐越好。他们发现T5-XXL和CLIP文本编码器在MS-COCO上的性能相似，但在DrawBench（涵盖11个类别的提示集合）上，人类评估更喜欢T5-XXL。

在应用无分类器引导时，增加$w$可能会导致更好的图像-文本对齐但较差的图像保真度。他们发现这是由于训练-测试不匹配，即由于训练数据$\mathbf{x}$保持在$[-1, 1]$范围内，测试数据也应该如此。引入了两种阈值策略：

静态阈值：将$\mathbf{x}$预测裁剪到$[-1, 1]$
动态阈值：在每个采样步骤，计算$s$作为某个百分位数的绝对像素值；如果$s > 1$，将预测裁剪到$[-s, s]$并除以$s$。

Imagen在U-net中修改了几种设计，使其成为高效U-Net。

通过为较低分辨率添加更多残差锁，将模型参数从高分辨率块移到低分辨率；
将跳跃连接缩放为$1/\sqrt{2}$
将下采样（在卷积之前）和上采样操作（在卷积之后）的顺序反转，以提高前向传递的速度。

他们发现噪声条件增强、动态阈值和高效U-Net对图像质量至关重要，但缩放文本编码器大小比U-Net大小更重要。

模型架构

扩散模型有两种常见的骨干架构选择：U-Net和Transformer。

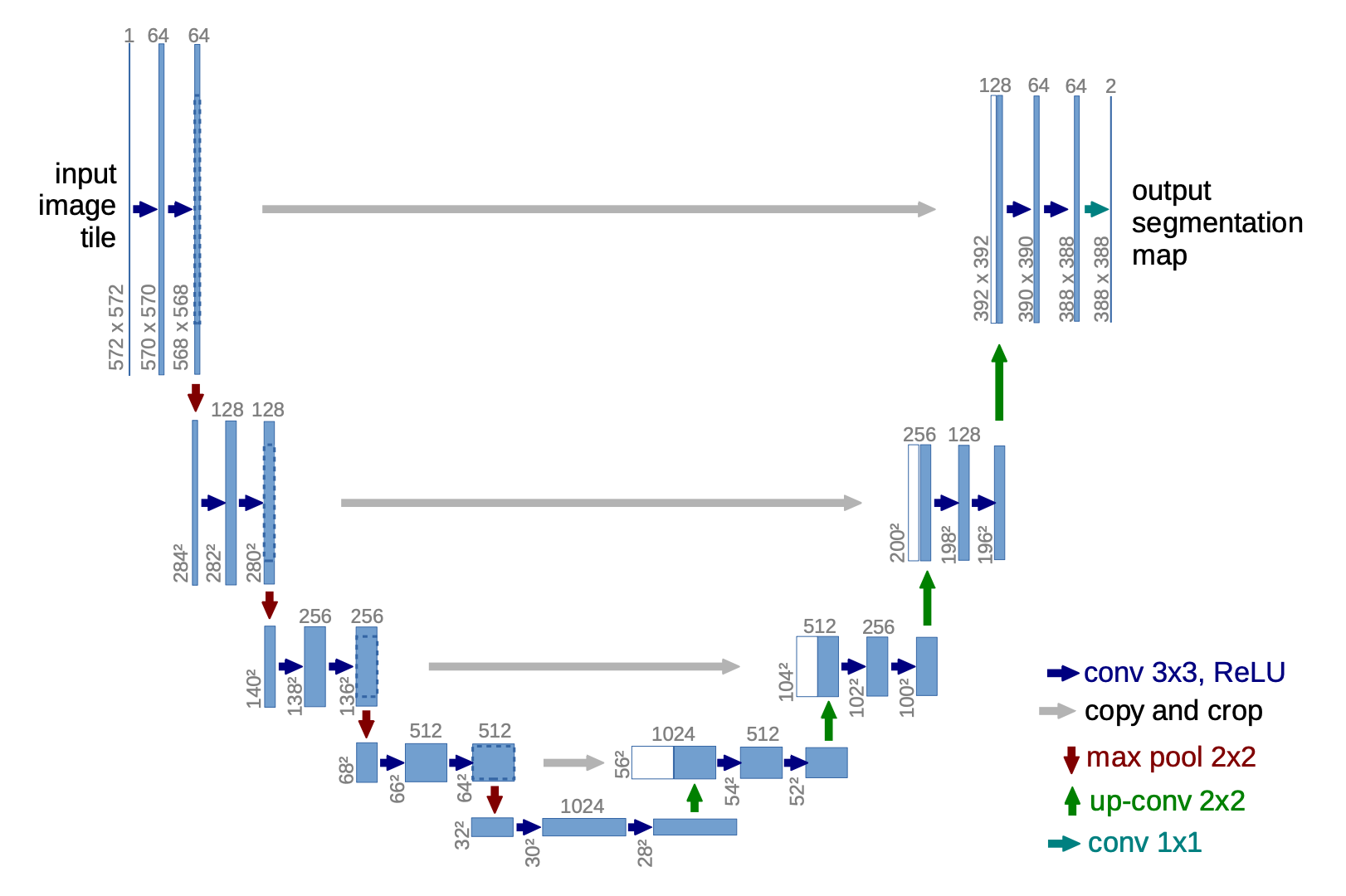
U-Net（Ronneberger等人，2015）由下采样堆栈和上采样堆栈组成。

下采样：每一步包括两次3x3卷积（无填充卷积）的重复应用，每次后跟一个ReLU和一个具有2步幅度的2x2最大池化。在每一步下采样时，特征通道的数量加倍。
上采样：每一步包括一个特征图的上采样，随后是一个2x2卷积，每次减半特征通道数量。
快捷方式：快捷连接将高分辨率特征提供给上采样过程。

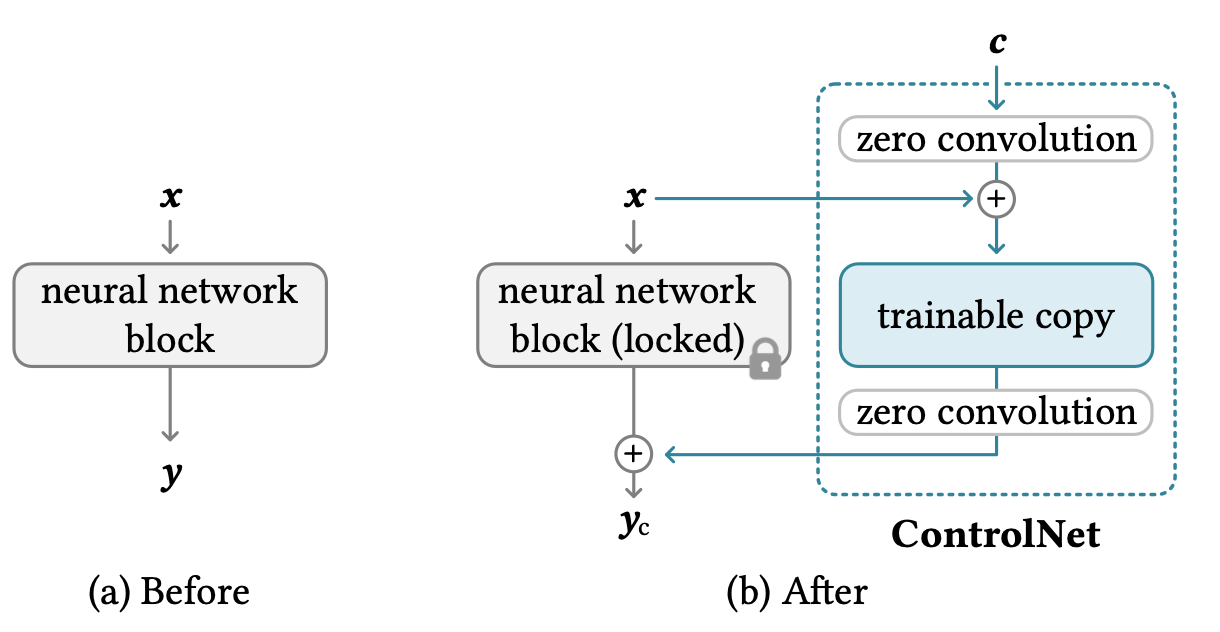
图17. U-net架构。每个蓝色方块是一个特征图，顶部标有通道数，左下角标有高度x宽度维度。灰色箭头标记快捷连接。（图片来源：Ronneberger，2015）

为了使图像生成以额外图像为条件进行组合信息如Canny边缘、Hough线、用户涂鸦、人体姿势骨架、分割图、深度和法线，ControlNet（Zhang等人，2023通过在U-Net的每个编码器层中添加“夹心”零卷积层，将原始模型权重的可训练副本引入架构中进行架构变化。具体而言，给定神经网络块$\mathcal{F}_\theta(.)$，ControlNet执行以下操作：

首先，冻结原始块的参数$\theta$
将其克隆为带有可训练参数$\theta_c$的副本和额外的条件向量$\mathbf{c}$。
使用两个零卷积层，表示为$\mathcal{Z}_{\theta_{z1}}(.;.)$和$\mathcal{Z}_{\theta_{z2}}(.;.)$，即1x1卷积层，权重和偏置都初始化为零，将这两个块连接起来。零卷积在初始训练步骤中通过消除随机噪声作为梯度来保护此骨干。
最终输出为：$\mathbf{y}_c = \mathcal{F}_\theta(\mathbf{x}) + \mathcal{Z}_{\theta_{z2}}(\mathcal{F}_{\theta_c}(\mathbf{x} + \mathcal{Z}_{\theta_{z1}}(\mathbf{c})))$

图18. ControlNet架构。（图片来源：Zhang等人，2023）

扩散Transformer（DiT；Peebles & Xie，2023）用于扩散建模在潜变量块上运行，使用与LDM（潜扩散模型）相同的设计空间。DiT有以下设置：

将输入的潜表示$\mathbf{z}$作为DiT的输入。
将大小为$I \times I \times C$的噪声潜变量“块化”为大小为$p$的块，并将其转换为大小为$(I/p)^2$的块序列。
然后这个块序列通过Transformer块。他们在探索如何在时间步$t$或类标签$c$等上下文信息的条件下进行生成的三种不同设计。在三种设计中，adaLN（自适应层归一化）-Zero效果最好，优于上下文内条件和交叉注意力块。比例和偏移参数$\gamma$和$\beta$是从$t$和$c$的嵌入向量之和回归出来的。尺度参数$\alpha$也是回归的，并在任何残差连接之前立即应用于DiT块中。
Transformer解码器输出噪声预测和输出对角协方差预测。

图19. 扩散Transformer（DiT）架构。
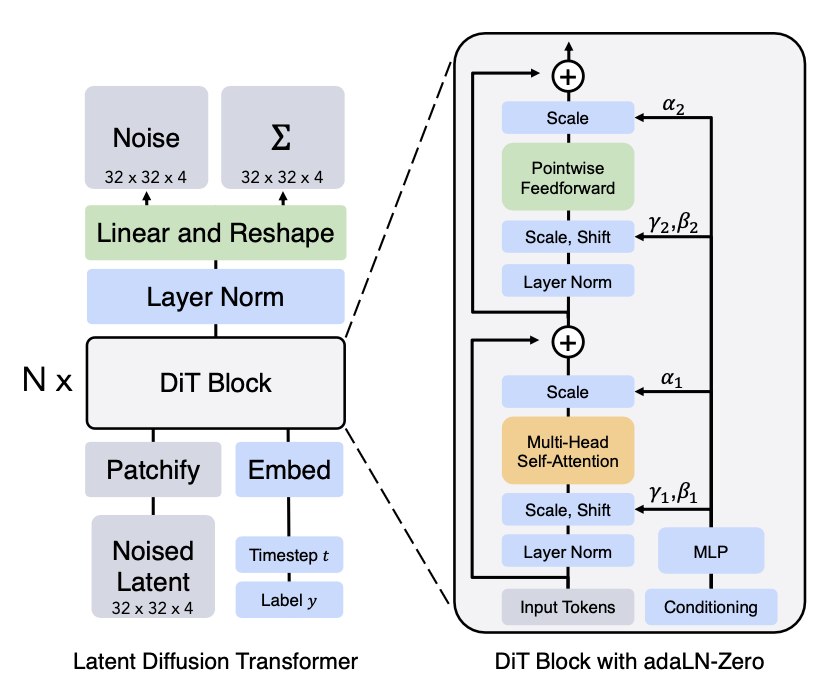
（图片来源：Peebles & Xie，2023）

Transformer架构可以轻松扩展，这是DiT的最大优点之一，因为其性能随着更多计算量的增加而提高，较大的DiT模型在实验中显示出更高的计算效率。

快速总结

优点：在生成建模中，可追溯性和灵活性是两个相互冲突的目标。可追溯的模型可以进行分析评估并廉价地拟合数据（例如通过高斯或拉普拉斯），但它们不能轻易描述丰富数据集中的结构。灵活的模型可以拟合数据中的任意结构，但评估、训练或从这些模型中采样通常非常昂贵。扩散模型既是可追溯的，又是灵活的。
缺点：扩散模型依赖于长的扩散步骤马尔可夫链生成样本，因此在时间和计算方面可能相当昂贵。已提出新的方法使这一过程更快，但采样仍然比GAN慢。

引用

引用为：

Weng, Lilian.（2021年7月）。什么是扩散模型？Lil’Log。https://lilianweng.github.io/posts/2021-07-11-diffusion-models/。

或者

@article{weng2021diffusion,
  title   = "What are diffusion models?",
  author  = "Weng, Lilian",
  journal = "lilianweng.github.io",
  year    = "2021",
  month   = "Jul",
  url     = "https://lilianweng.github.io/posts/2021-07-11-diffusion-models/"
}