生成扩散模型漫谈（四）：DDIM = 高观点DDPM

相信很多读者都听说过甚至读过克莱因的《高观点下的初等数学》这套书，顾名思义，这是在学到了更深入、更完备的数学知识后，从更高的视角重新审视过往学过的初等数学，以得到更全面的认知，甚至达到温故而知新的效果。类似的书籍还有很多，比如《重温微积分》、《复分析：可视化方法》等。

回到扩散模型，目前我们已经通过三篇文章从不同视角去解读了DDPM，那么它是否也存在一个更高的理解视角，让我们能从中得到新的收获呢？当然有，《Denoising Diffusion Implicit Models》介绍的DDIM模型就是经典的案例，本文一起来欣赏它。

思路分析 #

在《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》中，我们提到过该文章所介绍的推导跟DDIM紧密相关。具体来说，文章的推导路线可以简单归纳如下：
$$\begin{array}{}\text{(1)}& p({\mathit{x}}_t|{\mathit{x}}_{t-1})\stackrel{\text{推导}}{\to }p({\mathit{x}}_t|{\mathit{x}}_0)\stackrel{\text{推导}}{\to }p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)\stackrel{\text{近似}}{\to }p({\mathit{x}}_{t-1}|{\mathit{x}}_t)\end{array}$$
这个过程是一步步递进的。然而，我们发现最终结果有着两个特点：

1、损失函数只依赖于$p({\mathit{x}}_t|{\mathit{x}}_0)$；

2、采样过程只依赖于$p({\mathit{x}}_{t-1}|{\mathit{x}}_t)$。

也就是说，尽管整个过程是以$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$为出发点一步步往前推的，但是从结果上来看，压根儿就没$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$的事。那么，我们大胆地“异想天开”一下：

高观点1： 既然结果跟$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$无关，可不可以干脆“过河拆桥”，将$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$从整个推导过程中去掉？

DDIM正是这个“异想天开”的产物！

待定系数 #

可能有读者会想，根据上一篇文章所用的贝叶斯定理
$$\begin{array}{}\text{(2)}& p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)=\frac{p({\mathit{x}}_t|{\mathit{x}}_{t-1})p({\mathit{x}}_{t-1}|{\mathit{x}}_0)}{p({\mathit{x}}_t|{\mathit{x}}_0)}\end{array}$$
没有给定$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$怎么能得到$p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)$？这其实是思维过于定式了，理论上在没有给定$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$的情况下，$p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)$的解空间更大，某种意义上来说是更加容易推导，此时它只需要满足边际分布条件：
$$\begin{array}{}\text{(3)}& \int p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)p({\mathit{x}}_t|{\mathit{x}}_0)d{\mathit{x}}_t=p({\mathit{x}}_{t-1}|{\mathit{x}}_0)\end{array}$$
我们用待定系数法来求解这个方程。在上一篇文章中，所解出的$p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)$是一个正态分布，所以这一次我们可以更一般地设
$$\begin{array}{}\text{(4)}& p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)=\mathcal{N}({\mathit{x}}_{t-1};{\kappa }_t{\mathit{x}}_t+{\lambda }_t{\mathit{x}}_0,{\sigma }_t^2\mathit{I})\end{array}$$
其中${\kappa }_t,{\lambda }_t,{\sigma }_t$都是待定系数，而为了不重新训练模型，我们不改变$p({\mathit{x}}_{t-1}|{\mathit{x}}_0)$和$p({\mathit{x}}_t|{\mathit{x}}_0)$，于是我们可以列出
$$\overline{)\begin{array}{ccc}\text{记号}& \text{含义}& \text{采样}\\ p({\mathit{x}}_{t-1}|{\mathit{x}}_0)& \mathcal{N}({\mathit{x}}_{t-1};{\overline{\alpha }}_{t-1}{\mathit{x}}_0,{\overline{\beta }}_{t-1}^2\mathit{I})& {\mathit{x}}_{t-1}={\overline{\alpha }}_{t-1}{\mathit{x}}_0+{\overline{\beta }}_{t-1}\mathit{\epsilon }\\ p({\mathit{x}}_t|{\mathit{x}}_0)& \mathcal{N}({\mathit{x}}_t;{\overline{\alpha }}_t{\mathit{x}}_0,{\overline{\beta }}_t^2\mathit{I})& {\mathit{x}}_t={\overline{\alpha }}_t{\mathit{x}}_0+{\overline{\beta }}_t{\mathit{\epsilon }}_1\\ p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)& \mathcal{N}({\mathit{x}}_{t-1};{\kappa }_t{\mathit{x}}_t+{\lambda }_t{\mathit{x}}_0,{\sigma }_t^2\mathit{I})& {\mathit{x}}_{t-1}={\kappa }_t{\mathit{x}}_t+{\lambda }_t{\mathit{x}}_0+{\sigma }_t{\mathit{\epsilon }}_2\\ \begin{array}{c}\int p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)\\ p({\mathit{x}}_t|{\mathit{x}}_0)d{\mathit{x}}_t\end{array}& & \begin{array}{rl}{\mathit{x}}_{t-1}=& {\kappa }_t{\mathit{x}}_t+{\lambda }_t{\mathit{x}}_0+{\sigma }_t{\mathit{\epsilon }}_2\\ =& {\kappa }_t({\overline{\alpha }}_t{\mathit{x}}_0+{\overline{\beta }}_t{\mathit{\epsilon }}_1)+{\lambda }_t{\mathit{x}}_0+{\sigma }_t{\mathit{\epsilon }}_2\\ =& ({\kappa }_t{\overline{\alpha }}_t+{\lambda }_t){\mathit{x}}_0+({\kappa }_t{\overline{\beta }}_t{\mathit{\epsilon }}_1+{\sigma }_t{\mathit{\epsilon }}_2)\end{array}\end{array}}$$
其中$\mathit{\epsilon },{\mathit{\epsilon }}_1,{\mathit{\epsilon }}_2\sim \mathcal{N}(\mathbf{0},\mathit{I})$，并且由正态分布的叠加性我们知道${\kappa }_t{\overline{\beta }}_t{\mathit{\epsilon }}_1+{\sigma }_t{\mathit{\epsilon }}_2\sim \sqrt{{\kappa }_t^2{\overline{\beta }}_t^2+{\sigma }_t^2}\mathit{\epsilon }$。对比${\mathit{x}}_{t-1}$的两个采样形式，我们发现要想$\text{(3)}$成立，只需要满足两个方程
$$\begin{array}{}\text{(5)}& {\overline{\alpha }}_{t-1}={\kappa }_t{\overline{\alpha }}_t+{\lambda }_t,{\overline{\beta }}_{t-1}=\sqrt{{\kappa }_t^2{\overline{\beta }}_t^2+{\sigma }_t^2}\end{array}$$
可以看到有三个未知数，但只有两个方程，这就是为什么说没有给定$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$时解空间反而更大了。将${\sigma }_t$视为可变参数，可以解出
$$\begin{array}{}\text{(6)}& {\kappa }_t=\frac{\sqrt{{\overline{\beta }}_{t-1}^2-{\sigma }_t^2}}{{\overline{\beta }}_t},{\lambda }_t={\overline{\alpha }}_{t-1}-\frac{{\overline{\alpha }}_t\sqrt{{\overline{\beta }}_{t-1}^2-{\sigma }_t^2}}{{\overline{\beta }}_t}\end{array}$$
或者写成
$$\begin{array}{}\text{(7)}& p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)=\mathcal{N}({\mathit{x}}_{t-1};\frac{\sqrt{{\overline{\beta }}_{t-1}^2-{\sigma }_t^2}}{{\overline{\beta }}_t}{\mathit{x}}_t+({\overline{\alpha }}_{t-1}-\frac{{\overline{\alpha }}_t\sqrt{{\overline{\beta }}_{t-1}^2-{\sigma }_t^2}}{{\overline{\beta }}_t}){\mathit{x}}_0,{\sigma }_t^2\mathit{I})\end{array}$$
方便起见，我们约定${\overline{\alpha }}_0=1,{\overline{\beta }}_0=0$。特别地，这个结果并不需要限定${\overline{\alpha }}_t^2+{\overline{\beta }}_t^2=1$，不过为了简化参数设置，同时也为了跟以往的结果对齐，这里还是约定${\overline{\alpha }}_t^2+{\overline{\beta }}_t^2=1$。

一如既往 #

现在我们在只给定$p({\mathit{x}}_t|{\mathit{x}}_0)$、$p({\mathit{x}}_{t-1}|{\mathit{x}}_0)$的情况下，通过待定系数法求解了$p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)$的一簇解，它带有一个自由参数${\sigma }_t$。用《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》中的“拆楼-建楼”类比来说，就是我们知道楼会被拆成什么样【$p({\mathit{x}}_t|{\mathit{x}}_0)$、$p({\mathit{x}}_{t-1}|{\mathit{x}}_0)$】，但是不知道每一步怎么拆【$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$】，然后希望能够从中学会每一步怎么建【$p({\mathit{x}}_{t-1}|{\mathit{x}}_t)$】。当然，如果我们想看看每一步怎么拆的话，也可以反过来用贝叶斯公式
$$\begin{array}{}\text{(8)}& p({\mathit{x}}_t|{\mathit{x}}_{t-1},{\mathit{x}}_0)=\frac{p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)p({\mathit{x}}_t|{\mathit{x}}_0)}{p({\mathit{x}}_{t-1}|{\mathit{x}}_0)}\end{array}$$

接下来的事情，就跟上一篇文章一模一样了：我们最终想要$p({\mathit{x}}_{t-1}|{\mathit{x}}_t)$而不是$p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0)$，所以我们希望用
$$\begin{array}{}\text{(9)}& \overline{\mathit{\mu }}({\mathit{x}}_t)=\frac{1}{{\overline{\alpha }}_t}({\mathit{x}}_t-{\overline{\beta }}_t{\mathit{ϵ}}_{\mathit{\theta }}({\mathit{x}}_t,t))\end{array}$$
来估计${\mathit{x}}_0$，由于没有改动$p({\mathit{x}}_t|{\mathit{x}}_0)$，所以训练所用的目标函数依然是${\Vert \mathit{\epsilon }-{\mathit{ϵ}}_{\mathit{\theta }}({\overline{\alpha }}_t{\mathit{x}}_0+{\overline{\beta }}_t\mathit{\epsilon },t)\Vert }^2$（除去权重系数），也就是说训练过程没有改变，我们可以用回DDPM训练好的模型。而用$\overline{\mathit{\mu }}({\mathit{x}}_t)$替换掉式$\text{(7)}$中的${\mathit{x}}_0$后，得到
$$\begin{array}{}\text{(10)}& \begin{array}{rl}p({\mathit{x}}_{t-1}|{\mathit{x}}_t)\approx & p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0=\overline{\mathit{\mu }}({\mathit{x}}_t))\\ =& \mathcal{N}({\mathit{x}}_{t-1};\frac{1}{{\alpha }_t}({\mathit{x}}_t-({\overline{\beta }}_t-{\alpha }_t\sqrt{{\overline{\beta }}_{t-1}^2-{\sigma }_t^2}){\mathit{ϵ}}_{\mathit{\theta }}({\mathit{x}}_t,t)),{\sigma }_t^2\mathit{I})\end{array}\end{array}$$
这就求出了生成过程所需要的$p({\mathit{x}}_{t-1}|{\mathit{x}}_t)$，其中${\alpha }_t=\frac{{\overline{\alpha }}_t}{{\overline{\alpha }}_{t-1}}$。它的特点是训练过程没有变化（也就是说最终保存下来的模型没有变化），但生成过程却有一个可变动的参数${\sigma }_t$，就是这个参数给DDPM带来了新鲜的结果。

几个例子 #

原则上来说，我们对${\sigma }_t$没有过多的约束，但是不同${\sigma }_t$的采样过程会呈现出不同的特点，我们举几个例子进行分析。

第一个简单例子就是取${\sigma }_t=\frac{{\overline{\beta }}_{t-1}{\beta }_t}{{\overline{\beta }}_t}$，其中${\beta }_t=\sqrt{1-{\alpha }_t^2}$，相应地有
$$\begin{array}{}\text{(11)}& p({\mathit{x}}_{t-1}|{\mathit{x}}_t)\approx p({\mathit{x}}_{t-1}|{\mathit{x}}_t,{\mathit{x}}_0=\overline{\mathit{\mu }}({\mathit{x}}_t))=\mathcal{N}({\mathit{x}}_{t-1};\frac{1}{{\alpha }_t}({\mathit{x}}_t-\frac{{\beta }_t^2}{{\overline{\beta }}_t}{\mathit{ϵ}}_{\mathit{\theta }}({\mathit{x}}_t,t)),\frac{{\overline{\beta }}_{t-1}^2{\beta }_t^2}{{\overline{\beta }}_t^2}\mathit{I})\end{array}$$
这就是上一篇文章所推导的DDPM。特别是，DDIM论文中还对${\sigma }_t=\eta \frac{{\overline{\beta }}_{t-1}{\beta }_t}{{\overline{\beta }}_t}$做了对比实验，其中$\eta \in [0,1]$。

第二个例子就是取${\sigma }_t={\beta }_t$，这也是前两篇文章所指出的${\sigma }_t$的两个选择之一，在此选择下式$\text{(10)}$未能做进一步的化简，但DDIM的实验结果显示此选择在DDPM的标准参数设置下表现还是很好的。

最特殊的一个例子是取${\sigma }_t=0$，此时从${\mathit{x}}_t$到${\mathit{x}}_{t-1}$是一个确定性变换
$$\begin{array}{}\text{(12)}& {\mathit{x}}_{t-1}=\frac{1}{{\alpha }_t}({\mathit{x}}_t-({\overline{\beta }}_t-{\alpha }_t{\overline{\beta }}_{t-1}){\mathit{ϵ}}_{\mathit{\theta }}({\mathit{x}}_t,t))\end{array}$$
这也是DDIM论文中特别关心的一个例子，准确来说，原论文的DDIM就是特指${\sigma }_t=0$的情形，其中“I”的含义就是“Implicit”，意思这是一个隐式的概率模型，因为跟其他选择所不同的是，此时从给定的${\mathit{x}}_T=\mathit{z}$出发，得到的生成结果${\mathit{x}}_0$是不带随机性的。后面我们将会看到，这在理论上和实用上都带来了一些好处。

加速生成 #

值得指出的是，在这篇文章中我们没有以$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$为出发点，所以前面的所有结果实际上全都是以${\overline{\alpha }}_t,{\overline{\beta }}_t$相关记号给出的，而${\alpha }_t,{\beta }_t$则是通过${\alpha }_t=\frac{{\overline{\alpha }}_t}{{\overline{\alpha }}_{t-1}}$和${\beta }_t=\sqrt{1-{\alpha }_t^2}$派生出来的记号。从损失函数${\Vert \mathit{\epsilon }-{\mathit{ϵ}}_{\mathit{\theta }}({\overline{\alpha }}_t{\mathit{x}}_0+{\overline{\beta }}_t\mathit{\epsilon },t)\Vert }^2$可以看出，给定了各个${\overline{\alpha }}_t$，训练过程也就确定了。

从这个过程中，DDIM进一步留意到了如下事实：

高观点2： DDPM的训练结果实质上包含了它的任意子序列参数的训练结果。

具体来说，设$\mathit{\tau }=[{\tau }_1,{\tau }_2,\dots ,{\tau }_{\dim (\mathit{\tau })}]$是$[1,2,\cdots ,T]$的任意子序列，那么我们以${\overline{\alpha }}_{{\tau }_1},{\overline{\alpha }}_{{\tau }_2},\cdots ,{\overline{\alpha }}_{\dim (\mathit{\tau })}$为参数训练一个扩散步数为$\dim (\mathit{\tau })$步的DDPM，其目标函数实际上是原来以${\overline{\alpha }}_1,{\overline{\alpha }}_2,\cdots ,{\overline{\alpha }}_T$的$T$步DDPM的目标函数的一个子集！所以在模型拟合能力足够好的情况下，它其实包含了任意子序列参数的训练结果。

那么反过来想，如果有一个训练好的$T$步DDPM模型，我们也可以将它当成是以${\overline{\alpha }}_{{\tau }_1},{\overline{\alpha }}_{{\tau }_2},\cdots ,{\overline{\alpha }}_{\dim (\mathit{\tau })}$为参数训练出来的$\dim (\mathit{\tau })$步模型，而既然是$\dim (\mathit{\tau })$步的模型，生成过程也就只需要$\dim (\mathit{\tau })$步了，根据式$\text{(10)}$有：
$$\begin{array}{}\text{(13)}& p({\mathit{x}}_{{\tau }_{i-1}}|{\mathit{x}}_{{\tau }_i})\approx \mathcal{N}({\mathit{x}}_{{\tau }_{i-1}};\frac{{\overline{\alpha }}_{{\tau }_{i-1}}}{{\overline{\alpha }}_{{\tau }_i}}({\mathit{x}}_{{\tau }_i}-({\overline{\beta }}_{{\tau }_i}-\frac{{\overline{\alpha }}_{{\tau }_i}}{{\overline{\alpha }}_{{\tau }_{i-1}}}\sqrt{{\overline{\beta }}_{{\tau }_{i-1}}^2-{\tilde{\sigma }}_{{\tau }_i}^2}){\mathit{ϵ}}_{\mathit{\theta }}({\mathit{x}}_{{\tau }_i},{\tau }_i)),{\tilde{\sigma }}_{{\tau }_i}^2\mathit{I})\end{array}$$
这就是加速采样的生成过程了，从原来的$T$步扩散生成变成了$\dim (\mathit{\tau })$步。要注意不能直接将式$\text{(10)}$的${\alpha }_t$换成${\alpha }_{{\tau }_i}$，因为我们说过${\alpha }_t$是派生记号而已，它实际上等于$\frac{{\overline{\alpha }}_t}{{\overline{\alpha }}_{t-1}}$，因此${\alpha }_t$要换成$\frac{{\overline{\alpha }}_{{\tau }_i}}{{\overline{\alpha }}_{{\tau }_{i-1}}}$才对。同理，${\tilde{\sigma }}_{{\tau }_i}$也不是直接取${\sigma }_{{\tau }_i}$，而是在将其定义全部转化为$\overline{\alpha },\overline{\beta }$符号后，将$t$替换为${\tau }_i$、$t-1$替换为${\tau }_{i-1}$，比如式$\text{(11)}$对应的${\tilde{\sigma }}_{{\tau }_i}$为
$$\begin{array}{}\text{(14)}& {\sigma }_t=\frac{{\overline{\beta }}_{t-1}{\beta }_t}{{\overline{\beta }}_t}=\frac{{\overline{\beta }}_{t-1}}{{\overline{\beta }}_t}\sqrt{1-\frac{{\overline{\alpha }}_t^2}{{\overline{\alpha }}_{t-1}^2}}\to \frac{{\overline{\beta }}_{{\tau }_{i-1}}}{{\overline{\beta }}_{{\tau }_i}}\sqrt{1-\frac{{\overline{\alpha }}_{{\tau }_i}^2}{{\overline{\alpha }}_{{\tau }_{i-1}}^2}}={\tilde{\sigma }}_{{\tau }_i}\end{array}$$

可能读者又想问，我们为什么干脆不直接训练一个$\dim (\mathit{\tau })$步的扩散模型，而是要先训练$T>\dim (\mathit{\tau })$步然后去做子序列采样？笔者认为可能有两方面的考虑：一方面从$\dim (\mathit{\tau })$步生成来说，训练更多步数的模型也许能增强泛化能力；另一方面，通过子序列$\mathit{\tau }$进行加速只是其中一种加速手段，训练更充分的$T$步允许我们尝试更多的其他加速手段，但并不会显著增加训练成本。

实验结果 #

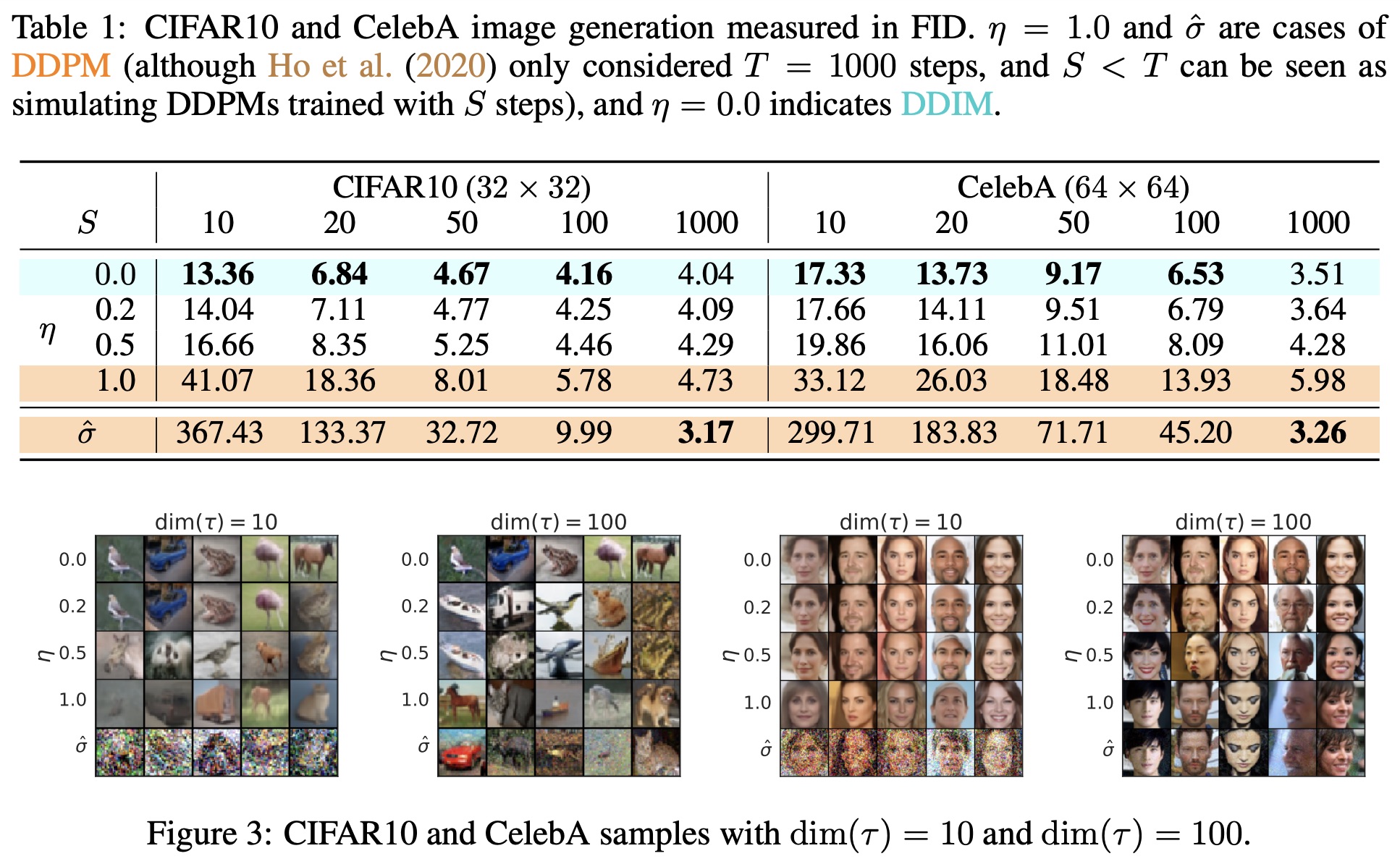
原论文对不同的噪声强度和扩散步数$\dim (\mathit{\tau })$做了组合对比，大致上的结果是“噪声越小，加速后的生成效果越好”，如下图

DDIM的实验结果，显示噪声越小，加速后的生成效果越好

 

笔者的参考实现如下：

Github：https://github.com/bojone/Keras-DDPM/blob/main/ddim.py

个人的实验结论是：

1、可能跟直觉相反，生成过程中的${\sigma }_t$越小，最终生成图像的噪声和多样性反而相对来说越大；

2、扩散步数$\dim (\mathit{\tau })$越少，生成的图片更加平滑，多样性也会有所降低；

3、结合1、2两点得知，在扩散步数$\dim (\mathit{\tau })$减少时，可以适当缩小${\sigma }_t$，以保持生成图片质量大致不变，这跟DDIM原论文的实验结论是一致的；

4、在${\sigma }_t$较小时，相比可训练的Embedding层，用固定的Sinusoidal编码来表示$t$所生成图片的噪声要更小；

5、在${\sigma }_t$较小时，原论文的U-Net架构（Github中的ddpm2.py）要比笔者自行构思的U-Net架构（Github中的ddpm.py）所生成图片的噪声要更小；

6、但个人感觉，总体来说不带噪声的生成过程的生成效果不如带噪声的生成过程，不带噪声时生成效果受模型架构影响较大。

此外，对于${\sigma }_t=0$时的DDIM，它就是将任意正态噪声向量变换为图片的一个确定性变换，这已经跟GAN几乎一致了，所以跟GAN类似，我们可以对噪声向量进行插值，然后观察对应的生成效果。但要注意的是，DDPM或DDIM对噪声分布都比较敏感，所以我们不能用线性插值而要用球面插值，因为由正态分布的叠加性，如果${\mathit{z}}_1,{\mathit{z}}_2\sim \mathcal{N}(\mathbf{0},\mathit{I})$，$\lambda {\mathit{z}}_1+(1-\lambda ){\mathit{z}}_2$一般就不服从$\mathcal{N}(\mathbf{0},\mathit{I})$，要改为
$$\begin{array}{}\text{(15)}& \mathit{z}={\mathit{z}}_1\cos \frac{\lambda \pi }{2}+{\mathit{z}}_2\sin \frac{\lambda \pi }{2},\lambda \in [0,1]\end{array}$$

插值效果演示（笔者自己训练的模型）：

DDIM随机向量的插值生成效果

 

微分方程 #

最后，我们来重点分析一下${\sigma }_t=0$的情形。此时$\text{(12)}$可以等价地改写成：
$$\begin{array}{}\text{(16)}& \frac{{\mathit{x}}_t}{{\overline{\alpha }}_t}-\frac{{\mathit{x}}_{t-1}}{{\overline{\alpha }}_{t-1}}=(\frac{{\overline{\beta }}_t}{{\overline{\alpha }}_t}-\frac{{\overline{\beta }}_{t-1}}{{\overline{\alpha }}_{t-1}}){\mathit{ϵ}}_{\mathit{\theta }}({\mathit{x}}_t,t)\end{array}$$
当$T$足够大，或者说${\alpha }_t$与${\alpha }_{t-1}$足够小时，我们可以将上式视为某个常微分方程的差分形式。特别地，引入虚拟的时间参数$s$，我们得到
$$\begin{array}{}\text{(17)}& \frac{d}{ds}\left(\frac{\mathit{x}(s)}{\overline{\alpha }(s)}\right)={\mathit{ϵ}}_{\mathit{\theta }}(\mathit{x}(s),t(s))\frac{d}{ds}\left(\frac{\overline{\beta }(s)}{\overline{\alpha }(s)}\right)\end{array}$$
不失一般性，假设$s\in [0,1]$，其中$s=0$对应$t=0$、$s=1$对应$t=T$。注意DDIM原论文直接用$\frac{\overline{\beta }(s)}{\overline{\alpha }(s)}$作为虚拟时间参数，这原则上是不大适合的，因为它的范围是$[0,\mathrm{\infty })$，无界的区间不利于数值求解。

那么现在我们要做的事情就是在给定$\mathit{x}(1)\sim \mathcal{N}(\mathbf{0},\mathit{I})$的情况下，去求解出$\mathit{x}(0)$。而DDPM或者DDIM的迭代过程，对应于该常微分方程的欧拉方法。众所周知欧拉法的效率相对来说是最慢的，如果要想加速求解，可以用Heun方法、R-K方法等。也就是说，将生成过程等同于求解常微分方程后，可以借助常微分方程的数值解法，为生成过程的加速提供更丰富多样的手段。

以DDPM的默认参数$T=1000$、${\alpha }_t=\sqrt{1-\frac{0.02t}{T}}$为例，我们重复《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》所做的估计
$$\begin{array}{}\text{(18)}& \log {\overline{\alpha }}_t=\sum _{i=k}^t\log {\alpha }_k=\frac{1}{2}\sum _{k=1}^t\log (1-\frac{0.02k}{T})<\frac{1}{2}\sum _{k=1}^t(-\frac{0.02k}{T})=-\frac{0.005t(t+1)}{T}\end{array}$$
事实上，由于每个${\alpha }_k$都很接近于1，所以上述估计其实也是一个很好的近似。而我们说了本文的出发点是$p({\mathit{x}}_t|{\mathit{x}}_0)$，所以应该以${\overline{\alpha }}_t$为起点，根据上述近似，我们可以直接简单地取
$$\begin{array}{}\text{(19)}& {\overline{\alpha }}_t=\exp (-\frac{0.005t^2}{T})=\exp (-\frac{5t^2}{T^2})\end{array}$$
如果取$s=t/T$为参数，那么正好$s\in [0,1]$，此时$\overline{\alpha }(s)=e^{-5s^2}$，代入到式$\text{(17)}$化简得
$$\begin{array}{}\text{(20)}& \frac{d\mathit{x}(s)}{ds}=10s(\frac{{\mathit{ϵ}}_{\mathit{\theta }}(\mathit{x}(s),sT)}{\sqrt{1-e^{-10s^2}}}-\mathit{x}(s))\end{array}$$
也可以取$s=t^2/T^2$为参数，此时也有$s\in [0,1]$，以及$\overline{\alpha }(s)=e^{-5s}$，代入到式$\text{(17)}$化简得
$$\begin{array}{}\text{(21)}& \frac{d\mathit{x}(s)}{ds}=5(\frac{{\mathit{ϵ}}_{\mathit{\theta }}(\mathit{x}(s),\sqrt{s}T)}{\sqrt{1-e^{-10s}}}-\mathit{x}(s))\end{array}$$

文章小结 #

本文接着上一篇DDPM的推导思路来介绍了DDIM，它重新审视了DDPM的出发点，去掉了推导过程中的$p({\mathit{x}}_t|{\mathit{x}}_{t-1})$，从而获得了一簇更广泛的解和加速生成过程的思路，最后这簇新解还允许我们将生成过程跟常微分方程的求解联系起来，从而借助常微分方程的方法进一步对生成过程进行研究。

转载到请包括本文地址：https://spaces.ac.cn/archives/9181

更详细的转载事宜请参考：《科学空间FAQ》