生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪
到目前为止,笔者给出了生成扩散模型DDPM的两种推导,分别是《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中的通俗类比方案和《生成扩散模型漫谈(二):DDPM = 自回归式VAE》中的变分自编码器方案。两种方案可谓各有特点,前者更为直白易懂,但无法做更多的理论延伸和定量理解,后者理论分析上更加完备一些,但稍显形式化,启发性不足。
在这篇文章中,我们再分享DDPM的一种推导,它主要利用到了贝叶斯定理来简化计算,整个过程的“推敲”味道颇浓,很有启发性。不仅如此,它还跟我们后面将要介绍的DDIM模型有着紧密的联系。
模型绘景 #
再次回顾,DDPM建模的是如下变换流程:
其中,正向就是将样本数据
正向过程很简单,每一步是
或者写成
从而可以求出
DDPM要做的事情,就是从上述信息中求出反向过程所需要的
请贝叶斯 #
下面我们请出伟大的贝叶斯定理。事实上,直接根据贝叶斯定理我们有
然而,我们并不知道
这样修改自然是因为
推导:上式的推导过程并不难,就是常规的展开整理而已,当然我们也可以找点技巧加快计算。首先,代入各自的表达式,可以发现指数部分除掉因子外,结果是:
它关于是二次的,因此最终的分布必然也是正态分布,我们只需要求出其均值和协方差。不难看出,展开式中 项的系数是
所以整理好的结果必然是的形式,这意味着协方差矩阵是 。另一边,把一次项系数拿出来是 ,除以 后便可以得到
这就得到了的所有信息了,结果正是式 。
去噪过程 #
现在我们得到了
如果我们能够通过来预测 ,那么不就可以消去 中的 ,使得它只依赖于 了吗?
说干就干,我们用
在
具体来说,
此时损失函数变为
省去前面的系数,就得到DDPM原论文所用的损失函数了。可以发现,本文是直接得出了从
另一边,我们将式
这就是反向的采样过程所用的分布,连同采样过程所用的方差也一并确定下来了。至此,DDPM推导完毕~(提示:出于推导的流畅性考虑,本文的
推导:将式代入到式 的主要化简难度就是计算
预估修正 #
不知道读者有没有留意到一个有趣的地方:我们要做的事情,就是想将
真实情况是,“用
由此我们还可以联想到Hinton三年前提出的《Lookahead Optimizer: k steps forward, 1 step back》,它同样也包含了预估(k steps forward)和修正(1 step back)两部分,原论文将其诠释为“快(Fast)-慢(Slow)”权重的相互结合,快权重就是预估得到的结果,慢权重则是基于预估所做的修正结果。如果愿意,我们也可以用同样的方式去诠释DDPM的“预估-修正”过程~
遗留问题 #
最后,在使用贝叶斯定理一节中,我们说式
其中
第一个例子是整个数据集只有一个样本,不失一般性,假设该样本为
我们主要关心其方差为
第二个例子是数据集服从标准正态分布,即
跟推导
我们同样主要关心其方差为
文章小结 #
本文分享了DDPM的一种颇有“推敲”味道的推导,它借助贝叶斯定理来直接推导反向的生成过程,相比之前的“拆楼-建楼”类比和变分推断理解更加一步到位。同时,它也更具启发性,跟接下来要介绍的DDIM有很密切的联系。
转载到请包括本文地址:https://spaces.ac.cn/archives/9164
更详细的转载事宜请参考:《科学空间FAQ》


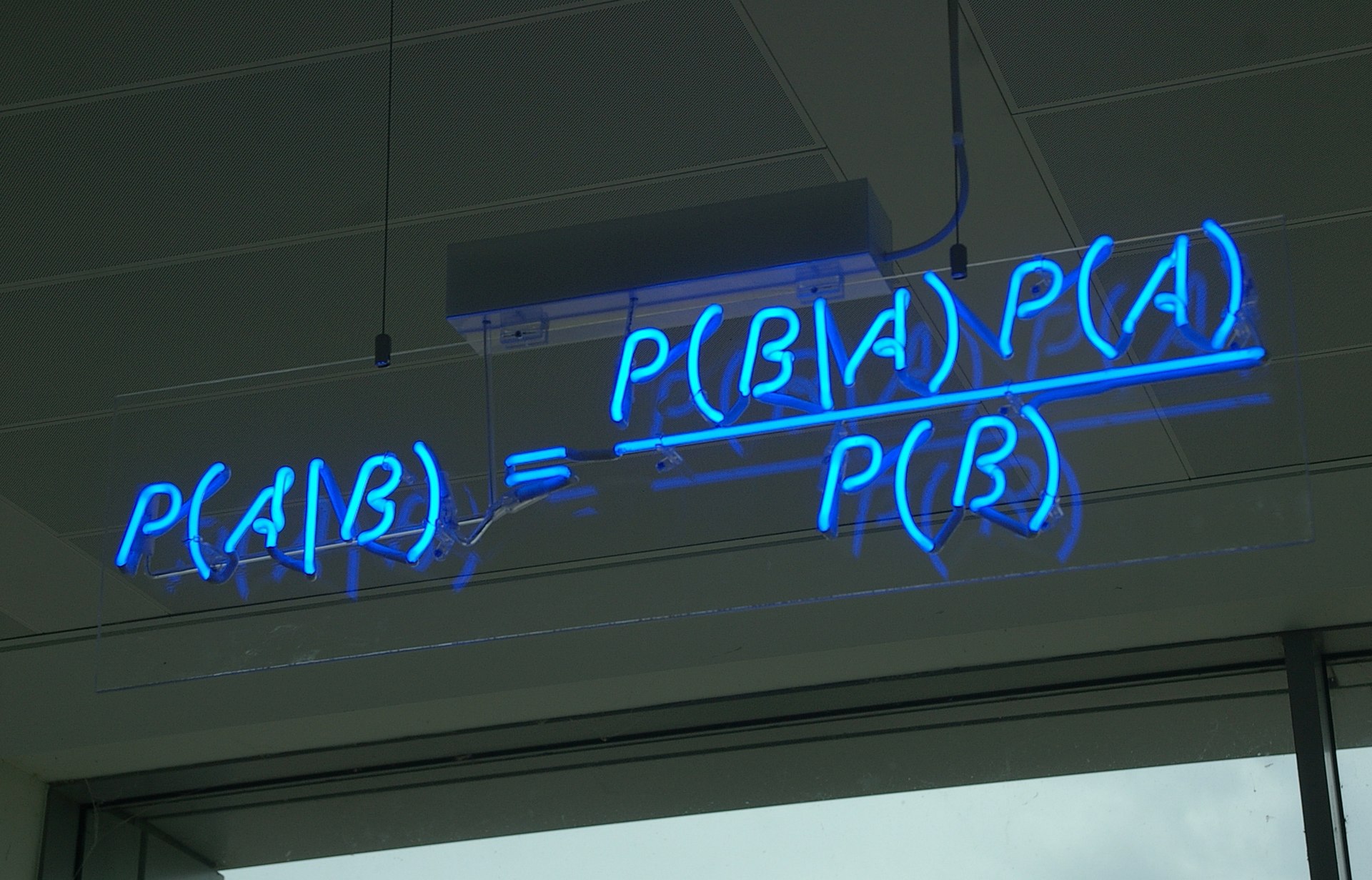


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧