变分自编码器（五）：VAE + BN = 更好的VAE

本文我们继续之前的变分自编码器系列，分析一下如何防止NLP中的VAE模型出现“KL散度消失（KL Vanishing）”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发，并自行做了进一步的完善。

值得一提的是，本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN（Batch Normalization），然后加个简单的scale——但确实很有效，因此值得正在研究相关问题的读者一试。同时，相关结论也适用于一般的VAE模型（包括CV的），如果按照笔者的看法，它甚至可以作为VAE模型的“标配”。

最后，要提醒读者这算是一篇VAE的进阶论文，所以请读者对VAE有一定了解后再来阅读本文。

VAE简单回顾 #

这里我们简单回顾一下VAE模型，并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍，请读者参考笔者的旧作《变分自编码器（一）：原来是这么一回事》、《变分自编码器（二）：从贝叶斯观点出发》等。

VAE的训练流程 #

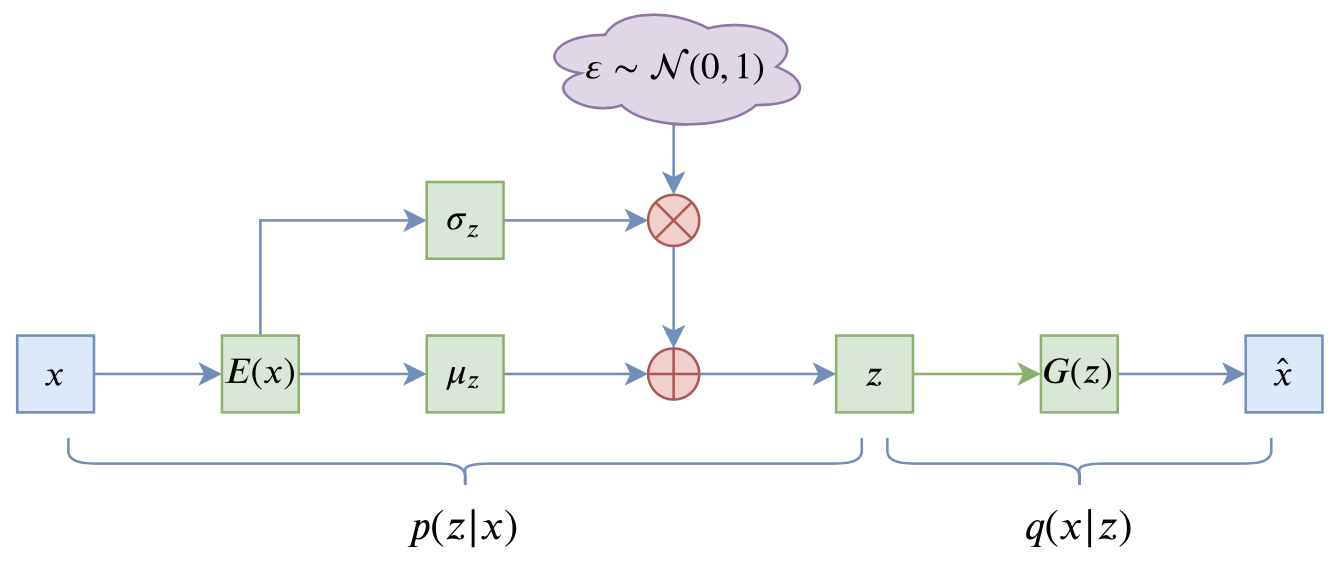
VAE的训练流程大概可以图示为

VAE训练流程图示

 

写成公式就是
$$\begin{array}{}\text{(1)}& \mathcal{L}={\mathbb{E}}_{x\sim \tilde{p}(x)}[{\mathbb{E}}_{z\sim p(z|x)}[-\log q(x|z)]+KL(p(z|x)\Vert q(z))]\end{array}$$
其中第一项就是重构项，${\mathbb{E}}_{z\sim p(z|x)}$是通过重参数来实现；第二项则称为KL散度项，这是它跟普通自编码器的显式差别，如果没有这一项，那么基本上退化为常规的AE。更详细的符号含义可以参考《变分自编码器（二）：从贝叶斯观点出发》。

NLP中的VAE #

在NLP中，句子被编码为离散的整数ID，所以$q(x|z)$是一个离散型分布，可以用万能的“条件语言模型”来实现，因此理论上$q(x|z)$可以精确地拟合生成分布，问题就出在$q(x|z)$太强了，训练时重参数操作会来噪声，噪声一大，$z$的利用就变得困难起来，所以它干脆不要$z$了，退化为无条件语言模型（依然很强），$KL(p(z|x)\Vert q(z))$则随之下降到0，这就出现了KL散度消失现象。

这种情况下的VAE模型并没有什么价值：KL散度为0说明编码器输出的是常数向量，而解码器则是一个普通的语言模型。而我们使用VAE通常来说是看中了它无监督构建编码向量的能力，所以要应用VAE的话还是得解决KL散度消失问题。事实上从2016开始，有不少工作在做这个问题，相应地也提出了很多方案，比如退火策略、更换先验分布等，读者Google一下“KL Vanishing”就可以找到很多文献了，这里不一一溯源。

BN的巧与妙 #

本文的方案则是直接针对KL散度项入手，简单有效而且没什么超参数。其思想很简单：

KL散度消失不就是KL散度项变成0吗？我调整一下编码器输出，让KL散度有一个大于零的下界，这样它不就肯定不会消失了吗？

这个简单的思想的直接结果就是：在$\mu$后面加入BN层，如图

往VAE里加入BN

 

推导过程简述 #

为什么会跟BN联系起来呢？我们来看KL散度项的形式：
$$\begin{array}{}\text{(2)}& {\mathbb{E}}_{x\sim \tilde{p}(x)}[KL(p(z|x)\Vert q(z))]=\frac{1}{b}\sum _{i=1}^b\sum _{j=1}^d\frac{1}{2}({\mu }_{i,j}^2+{\sigma }_{i,j}^2-\log {\sigma }_{i,j}^2-1)\end{array}$$
上式是采样了$b$个样本进行计算的结果，而编码向量的维度则是$d$维。由于我们总是有$e^x\ge x+1$，所以${\sigma }_{i,j}^2-\log {\sigma }_{i,j}^2-1\ge 0$，因此
$$\begin{array}{}\text{(3)}& {\mathbb{E}}_{x\sim \tilde{p}(x)}[KL(p(z|x)\Vert q(z))]\ge \frac{1}{b}\sum _{i=1}^b\sum _{j=1}^d\frac{1}{2}{\mu }_{i,j}^2=\frac{1}{2}\sum _{j=1}^d\left(\frac{1}{b}\sum _{i=1}^b{\mu }_{i,j}^2\right)\end{array}$$
留意到括号里边的量，其实它就是$\mu$在batch内的二阶矩，如果我们往$\mu$加入BN层，那么大体上可以保证$\mu$的均值为$\beta$，方差为${\gamma }^2$（$\beta ,\gamma$是BN里边的可训练参数），这时候
$$\begin{array}{}\text{(4)}& {\mathbb{E}}_{x\sim \tilde{p}(x)}[KL(p(z|x)\Vert q(z))]\ge \frac{d}{2}({\beta }^2+{\gamma }^2)\end{array}$$
所以只要控制好$\beta ,\gamma$（主要是固定$\gamma$为某个常数），就可以让KL散度项有个正的下界，因此就不会出现KL散度消失现象了。这样一来，KL散度消失现象跟BN就被巧妙地联系起来了，通过BN来“杜绝”了KL散度消失的可能性。

为什么不是LN？ #

善于推导的读者可能会想到，按照上述思路，如果只是为了让KL散度项有个正的下界，其实LN（Layer Normalization）也可以，也就是在式$\text{(3)}$中按$j$那一维归一化。

那为什么用BN而不是LN呢？

这个问题的答案也是BN的巧妙之处。直观来理解，KL散度消失是因为$z\sim p(z|x)$的噪声比较大，解码器无法很好地辨别出$z$中的非噪声成分，所以干脆弃之不用；而当给$\mu (x)$加上BN后，相当于适当地拉开了不同样本的$z$的距离，使得哪怕$z$带了噪声，区分起来也容易一些，所以这时候解码器乐意用$z$的信息，因此能缓解这个问题；相比之下，LN是在样本内进的行归一化，没有拉开样本间差距的作用，所以LN的效果不会有BN那么好。

进一步的结果 #

事实上，原论文的推导到上面基本上就结束了，剩下的都是实验部分，包括通过实验来确定$\gamma$的值。然而，笔者认为目前为止的结论还有一些美中不足的地方，比如没有提供关于加入BN的更深刻理解，倒更像是一个工程的技巧，又比如只是$\mu (x)$加上了BN，$\sigma (x)$没有加上，未免有些不对称之感。

经过笔者的推导，发现上面的结论可以进一步完善。

联系到先验分布 #

对于VAE来说，它希望训练好后的模型的隐变量分布为先验分布$q(z)=\mathcal{N}(z;0,1)$，而后验分布则是$p(z|x)=\mathcal{N}(z;\mu (x),{\sigma }^2(x))$，所以VAE希望下式成立：
$$\begin{array}{}\text{(5)}& q(z)=\int \tilde{p}(x)p(z|x)dx=\int \tilde{p}(x)\mathcal{N}(z;\mu (x),{\sigma }^2(x))dx\end{array}$$
两边乘以$z$，并对$z$积分，得到
$$\begin{array}{}\text{(6)}& 0=\int \tilde{p}(x)\mu (x)dx={\mathbb{E}}_{x\sim \tilde{p}(x)}[\mu (x)]\end{array}$$
两边乘以$z^2$，并对$z$积分，得到
$$\begin{array}{}\text{(7)}& 1=\int \tilde{p}(x)[{\mu }^2(x)+{\sigma }^2(x)]dx={\mathbb{E}}_{x\sim \tilde{p}(x)}[{\mu }^2(x)]+{\mathbb{E}}_{x\sim \tilde{p}(x)}[{\sigma }^2(x)]\end{array}$$
如果往$\mu (x),\sigma (x)$都加入BN，那么我们就有
$$\begin{array}{}\text{(8)}& \begin{array}{rl}& 0={\mathbb{E}}_{x\sim \tilde{p}(x)}[\mu (x)]={\beta }_{\mu }\\ & 1={\mathbb{E}}_{x\sim \tilde{p}(x)}[{\mu }^2(x)]+{\mathbb{E}}_{x\sim \tilde{p}(x)}[{\sigma }^2(x)]={\beta }_{\mu }^2+{\gamma }_{\mu }^2+{\beta }_{\sigma }^2+{\gamma }_{\sigma }^2\end{array}\end{array}$$
所以现在我们知道${\beta }_{\mu }$一定是0，而如果我们也固定${\beta }_{\sigma }=0$，那么我们就有约束关系：
$$\begin{array}{}\text{(9)}& 1={\gamma }_{\mu }^2+{\gamma }_{\sigma }^2\end{array}$$

参考的实现方案 #

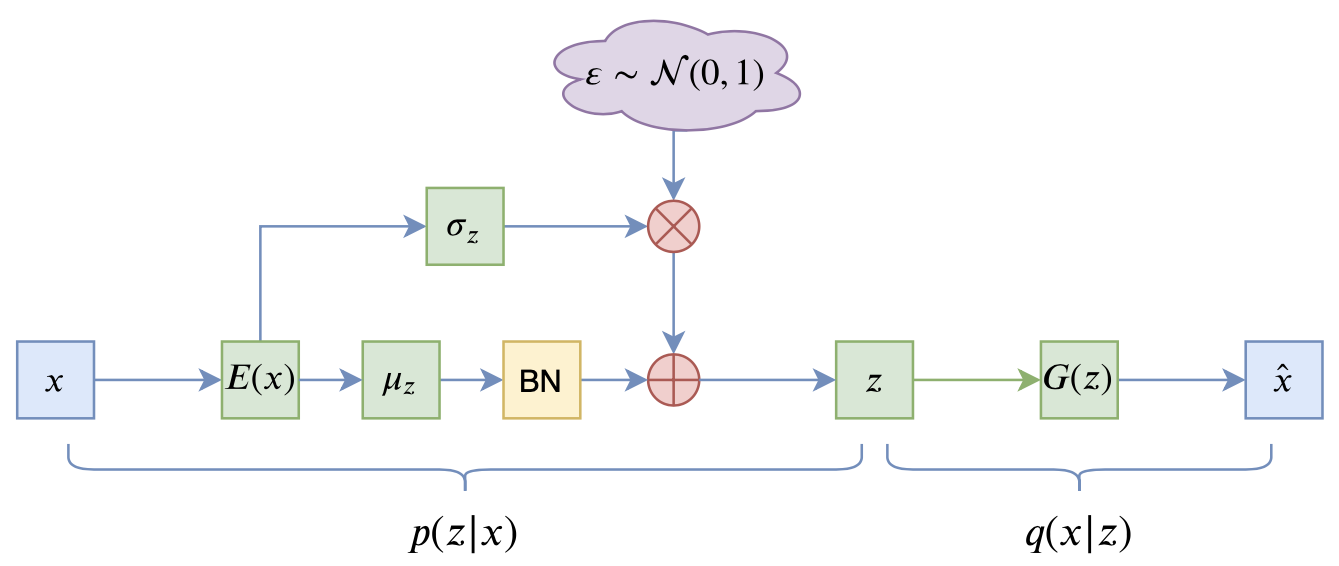
经过这样的推导，我们发现可以往$\mu (x),\sigma (x)$都加入BN，并且可以固定${\beta }_{\mu }={\beta }_{\sigma }=0$，但此时需要满足约束$\text{(9)}$。要注意的是，这部分讨论还仅仅是对VAE的一般分析，并没有涉及到KL散度消失问题，哪怕这些条件都满足了，也无法保证KL项不趋于0。结合式$\text{(4)}$我们可以知道，保证KL散度不消失的关键是确保${\gamma }_{\mu }>0$，所以，笔者提出的最终策略是：
$$\begin{array}{}\text{(10)}& \begin{array}{rl}& {\beta }_{\mu }={\beta }_{\sigma }=0\\ & {\gamma }_{\mu }=\sqrt{\tau +(1-\tau )\cdot \text{sigmoid}(\theta )}\\ & {\gamma }_{\sigma }=\sqrt{(1-\tau )\cdot \text{sigmoid}(-\theta )}\end{array}\end{array}$$
其中$\tau \in (0,1)$是一个常数，笔者在自己的实验中取了$\tau =0.5$，而$\theta$是可训练参数，上式利用了恒等式$\text{sigmoid}(-\theta )=1-\text{sigmoid}(\theta )$。

关键代码参考（Keras）：

class Scaler(Layer):
    """特殊的scale层
    """
    def __init__(self, tau=0.5, **kwargs):
        super(Scaler, self).__init__(**kwargs)
        self.tau = tau

def build(self, input_shape):
    super(Scaler, self).build(input_shape)
    self.scale = self.add_weight(
        name='scale', shape=(input_shape[-1],), initializer='zeros'
    )

def call(self, inputs, mode='positive'):
    if mode == 'positive':
        scale = self.tau + (1 - self.tau) * K.sigmoid(self.scale)
    else:
        scale = (1 - self.tau) * K.sigmoid(-self.scale)
    return inputs * K.sqrt(scale)

def get_config(self):
    config = {'tau': self.tau}
    base_config = super(Scaler, self).get_config()
    return dict(list(base_config.items()) + list(config.items()))




def sampling(inputs):

"""重参数采样

"""

z_mean, z_std = inputs

noise = K.random_normal(shape=K.shape(z_mean))

return z_mean + z_std * noise


def build(self, input_shape):
    super(Scaler, self).build(input_shape)
    self.scale = self.add_weight(
        name='scale', shape=(input_shape[-1],), initializer='zeros'
    )

def call(self, inputs, mode='positive'):
    if mode == 'positive':
        scale = self.tau + (1 - self.tau) * K.sigmoid(self.scale)
    else:
        scale = (1 - self.tau) * K.sigmoid(-self.scale)
    return inputs * K.sqrt(scale)

def get_config(self):
    config = {'tau': self.tau}
    base_config = super(Scaler, self).get_config()
    return dict(list(base_config.items()) + list(config.items()))
e_outputs  # 假设e_outputs是编码器的输出向量

scaler = Scaler()

z_mean = Dense(hidden_dims)(e_outputs)

z_mean = BatchNormalization(scale=False, center=False, epsilon=1e-8)(z_mean)

z_mean = scaler(z_mean, mode='positive')

z_std = Dense(hidden_dims)(e_outputs)

z_std = BatchNormalization(scale=False, center=False, epsilon=1e-8)(z_std)

z_std = scaler(z_std, mode='negative')

z = Lambda(sampling, name='Sampling')([z_mean, z_std])

文章内容小结 #

本文简单分析了VAE在NLP中的KL散度消失现象，并介绍了通过BN层来防止KL散度消失、稳定训练流程的方法。这是一种简洁有效的方案，不单单是原论文，笔者私下也做了简单的实验，结果确实也表明了它的有效性，值得各位读者试用。因为其推导具有一般性，所以甚至任意场景（比如CV）中的VAE模型都可以尝试一下。

转载到请包括本文地址：https://spaces.ac.cn/archives/7381

更详细的转载事宜请参考：《科学空间FAQ》