(六)大模型RLHF:PPO原理与源码解读
大模型RLHF:PPO原理与源码解读
本文直接从一个RLHF开源项目源码入手(deepspeed-chat),根据源码的实现细节,给出尽可能丰富的训练流程图,并对所有的公式给出直观的解释。希望可以帮助大家更具象地感受RLHF的训练流程。关于RLHF,各家的开源代码间都会有一些差异,同时也不止PPO一种RLHF方式。
1.强化学习概述
1.1 强化学习整体流程
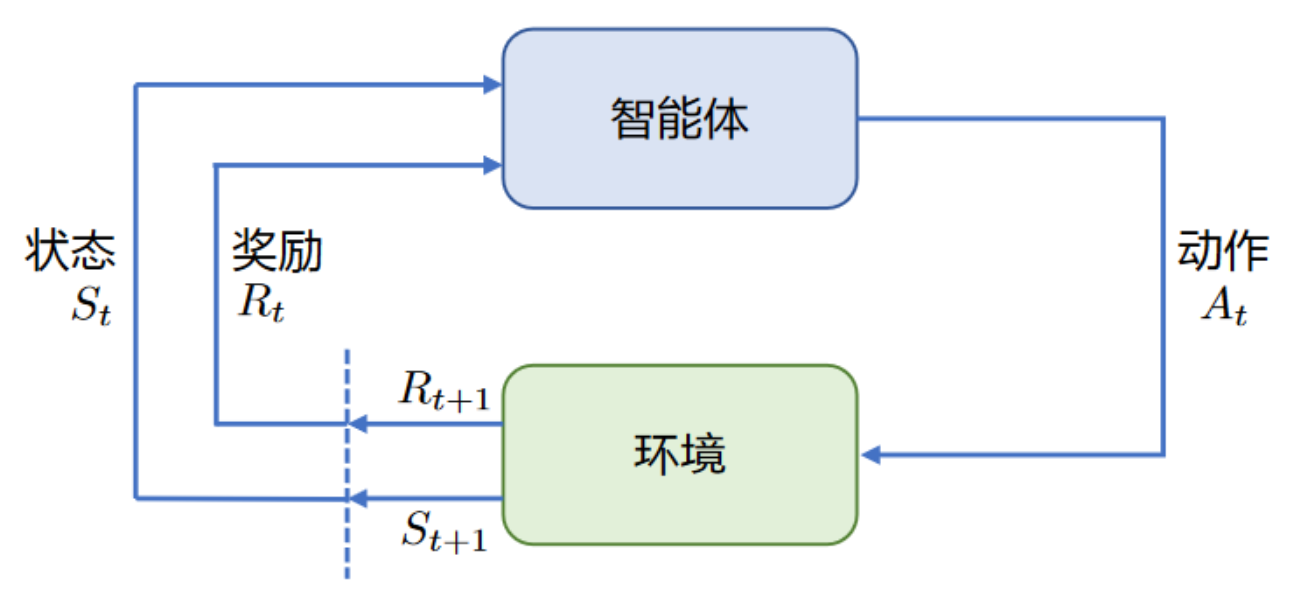
强化学习的两个实体:智能体(Agent)与环境(Environment)
强化学习中两个实体的交互:
- 状态空间S:S即为State,指环境中所有可能状态的集合
- 动作空间A:A即为Action,指智能体所有可能动作的集合
- 奖励R**:** R即为Reward,指智能体在环境的某一状态下所获得的奖励。
以上图为例,智能体与环境的交互过程如下:
- 在
t时刻,环境的状态为 \(S_{t}\) ,达到这一状态所获得的奖励为 \(R_{t}\) - 智能体观测到 \(S_{t}\) 与 \(R_{t}\) ,采取相应动作 \(A_{t}\)
- 智能体采取 \(A_{t}\) 后,环境状态变为 \(S_{t+1}\) ,得到相应的奖励 \(R_{t+1}\)
智能体在这个过程中学习,它的最终目标是:找到一个策略,这个策略根据当前观测到的环境状态和奖励反馈,来选择最佳的动作。
1.2 价值函数
在1.1中,谈到了奖励值 \(R_{t}\) ,它表示环境进入状态 \(S_{t}\) 下的即时奖励。但如果只考虑即时奖励,目光似乎太短浅了:当下的状态和动作会影响到未来的状态和动作,进而影响到未来的整体收益。所以,一种更好的设计方式是:t时刻状态s的总收益 = 身处状态s能带来的即时收益 + 从状态s出发后能带来的未来收益**。** 写成表达式就是:
其中:
- \(V_{t}\) :
t时刻的总收益,注意这个收益蕴涵了“即时”和“未来”的概念 - \(R_{t}\) :
t时刻的即时收益 - \(V_{t+1}\) :
t+1时刻的总收益,注意这个收益蕴涵了“即时”和“未来”的概念。而 \(V_{t+1}\) 对 \(V_{t}\) 来说就是“未来”。 - \(\gamma\) :折扣因子。它决定了我们在多大程度上考虑将“未来收益”纳入“当下收益”。
注:在这里,不展开讨论RL中关于价值函数的一系列假设与推导,而是直接给出一个便于理解的简化结果,方便没有RL背景的朋友能倾注更多在“PPO策略具体怎么做”及“对PPO的直觉理解”上。
2.NLP中的强化学习
在第一部分介绍了通用强化学习的流程,那么要怎么把这个流程对应到NLP任务中呢?换句话说,NLP任务中的智能体、环境、状态、动作等等,都是指什么呢?
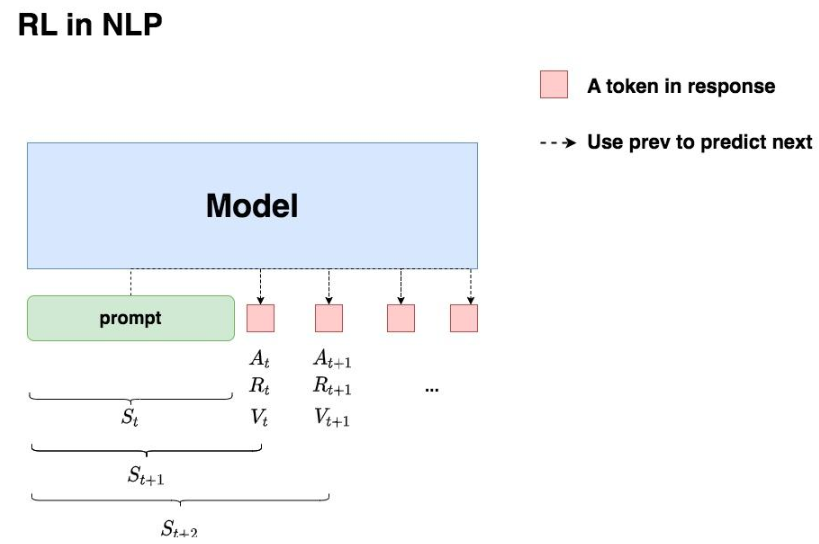
回想一下对NLP任务做强化学习(RLHF)的目的:希望给模型一个prompt,让模型能生成符合人类喜好的response。再回想一下GPT模型做推理的过程:每个时刻 t 只产生一个token,即token是一个一个蹦出来的,先有上一个token,再有下一个token**。**
复习了这两点,现在可以更好解读上面这张图了:
- 先喂给模型一个prompt,期望它能产出符合人类喜好的response
- 在
t时刻,模型根据上文,产出一个token,这个token即对应着强化学习中的动作,记为 \(A_{t}\) 。因此不难理解,在NLP语境下,强化学习任务的动作空间就对应着词表。 - 在
t时刻,模型产出token \(A_{t}\) 对应着的即时收益为 \(R_{t}\) ,总收益为 \(V_{t}\)。这个收益即可以理解为“对人类喜好的衡量”。此刻,模型的状态从 \(S_{t}\) 变为 \(S_{t+1}\) ,也就是从“上文”变成“上文 + 新产出的token” - 在NLP语境下,智能体是语言模型本身,环境则对应着它产出的语料
这样,就大致解释了NLP语境下的强化学习框架,不过针对上面这张图,可能还有以下问题:
(1)问题1: 图中的下标是不是写得不太对?例如根据第一部分的介绍,\(A_{t}\) 应该对应着 \(R_{t+1}\) , \(A_{t+1}\) 应该对应着 \(R_{t+2}\) ,以此类推?
答:说的对。但这里不用太纠结下标的问题,只需要记住在对应的response token位置,会产生相应的即时奖励和总收益即可。之所以用图中这样的下标,是更方便后续理解代码。
(2)问题2: 知道\(A_{t}\) 肯定是由语言模型产生的,那么 \(R_t\),$ V_{t} $是怎么来的呢,也是语言模型产生的吗?
答:先直接说结论, $ A_{t} $是由我们的语言模型产生的, \(R_{t}\),\(V_{t}\) 则分别由另外两个模型来产生,在后文中会细说。
(3)问题3: 语言模型的参数在什么时候更新?是观测到一个\(R_{t}\), $ V_{t} $,就更新一次参数,然后再去产生 \(A_{t+1}\) 吗?
答:当然不是。只看到某个时刻的收益,就急着用它更新模型,这也太莽撞了。肯定是要等有足够的观测数据了(例如等模型把完整的response生成完),再去更新它的参数。
(4)问题4: 再谈谈\(R_{t},\) \(V_{t}\) 吧,在NLP的语境下我还是不太理解它们
- 首先,“收益”的含义是“对人类喜好的衡量”
- \(R\_{t}\) :即时收益,指语言模型当下产生token \(A_{t}\) 带来的收益
- \(V_{t}\) : 实际期望总收益(即时+未来),指对语言模型“当下产生token \(A_{t}\) ,一直到整个response生产结束”后的期收益预估。因为当下语言模型还没产出 \(A_{t}\) 后的token,所以只是对它之后一系列动作的收益做了估计,因而称为“期望总收益”。
3.RLHF中的四个重要角色
本节中,在第二部分的基础上更进一步:更详细理清NLP语境下RLHF的运作流程。
从第二部分中已经知道:生成token \(A_{t}\) 和对应收益 \(R_{t}\), \(V_{t}\) 的并不是一个模型。那么在RLHF中到底有几个模型?他们是怎么配合做训练的?而我们最终要的是哪个模型?
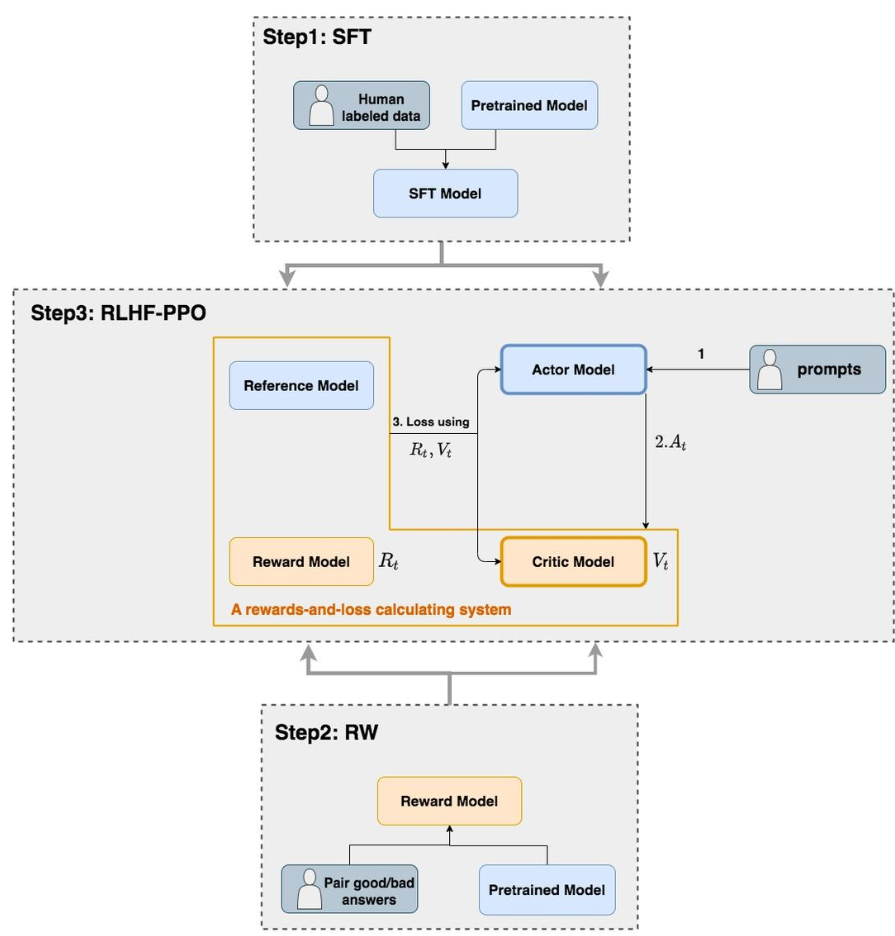
如上图,在RLHF-PPO阶段,一共有四个主要模型,分别是:
- Actor Model**:演员模型**,这就是想要训练的目标语言模型
- Critic Model**:评论家模型**,它的作用是**预估总收益 **\(V_{t}\)
- Reward Model**:奖励模型**,它的作用是**计算即时收益 **\(R_{t}\)
- Reference Model**:参考模型**,它的作用是在RLHF阶段给语言模型增加一些“约束”,防止语言模型训歪(朝不受控制的方向更新,效果可能越来越差)
其中:
- Actor/Critic Model在RLHF阶段是需要训练的(图中给这两个模型加了粗边,就是表示这个含义);而Reward/Reference Model是参数冻结的。
- Critic/Reward/Reference Model共同组成了一个“奖励-loss”计算体系(自己命名的,为了方便理解),综合它们的结果计算loss,用于更新Actor和Critic Model
我们把这四个部分展开说说。
3.1 Actor Model (演员模型)
正如前文所说,Actor就是想要训练的目标语言模型。一般用SFT阶段产出的SFT模型来对它做初始化。
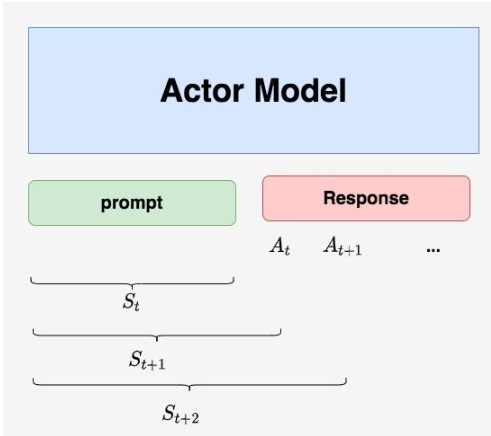
最终目的是让Actor模型能产生符合人类喜好的response。所以策略是,先喂给Actor一条prompt (这里假设batch_size = 1,所以是1条prompt),让它生成对应的response。然后,再将“prompt + response"送入我们的“奖励-loss”计算体系中去算得最后的loss,用于更新actor。
3.2 Reference Model(参考模型)
Reference Model(以下简称Ref模型)一般也用SFT阶段得到的SFT模型做初始化,在训练过程中,它的参数是冻结的。 Ref模型的主要作用是防止Actor“训歪”,那么它具体是怎么做到这一点的呢?
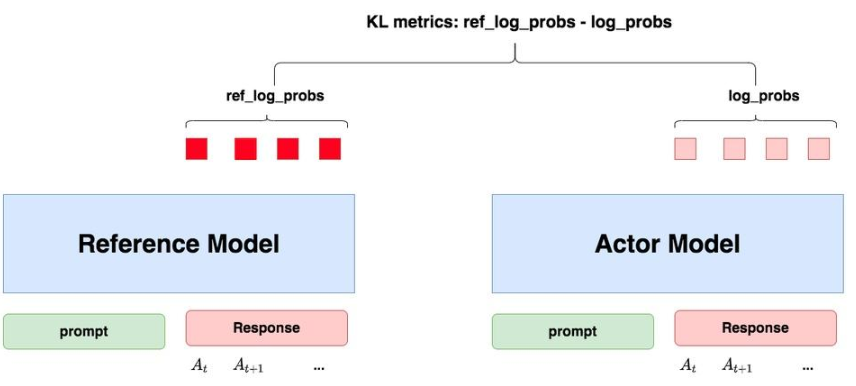
“防止模型训歪”换一个更详细的解释是:希望训练出来的Actor模型既能达到符合人类喜好的目的,又尽量让它和SFT模型不要差异太大。简言之,希望两个模型的输出分布尽量相似。那什么指标能用来衡量输出分布的相似度呢?自然而然想到了KL散度。
如图所示:
- 对Actor模型,喂给它一个
prompt,它正常输出对应的response。那么response中每一个token肯定有它对应的log_prob结果,把这样的结果记为**log_probs** - 对Ref模型,把Actor生成的
"prompt + response"喂给它,那么它同样能给出每个token的log_prob结果,我们记其为**ref_log_probs** - 那么这两个模型的输出分布相似度就可以用
ref_log_probs - log_probs来衡量,可以从两个方面来理解这个公式:- 从直觉上理解,
ref_log_probs越高,说明Ref模型对Actor模型输出的肯定性越大。即Ref模型也认为,对于某个 \(S_{t}\) ,输出某个 \(A_{t}\) 的概率也很高$ P(A_{t} | S_{t}) $)。这时可以认为Actor模型较Ref模型没有训歪。 - 从KL散度上理解, $ KL[Actor(X) || Ref(X)] = E_{x\sim Actor(x)}[log\frac{Actor(x)}{Ref(x)}] = log_probs - ref_log_probs $(当然这里不是严格的等于,只是KL散度的近似),这个值越小意味着两个分布的相似性越高。
- 从直觉上理解,
注:可能已经注意到,按照KL散度的定义,这里写成log_probs - ref_log_probs更合适一些。但是如果你看过一些RLHF相关的论文的话,可能记得在计算损失函数时,有一项 \(R_{t} - KL\)散度 (对这个有疑惑不要紧,我们马上在后文细说),即KL散度前带了负号,所以这里我写成ref_log_probs - log_probs这样的形式,更方便大家从直觉上理解这个公式。
现在,已经知道怎么利用Ref模型和KL散度来防止Actor训歪了。KL散度将在后续被用于loss的计算。
3.3 Critic Model(评论家模型)
Critic Model用于预测期望总收益 **\(V_{t}\) **,和Actor模型一样,它需要做参数更新。实践中,Critic Model的设计和初始化方式也有很多种,例如和Actor共享部分参数、从RW阶段的Reward Model初始化而来等等。我们讲解时,和deepspeed-chat的实现保持一致:从RW阶段的Reward Model初始化而来。
你可能想问:训练Actor模型我能理解,但我还是不明白,为什么要单独训练一个Critic模型用于预测收益呢?
这是因为,当我们在前文讨论总收益 \(V_{t}\) (即时 + 未来)时,我们是站在上帝视角的,也就是这个 \(V_{t}\) 就是客观存在的、真正的总收益。但是在训练模型时,就没有这个上帝视角加成了,也就是在
t时刻,给不出客观存在的总收益 \(V_{t}\) ,只能训练一个模型去预测它**。**
所以总结来说,在RLHF中,不仅要训练模型生成符合人类喜好的内容的能力(Actor),也要提升模型对人类喜好量化判断的能力(Critic)。这就是Critic模型存在的意义。来看看它的大致架构:
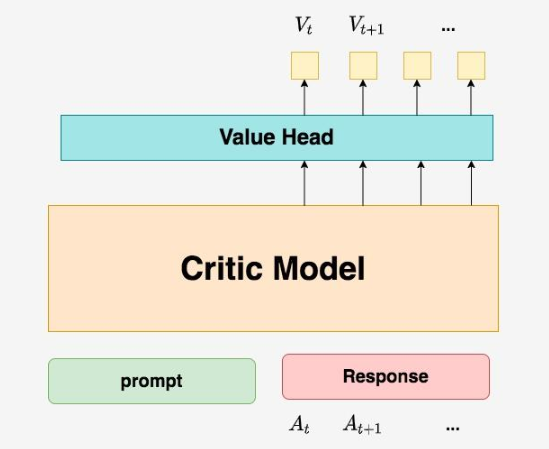
deepspeed-chat采用了Reward模型作为它的初始化,所以这里也按Reward模型的架构来简单画画它。你可以简单理解成,Reward/Critic模型和Actor模型的架构是很相似的(毕竟输入都一样),同时,它在最后一层增加了一个Value Head层,该层是个简单的线形层,用于将原始输出结果映射成单一的 \(V\_{t}\) 值。
在图中, \(V\_{t}\) 表示Critic模型对 t 时刻及未来(response完成)的收益预估。
3.4 Reward Model(奖励模型)
Reward Model用于计算生成token \(A_{t}\) 的即时收益,它就是RW阶段所训练的奖励模型,在RLHF过程中,它的参数是冻结的。
你可能想问:为什么Critic模型要参与训练,而同样是和收益相关的Reward模型的参数就可以冻结呢? 这是因为,Reward模型是站在上帝视角的。这个上帝视角有两层含义:
- 第一点,Reward模型是经过和“估算收益”相关的训练的,因此在RLHF阶段它可以直接被当作一个能产生客观值的模型。
- 第二点,Reward模型代表的含义就是“即时收益”,你的token \(A_{t}\) 已经产生,因此即时收益自然可以立刻算出。
你还可能想问:已经用Critic预测出 \(V_{t}\) 了,而这个 \(V_{t}\) 包含了“即时”和“未来”的概念,那还需要代表“即时”的 \(R_{t}\) 做什么呢?直接用 \(V_{t}\) 不就好了吗?
为了解答这个问题,先回顾下1.2部分中给出的价值函数: $ V_{t} = R_{t} + \gamma V_{t+1} $
这个函数告诉我们,当前可以用两个结果来表示 t 时刻的总收益:
- 结果1:Critic模型预测的 \(V_{t}\)
- 结果2:Reward模型预测的 \(R_{t}\) 和critic模型预测的 \(V_{t+1}\)
那么哪一个结果更靠近上帝视角给出的客观值呢?当然是结果2,因为结果1全靠预测,而结果2中的 \(R_{t}\) 是事实数据。我们知道Critic模型也是参与参数更新的,可以用MSE(上帝视角的客观收益-Critic模型预测的收益)来衡量它的loss。但是上帝视角的客观收益是不知道的,只能用已知事实数据去逼近它,所以我们就用 $ R_{t} + \gamma * V_{t+1} $来做近似。 这就是 $ R_{t}, V_{t} $同时存在的意义。
Reward模型和critic模型非常相似,这里就只给出架构图,不再做过多的说明。关于Reward模型的训练过程,后续有时间也会出个原理和代码解析。
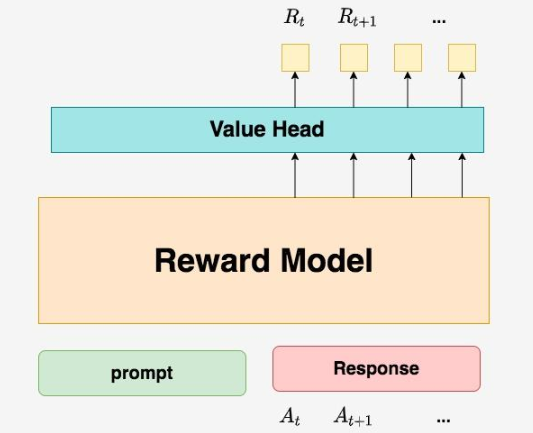
4.RLHF中的loss计算
到目前为止,已经基本了解了RLHF的训练框架,以及其中的四个重要角色(训练一个RLHF,有4个模型在硬件上跑,可想而知对存储的压力)。在本节中,一起来解读RLHF的loss计算方式。在解读中,会再一次理一遍RLHF的整体训练过程,填补相关细节。在这之后,就可以来看代码解析了。
在第三部分的讲解中,我们知道Actor和Critic模型都会做参数更新,所以loss也分成2个:
- Actor loss: 用于评估Actor是否产生了符合人类喜好的结果,将作用于Actor的BWD上。
- Critic loss**:** 用于评估Critic是否正确预测了人类的喜好,将作用于Critic的BWD上。
4.1 Actor loss
(1)直观设计
先来看一个直观的loss设计方式:
- Actor接收到当前上文 \(S_{t}\) ,产出token \(A_{t}\) ( \(P(A_{t} | S_{t})\) )
- Critic根据 \(S_{t}\), \(A_{t}\) ,产出对总收益的预测 \(V_{t}\)
- 那么Actor loss可以设计为: \(actor\_loss =- \sum_{t \in { response\_timestep }} V_{t} \log P (A_{t} | S_{t})\)
求和符号表示只考虑response部分所有token的loss,为了表达简便,先把这个求和符号略去(下文也是同理),也就是说:
我们希望minimize这个actor_loss。
这个设计的直观解释是:
- 当 \(V_{t}>0\) 时,意味着Critic对Actor当前采取的动作给了正向反馈,因此就需要在训练迭代中提高 $ P(A_{t} | S_{t}) $,这样就能达到减小loss的作用。
- 当 \(V_{t} < 0\) 时,意味着Critic对Actor当前采取的动作给了负向反馈,因此就需要在训练迭代中降低 \(P(A_{t} | S_{t})\) ,这样就能到达到减小loss的作用。
一句话总结:这个loss设计的含义是,****对上文 \(S_{t}\) 而言,如果token \(A_{t}\) 产生的收益较高,那就增大它出现的概率,否则降低它出现的概率****。
(2)引入优势(Advantage)
在开始讲解之前,举个小例子:假设在王者中,中路想支援发育路,这时中路有两种选择:1. 走自家野区。2. 走大龙路。中路选择走大龙路,当做出这个决定后,Critic告诉她可以收1个人头。结果,此刻对面打野正在自家采灵芝,对面也没有什么苟草英雄,中路一路直上,最终收割2个人头。因为实际收割的人头比预期要多1个,中路尝到了甜头,所以增大了“支援发育路走大龙路”的概率。这个多出来的“甜头”,就叫做“优势”(Advantage)。
对NLP任务来说,如果Critic对 \(A_{t}\) 的总收益预测为 \(V_{t}\) ,但实际执行 \(A_{t}\) 后的总收益是 \(R_{t} + \gamma * V_{t+1}\) ,我们就定义优势为:
用 \(Adv_{t}\) 替换掉 $ V_{t} \(,则此刻`actor_loss`变为: \)actor_loss = -Adv_{t}log P(A_{t}|S_{t})$
(3)重新设计 \(R_{t}\)
总结一下,到目前为止,我们的actor_loss形式为:
其中, $ Adv_{t} = R_{t} + \gamma * V_{t+1} - V_{t} $
同时注意,这个actor_loss应该是response的所有token loss的sum或者avg。这里为了表达方便,公式略去了求和或求平均的符号。
按照这个理解, \(R_{t}\) 应该表示每个Actor产出token \(A_{t}\) 带来的即时收益,正如下图所示(其中 T 表示最后一个时刻):
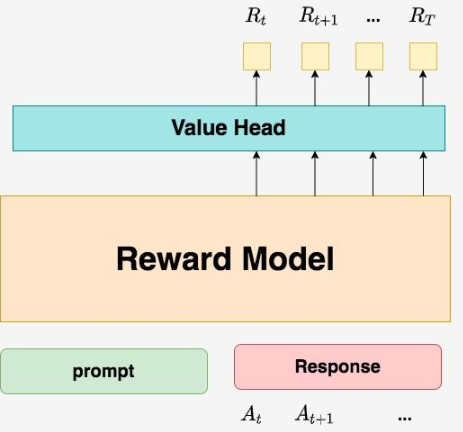
但在deepspeed-chat的RLHF实践中,对 \(R_{t}\) 做了另一种设计:
kl_ctl:常量,可以理解成是一个控制比例的缩放因子,在deepspeed-chat中默认设为0.1- $ -log\frac{P(A_{t}|S_{t})}{P_{ref}(A_{t}|S_{t})} $:这一项是不是非常眼熟,这就是在3.2部分介绍的Actor和Ref模型间的KL散度,写成更容易理解的形式,就是
ref_log_probs - log_probs。在3.2中说过,为了防止模型训歪,需要把这个KL散度加入loss计算中,所以这里我们就在做这件事
基于这些,上面这个对 \(R_{t}\) 的设计可理解成:
- 当 \(t \neq T\) 时,更加关心Actor是否有在Ref的约束下生产token \(A_{t}\)
- 当\(t =T\) 时,不仅关心Actor是否遵从了Ref的约束,也关心真正的即时收益 \(R_{t}\)
为什么只有最后一个时刻的 \(R_{t}\) 被纳入了考量呢?这是因为在Reward模型训练的时候,就是用这个位置的 \(R_{t}\) 来表示对完整的prompt + response的奖励预测(但你依然可以理解成是执行完 \(A_{T}\) 的即时奖励)。所以到了RLHF的场景下,其余时刻的即时奖励,就用“Actor是否遵循了Ref的约束”来进行评价。
需要注意的是, \(R_{t}\) 的设计并不只有这一种。deepspeed在自己的代码注释中也有提过,可以尝试把最后一个时刻的 \(R_{T}\) 替换成所有token的即时奖励的平均值(因为在Reward模型中,每一个token位置照样会有对应的奖励值输出,只是它们不像最后一个位置那样用对应的真值经过了训练,这个真值就是指人标注的对整个prompt + response的奖励真值)。如果站在这个角度理解的话,同样也可以尝试在每一个位置的奖励衡量上引入 \(R_{t}\) 。
代码实践如下:
def compute_rewards(self, prompts, log_probs, ref_log_probs, reward_score,
action_mask):
"""
reward_function:计算最终的reward分数
复习一下几个相关参数的默认值:
self.kl_ctl = 0.1
self.clip_reward_value = 5
对于batch中的某个prompt来说,它最终的reward分数为:
(1) 先计算actor和ref_model的logit相似度: -self.kl_ctl * (log_probs - ref_log_probs)
其实写成self.kl_ctl * (ref_log_probs - log_probs)更好理解些
这个值越大,说明ref_model对actor生成的结果的认可度越高(即表明rlhf没有训歪),
没有训歪的情况下我们也应该给模型一些奖励,这个奖励就是self.kl_ctl * (ref_log_probs - log_probs)
(2)由于我们只取最后一个token对应位置的分数作为reward_score,因此我们只需要:
self.kl_ctl * (ref_log_probs - log_probs)的最后一位 + reward_score
(3) 同时我们对reward_score也做了大小限制,最大不超过self.clip_reward_value(超过统一给成self.clip_reward_value),
最小不低于-self.clip_reward_value(低于统一给成-self.clip_reward_value)
(4) 最后返回的rewards大小为:(batch_size, 各条数据的长度),对batch中的每条数据来说:
- response的最后一位:self.kl_ctl * (ref_log_probs - log_probs)的最后一位 + reward_score
- response的其余位置:self.kl_ctl * (ref_log_probs - log_probs)
"""
kl_divergence_estimate = -self.kl_ctl * (log_probs - ref_log_probs)
rewards = kl_divergence_estimate
# ---------------------------------------------------------------------------------------------------
# response开始的位置
# (因为我们对prompt做过padding处理,因此batch中每个prompt长度一致,也就意味着每个response开始的位置一致)
# (所以这里start是不加s的,只是一个int)
# ---------------------------------------------------------------------------------------------------
start = prompts.shape[1] - 1
# ---------------------------------------------------------------------------------------------------
# response结束的位置
# (因为一个batch中,每个response的长度不一样,所以response的结束位置也不一样)
# (所以这里end是加s的,ends的尺寸是(batch_size,)
# ---------------------------------------------------------------------------------------------------
ends = start + action_mask[:, start:].sum(1) + 1
# ---------------------------------------------------------------------------------------------------
# 对rewards_score做限制
# ---------------------------------------------------------------------------------------------------
reward_clip = torch.clamp(reward_score, -self.clip_reward_value,
self.clip_reward_value)
batch_size = log_probs.shape[0]
for j in range(batch_size):
rewards[j, start:ends[j]][-1] += reward_clip[j] #
return rewards
(4)重新设计优势
好,再总结一下,目前为止的actor_loss为:
其中, $ Adv_{t} = R_{t} + \gamma * V_{t+1} - V_{t} $
同时,对 \(R_{t}\) 进行来改造,使其能够衡量Actor模型是否遵从了Ref模型的约束。
现在把改造焦点放在 \(Adv_{t}\) 上,回想一下,既然对于收益而言,分为即时和未来,那么对于优势而言,是不是也能引入对未来优势的考量呢?这样,就可以把 \(Adv_{t}\) 改写成如下形式:
(熟悉强化学习的朋友应该能一眼看出这是GAE,这里不打算做复杂的介绍,一切都站在直觉的角度理解)其中,新引入的 \(\lambda\) 也是一个常量,可将其理解为权衡因子,直觉上看它控制了在计算当前优势时对未来优势的考量。(从强化学习的角度上,它控制了优势估计的方差和偏差)
看到这里,你可能想问:这个代表未来优势的 $ Adv_{t+1} \(**,那要怎么算呢?** 注意到,对于最后一个时刻`t` ,它的未来收益(\)V_{T+1}$ )和未来优势(\(Adv_{T+1}\) )都是0,也就是 \(Adv_{T} = R_{T} - V_{T}\) ,这是可以直接算出来的。而有了 \(Adv_{T}\) ,不就能从后往前,通过动态规划的方法,把所有时刻的优势都依次算出来了吗?
代码实践如下(其中返回值中的returns表示实际收益,将被用于计算Critic模型的loss,可以参见4.2,其余细节都在代码注释中):
def get_advantages_and_returns(self, values, rewards, start):
"""
Adopted from https://github.com/CarperAI/trlx/blob/main/trlx/models/modeling_ppo.py#L134
没有引入GAE前的t时刻的优势值·:
detal_t = r_t + gamma * V_t+1 - V_t
其中:
- r_t表示t时刻的即时收益
- V_t+1表示未来时刻的预期收益
- r_t + gamma * V_t+1可理解成t时刻的实际预期收益
- V_t可理解成t时刻的预估预期收益(是模型,例如critic model自己估算出来的)
引入GAE后的t时刻的优势值:
A_t = delta_t + gamma * lambda * A_t+1
粗暴理解为在t时刻时,不仅考虑当下优势,还考虑了未来的优势
为了知道A_t, 我们得知道A_t+1,所以在本算法中采取了从后往前做动态规划求解的方法,也即:
假设T是最后一个时刻,则有A_T+1 = 0, 所以有: A_T = delta_T
知道了A_T, 就可以依次往前倒推,把A_t-1, A_t-2之类都算出来了
引入GAE后t时刻的实际预期收益
returns_t = A_t + V_t
= delta_t + gamma * lambda * A_t+1 + V_t
= r_t + gamma * V_t+1 - V_t + gamma * lambda * A_t+1 + V_t
= r_t + gamma * (V_t+1 + lambda * A_t+1)
注意,这里不管是advantages还是returns,都只算response的部分
"""
# Adopted from https://github.com/CarperAI/trlx/blob/main/trlx/models/modeling_ppo.py#L134
lastgaelam = 0
advantages_reversed = []
length = rewards.size()[-1]
# 注意这里用了reversed,是采取从后往前倒推计算的方式
for t in reversed(range(start, length)):
nextvalues = values[:, t + 1] if t < length - 1 else 0.0
delta = rewards[:, t] + self.gamma * nextvalues - values[:, t]
lastgaelam = delta + self.gamma * self.lam * lastgaelam
advantages_reversed.append(lastgaelam)
advantages = torch.stack(advantages_reversed[::-1], dim=1) # 优势
returns = advantages + values[:, start:] # 实际收益
# values: 预期收益
return advantages.detach(), returns
(5)PPO-epoch: 引入新约束
总结一下,目前为止的actor_loss为:
其中, $ Adv_{t} = (R_{t} + \gamma * V_{t+1} - V_{t}) + \gamma * \lambda * Adv_{t+1} $
同时
- 已经对 \(R_{t}\) 进行来改造,使其能够衡量Actor模型是否遵从了Ref模型的约束。
- 已经对\(Adv_{t}\) 进行改造,使其不仅考虑了当前时刻的优势,还考虑了未来的优势
基于这些改造,重新理一遍RLHF-PPO的训练过程。
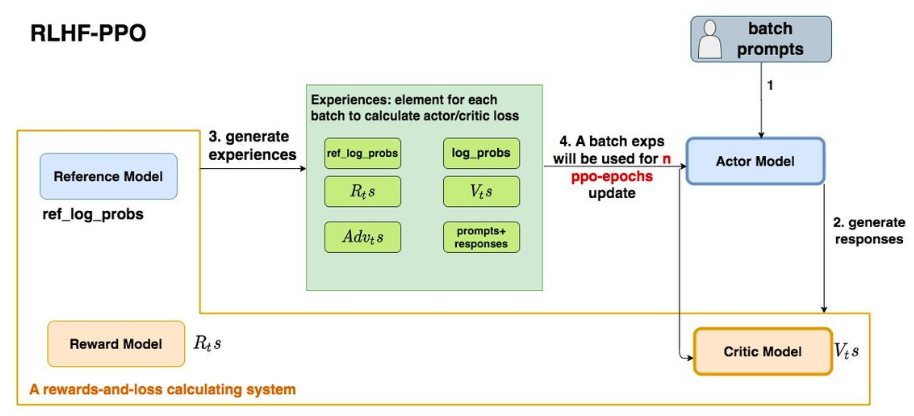
- 第一步,准备一个batch的prompts
- 第二步,将这个batch的prompts喂给Actor模型,让它生成对应的responses
- 第三步,把prompt+responses喂给我们的Critic/Reward/Reference模型,让它生成用于计算actor/critic loss的数据,按照强化学习的术语,称这些数据为经验(experiences)。critic loss我们将在后文做详细讲解,目前只把目光聚焦到actor loss上
- 第四步,根据这些经验,实际计算出actor/critic loss,然后更新Actor和Critic模型
这些步骤都很符合直觉,但是细心的你肯定发现了,文字描述中的第四步和图例中的第四步有差异:图中说,这一个batch的经验值将被用于n次模型更新,这是什么意思呢?
在强化学习中,收集一个batch的经验是非常耗时的。对应到RLHF的例子中,收集一次经验,它要等四个模型做完推理才可以,正是因此,一个batch的经验,只用于计算1次loss,更新1次Actor和Critic模型,好像有点太浪费了。
所以,自然而然想到,1个batch的经验,能不能用来计算ppo-epochs次loss,更新ppo-epochs次Actor和Critic模型? 简单写一下伪代码,我们想要:
# --------------------------------------------------------------
# 初始化RLHF中的四个模型
# --------------------------------------------------------------
actor, critic, reward, ref = initialize_models()
# --------------------------------------------------------------
# 训练
# --------------------------------------------------------------
# 对于每一个batch的数据
for i in steps:
# 先收集经验值
exps = generate_experience(prompts, actor, critic, reward, ref)
# 一个batch的经验值将被用于计算ppo_epochs次loss,更新ppo_epochs次模型
# 这也意味着,当你计算一次新loss时,你用的是更新后的模型
for j in ppo_epochs:
actor_loss = cal_actor_loss(exps, actor)
critic_loss = cal_critic_loss(exps, critic)
actor.backward(actor_loss)
actor.step()
critc.backward(critic_loss)
critic.step()
而如果想让一个batch的经验值被重复使用ppo_epochs次,等价于想要Actor在这个过程中,模拟和环境交互**ppo_epochs**次。 举个例子:
- 如果1个batch的经验值只使用1次,那么在本次更新完后,Actor就吃新的batch,正常和环境交互,产出新的经验值
- 但如果1个batch的经验值被使用
ppo_epochs次,在这ppo_epochs中,Actor是不吃任何新数据,不做任何交互的,所以只能让Actor“模拟”一下和环境交互的过程,吐出一些新数据出来。
那怎么让Actor模拟呢?很简单,让它观察一下之前的数据长什么样,让它依葫芦画瓢,不就行了吗?假设最开始吃batch,吐出经验的actor叫\(Actor_{old}\) ,而在伪代码中,每次做完**ppo_epochs**而更新的actor叫 \(Actor_{new}\) ,那么只要尽量保证每次更新后的 \(Actor_{new}\) 能模仿最开始的那个 \(Actor_{old}\) ,不就行了吗?
诶!是不是很眼熟!两个分布,通过什么方法让它们相近!那当然是KL散度!所以,再回到我们的actor_loss上来,它现在就可被改进成:\(actor\_loss = -Adv_{t}log \frac{P(A_{t}|S_{t})}{P_{old}(A_{t}|S_{t})}\)
再稍作一些改动将log去掉(这个其实不是“稍作改动去掉log”的事,是涉及到PPO中重要性采样的相关内容,大家有兴趣可以参考这篇):\(actor\_loss = -Adv_{t} * \frac{P(A_{t}|S_{t})}{P_{old}(A_{t}|S_{t})}\)
其中,\(P_{old}\) 表示真正吃了batch,产出经验值的Actor;P表示ppo_epochs中实时迭代更新的Actor,它在模仿 $ P_{old} $的行为。所以这个公式从直觉上也可以理解成:在Actor想通过模拟交互的方式,使用一个batch的经验值更新自己时,它需要收到真正吃到batch的那个时刻的Actor的约束,这样才能在有效利用batch,提升训练速度的基础上,保持训练的稳定。
但是,此时又有新的担心了:虽然在更新Actor的过程中用 \(Actor_{old}\) 做了约束,但如果 \(Actor_{old}\) 的约束能力不够,比如说 $ \frac{P(A_{t} | S_{t})}{P_{old}(A_{t} | S_{t})} $还是超出了可接受的范围,那怎么办?
很简单,那就剪裁(clip) 它吧!
我们给 \(\frac{P(A_{t} | S_{t})}{P_{old}(A_{t} | S_{t})}\) 设置一个范围,例如(0.8 ,1.2),也就是如果这个值一旦超过1.2,那就统一变成1.2;一旦小于0.8,那就统一变成0.8。这样就能保证 $ Actor \(和\)Actor_{old}$ 的分布相似性在我们的掌控之内了。此时actor_loss变为:
这时要注意,如果超过变化范围,将 \(\frac{P(A_{t} | S_{t})}{P_{old}(A_{t} | S_{t})}\) 强制设定为一个常数后,就说明这一部分的loss和Actor模型无关了,而 \(Adv_{t}\) 这项本身也与Actor无关。所以相当于,在超过约束范围时,我们停止对Actor模型进行更新。
整体代码如下:
def actor_loss_fn(self, logprobs, old_logprobs, advantages, mask):
"""
logprobs: 实时计算的,response部分的prob(只有这个是随着actor实时更新而改变的)
old_logprobs:老策略中,response部分的prob (这个是固定的,不随actor实时更新而改变)
advantages: 老策略中,response部分每个token对应的优势(这个是固定的,不随actor实时更新而改变)
mask:老策略中,response部分对应的mask情况这个是固定的,不随actor实时更新而改变)
之所以要引入logprobs计算actor_loss,是因为我们不希望策略每次更新的幅度太大,防止模型训歪
self.cliprange: 默认值是0.2
"""
## policy gradient loss
# -------------------------------------------------------------------------------------
# 计算新旧策略间的KL散度
# -------------------------------------------------------------------------------------
log_ratio = (logprobs - old_logprobs) * mask
ratio = torch.exp(log_ratio)
# -------------------------------------------------------------------------------------
# 计算原始loss和截断loss
# -------------------------------------------------------------------------------------
pg_loss1 = -advantages * ratio
pg_loss2 = -advantages * torch.clamp(ratio, 1.0 - self.cliprange, 1.0 + self.cliprange)
pg_loss = torch.sum(torch.max(pg_loss1, pg_loss2) * mask) / mask.sum() # 最后是取每个非mask的response token的平均loss作为最终loss
return pg_loss
(6)Actor loss小结
(1)~(5)中我们一步步树立了actor_loss的改进过程,这里就做一个总结吧:
其中:
- \(A d v_{t}=\left(R_{t}+\gamma * V_{t+1}-V_{t}\right)+\gamma * \lambda * A d v_{t+1}\)
- 已经对 \(R_{t}\) 进行来改造,使其能够衡量Actor模型是否遵从了Ref模型的约束
- 已经对 $ Adv_{t} $进行改造,使其不仅考虑了当前时刻的优势,还考虑了未来的优势
- 重复利用了1个batch的数据,使本来只能被用来做1次模型更新的它现在能被用来做**
ppo_epochs次模型更新。使用真正吃了batch,产出经验值的那个时刻的Actor分布来约束ppo_epochs**中更新的Actor分布 - 考虑了剪裁机制(clip),在**
ppo_epochs次更新中,一旦Actor的更新幅度超过我们的控制范围,则不对它进行参数更新。**
4.2 Critic loss
我们知道,1个batch产出的经验值,不仅被用来更新Actor,还被用来更新Critic。对于Critic loss,不再像Actor loss一样给出一个“演变过程”的解读,直接来看它最后的设计。
首先,在之前的解说中,你可能有这样一个印象:
- $ V_{t} $:Critic对
t时刻的总收益的预估,这个总收益包含即时和未来的概念(预估收益) - $ R_{t} + \gamma * V_{t+1} $:Reward计算出的即时收益 \(R_{t}\) ,Critic预测出的
t+1及之后时候的收益的折现,这是比 \(V_{t}\) 更接近t时刻真值总收益的一个值(实际收益)
所以,我们的第一想法是:\(Critic\_loss =\left(R_{t}+\gamma * V_{t+1}-V_{t}\right)^{2}\)
现在,对“实际收益”和“预估收益”都做一些优化。
(1)实际收益优化
原始的实际收益为 $ R_{t} + \gamma * V_{t+1} $,但是当在actor_loss中引入“优势”的概念时,“优势”中刻画了更为丰富的实时收益信息,所以,将实际收益优化为: \(Adv_{t} + V_{t}\)
(2)预估收益优化
原始的预估收益为 $ V_{t} $。 类比于Actor,Critic模型在ppo_epochs的过程中也是不断更新的。所以这个 \(V_{t}\) 可以理解成是 \(Critic_{old}\) ,也就是真正吃了batch,参与产出经验的那个时候的Critic产出的收益预测结果。
同样想用旧模型去约束新模型,但对于Critic采用的约束策略就比较简单了,直接看代码,从中可以看出,用老 \(V_{t}\) 设计了了一个变动范围,然后用这个变动范围去约束新 \(V_{t}\)
# self.cliprange_value是一个常量
# old_values: 老critic的预测结果
# values:新critic的预测结果
values_clipped = torch.clamp(
values,
old_values - self.cliprange_value,
old_values + self.cliprange_value,
)
那么最终就取实际收益和预估收益的MSE做为loss就好,这里注意,计算实际收益时 \(Adv_{t}\), \(V_{t}\) 都是老Critic(真正吃了batch的那个)产出的结果,而预估收益是随着ppo_epochs而变动的。
代码如下:
def critic_loss_fn(self, values, old_values, returns, mask):
"""
values: 实时critic跑出来的预估预期收益(是变动的,随着ppo epoch迭代而改变)
old_values:老critic跑出来的预估预期收益(是固定值)
returns:实际预期收益
mask:response部分的mask
self.cliprange_value = 0.2
"""
## value loss
# 用旧的value去约束新的value
values_clipped = torch.clamp(
values,
old_values - self.cliprange_value,
old_values + self.cliprange_value,
)
if self.compute_fp32_loss:
values = values.float()
values_clipped = values_clipped.float()
# critic模型的loss定义为(预估预期收益-实际预期收益)**2
vf_loss1 = (values - returns)**2
vf_loss2 = (values_clipped - returns)**2
vf_loss = 0.5 * torch.sum(
torch.max(vf_loss1, vf_loss2) * mask) / mask.sum() # 同样,最后也是把critic loss平均到每个token上
return vf_loss




